Descartes et les Mathématiques

Configurations fondamentales - Seconde

Exercices de géométrie plane avec la géométrie dynamique : puzzle, triangle, point fixe.

Exercices pouvant être résolus avec les configurations fondamentales du plan

Pour les triangles, il s'agit de savoir mettre en œuvre :

  – les propriétés des droites remarquables,

  – la droite des milieux et le théorème de Thalès,

  – les propriétés des angles et des aires des triangles,

  – les propriétés des triangles isocèles et équilatéraux,

  – les propriétés des triangles rectangles et l'inscription dans un demi-cercle.

En seconde, la difficulté des raisonnements vient souvent de l'enchaînement de deux propriétés remarquables.

Montrer que trois droites sont concourantes

Démonstration en deux étapes : trouver le point d'intersection de deux des droites, puis montrer qu'il appartient à la troisième droite.

Droites remarquables du triangle : les trois droites sont des droites remarquables et le point de concours est alors le point remarquable correspondant (centre de gravité, orthocentre…).

Homothétie : Le point de concours est le centre d'une homothétie (maintenant hors des programmes du lycée).

En 1^ère S, montrer que le point de concours est le barycentre de trois paires de points situées sur chacune des droites.

1. Puzzle de Dedeney, du carré au triangle isocèle

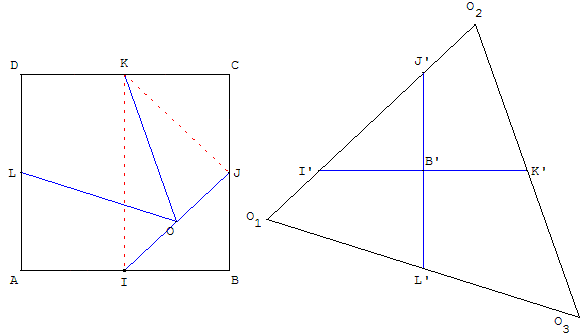
Recomposer les quatre pièces du carré pour obtenir un triangle isocèle.

Les angles à la base ont 2 comme valeur de la tangente : tan(KÔJ) = KJ/OJ = 2.

Télécharger la figure GéoPlan tr_puzzle.g2w

2. Puzzle et carrés : puzzle de Périgal

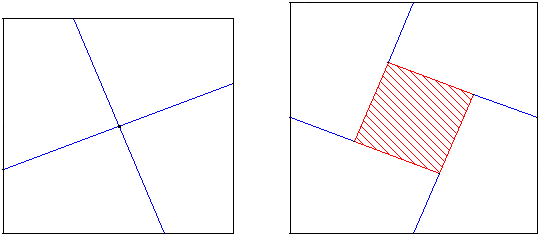
Quatre pièces

Deux droites perpendiculaires, passant par le centre d'un carré, le partagent en quatre quadrilatères égaux.
Avec les mêmes pièces, former deux carrés.

Solution (figure de droite) : le deuxième carré est un trou au centre du grand carré.

Cinq pièces

Avec les quatre quadrilatères et le petit carré central, on obtient un puzzle de cinq pièces qui permet d'obtenir :
  • ou bien le grand carré de droite,
  • ou bien deux petits carrés.

Ce puzzle permet de retrouver le découpage de Périgal, une des démonstrations géométriques du théorème de Pythagore.

Télécharger la figure GéoPlan partage_gateau.g2w

3. Utiliser un orthocentre

3.a. Droites perpendiculaires dans un triangle rectangle

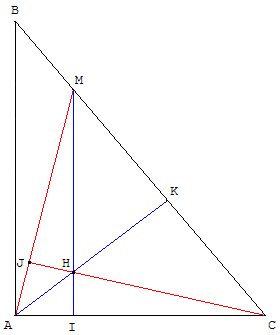
ABC est un triangle rectangle en A, de hauteur (AK).
M est un point variable sur l'hypoténuse [BC].
La parallèle à (AB) passant par M coupe (AK) en H et [AC] en I.

Montrer que la droite (CH) est perpendiculaire à (AM).

Indication

(AK) et (MI) sont deux hauteurs du triangle AMC qui se coupent en H.
H est donc l'orthocentre du triangle AMC. (CH) est la troisième hauteur de ce triangle.
Cette hauteur (CH) est perpendiculaire, en J, au côté [AM].

Télécharger la figure GéoPlan orthocentre.g2w

Voir aussi : deux cercles

3.b. Droites perpendiculaires autour d'un triangle rectangle

ABC est un triangle rectangle en A, et M un point variable de l'hypoténuse.

La droite (d), perpendiculaire à (BC) en M, coupe (AB) en I et (AC) en J.

Montrer que la droite (BJ) est perpendiculaire à (CI).

Indication

Selon la position du point M, J est l'orthocentre du triangle IBC ou bien I est l'orthocentre du triangle JBC.

(BJ) ou (CI) est alors la troisième hauteur du triangle considéré.

Les droites (BJ) et (CI) sont perpendiculaire.

Figure interactive dans GeoGebraTube : droites perpendiculaires autour d'un triangle rectangle

3.c. Droites perpendiculaires autour d'un carré

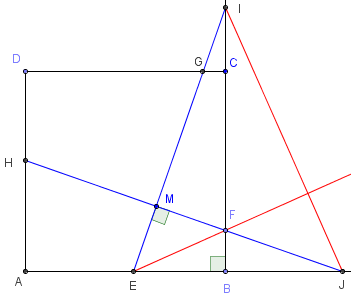
À l'intérieur un carré ABCD, on place un point M et sur le côté [BC], un point F.

La droite (FM) coupe [DA] en H et la demi-droite [AB) en J.
La droite perpendiculaire à (FM) en M coupe les côtés [AB] en E, [CD] en G et la demi-droite [BC) en I.

Lorsque les points E, F, G, H, I et J existent, montrer que les droites (EF) et (IJ) sont perpendiculaires.

Indication

(IB) et (JM) sont deux hauteurs du triangle IEJ qui se coupent en F.
F est donc l'orthocentre du triangle IEJ. (EF) est la troisième hauteur de ce triangle.
Cette hauteur (EF) est perpendiculaire au côté [IJ].

Figure interactive dans GeoGebraTube : droites perpendiculaires dans un carré

4. Reconnaître un orthocentre

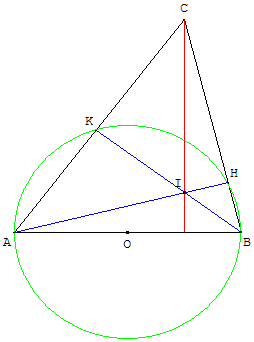
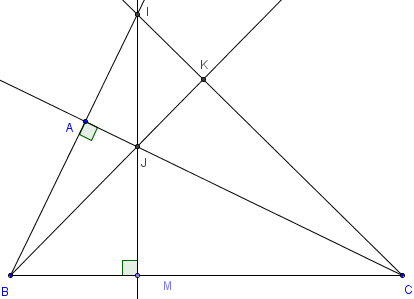
ABC est un triangle.

Le cercle de diamètre [AB] recoupe les côtés [BC] et [AC] en H et K.

Que représente le point I, intersection de (AH) et (BK), pour le triangle ABC ?
Montrer que la droite (CI) est perpendiculaire au côté [AB].

Indication

Les angles AHB et AKB, inscrits dans le demi-cercle de diamètre [AB], sont droits.
Les droites (AH) et (BK) sont deux hauteurs du triangle ABC.
I est donc l'orthocentre du triangle ABC. (CI) est la troisième hauteur de ce triangle.
Cette hauteur (CI) est perpendiculaire au côté [AB].

Télécharger la figure GéoPlan hauteurs.g2w

5. Point fixe

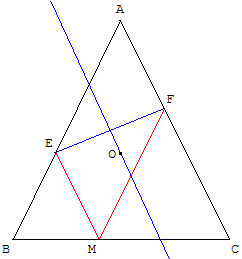
Hors programme

ABC est un triangle isocèle en A.
M est un point variable sur [BC].

La parallèle à (AC) passant par M coupe le côté [AB] en E et la parallèle à (AB) passant par M coupe le côté [AC] en F.

Montrer que la médiatrice (d) de [EF] pivote autour d'un point fixe lorsque M décrit le segment [BC].

Télécharger la figure GéoPlan point_fixe.g2w

Démonstration avec une rotation

Soit O le centre du cercle circonscrit à ABC, point de concours des médiatrices.

La rotation de centre O et d'angle (, ) transforme A en B, C en A et donc F en E puisque AF = EM = BE.
Par suite, OE = OF et O appartient à la médiatrice (d) de [EF].