 Descartes et les Mathématiques
Descartes et les Mathématiques
Parallélogrammes en seconde
Configurations du plan :
parallélogrammes, rectangles, parallélogrammes avec contraintes.
Sommaire
3. D'un parallélogramme à l'autre
4. Parallélogramme et bissectrice
5. Comparaison d'aires dans un rectangle
6. Parallélogramme avec contraintes
Construire un parallélogramme dont deux sommets sont situés sur deux droites
Propriétés
Voir : parallélogrammes au collège
1. Thalès et parallélogramme
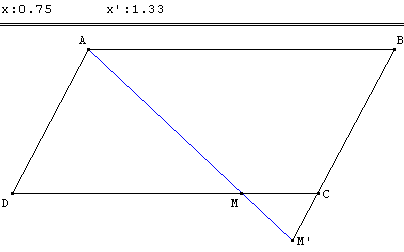
ABCD est un parallélogramme.
M est un point sur la droite (DC) tel que ![]() = x
= x ![]() .
.
M’ est le point de la droite (BC) tel que ![]() =
=
![]()
![]() .
.
Montrer que les points A, M et M’ sont alignés.
Google préfère la mauvaise copie d'HauEtFort à cette figure originale !
2. Projections orthogonales des sommets
sur les diagonales
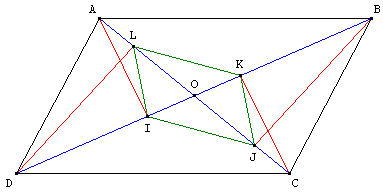
ABCD est un
parallélogramme.
I, J, K, L sont
les projections
orthogonales des
sommets
sur les diagonales.
Montrer que
IJKL est un
parallélogramme.
3. D'un parallélogramme à l'autre
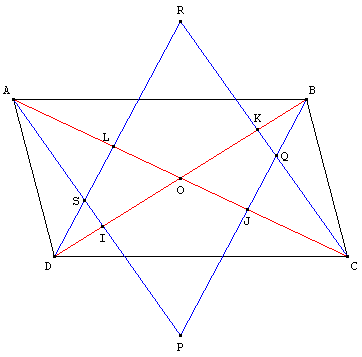
Les points P, Q, R et S sont les points d'intersection des
droites perpendiculaires aux diagonales issues des sommets.
Montrer que PQRS est un parallélogramme.
Lorsque ABCD est un rectangle, montrer que PQRS est alors un losange.
Google préfère la mauvaise copie d'HauEtFort à cette image originale !
4. Parallélogramme et bissectrices
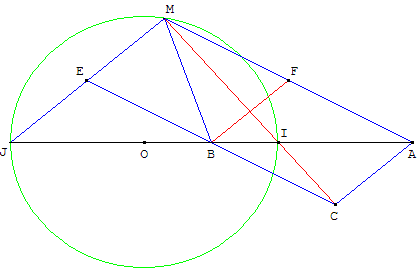
Résoudre par une méthode géométrique, dans R,
l'équation 2 |x - 1| - |x - 4| = 0.
AMEC est un parallélogramme. Une droite (d) passant par A
coupe les segments [MC] et [CE] respectivement en I et B,
et intercepte la droite (ME) en J.
Sachant que AI = 2 et IB =1, calculer la longueur BJ.
Comme (AM) est parallèle à (BC), les triangles IAM et IBC
sont semblables et de rapport de similitude ![]() .
.
Donc, BC = ![]() AM =
AM = ![]() CE et B est le milieu de [EC].
CE et B est le milieu de [EC].
Dans le triangle JAM, EB = ![]() AM, la droite (BE)
AM, la droite (BE)
parallèle à (AM) est une droite des milieux :
B est le milieu de [AJ] et E le milieu de [MJ].
On admettra que les droites (MJ) et (MC) sont perpendiculaires.
Si F est le milieu de [MA], (BF), joignant les milieux des côtés
du parallélogramme AMEC, est parallèle à (ME) ;
donc perpendiculaire à (MC).
(MC) diagonale du parallélogramme est une médiane du triangle
MBF, elle est aussi une médiatrice, d'où MBF admettant (MC)
comme axe de symétrie est un triangle isocèle et MB = MF = ![]() MA
MA
Comme MA = 2 MB, M est sur (c), cercle d'Apollonius de
diamètre [IJ], ensemble des points M tels que ![]() = 2.
= 2.
Si M est distinct de I et J, les droites (MI) et (MJ) sont les
bissectrices intérieure et extérieure de l'angle AMB.
Sur la droite (d) choisissons le repère (O, B) d'origine O milieu
de [IJ]. On a alors les abscisses B(1) et A(4).
Un point M de la droite d'abscisse x est tel que MB = |x - 1| et MA = |x - 4|.
L'intersection du cercle (c) et de la droite (d) est l'ensemble
des points de la droite vérifiant ![]() = 2.
= 2.
C'est l'ensemble des points {I, J} dont les abscisses vérifient
l'équation 2 |x - 1| - |x - 4| = 0,
soit x = 2 ou x = −2.
D'où les points d'abscisses I(2) et J(-2).
5. Comparaison d'aires dans un rectangle
Comparaison d'aires sans calcul :
L@ feuille à problèmes
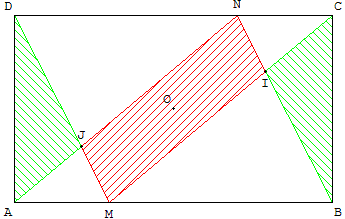
ABCD est un rectangle
de centre O.
Sur [AB] et [CD] placer
deux points M et N,
tels que AM = CN.
Les deux triangles verts
ont la même aire.
L'aire du parallélogramme
rouge est égale à celle
des deux triangles.
Indications pour la solution
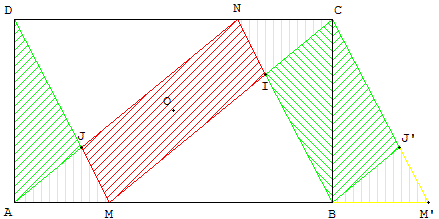
C est l'image de A dans la symétrie de centre O. ![]() = −
= − ![]() :
:
les points M et N sont symétriques par rapport à O.
Par la symétrie de centre O, la droite (AN) a pour image (CM),
(DM) a pour image (BN). Les points d'intersection I et J sont
donc symétriques par rapport à O et MINJ est un parallélogramme.
Le triangle CBI est symétrique du triangle ADJ : ils ont même aire.
La translation de vecteur ![]() transforme M en M’,
transforme M en M’,
J en J’et le triangle ADJ en BCJ’.
Ces deux triangles ont même aire.
Par composition de la symétrie et de la translation, on montre
que BJ’CI est un parallélogramme, d'aire égale à celle des deux triangles.
Par symétries ou translation, les triangles en jaune sont d'aires égales.
Les parallélogrammes NCMA et NCM’B ont
même aire égale NC × CB.
En enlevant les triangles jaunes, on « voit» que
les parallélogrammes MINJ et BJ’CI ont même aire.
L'aire du parallélogramme MINJ est égale à celle
des deux triangles CBJ’ et DBI, donc celles de ADJ et DBI.
6. Parallélogramme avec contraintes
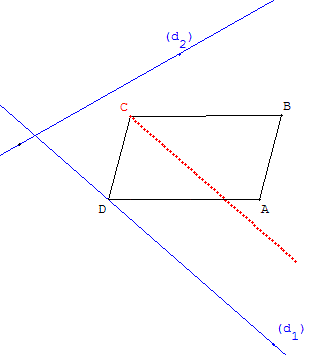
Construire un parallélogramme dont deux
sommets sont situés sur deux droites
On donne deux points A, B distincts et deux
droites (d1), (d2) sécantes, et distinctes de (AB).
Existe-t-il un point C sur (d2) et un point D sur (d1)
tel que le quadrilatère ABCD soit un parallélogramme ?
Analyse
Placer un point D variable sur (d1) et tracer le
quatrième point C du parallélogramme ABCD.
Déplacer le point D jusqu'à ce que C soit sur la droite (d2).
Solution
Parallélogramme avec 2 sommets sont situés sur 2 droites
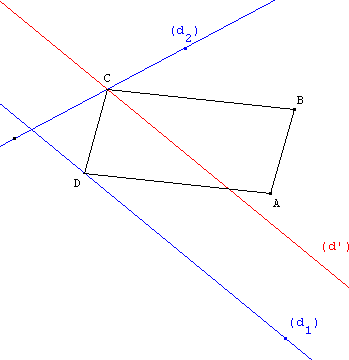
La trace du lieu du point C permet de réaliser que ce
point est situé sur une droite parallèle à (d1).
Il suffit donc de tracer la droite (d’), image de (d1)
par la translation de vecteur ![]() . Les droites (d2) et (d’) sont sécantes en C.
. Les droites (d2) et (d’) sont sécantes en C.
Le point D, image de C par la translation réciproque
de vecteur ![]() , est situé sur (d1)
et
, est situé sur (d1)
et ![]() =
= ![]() :
:
le parallélogramme ABCD est la solution du problème.
Table des matières
La translation dans d'autres pages du site
Alignement – Translation et orthocentre
Dans d'autres pages du site
Liens pour la géométrie au collège
Parallélogrammes au collège
Taille d'une bille inscrite dans un rectangle
Bissectrices d'un parallélogramme
Lycée
Barycentres et parallélogrammes
Point aligné sur une diagonale : parallélogramme de Pappus
![]() Mobile friendly ; sur ordinateur, version desktop
Mobile friendly ; sur ordinateur, version desktop
Copyright 2004 - © Patrice Debart
|
|
Page no 64, réalisée le 22/2/2004 |