Descartes et les Mathématiques
La trisection de l'angle
Le troisième grand problème de la géométrie grecque
Sommaire
Utilisation de fonctions en géométrie
2. La quadratrice de Dinostrate
4. Conchoïde de droite
Géométrie synthétique
10. Trisection d'un angle droit
13. Trisection par les compagnons du Moyen-Âge
Partager un angle quelconque en trois angles égaux.
La trisection est un des trois grands problèmes de l'Antiquité, avec la quadrature du cercle et la duplication du cube.
À l'aide d'une règle et d'un compas, ce problème, comme les deux autres, n'a pas de solution. Pierre-Laurent Wantzel l'a démontré en 1837.
1. Trisection de l'angle
Pour la trisection d'un angle θ, il faut trouver t tel que 3t = θ, d'où cos 3t = cos θ.
Avec la formule cos 3t = 4 cos3t − 3 cos t, en posant
cos t = x,
x est une solution de l'équation 4 x3 − 3 x = cos θ.
La trisection revient à savoir si les solutions de cette équation sont constructibles.
D'après le théorème de Wantzel, pour que la trisection soit possible, l'équation :
4 x3 − 3 x − cos θ = 0 doit être réductible au second degré dans Q.
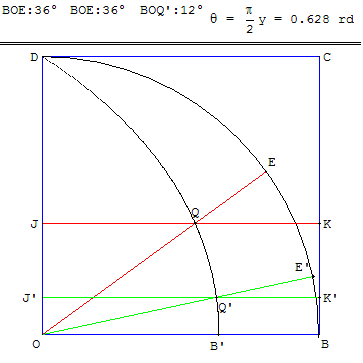
Trisection de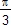 
Par exemple, la trisection d'un angle de mesure θ = n'est pas possible :
cos(
), solution de l'équation 4 x3 − 3 x − 
= 0 irréductible dans Q[X], est algébrique sur Q de degré 3.
Ce qui montre, du même coup, l'impossibilité de construire à la « règle et au compas » l'ennéagone régulier (9 côtés), résultat prouvé en 1801 par Gauss.
Indication
Soit 
une solution rationnelle irréductible de l'équation 8 x3 − 6 x − 1 = 0.
Il s'ensuit, dans Z, l'égalité : 8p3 − 6pq2 − q3 = 0
Il résulte du théorème de Gauss que p divise − 1 et q divise 8. Les candidats pour sont à chercher parmi les facteurs de 
.
Dans ce cas particulier, de l'égalité : 8p3 − 6pq2 = q3, on trouve que q est pair.
Posons q = 2r. Il vient p3 − 3 pr2 = r3. Soit p(p2 − 3 r2) = r3, donc p divise r3 et comme p3 = r(3pr + r2) on a r divise p3.
Mais la fraction étant irréductible p est premier avec q et par suite avec sa moitié r. Donc p = ±1 et r = ± 1, d'où q = ± 2.
En conséquence x = ± et on vérifie que ± n'est pas solution de l'équation.
Polynôme minimal du troisième degré
P(x) = 8 x3 − 6 x − 1 admet comme solution cos(). Cette solution n'est pas rationnelle.
Soit un autre polynôme Q(x) de Q[X], de degré moindre, qui aurait cos() comme 0.
Si Q(x) était un binôme de degré 1, il admettrait une solution rationnelle ce qui n'est pas le cas.
Q(x) est donc du second degré. Grâce à la division euclidienne de P(x) par Q(x), on trouve P(x) = Q(x) (ax + b) + R(x), avec a non nul et R(x) binôme du premier degré.
En remplaçant x par cos(), on trouve que R(cos()) = 0, cette solution n'étant pas rationnelle, cette première contradiction impose donc R(x) = 0.
P(x) alors égal à Q(x) (ax + b) serait factorisable dans Q[X] et aurait − b/a pour solution ce qui est impossible.
cos() n'est pas solution d'une équation du second degré à coefficients entiers. P(x) est irréductible dans Q[X].
cos() est algébrique sur Q de degré 3 et le nombre cos() n'est pas constructible.
Voir aussi une démonstration montrant si l'équation admet une solution constructive, elle admet une solution rationnelle, d'où la contradiction.
Utilisation de fonctions en géométrie
2. La quadratrice de Dinostrate
(ou quadratrice d'Hippias)
Hippias d'Élis, philosophe sophiste grec, contemporain de Socrate né vers 460 avant J.-C., cherchant à résoudre le problème de la trisection de l'angle, inventa une courbe trisectrice permettant une solution approchée.
Le problème étant insoluble, la courbe permet de trouver des solutions approchées.
La trisectrice est appelée plutôt la quadratrice de Dinostrate, car ce dernier l'utilisa pour résoudre la quadrature du cercle.
Le point K se déplace uniformément sur le segment [BC],
son ordonnée est y, avec 0 ≤ y ≤ 1,
le point E se déplace uniformément sur le quart de cercle BD, l'angle BÔE mesure 90y degrés, soit θ = 
y radians.
La droite horizontale (JK) coupe la droite (OE) en Q. La courbe décrite par Q est la quadratrice de Dionostrate.
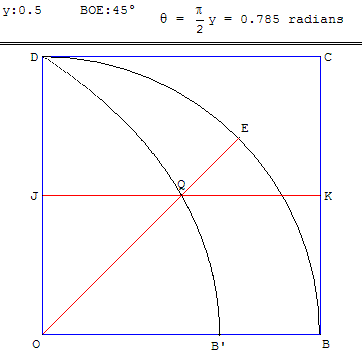
Soit OK’ = OK/3 et OJ’ = OJ/3 correspondant à y/3. La droite horizontale (J’K’) coupe la quadratrice en Q’. La droite (OQ’) est alors une trisectrice de l'angle BÔE.
Télécharger les figures GéoPlan dinostrate.g2w, dinostrate_tri.g2w
Figure exportée dans : mécanique hyperbolique algébrique
3. Quadrature du cercle
Dans le triangle OJQ rectangle en J, d'angle aigu OQJ = BOE = θ,
on a y = OJ = OQ sin θ.
Avec OQ = ρ, comme θ = y, on a θ = ρ sin θ.
L'équation polaire de la quadratrice est ρ = 
.
Le point B’ d'intersection de la quadratrice avec [OB] a pour abscisse 
. Ce point, non constructible, est obtenu avec une approximation théorique aussi grande que l'on veut.
Viète (1540-1603) calculera le premier produit infini des mathématiques :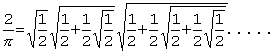 
( formule de Viète)
4. Conchoïde de droite
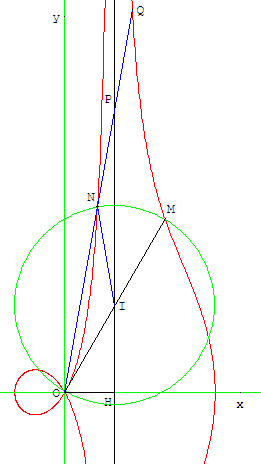
Avec la conchoïde, Nicomède, mathématicien grec du IIe siècle avant J.-C., fut le premier à réaliser une construction mécanique d'une courbe plane (autre que le cercle).
Étant donné une directrice (d), un pôle O non situé sur (d), et un module b,
à partir d'un point P de la directrice, on construit les deux points N et Q de la droite (OP) situés à une distance b de P tels que :
PN = PQ = b.
La conchoïde est le lieu géométrique des points N et Q, lorsque P parcourt (d).
C'est la courbe d'équation polaire ρ = 
+ b, où a est la distance du pôle à la directrice (a = OH).
Les conchoïdes de Nicomède sont des trisectrices
Pour cela, construire un triangle OHI rectangle en H, tel que l'angle φ à trisecter soit OÎH.
Construire la conchoïde de la droite (IH) de pôle O et,
de module b = OI = 
, où a = OH.
Pour un angle φ, la conchoïde a pour équation ρ = + .
À chaque angle à trisecter, correspond une conchoïde différente.
L'intersection de la courbe avec le cercle de centre I, passant par O, permet de déterminer deux points M et N, et grâce aux propriétés fondamentales de la conchoïde, on montre que l'angle NÎP trisecte l'angle OÎH.
Pour le point I, situé sur la directrice, les deux points de la conchoïde situés sur la droite (OI), à une distance b de I sont le point O et un point M symétrique de O par rapport à I.
Le cercle de centre I et de rayon OI passe par le pôle O, coupe la conchoïde en M.
Ce cercle coupe la conchoïde en un troisième point N dont la construction est approchée :
la droite (ON) coupe la directrice en P tel que NP = b.
On retrouve la configuration de Viète, deux triangles isocèles de côtés égaux à b, d'angles α et 2α :
− L'angle trisecté est OPH, car le triangle INP est isocèle avec OPH = NIP = α ;
− les angles aigus du triangle isocèle ION sont égaux à 2α ;
− les angles alternes-internes yOP et OPH sont égaux à α ;
− les angles alternes-internes yOI et OIH sont égaux à 3α et φ = 3α.
L'angle NÎP est le tiers de l'angle OÎH.
Télécharger la figure GéoPlan conchoide.g2w
Descartes : les coordonnées cartésiennes
Article exporté dans WikiPédia : Conchoïde
Image exportée dans WikiPédia : Trisection de l'angle
5. Hyperbole de Chasles
Extrait de l'article de Jean-Pierre Friedelmeyer :
Une trisection de l'angle ou Michel Chasles revisité où l'on trouvera tous les calculs.
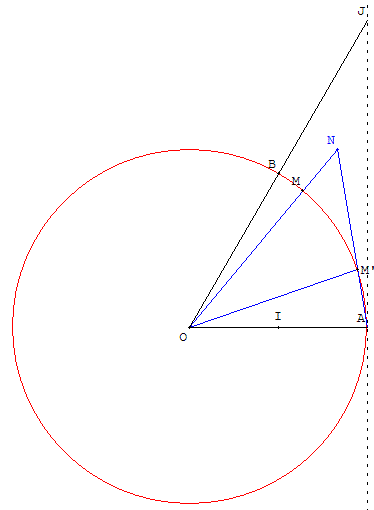
Énoncé
Étant donné deux points A et B du cercle trigonométrique (c) de centre O,
on cherche les points M de (c) tels que :
(
, 
) = 3(
, ),
ou encore tel que (, ) = 2(, ).
Méthode de résolution
À tout point M de (c), on fait correspondre le point M’ de (c) tel que
(, ’) = 2(, ).
La ou les solutions du problème sont données par les points M tels que M = M’.
Traçons les droites (OM) et (AM’) et notons N le point d'intersection de ces deux droites.
On remarque que le point N coïncide avec M si et seulement si M = M’ ; à condition d'exclure le cas où M est en B et M’ en A car, alors, la droite (AM’) n'est pas définie.
• On est donc conduit à chercher le lieu (H) du point N,
• et à déterminer les points d'intersection de (H) et (c).
Résolution du problème
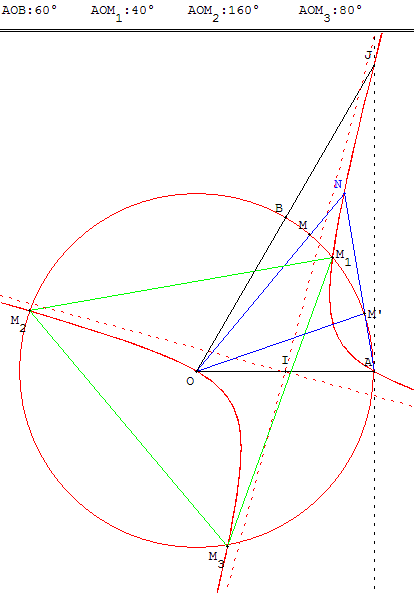
Comme le disait Chasles « On reconnaît sans difficulté que la conique, lieu du point N, est une hyperbole équilatère… » dont le centre est le milieu I de [OA].
Les axes de l'hyperbole sont parallèles aux bissectrices de l'angle (OA, OB).
Soit le point J d'intersection de (OB) avec la tangente en A au cercle.
Les asymptotes sont parallèles aux bissectrices de l'angle (JO, JA).
Elles sont aussi parallèles aux bissectrices de l'angle (NO, NA).
Soit α = (, ) ; φ = α/2 − π/4 ;
u = cos(φ) ; v = sin(φ) ;
U point de coordonnées (u, v) et V(−v, u).
Dans le repère (O, 
, 
) l'hyperbole a pour équation :
y = vx/(u − 2x).
Il y a trois solutions, les sommets d'un triangle équilatéral inscrit dans le cercle.
Télécharger la figure GéoPlan trisect_chasle.g2w
Géométrie synthétique
6. Méthode de Viète
De la classe de quatrième à la classe de seconde
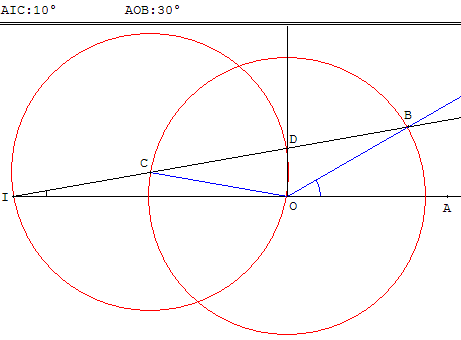
Triple d'un angle
On prend un angle AIC que l'on souhaite tripler.
À partir du point C on trace le cercle de rayon IC qui coupe [IA) en O et [IC) en D.
Le cercle de centre O et de rayon OC coupe [IC) en B
et on a AOB = 3 AIC.
On retrouve cette configuration dans les diverses figures de cette page.
Télécharger la figure GéoPlan triple_angle.g2w
Trisection
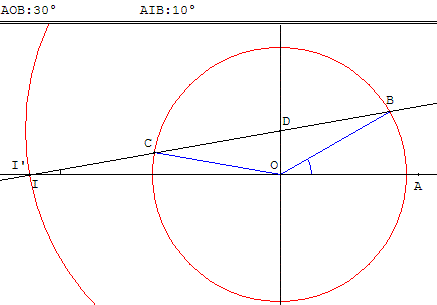
Réciproquement : reprendre la construction précédente à l'envers, en construisant le cercle de centre O, de rayon OB, ainsi que la perpendiculaire à (OA) passant par O.
Un point variable D est sur cette perpendiculaire et le point I est à l'intersection de (CD) et (OA).
Par ailleurs, on a DI = 2OB, à partir de D on construit le cercle de centre D de rayon 2OB,
qui coupe (OA) en I’.
Déplacer le point D, lorsque I et I’ sont confondus,
on a évidemment AIB = 
AOB.
Télécharger la figure GéoPlan trisect_viete.g2w
Remarque : Le point I n'est pas constructible à la « règle et au compas », GéoPlan ne peut pas le placer géométriquement.
7. Méthode d'Archimède
3e siècle avant Jésus-Christ
On attribué à Archimède cette construction par ajustement (inclinaison ou neusis).
À l'aide d'un compas et d'une règle portant deux graduations, ou avec GéoPlan, cette construction est exacte.
Sur un cercle de centre O, on place deux points A et B et on nomme 3α l'angle AÔB.
Soit C le point diamétralement opposé à A.
Placer sur le cercle le point D tel que la droite (BD) coupe (AC) en E de telle sorte que ED est égal au rayon du cercle.
Construction par neusis
C'est une technique de construction géométrique qui consiste à placer un segment ED de longueur fixée {OD} entre deux lignes {(OA) et (c)}, en le faisant passer par un point fixe B.
Pour cela, placer deux points D et E sur une règle, tels que DE = OA.
Faire glisser la règle de telle sorte qu'elle passe le point B et que le point E se déplace sur la droite (OA).
On s'arrête lorsque le point D de la règle tombe exactement sur le cercle.
Montrer que l'angle AEB est égal au tiers de l'angle AÔB : AEB = α.
Télécharger la figure GéoPlan trisect_archimede.g2w
Démonstration : les triangles OBD et DEO sont isocèles, on a donc les angles égaux :
DBO = BDO et DOE = DEO = α.
L'angle extérieur ODB du triangle DOE est égal à la somme des deux angles intérieurs non adjacents OED et DOE,
donc l'angle ODB et la somme OED + DOE = 2 OED = 2α sont deux façons d'exprimer l'angle supplémentaire de EDO.
Or AOB + DOE = AOB + α et ODB + OBD = 2α + 2α sont deux façons d'exprimer l'angle supplémentaire de BOD, soit AOB + α = 4 α,
en simplifiant AOB = 3 α.
Remarque : cette méthode de « coïncidence de points » n'est pas une construction « à la règle et au compas ».
Les points D et E sont deux points d'une règle graduée et ne sont pas constructibles ; GéoPlan ne peut pas les placer géométriquement.
Avec GéoPlan, on déplacera le point D avec la souris ou les flèches du clavier pour obtenir un point E sur (AC) : abscisse 0 lorsque (AC) est horizontale.
N'étant pas à une contradiction près, en supposant le problème résolu, avec GéoPlan taper S pour placer les points D et E exactement dans la figure.
Remarque didactique : certains collègues sont contre le fait d'admettre que les élèves, qui déplacent un point sur l'écran, puissent obtenir un résultat avec pour seul moyen de contrôle la perception visuelle.
Heureusement avec GéoPlan, l'affection directe d'un point libre permet d'obtenir une justification analytique (dans mes exemples, j'utilise alors la touche S comme commande).
Un conflit en didactique à propos de différentes médiations sémiotiques dans l'enseignement de la géométrie :
Depuis les journées de rentrée 2008 de l'IREM de Basse-Normandie, nous avons eu l'opportunité de présenter la séquence et les propos de la discussion précédente à d'autres collègues.
Au cours des journées de l'INRP de Lyon qui avaient pour sujet « redonner du sens aux mathématiques enseignées dans le secondaire », nous avons échangé nos points de vue sur le sujet avec l'inspecteur de mathématiques et avec quelques collègues chercheurs en didactique. Ceux-ci nous ont indiqué qu'à leur avis, cette utilisation didactique des logiciels, où les élèves du collège utilisent une configuration de base qui se conserve, était tout à fait dans l'esprit pédagogique des TICE dans l'enseignement à ce niveau de la quatrième.
Dans l'IUFM de Basse-Normandie, notre collègue formateur Olivier Frémont qui est à l'origine des nombreuses ressources TICE pour l'enseignement des mathématiques estime que, sûrement, la non-acceptation au niveau de la quatrième de la démarche des élèves est due à une méconnaissance de cette exploitation pédagogique du logiciel. Dans une partie de la procédure, les élèves utilisent l'invariance d'une configuration, et même si le fait qu'un point soit superposé à un autre est justifié seulement par la perception visuelle, ceci n'est pas très grave dans ce niveau du collège.
Dr. Ruben Rodriguez Herrera
8. Méthode de Pappus
Remarque : cette méthode de « coïncidence de points » n'est pas une construction « à la règle et au compas ».
Créer la droite (d) parallèle à (OB) passant par B et la droite (d’) perpendiculaire à (OA) passant par B, puis le point d'intersection H des 2 droites.
Créer un point variable P sur la droite (d), puis la droite (OP).
Le cercle de centre P et de rayon 2OC coupe le segment [OP] en M.
Créer le point N milieu de [PM], puis le segment [BN].
Déplacer le point P pour que M soit sur (d’).
Les triangles OHM et MBP sont semblables et AOM = BPM.
Si M est sur (d’), les points P, M et B sont sur un même cercle de centre N et de rayon OB. L'angle BNM = 2 BPM.
Le triangle ONB est isocèle et l'angle en MOB = BNM = 2BPM = 2 AOP, d'où AOB = 3 AOM.
Télécharger la figure GéoPlan trisect_pappus.g2w
9. Pliage d'une feuille
Classe de seconde
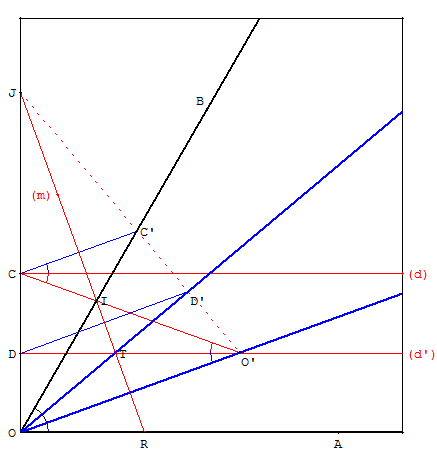
L'origami est une technique plus puissante que « la règle et le compas » et le formalisme du pliage d'une feuille de papier permet ici de réaliser un pli en amenant simultanément un point C donné sur une droite (Δ) et un point O sur une droite (d’).
La trisection de l'angle est alors réalisable, en pliant une feuille de papier, par une construction due à Hisashi Abe (1980), qu'illustre la figure ci-contre :
On trace l'angle AOB à couper en trois en plaçant le sommet O au coin de la feuille de sorte le bord inférieur soit un des côtés de l'angle.
Deux bandes horizontales, de même largeur (arbitraire), sont tracées en bas de la feuille (ceci peut se faire facilement par pliage). On appelle (d) et (d’) les nouvelles droites qui les délimitent.
Il faut maintenant plier la feuille le long d'un pli (m) de sorte que le coin O se trouve déplacé sur la droite (d’) (en un point O’), en même temps que le point C (intersection du bord gauche avec la droite d) se trouve déplacé sur la droite (OB) en un point C’.
La demi-droite, d'origine O, passant par O’ est alors une trisectrice de l'angle donné : l'angle AOO’ vaut de l'angle AOB.
Le point D (intersection du bord gauche avec la droite d’) se trouve déplacé sur la droite (JO’) en un point D’. La demi-droite, d'origine O, passant par D’ est l'autre trisectrice.
Télécharger la figure GéoPlan trisect_abe.g2w
Remarque
Cet exercice montre que les tracés réalisés par pliage, en n'utilisant que des symétries axiales, peuvent aboutir à des figures non constructibles à la « règle et au compas ».
Indications
Trisectrice (OO’)
Si α = AOO’, comme angles alternes-internes α est l'angle de (d’) et (OO’),
par symétrie par rapport à (d’), l'angle de (d’) et (OO’) est égal à l'angle de (d’) et (CO’), angles égaux à α.
Les droites (OC’) et (O’C), symétriques par rapport à la droite (m) se coupent en I situé sur l'axe de symétrie.
Le triangle IOO’, ayant (m) comme axe de symétrie, est isocèle et O’OI = IO’O = 2α.
AOB est bien égal à 3α, (OO’) est une trisectrice.
Trisectrice (OD’)
La symétrie d'axe (m) transforme les points équidistants O, D, C en O’, D’, C’. Le point D’ est donc le milieu de O’C’. La droite (OD’) est la médiane du triangle OO’C’.
Cette symétrie d'axe (m) transforme l'angle droit ODO’ en O’D’O. (OD’), perpendiculaire à (O’D’), est une hauteur du triangle OO’C’.
(OD’), médiane et hauteur du triangle OO’C’, est une médiatrice. OO’C’ est un triangle isocèle et (OD’) en est une bissectrice.
Comme vu ci-dessus O’OC’ = 2α, on a donc AOO’ = O’OD’ = D’OB = α. On a bien le partage de AOB en trois angles égaux.
10. Trisection d'un angle droit !
Construction triviale au compas seul.
Félix Klein - Problèmes célèbres de la géométrie élémentaire
Le tracé de trois cercles de même rayon permet de trouver les trisectrices (OC) et (OD) de l'angle droit AÔB.
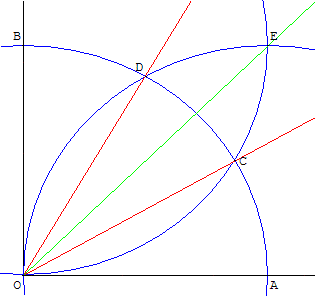
Le double ou la moitié d'un angle trisectable est trisectable :
(OE) est la bissectrice de AÔB. AÔE est un angle de 
,
(OC) est une des trisectrices de cet angle,
l'autre trisectrice est la bissectrice de AÔC.
On peut continuer avec la bissectrice de AÔE pour trouver, avec le compas, les trisectrices d'un angle de 
,
et ainsi de suite les angles de la forme 
sont trisectables.
cos et sin sont donc constructibles.
Voir calculs : angles trigonométrie
Télécharger la figure GéoPlan trisec_droit.g2w
11. Autre trisection d'un angle droit !
Une construction à la règle au compas.
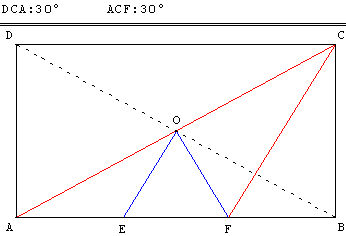
E et F partagent un segment [AB], de longueur 3, en trois unités.
Le point O complète le triangle équilatéral EFO.
C et D sont les deux autres sommets du rectangle ABCD de centre O.
Montrer que les droites (CA) et (CF) sont les trisectrices de l'angle DCB.
AB = BC = 3 et BC = AD = 
.
Vérifier que tan(DCA) et tan(FCB) sont égaux à 
.
Télécharger la figure GéoPlan trisect.g2w
Google préfère la copie d'HauEtFort à cette figure originale !
Construction des deux trisectrices
Sur un des côtés d'un angle droit de sommet C, placer le point B tel que CB = et sur la perpendiculaire à (BC) placer le point F tel que FB =1
(le triangle rectangle FBC est un demi-triangle équilatéral).
Sur la demi-droite [BF) placer le point A tel que AB = 3.
(CF) et (CA) trisectent l'angle droit BCD (où D est le quatrième sommet du rectangle ABC…)
12. Équerres trisectrices
Il est possible d'approcher le partage d'un angle en trois avec une équerre en forme de L de largeur l.
Sur le pied de l'équerre, on place les points équidistants A, B et C tels que AB = BC = l.
Équerre en L de Carpenter
Pour la trisection approchée de l'angle xOy tracer la parallèle à (Ox) située à la distance l.
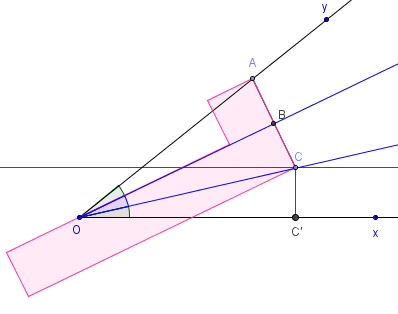
On déplace l'équerre en plaçant le coin A sur (Oy) et le sommet O sur le bord médian de l'équerre, de telle manière que C soit sur la parallèle.
Les droites (OB) et (OC) partagent l'angle en 3.
Si C’ est la projection de C sur (Ox), les triangles rectangles OAB, OBC et OCC’ sont isométriques et par suite les angles AOB, BOC et COx sont de même mesure.
Commande GeoGebra : déplacer le point A pour trouver la solution lorsque C est sur la parallèle.
Figure interactive dans GeoGebraTube : trisection avec une équerre en L
Équerre de Bergery et Grisel
La projection C’ de C sur (Ox), est située sur le cercle de centre C, passant par B.
D'où l'aménagement de l'équerre en y ajoutant ce demi-cercle de centre C.
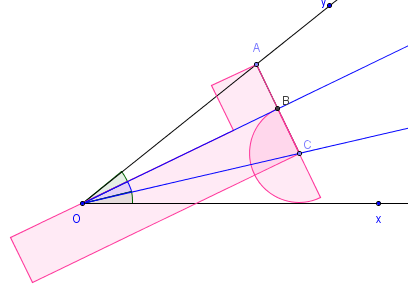
On déplace alors l'équerre en plaçant le coin A sur (Oy) et le sommet O sur le bord médian de l'équerre, de telle manière que l'arc de cercle soit tangent à (Ox).
Commande GeoGebra : déplacer le point A pour trouver la tangence.
Figure interactive dans GeoGebraTube : trisection avec une équerre de Grisel
Références : Le petit Archimède no 49
Grisel : Sur la trisection de l'angle
Jean Aymès : la trisection de l'angle, ancienne brochure APMEP
Henry Plane : Plot no 34
13. Trisection des compagnons bâtisseurs
Soit un angle AOB, avec les points A et B sur un cercle (c) de centre O.
C est le point diamétralement opposé à B.
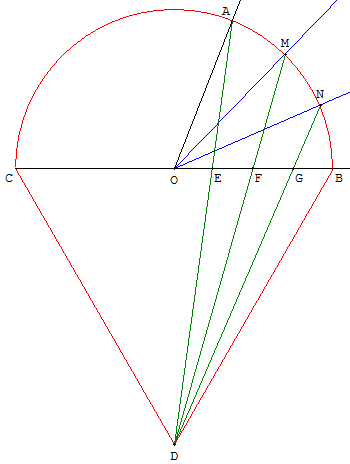
Tracer le cercle de centre C passant par B, ainsi que le cercle de centre B passant par C.
Le point D est un des points d'intersection de ces deux cercles, tel que le triangle équilatéral BCD et le demi-cercle (c) soient de part et d'autre de (BC).
La droite (AD) coupe [BC] en E.
Les points F et G divisent le segment [EB] en trois parts égales.
Les droites (DF) et (DG) coupent le demi-cercle (c) en M et N.
Les angles AOM, MON et NOB sont sensiblement égaux.
L'angle donné AOB se trouve ainsi approximativement divisé en trois.
Télécharger la figure GéoPlan Trisect_batisseur.g2w
Retrouver cette figure pour la trisection exacte du demi-cercle par les compagnons bâtisseurs du Moyen-Âge
14. Application : théorème de Morley
Les points d'intersection des trisectrices des angles d'un triangle forment un triangle équilatéral, le « triangle de Morley » du triangle initial.
Table des matières
Les Éléments d'Euclide
Dans d'autres pages du site
Cercles d'Apollonius
, π : petits programmes TI-92
Google friendly
Copyright 2005 - © Patrice Debart
Rétroliens (backlinks)
Les trois problèmes de l'antiquité : m@ths et tiques
Quadratrice publié par Sylvain Tremblay
|
|
Page no 194, déplacée le 2/8/2013 |