Dans un triangle non équilatéral, l'orthocentre, le centre de gravité et le centre du cercle circonscrit sont distincts et alignés. La droite passant par ces trois points est la droite d'Euler.

1.a. Exemple de vrai problème posé par Daniel Perrin :

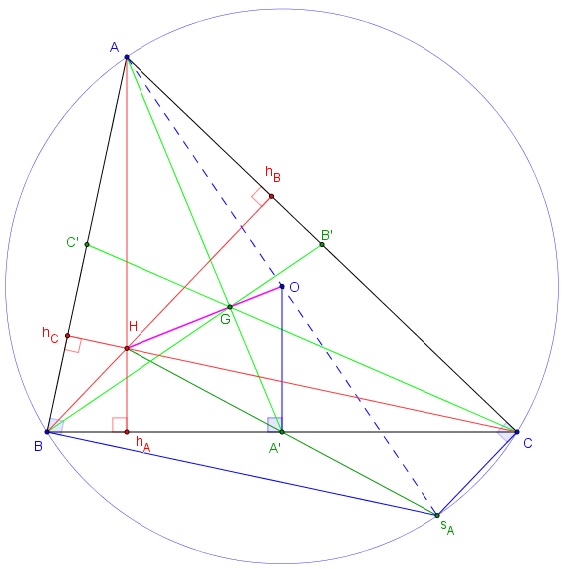
O est le centre du cercle circonscrit au triangle ABC, H est l'orthocentre du triangle et G le centre de gravité.
s_A est diamétralement opposé à A.

Montrer ce l'on voit sur la figure.

Figure interactive dans GeoGebraTube : droite d'Euler

Exemple de formulation, style problème de bac
Exercice trop simple, trop saucissonné. À chaque question, une seule chose à vérifier. Les élèves ne peuvent que donner la bonne réponse, avec les canons de rédaction attendus :

(BH) est perpendiculaire à (AC) et (CH) à (AB).
Montrer que le triangle As_AC est rectangle en C. En déduire que (s_AC) est parallèle à (BH).
Montrer que le quadrilatère BHCs_A est un parallélogramme.
Montrer le point d’intersection A’ de (BC) et (Hs_A) est le milieu de [BC] et de [Hs_A].
Montrer que G est sur (AA’), au tiers de [AA’] à partir de A’ et en déduire que G est aussi le centre de gravité de AHs_A.
Montrer que G est sur (HO), au tiers de [HO] à partir de O.

Avec un tel texte, l'élève devient une sorte d'OS de la géométrie qui n'a plus que des tâches parcellaires à accomplir, sans avoir le contrôle de la stratégie globale.

1.b. Relation d'Euler dans le triangle

Dans un triangle équilatéral, le centre du cercle circonscrit, le centre de gravité et l'orthocentre sont confondus.
Sinon, soit ABC un triangle non équilatéral, O le centre du cercle circonscrit, G le centre de gravité et H l'orthocentre.

Pour démontrer l'égalité vectorielle = + + (relation d'Euler), faire un changement de point de vue
en transformant l'exercice en « caractériser le point M tel que = + + ».

Caractérisation vectorielle de l'orthocentre

geometrie du triangle - droite d'euler - copyright Patrice Debart 2002

Soit M le point tel que : = + + ,
d'où – = + .

Une relation de Chasles permet d'écrire : = +
et si A’ est le milieu de [BC], la forme vectorielle du théorème de la médiane
donne + = 2,
d'où = 2 .

Le vecteur est colinéaire à . C'est un vecteur directeur de la médiatrice de [BC].
On en déduit que (AM), parallèle à (OA’), est perpendiculaire à (BC) ; c'est la hauteur (Ah_A) du triangle.
On montre, de même, que (BM) est aussi la deuxième hauteur (Bh_B) et on conclut que le point M, intersection de deux hauteurs, est l'orthocentre H du triangle ABC.

En remplaçant M par H on obtient la relation vectorielle = 2
et la relation d'Euler = + + .

Quel est le nom de la droite qui joint le centre du cercle circonscrit, le centre de gravité et l'orthocentre d'un triangle ?

La définition vectorielle du centre de gravité permet d'écrire
3 = + + donc = 3 .

Les points O, G et H sont alignés sur une droite dite droite d'Euler (1707-1783)
et GH = 2 GO (relation d'Euler : G est au tiers de [OH]).

Figure interactive dans GeoGebraTube : caractérisation de l'orthocentre

Voir : quatre relations d'Euler

1.c. Symétriques de l'orthocentre

Nous venons de démontrer que = 2 .
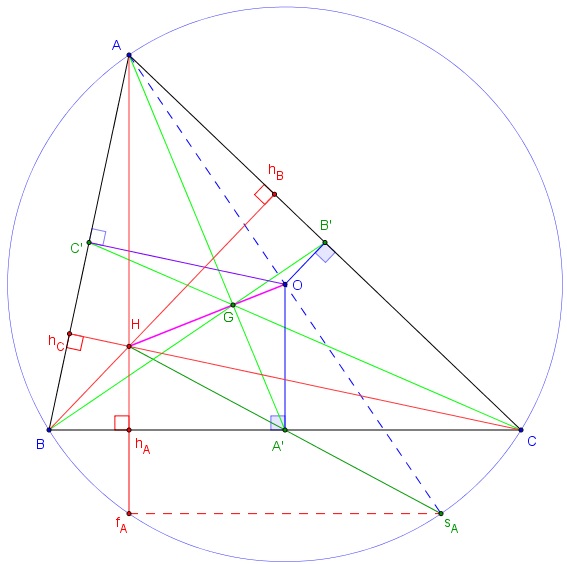
Soit s_A le symétrique de A par rapport à O
Dans le triangle AHs_A. la droite (OA’), passant par le milieu O du diamètre [As_A] et parallèle au côté (AH), est une droite des milieux de ce triangle.
A’ est le milieu de [Hs_A] et s_A est le symétrique de H par rapport à A’.

Les symétriques de l'orthocentre par rapport aux milieux des côtés du triangle sont situés sur le cercle circonscrit au triangle.

[As_A] est un diamètre. Le triangle Af_As_A, inscrit dans un demi-cercle, est rectangle. La droite (BC), perpendiculaire à (Af_A) est parallèle à (f_As_A) et passe par le milieu A’ de [Hs_A].
Dans le triangle Hf_As_A, (h_AA’) est la droite des milieux, h_A est milieu de [Hf_A].
(Hf_A) étant perpendiculaire à (BC), f_A est le symétrique de H par rapport à (BC).

Les symétriques de l'orthocentre par rapport aux côtés du triangle sont situés sur le cercle circonscrit au triangle.

Figure interactive dans GeoGebraTube : symétriques de l'orthocentre

Retrouver ces résultats avec l'homothétie entre le cercle circonscrit et le cercle d'Euler.

1.d. Droite d'Euler et triangle médian

geometrie du triangle - droite d'euler et triangle median - copyright Patrice Debart 2002

Autre démonstration en géométrie synthétique avec l'homothétie et les configurations fondamentales, sans utiliser les vecteurs.

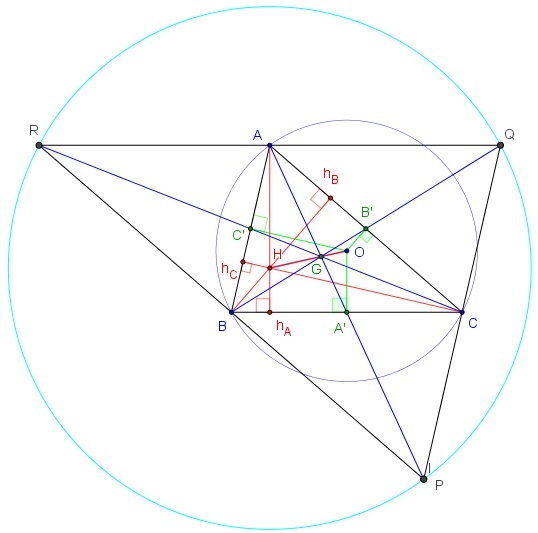
Soit PQR le triangle ayant ABC comme triangle médian.
P, Q et R sont les points d'intersection des parallèles aux côtés du triangle ABC passant par les sommets A, B et C.

La hauteur (Ah_A), perpendiculaire à (BC), est perpendiculaire à la parallèle (QR), en A milieu de [QR]. La hauteur issue de A est donc la médiatrice de [QR].

Les hauteurs du triangle ABC sont donc les médiatrices de PQR.
L'orthocentre H de ABC est le centre du cercle circonscrit à PQR.

(PA) médiane de PQR est une diagonale du parallélogramme ABPC. A’ milieu de [BC] est donc aussi le milieu de [PA] : les médianes (AA’) et (PA) sont confondues.
Les médianes de ABC et de PQR sont confondues.
G est le centre de gravité des triangles ABC et PQR.

L'homothétie H(G, –2) transforme le triangle ABC en PQR.
Dans cette homothétie, les images des médiatrices de ABC sont les médiatrices de PQR, hauteurs de ABC.
Le point O, centre du cercle circonscrit à ABC, a pour image le H, point d'intersection des médiatrices de PQR, orthocentre de ABC.
Les points O, G et H sont alignés, sur la droite d'Euler, et GH = 2 GO (relation d'Euler).

Figure interactive dans GeoGebraTube : droite d'Euler et triangle médian

Glossaire Publimath

WikiPédia : Triangle - Relation d'Euler

2. Cercle des neuf points d'Euler

de : Feuerbachkreis

geometrie du triangle - cercle des neuf points d'euler - copyright Patrice Debart 2019

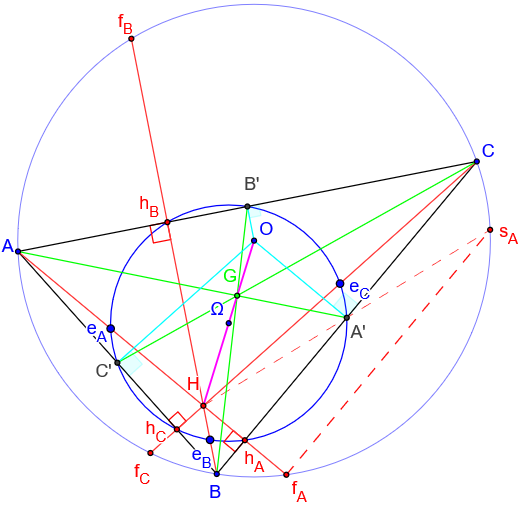
Le cercle d'Euler (1707-1783) passe par les neuf points suivants :
– les trois milieux des côtés du triangle A’ : B’ et C’ ;
– les trois pieds des hauteurs h_A; h_B et h_C ;
– les trois points d’Euler e_A; e_B et e_C ; milieux des segments [AH], [BH] et [CH] où H est l'orthocentre du triangle ABC.

Comme son nom ne le l'indique pas, le cercle d'Euler a été découvert en 1808 par Serge Brianchon (Paris, 1783-1864). On dit aussi cercle de Feuerbach ou cercle de Terquem.

(OH) est la droite d'Euler. Le centre de gravité G est au tiers de [OH] à partir du point O, centre du cercle circonscrit .
Le centre Ω du cercle d'Euler est le milieu de [OH].
Ω est le point X(5) dans ETC.

Le cercle des neuf points d'Euler est l'homothétique du cercle circonscrit au triangle dans les homothéties de centre G et de rapport – et de centre H et de rapport .

L'homothétie de centre G permet de mettre en place la droite et le cercle d'Euler.

L'homothétie de centre H permet de trouver les neuf points du cercle d'Euler comme points correspondants du cercle circonscrit.

Figure interactive dans GeoGebraTube : cercle d'Euler

Figure exportée dans WikiPédia, avec d'autres notations : cercle d'Euler

La droite d'Euler est la droite de Pascal de l'hexagramme A’h_BC’h_AB’h_C inscrit dans le cercle d'Euler du triangle ABC.

Indications

Nous avons vu au paragraphe précédent que l'homothétie de centre G et de rapport – transforme A en A’, B en B’ et C en C’.

Appelons cercle d'Euler le cercle circonscrit au triangle A’B’C’, homothétique du cercle circonscrit au triangle dans cette homothétie.

Reprenons les démonstrations sur les symétriques de l'orthocentre, étudiées ci-dessus :

A’ est l'image A par l'homothétie de centre G et de rapport – , nous avons donc = − .
Si s_A est le symétrique de A par rapport à O, dans le triangle AHs_A, (OA’) passant par le milieu O du diamètre [As_A] et parallèle au côté (AH) est une droite des milieux du triangle.
A’ est le milieu de [Hs_A] : s_A est le symétrique de H par rapport à A’.

2.b Symétriques de l'orthocentre et homothétie

Ici on utilise l'homothétie entre le cercle circonscrit et le cercle d'Euler pour retrouver les résultats du premier paragraphe : Symétriques de l'orthocentre

Les symétriques de l'orthocentre par rapport aux milieux des côtés du triangle sont situés sur le cercle circonscrit au triangle.

L'homothétie de centre H et de rapport , transforme s_A en A’, de même B’ et C’ sont les images des symétriques de l'orthocentre par rapport à ces milieux.
Le cercle d'Euler circonscrit au triangle A’B’C’ est l'image du cercle circonscrit à ABC, par l'homothétie.

On note f_A , le deuxième point d'intersection de la hauteur (Ah_A) avec le cercle circonscrit.
[As_A] en étant un diamètre, le triangle Af_As_A est inscrit dans un demi-cercle de centre O ; il est rectangle.

Les droites (BC) et (f_As_A), perpendiculaires à la Hauteur (Ah_A) sont parallèles.

Comme (s_AH) passe par le milieu A’ de [Hs_A], c'est une droite des milieux du triangle Hf_As_A, donc, h_A est milieu de [Hf_A].
(Hf_A) étant perpendiculaire à (BC), f_A est le symétrique de H par rapport à (BC).

Les symétriques de l'orthocentre par rapport aux côtés du triangle sont situés sur le cercle circonscrit au triangle.

h_A est le milieu de [Hf_A], c'est donc l'image de f_A par l'homothétie de centre H rapport .
Comme f_A e st situé sur le cercle circonscrit, h_A est sur le cercle d'Euler. Les pieds des hauteurs sont situés sur le cercle d'Euler.

L'homothétie de centre H transforme les sommets du triangle en les milieux des segments [AH], [BH] et [CH] qui sont trois derniers points situés sur le cercle d'Euler.

2.c. Le cercle d'Euler est le cercle circonscrit au triangle médian

geometrie du triangle - Les mediatrice du triangle median passe par le centre du cercle des 9 points - copyright Patrice Debart 2016

Le cercle circonscrit au triangle médian A’B’C’ est le cercle d'Euler du triangle ABC.

Les médiatrices du triangle médian sont concourantes au centre Ω du cercle des neuf points.

Figure interactive dans GeoGebraTube : cercle d'Euler circonscrit au triangle orthique

Glossaire Publimath

voir aussi : ellipse d'Euler – axe orthique

3. Centre d'Euler d'un quadrilatère

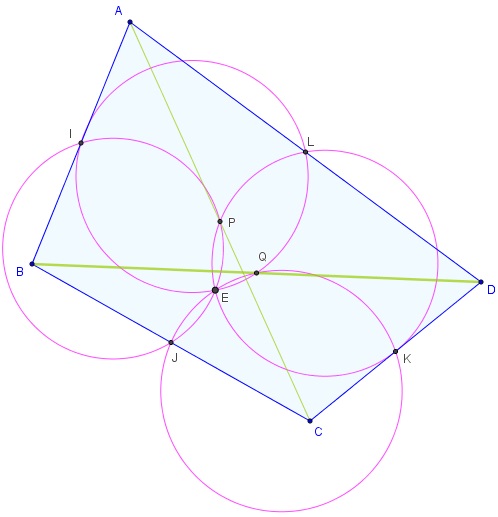
Dans un quadrilatère ABCD, soit I, J, K, L les milieux de ses côtés, et P, Q les milieux des diagonales [AC], [BD].

Les cercles d'Euler des quatre triangles ABC, BCD, CDA, DAB sont concourants en un point E appelé centre d'Euler du quadrilatère ABCD.

centre d'euler d'un quadrilatere - figure geogebra - copyright Patrice Debart 2018

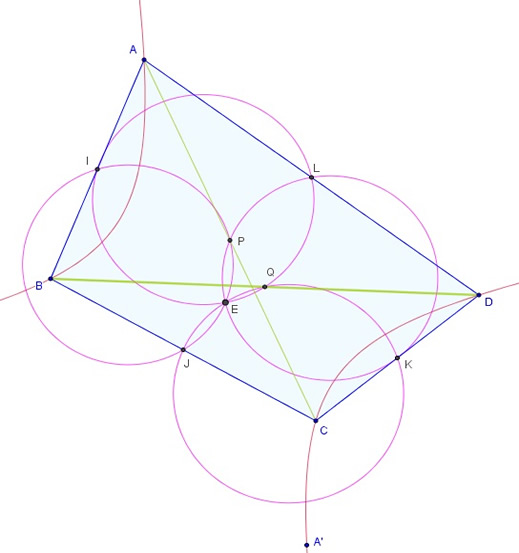
Hyperbole équilatère

hyperbole equilatere de centre le centre d'euler d'un quadrilatere - figure geogebra - copyright Patrice Debart 2018

Le centre d'Euler d'un quadrilatère ABCD est le centre de l'hyperbole équilatère - en général unique - passant par les 4 sommets A, B, C et D.

Pour tracer une conique, il faut cinq points. Avec GeoGebra tracer A' symétrique de A par rapport à E : instruction A’=Symétrie(A, E)

Puis l'hyperbole avec Conique(A, B, C, D, A’)

Figure interactive dans GeoGebraTube : centre d'Euler d'un quadrilatère

Centre d'Euler d'un quadrilatère inscriptible

centre d'euler d'un quadrilatere inscrit - figure geogebra - copyright Patrice Debart 2018

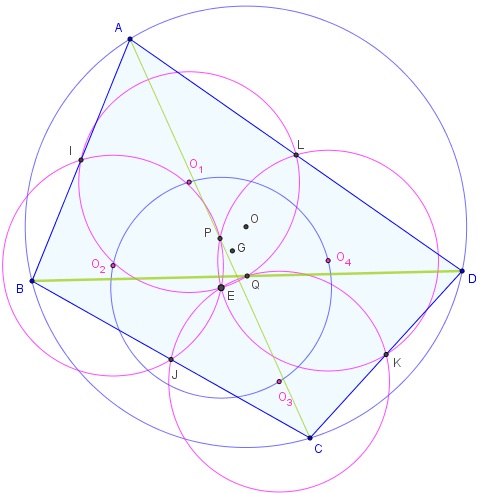
Si le quadrilatère ABCD est inscrit dans un cercle de centre O, alors les centres O₁, O₂, O₃ et O₄ des cercles d'Euler des triangles ABC, BCD, CDA, DAB sont cocycliques,
sur un cercle centré sur le centre d'Euler E du quadrilatère.

De plus, les centres E et O sont symétriques par rapport-au centre de gravité G du quadrilatère.

Figure interactive dans GeoGebraTube : centre d'Euler d'un quadrilatère inscrit