Descartes et les Mathématiques

Configurations fondamentales – Triangles

Exercices de maths en seconde sur le triangle. Problèmes de concours.

Sommaire

1. Droites perpendiculaires dans un triangle isocèle

2. Thalès et médiane

3. Problème de concours

4. Multiplication de l'aire d'un triangle

5. Partage d'un triangle en quatre

6. Ménélaüs

7. Médianes perpendiculaires dans un triangle

8. Construction de-ci, de-là

9. Triangles inscrits dans un triangle

Exemples d'exercices pouvant être résolus, en classe de seconde, avec les configurations fondamentales

Pour les triangles, il s'agit de savoir mettre en œuvre :
  – les propriétés des droites remarquables,

  – la droite des milieux et le théorème de Thalès,

  – les propriétés des angles et des aires des triangles,

  – les propriétés des triangles isocèles et équilatéraux,

  – les propriétés des triangles rectangles et l'inscription dans un demi-cercle.

En seconde la difficulté des raisonnements vient souvent de l'enchaînement de deux propriétés remarquables.

1. Droites perpendiculaires dans un triangle isocèle

Trois méthodes pour résoudre un exercice :
    – ici l'utilisation du parallélisme de la droite des milieux, ainsi que les propriétés de l'orthocentre et des hauteurs d'un triangle.
    – voir l'utilisation d'une similitude transformant deux triangles semblables
    – voir aussi en 1^ère S, une démonstration par le calcul d'un produit scalaire nul

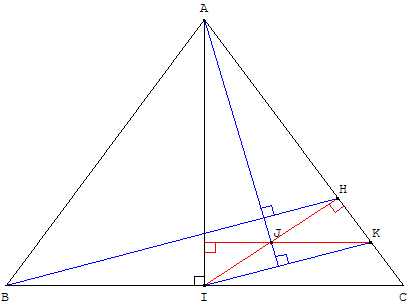
Exercice

Soit ABC un triangle isocèle en A, I le milieu de [BC], H le projeté orthogonal de I sur (AC), J le milieu de [IH].
Montrer que les droites (AJ) et (BH) sont perpendiculaires.

Faire intervenir (ce n'est pas évident) le milieu K de [HC].

Indications

Dans le triangle HIC la droite des milieux (KJ) est parallèle à (IC) donc orthogonale à (AI).
Dans le triangle AIK, les hauteurs (IH) et (KJ) se coupent en J qui est l'orthocentre du triangle.
(AJ) est alors la troisième hauteur, et est perpendiculaire à (IK).

Dans le triangle HCB, la droite des milieux (IK) est parallèle à (BH).
On a bien (AJ) perpendiculaire à (IK), donc perpendiculaire à la parallèle (BH).

Télécharger la figure GéoPlan confond1.g2w

2. Thalès et médiane

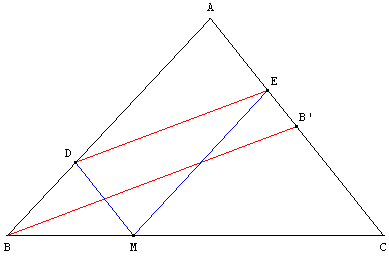
ABC est un triangle, [BB’] est une médiane.

M est le point du segment [BC] tel que BM = BC.
Les parallèles menées par M à (AC) et à (AB) coupent respectivement (AB) et (AC) en D et en E.

Calculer AD/AB et AE/AC.
Montrer que les droites (DE) et (BB’) sont parallèles.

Télécharger la figure GéoPlan triang_3.g2w

3. Problème de concours

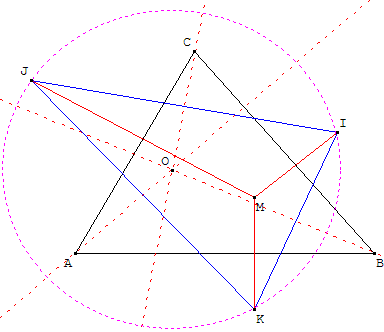
Soit ABC un triangle et M un point du plan.
I, J et K sont les symétriques du point M par rapport aux côtés du triangle ABC.

Soit (d₁) la perpendiculaire à (KJ) passant par A,
(d₂) la perpendiculaire à (IK) passant par B,
(d₃) la perpendiculaire à (IJ) passant par C.

Montrer que ces droites sont concourantes en O.
Ce sont les médiatrices du triangle IJK.

Télécharger la figure GéoPlan tria_sym.g2w

4. Multiplication par 7 de l'aire d'un triangle

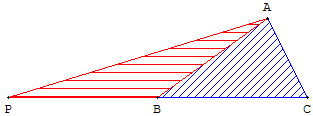
Deux triangles de même aire

ABC est un triangle d'aire a.

Sur la demi-droite [CB) on place le point P tel que BP = CB.

Le triangle PAB a pour aire a.

En effet les triangles ABC et PAB ont des bases de même longueur et une hauteur commune.

Triangle d'aire double

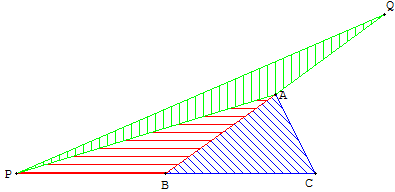
De même, sur la demi-droite [BA) on place le point Q tel que AQ = BA.
(PA) est une médiane du triangle PBQ.

Les triangles PAB et PAQ ont même aire a.
Le triangle PBQ a pour aire 2a.

Triangle d'aire sept fois plus grande

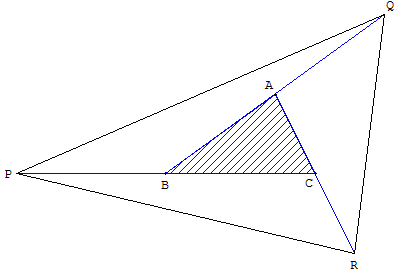
P est le symétrique de C par rapport à B, Q le symétrique de B par rapport à A
et R le symétrique de A par rapport à C.

On obtient un triangle PQR d'aire 7 fois celle du triangle ABC.

La démonstration se fait facilement en montrant que les aires des triangles PBQ, QAR et RCP sont égales à 2a.

Télécharger la figure GéoPlan mul_tria.g2w

Itération : Il est possible de répéter cette construction avec le triangle PQR, en traçant les symétriques des sommets, respectivement par rapport aux sommets consécutifs.
On obtient alors un nouveau triangle, 7 fois plus grand que PQR, d'aire 49 a.

Problème général : théorème de Routh

Sur la demi-droite [CB) on place le point P tel que BP = p CB,
sur la demi-droite [BA) on place le point Q tel que AQ = q BA
et sur la demi-droite [AC) on place le point R tel que CR = r AC.

GéoPlan calcule le rapport k = Aire(PQR)/Aire(ABC).

Pour p = q = r = 1, P est le symétrique de C par rapport à B, Q le symétrique de B par rapport à A et R le symétrique de A par rapport à C.
On retrouve alors le problème ci-dessus.

Si I, J et K sont les points d'intersection des droites (QB), (PC) et (RA) avec les côtés du triangle PQR (voir figure ci-dessous), on montrera, en première S avec des barycentres, que dans ce cas les points I, J et K sont situés au tiers des côtés de ce triangle.

4.b. Problème réciproque

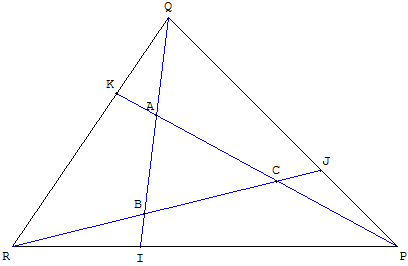
Retrouver le triangle ABC à partir du triangle PQR.

Sur les côtés du triangle PQR, placer les points I, J, K tels que :
RI = k RP,
PJ = k PQ,
QK = k QR.

A, B et C sont les points d'intersection des droites (PK), (QI) et (RJ).

Figure pou k = 1/3.

Dans ce cas, si S = Aire(PQR), alors Aire(ABC) = S/7.

On le démontre avec les aires des triangles APQ, BRQ et CRP égales à 2S/7.
On peut remarquer que les aires des quadrilatères ABKR, ... sont égales à 5S/21
et que les aires des triangles AQK, BRI et CPI sont égales à S/21.

Télécharger la figure GeoGebra triangle 7 fois plus petit

Voir : Multiplication des parallélogrammes

Problèmes de partage

Jeu géométrique

Problème du triangle d'aire un septième de celle d'un triangle donné : applicton du théorème de Routh

Pour k = ou k = , on a l'exercice réciproque : étant donné un triangle PRQ, construire trois points A, B et C de telle sorte que B soit le milieu de [PC], C soit le milieu de [RA] et A soit le milieu de [QB].
Calculer l'aire de ABC.

Solution

Placer I, J et K comme dans la figure ci-contre, avec k = .

Avec la propriété des proportions : Aire(PQI) = Aire(PQR).
A est le barycentre de (P,1) ; (Q, 4) ; (R, 2) ;
B est le barycentre de (P,2) ; (Q, 1) ; (R, 4) ;
C est le barycentre de (P,4) ; (Q, 2) ; (R, 1).

D'où QB = 6/7 QI et Aire(PQB) = 6/7 Aire(PQI).
De plus QA = 3/7 QI = QB ; A est le milieu de [QB]
et Aire(PAB) = Aire(PQB).

De même PA = 6/7 PK et PC = 3/7 PK = PA.
C est le milieu de [PA] et Aire(CAB) = Aire(PAB).

Enfin RB = 3/7 RJ et B est le milieu de [PC].

En regroupant les égalités d'aires, on a :
Aire(CAB) = Aire(PAB) = 1/4 Aire(PQB) = 1/4 × 6/7 Aire(PQI) ;
Aire(CAB) = 3/14 × 2 /3 Aire(PQR) ;

Aire(ABC) = 1/7 Aire(PQR).
Le triangle ABC est bien 7 fois plus petit que le triangle PQR.

5. Partage d'un triangle en quatre

Partage non trivial d'un triangle ABC en quatre triangles d'aires égales, sans utiliser de milieux.

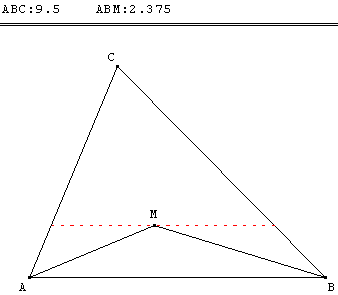
Grâce à une première recherche avec GéoPlan, on trouve qu'un triangle ABM a une aire égale au quart de celle du triangle ABC lorsque le point M est sur la parallèle à (AB) qui coupe le segment [AC] au quart à partir de A.
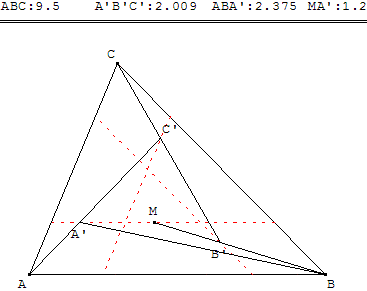
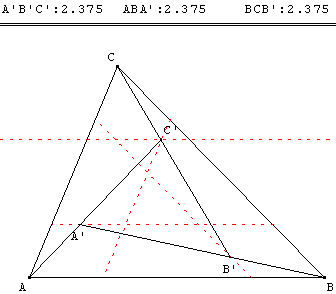
Un partage de ABC se fera donc en plaçant trois points A’, B’, C’ sur des parallèles aux côtés situées comme si dessous.

Une recherche avec GéoPlan consistera, à partir d'un point M variable sur le segment parallèle à (AB), à placer le point B’, intersection de (BM) et de la parallèle à (BC) ; C’ puis A’ aux intersections des parallèles avec (CB’) et (AC’).

Déplacer le point M pour le faire coïncider avec le point A’. Les points A, A’, C’ forment alors une section d'or, le rapport est égal au nombre d'or φ = .

On trouve donc la solution à partir du point C’ situé à l'intersection de la droite parallèle à (AC) et de la droite (d) image de la parallèle à (AB)
par l'homothétie de centre A et de rapport 1 + .

Télécharger la figure GéoPlan tri_4_partage.g2w,

    la figure GéoPlan tri_4_partage_2.g2w

Voir : partage en deux d'un triangle

partage en deux polygones d'un triangle.

6. Théorème de Ménélaüs

Ménélaüs d'Alexandrie : mathématicien grec de la fin du I^er siècle, auteur de trois livres, dont les sphériques consacré aux triangles sur une sphère.

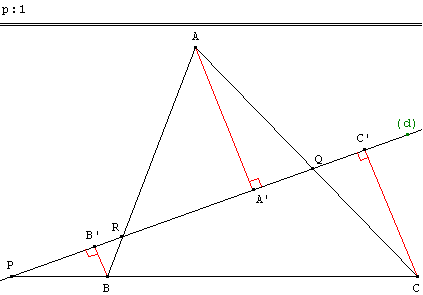
Soit ABC un triangle et (d) une droite ne contenant aucun des sommets.
La droite (d) rencontre (BC) en P, (CA) en Q et (AB) en R.

On a × × = 1.

Un curieux point de concours : voir produit scalaire

Méthode à mettre en œuvre

On appelle A’, B’ et C’ les projetés orthogonaux de A, B et C sur (d).

La propriété de Thalès dans les triangles semblables permet d'écrire :
(BB’)//(CC') ; PBB’ semblable à PCC’ : = ,
(CC’)//(AA’) ; QCC’ semblable à QAA’ : = ,
(AA’)//(BB’) ; RAA’ semblable à RBB’ : = .

D'où par multiplication × × = × × = 1.

Réciproque

Soit ABC un triangle, P un point de (BC), Q point de (CA) et R point de (AB) ; (P, Q et R distincts des sommets).

Il existe trois nombres a, b et c différents de 0 et 1
tel que = a , = b , = c .

Si abc = 1, les points P, Q et R sont alignés.
La droite (PQ) est alors appelée « ménélienne » du triangle ABC (transversale ne passant pas par un des sommets).

Télécharger la figure GéoPlan menelaus.g2w

7. Médianes perpendiculaires dans un triangle

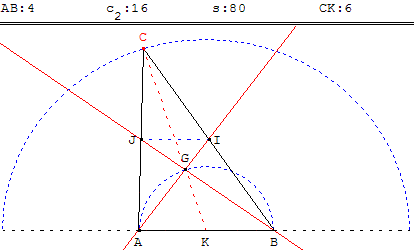
Dans la figure ci-contre, le triangle ABC est « orthomédian » en A et B :
les médianes issues de ces deux sommets sont perpendiculaires.

Construire ce triangle.

Calculer la somme CA² + CB² des carrés des deux côtés, en fonction du carré AB², du troisième ?

Solution

Si les médianes relatives à deux côtés d'un triangle sont perpendiculaires, la somme des carrés de ces côtés est égale à cinq fois le carré du troisième.

Preuve, classe de seconde

Une utilisation répétée de la propriété de Pythagore dans les quatre triangles rectangles en G permet d'écrire :
triangle AJG : CA² = 4 AJ² = 4 GA² + 4 GJ²,
triangle BIG : CB² = 4 BI² = 4 GB² + 4 GI².

En ajoutant membre à membre : CA² + CB² = 4 (GA² + GB²) + 4 (GI² + GJ²) = 4 AB² + 4 IJ²
Or d'après la propriété des milieux dans ABC : AB = 2 IJ, soit 4 IJ² = AB². D'où :

CA² + CB² = 5 AB².

Preuve, classe de première

Le triangle ABG, rectangle en G, est inscrit dans le cercle de diamètre [AB] de centre K. Le rayon GK est égal à la moitié du diamètre AB.
Le centre de gravité G est situé aux deux tiers de la médiane [CK], donc CK = 3 GK = AB.

D'après le théorème de la médiane, on a :
CA² + CB² = 2 CK² + = AB² + d'où CA² + CB² = 5 AB².

Télécharger la figure GéoPlan mon_379.g2w

Problèmes de construction : construire un triangle connaissant deux sommets et le centre de gravité

 Construire un triangle connaissant ses médianes

Barycentre

Symédianes et point de Lemoine : points caractéristiques du triangle

Produit scalaire

8. Construction de-ci, de-là

Existe-t-il un triangle ABC tel que la hauteur issue de A, la bissectrice de l'angle BÂC et la médiane relative au côté [BC] partagent l'angle BÂC en quatre angles de même mesure ?

Solution

ABC est un triangle rectangle en A, l'angle droit est partagé en quatre angles de 22,5°. Un angle aigu du triangle mesure 22,5° et si O est le milieu de [BC], la médiane (AO) fait un angle de 45° avec l'hypoténuse.

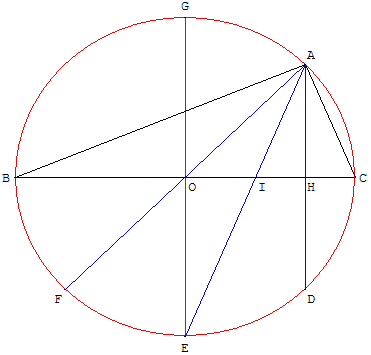
Indications

Soit le triangle ABC une solution, O le milieu de [BC] et (c) son cercle circonscrit.
La hauteur (AH) issue de A recoupe le cercle circonscrit (c) en D, la médiane (AO) en F et la bissectrice (AI) de l'angle BÂC en E.

Le point E, milieu de l'arc BC, est situé sur la médiatrice de [BC], la droite (OE). Les droites (OE) et (AD), perpendiculaires à (BC) sont parallèles ; elles forment avec la droite (AF) des angles FÔE et FÂD égaux. (AE) est la bissectrice de FÂD donc FÔE = 2 FÂE.

Le centre du cercle circonscrit est situé sur la médiatrice de [AB] ; le diamètre [EG] : FÔE est l'angle au centre de l'angle inscrit FÂE, le point O est alors le centre du cercle circonscrit.

Le triangle ABC est rectangle en A, les points D, E et F partagent le demi-cercle en quatre arcs égaux. Les points A et D sont symétriques par rapport à la droite (BC), A est le milieu de l'arc CG.

Programme de construction

Tracer un cercle (c) et deux diamètres [BC] et [EG] perpendiculaires. Tracer les deux bissectrices de ces diamètres qui coupent le cercle en A et F pour l'une, et en D pour l'autre ; les points A et D étant d'un même côté de la droite (EG). Le triangle rectangle ABC est une solution du problème et les trois droites remarquables (AD), (AE) et (AF) partagent l'angle BÂC en quatre angles de 22,5°.

Relations métriques

Soit r le rayon du cercle circonscrit. Dans le triangle rectangle isocèle AHB on a OH = AH = r.

BH = BO + OH = r + r = (2 + ) et HC = OC – OH = r – r = (2 – ).

Dans le triangle rectangle ABH la propriété de Pythagore permet d'écrire
AB² = AH² + BH² = + (2 + )² = [2 + (2 + )²] = [8 + 4] = r² (2 + ).

AB = r .

Un calcul analogue dans le triangle rectangle AHC donne
AC² = r² (2 – ) et AC = r .

On trouve les lignes trigonométriques cos 22,5° = et sin 22,5° = .

Généralisation : calcul des valeurs trigonométriques de l'angle moitié :

soit OAH un triangle rectangle en H, d'hypoténuse [OA] de longueur 1, dont on connaît cos Ô ou sin Ô.
En plaçant sur la droite (OA) les deux points B et C à une distance 1 de O, le point C sur la demi-droite [OH), on obtient un triangle ABC d'angle ABC = . Dans les triangles rectangles AHB et AHC, le calcul de AB et AC en fonction de OH = cos Ô et de AH = sin Ô,
permet d'en déduire cos() = AB et sin() = AC.

Olympiades 2008 - Montpellier

Réciproque : prouver qu'un rectangle ayant angle partagé en 4 angles de même mesure par la hauteur, la bissectrice et la médiane issues du sommet de cet angle, dans cet ordre, est obligatoirement rectangle.

Télécharger la figure GéoPlan trois_bissect.g2w

9. Triangles inscrits dans un triangle

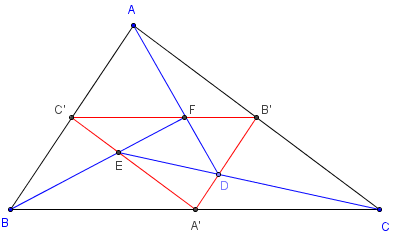
Figures de Morgane le Gall pour Le Monde Science & Techno : à qui appartient le savoir, 2 mars 2013.

Dans la figure ci-contre, commet construire les triangles DEF ?

Conjecture

Par Thalès on a l'égalité des rapports :
A’D/A’B’ = ED/EC ; B’F/B’C’ = DF/DA ; C’E/C’A’ = FE/FB.

Tous ces rapports semblent être égaux entre eux.
En plaçant D sur [A’B’] tel que A’D/A’B’ = 0,382, le point F, intersection de (BE) et [B’C’], apparaît être sur [AD].

Télécharger la figure GeoGebra triangle_inscrit.ggb

ABC triangle équilatéral

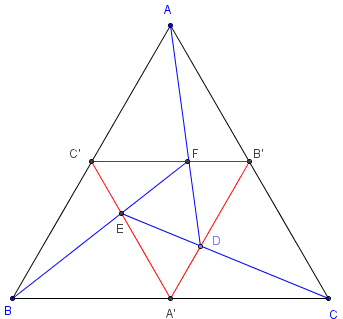
Télécharger la figure GeoGebra triangle_equi_inscrit.ggb

Ci-dessous, le point D est placé manuellement sur [AA’], en le déplaçant de telle façon que le point F, intersection de [A’E] et [CC’], semble être sur (B’D).

Peut-on trouver une construction à la règle et au compas ?

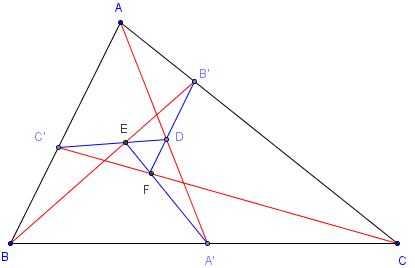
Conjecture

AD/AA’ = BE/BB’ = CF/CC’.

Télécharger la figure GeoGebra triangle_inscrit2.ggb