Descartes et les Mathématiques

Produit scalaire

Exercices de 1^ère S résolus par le calcul de produits scalaires : application à des triangles, des trapèzes ou des carrés…

Sommaire

Définitions

1. Hauteur et médiane d'un triangle rectangle

2. La médiane de l'un est la hauteur de l'autre

3. Dans la foulée : droites perpendiculaires

4. Triangle rectangle isocèle

5. Trapèze rectangle

6. Un curieux point de concours

7. Hauteur d'un triangle

8. Quadrilatère inscriptible orthodiagonal

II. Exercices

1. Droites perpendiculaires
2. Calculs d'angles
3. Triangulation
4. Équations de cercles en géométrie analytique
5. Lieux de points
6. Hauteur d'un triangle

7. Produit scalaire et théorème de la médiane

Définitions du produit scalaire

Dans un espace vectoriel réel, le produit scalaire est une opération algébrique, s'ajoutant aux lois s'appliquant aux vecteurs, qui. à deux vecteurs associe un nombre réel (scalaire).

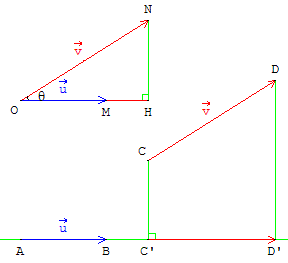
Définition 1 (projection orthogonale)

Le produit scalaire de deux vecteurs et colinéaires est égal à AB × CD s'ils sont de même sens, et à – AB × CD s'ils sont de sens contraires.
Pour calculer le produit scalaire . de deux vecteurs non colinéaires, on peut remplacer le vecteur par sa projection orthogonale sur le vecteur .

Sur la figure . = . = . = AB × C’D’ (car et sont de même sens).

Définition simple et intuitive issue de l'expérience physique du travail d'une force. Il faut démontrer, ou admettre, que le produit scalaire est indépendant du choix des bipoints représentant les vecteurs.

Télécharger la figure GéoPlan p_s_def.g2w

Définition 2 (expression analytique dans le plan)

Si dans un repère orthonormal (O, , ), et ont pour coordonnées respectives (x, y) et (x’, y’), alors . = xx’ + yy’.

Définition simple et calculs faciles. On retrouve xx’ + yy’ = 0 pour les vecteurs orthogonaux.
On retrouve aussi le calcul de distance de deux points : |||| = = AB, où x et y sont les coordonnées de .
Il faut admettre que le calcul du produit scalaire est indépendant du choix du repère.

Définition 3 (expression trigonométrique à l'aide des normes et d'un angle)

. = |||| × |||| × cos θ, où θ est l'angle (, ) formé par les directions des vecteurs.

Ci-déssus, sur la figure en haut à droite, en choisissant deux vecteurs de même origine O :
. = . = . = OM × ON × cos θ.

Si – < θ < , . = . = OM × OH,
si < |θ| < π, . = . = − OM × OH.

Définition 4 (carré des normes)

si = , |||| = |||| = AB.

On appelle produit scalaire de deux vecteurs le nombre : . = [ || + ||² – ||||² – ||||² ].

. se note ² = ||||² et si = , alors ² = ² = ||||² = AB².

Définition, un peu délicate, du produit scalaire comme forme bilinéaire symétrique définie positive.
Comme souvent avec les mathématiques modernes c'est simple, les calculs sont faciles, mais trop abstraits.

Application
Calculer une longueur avec le produit scalaire : si = , alors AB² = ² = ².

Remarque : il est intéressant de faire le lien entre ces quatre définitions

Règles de Calcul

Commutativité : . = ..

Les propriétés de bilinéarité suivantes sont valables :
distributivité : .( + ’) = . + .’; ( + ’). = . + ’.,
Multiplication par un réel : (k). = k (.) ; .(k) = k (.).

Orthogonalité

Si deux vecteurs sont perpendiculaires entre eux, le produit scalaire est nul.

1. Hauteur et médiane d'un triangle rectangle

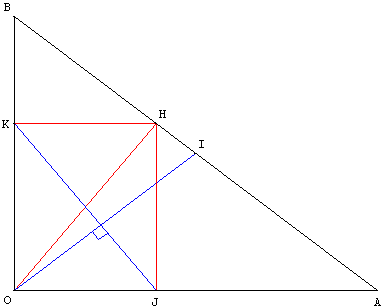
Le triangle OAB est rectangle en O.

(OI) est la médiane et (OH) la hauteur issues de O.

Le point H se projette orthogonalement en J et K sur les petits côtés du triangle.

Montrer que les droites (OI) et (JK) sont orthogonales.

Télécharger la figure GéoPlan p_s_tri.g2w

Voir une recherche et deux démonstrations avec les angles et aussi par des relations de parallélisme et d'orthogonalité dans : orthogonalité dans un triangle rectangle.

2. La médiane de l'un est la hauteur de l'autre

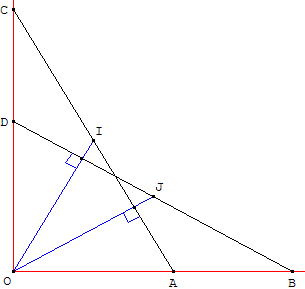
Soit A et B deux points sur la demi-droite (Ox).

Sur la demi-droite (Oy) on place les points C et D tel que OC = OB et OD = OA.

I est le milieu de [AC].

Montrer que la médiane (OI) du triangle OAC est la hauteur du triangle OBD.

De même, la médiane (OJ) du triangle OBD est la hauteur du triangle OAC.

Télécharger la figure GéoPlan med_haut.g2w

Voir : les problèmes du BOA

Similitudes au bac

3. Dans la foulée : droites perpendiculaires

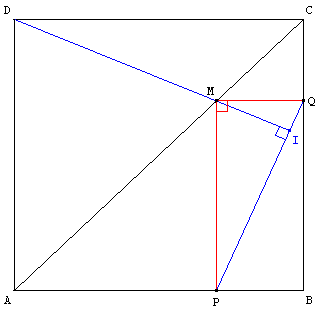
M est un point variable de la diagonale [AC] d'un carré ABCD, distinct de A et C.

Il se projette en P et Q sur les étés [AB] et [BC] du carré.

Montrer que la droite (DM) est perpendiculaire à (PQ).

Télécharger la figure GéoPlan p_s_ca2.g2w

4. Triangle rectangle isocèle variable

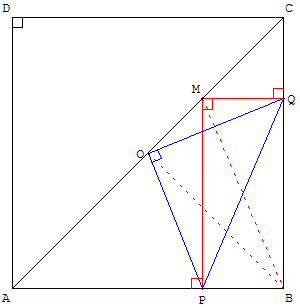
M est un point variable de la diagonale [AC] d'un carré ABCD, distinct de A et C.
Il se projette en P et Q sur les étés [AB] et [BC] du carré.

Si O est le milieu du carré, montrer que OPQ est un triangle rectangle isocèle.

Indications

Calculer le produit scalaire . :

. = ( + ).( + ) = ² + .( + ) + . = ² + .() + 0.
Or le produit scalaire . est égal au produit de par la projection de sur (OM)
soit . = − ².
. = ² − ² = 0, l'angle PÔQ est droit.

La rotation de centre O et d'angle , transforme les droites (AB) en (BC), (OP) en (OQ) ; leurs points d'intersection P en Q.
Donc, OP = OQ et le triangle OPQ est rectangle isocèle en O.

 Bibliographie : angles et rotations – brochure IREM – Bordeaux 1996

Télécharger la figure GéoPlan p_s_ca3.g2w

5. Diagonales orthogonales d'un trapèze rectangle

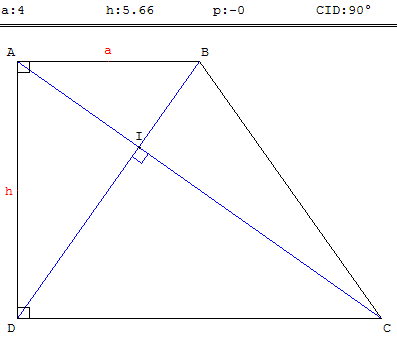
Rappel : Un trapèze rectangle est un trapèze qui possède un angle droit.
Si ce n'est pas un carré, le trapèze rectangle a deux angles droits.

Énoncé

ABCD est un trapèze rectangle en A et D tel que la petite base AB = a, la grande base DC = 2a
et la hauteur AD = h.

Sachant que = + , calculer le produit scalaire . en fonction de a et de h.

Trouver la valeur h pour laquelle les diagonales [AC] et [BD] sont orthogonales.

Recherche avec GéoPlan

Modifier h avec les flèches du clavier.

Indication

La solution correspond à la valeur : h = a . Avec GéoPlan, taper S pour obtenir la figure correspondant à cette Solution.

Télécharger la figure GéoPlan trap_rec.g2w

6. Un curieux point de concours

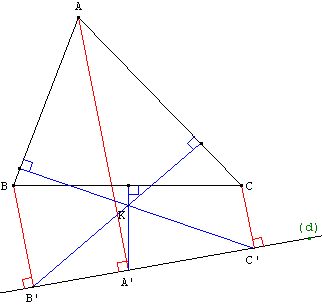
On projette orthogonalement les sommets d'un triangle ABC sur une droite d en A’, B’ et C’.

Soit d₁ la droite passant par A’ perpendiculaire à (BC),
d₂ la droite passant par B’ perpendiculaire à (AC),
d₃ la droite passant par C’ perpendiculaire à (AB).

Montrer que les droites d₁, d₂ et d₃ sont concourantes.

Méthode à mettre en œuvre

Les droites d₂ et d₃ sont concourantes en K.

Montrer que le produit scalaire des vecteurs . est nul en décomposant :
 =  + et = + .
La droite (KA’) est orthogonale à (BC), c'est la droite d₁ qui passe par K.

Télécharger la figure GéoPlan pt_conco.g2w

Théorème de Ménélaüs : configurations fondamentales

Démonstration comme point de concours de trois axes radicaux : géométrie du cercle

7. Hauteur d'un triangle

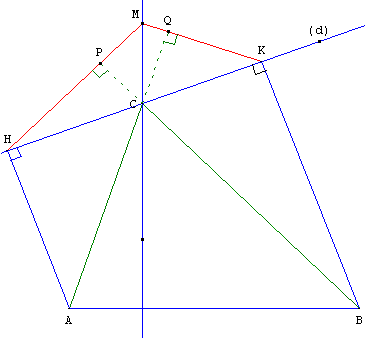
Cas particulier de l'exercice précédent lorsque la droite (d) passe par un sommet du triangle.

On considère un triangle ABC et une droite (d) passant par C.
On désigne par H et K les projetés orthogonaux de A et B sur (d) et, par M le point d'intersection de la perpendiculaire menée de H à (BC) et de la perpendiculaire menée de K à (AC).

Démontrer avec un calcul de produit scalaire que les droites (CM) et (AB) sont orthogonales :

Par projection sur la droite (AC) :

. = . et . = . d'où . = .

Par projection sur la droite (d) : . = . donc . = .

Par projection sur la droite (BC) :. = . et . = . d'où . = .

Par projection sur la droite (d) : . = . donc . = .

Soit . = . = . d'où . – . = 0 et ( – ). = ( + ). = . = 0.

Le produit scalaire est nul, et les droites sont bien perpendiculaires.

Lorsque la droite (d) tourne autour du point C, le point M décrit la hauteur issue du C sur (AB) du triangle ABC.
Si la droite (d) est confondue avec un des côtés (AC) ou (BC) du triangle, le point M est l'orthocentre du triangle.

Télécharger la figure GéoPlan ps_hauteur.g2w

Famille de cercle : épreuve pratique en terminale S

8. Quadrilatère inscriptible orthodiagonal

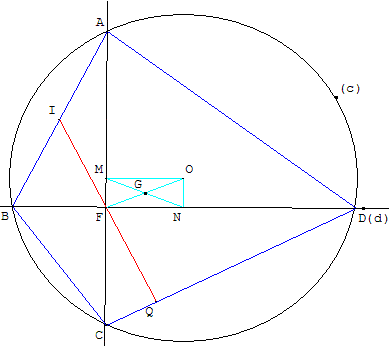
Soit (c) un cercle de centre O, de rayon r.
F un point à l'intérieur du cercle, distinct de O.

Deux droites (d) et (d₂) orthogonales pivotent autour du point F.
La droite (d) coupe le cercle (c) en A et C, (d₂) coupe (c) en B et D.

Les points cocycliques A, B, C et D forment le quadrilatère orthodiagonal ABCD.

Soit I, J, K, L les milieux des cordes [AB], [BC], [CD], [DA].

Le point G, centre de gravité de ABCD, est un point fixe :
soit M le milieu de [AC], N milieu de [BD]. G est le centre du rectangle OMFN. C'est donc le milieu de [OF].

La somme FA² + FB² + FC² + FD² = 4r² est indépendante de F.
On a aussi : AB² + CD² = AD² + CB² = 4r².

Soit Q le projeté orthogonal de F sur [CD].

La médiane (FI) du triangle AFB est la hauteur (FQ) du triangle CFD.

Télécharger la figure GéoPlan qua_insc.g2w

Voir : théorème de Brahmagupta : le cercle en seconde

quadrilatère orthodiagonal (et son aire)

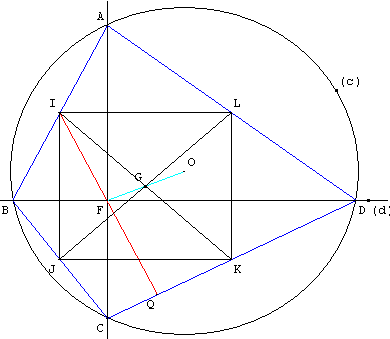
Le quadrilatère de Varignon IJKL est un rectangle de centre G.

Télécharger la figure GéoPlan qua_ins2.g2w

Cercle des huit points d'un quadrilatère inscriptible orthodiagonal

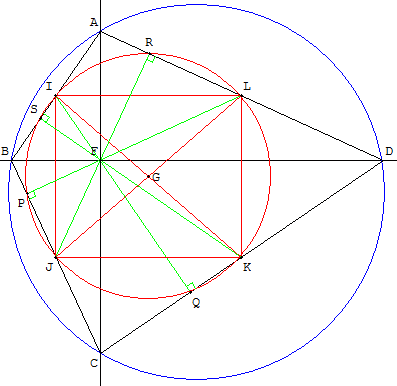
Soit I, J, K, L les milieux des cordes [AB], [BC], [CD], [DA] et S, P, Q, R les projetés orthogonaux de F sur ces cordes.

Les huit points I, J, K, L, P, Q, R, S appartiennent à un même cercle (cercle fixe de centre G).

Télécharger la figure GéoPlan qua_insc_cercle8p.g2w

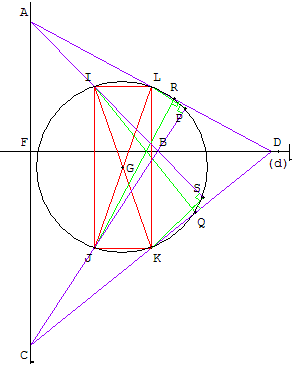
Cercle des huit points d'un quadrilatère dont les diagonales sont perpendiculaires.

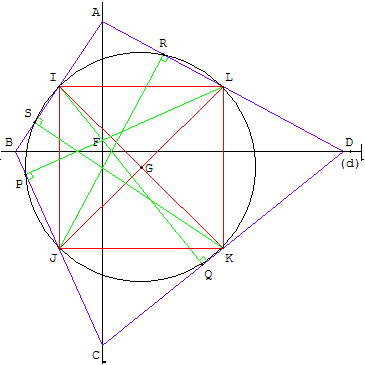
Soit I, J, K, L les milieux des cordes [AB], [BC], [CD], [DA] et R, S, P, Q les projetés orthogonaux de ces quatre milieux sur les cordes opposées.

Les huit points I, J, K, L, P, Q, R, S appartiennent toujours à un même cercle.

Vérifier que ce résultat est encore vrai pour un quadrilatère non convexe dont les diagonales sont perpendiculaires.

Télécharger la figure GéoPlan cercle8p.g2w

Bibliographie : Sortais Yvonne et René – Géométrie – Hermann 1988
Imagiciels orthocor – Géométrie plane – MEN 1992

II. Exercices

II.1. Droites perpendiculaires

1.a. Droites perpendiculaires dans un rectangle

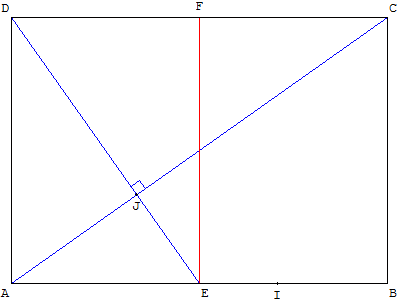
Rectangle ayant le format du papier A4

ABCD est un rectangle de largeur AD = a et de longueur AB = a.
E est le milieu de [AB].
Que peut-on dire des droites (AC) et (DE) ?

Télécharger la figure GéoPlan rectangle.g2w

Indication

Calculer le produit scalaire . dans le repère orthonormé (A, , ) où I est le point de [AB] tel que AI = a.

Remarque : Soit J le point d'intersection des droites (AC) et (DE).
La similitude de centre J, d'angle , et de rapport transforme le rectangle ABCD en EFDA. la diagonale [AC] est transformée en [DE]. l'angle de ces deux droites est égal à l'angle de la similitude. Elles sont bien perpendiculaires.

1.b. Droites perpendiculaires

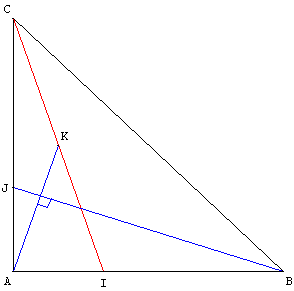
Droites perpendiculaires dans un triangle rectangle isocèle

Soit ABC un triangle rectangle isocèle en A.
Soit I le point de [AB] tel que AI = ;
J le point de [AC] tel que AJ = ; et K le milieu de [IC].

Démontrer que les droites (AK) et (JB) sont perpendiculaires.

Télécharger la figure GéoPlan tr_rec_iso.g2w

1.c. Droites perpendiculaires dans un triangle isocèle

Trois méthodes pour résoudre un exercice :
    – ici démonstration par le calcul d'un produit scalaire nul
    – voir l'utilisation d'une similitude transformant deux triangles

    – voir aussi les configurations fondamentales, dans triangle en seconde

Exercice

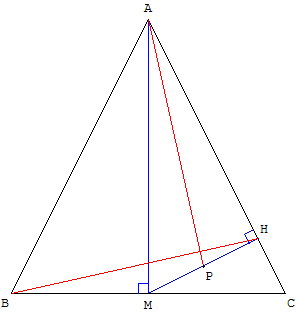
ABC est un triangle isocèle en A.
Le milieu M de [BC] se projette orthogonalement en H sur (AC).
P est le milieu de [MH].

Pourquoi les droites (BH) et (AP) sont-elles perpendiculaires ?

Indication

Calculer le produit scalaire
. = ( + ) . ( + )

D'où
. = ( + /2) . ( + ).

Développer 2 . , et en factorisant , montrer que le produit scalaire est nul.

Télécharger la figure GéoPlan tr_iso.g2w

II.2. Calculs d'angles

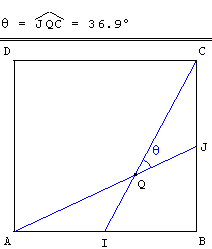
Droites joignant des sommets d'un carré aux milieux des côtés

Les points I et J sont les milieux des côtés [AB] et [BC] d'un carré ABCD (où AB = a, a > 0).
On note θ l'angle (, ). Donner une valeur exacte de cos θ, puis une valeur approchée de θ en degré à 0,1° près.

Indication

Utiliser l'expression trigonométrique du produit scalaire :

, = AJ × IC × cos θ.

Télécharger la figure GéoPlan carré_1.g2w

Mesure d'un angle du cerf-volant AICJ

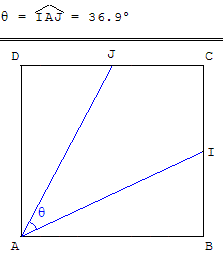
Les points I et J sont les milieux des côtés [BC] et [CD] d'un carré ABCD (où AB = a, a > 0).
On note θ l'angle (, ).

Avec l'expression trigonométrique du produit scalaire, donner une valeur exacte de cos θ, puis une valeur approchée de θ en degré à 0,1° près.

Télécharger la figure GéoPlan carre_2.g2w

Variante : calculer l'angle (, ).

Autres carrés, voir la page : rotation

II.3. Triangulation

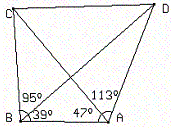
À partir de deux points, sur la côté AB, on vise deux îlots C et D dont on veut calculer la distance.

Les angles suivants ont été mesurés à partir de deux points A et B distants d'un kilomètre :
BÂC = 47°; DÂB = 113°; ABD = 39° et ABC = 95°.

Calculer les distances AC, AD et CD.

II.4. Équations de droites et cercles

Rappels du cours de géométrie analytique

« Si (a, b) est un vecteur normal d'une droite (d) passant par un point A, alors (d) est le lieu des points M(x, y) tel que . = 0 ;
une équation de (d) s'écrit sous la forme ax + by + c = 0 ».
Réciproquement, si a et b sont deux réels non nuls, l'équation ax + by + c = 0 est l'équation d'une droite dont le vecteur de coordonnées (a, b) est un vecteur normal.

Application : équation de la médiatrice d'un segment [AB] ; droite passant par le milieu I de [AB], orthogonale au vecteur .

« Le cercle de centre I(a, b) et de rayon r est l'ensemble des points M(x, y) tel que IM² = r² ».
Une équation de ce cercle est : (x – a)² + (y – b)² = r² ; soit x² + y² – 2ax – 2by + c = 0.
Le cercle de diamètre [AB] est l'ensemble des points M du plan tel que : . = 0 soit (x – x_A) (x – x_B) + (y – y_A) (y – y_B) = 0.

Application : soit (c) un cercle de centre I et A un point de (c). Pour la tangente en A au cercle (c), écrire l'équation de la droite passant par A, orthogonale au vecteur .

Triangle

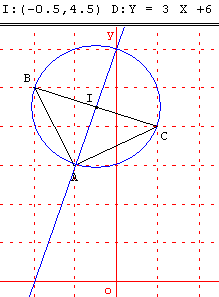
Dans un repère orthonormé, on donne les points : A(–1, 3) ; B(–2, 5) et C(1, 4).

5.a. Démontrer que le triangle ABC est rectangle et isocèle en A.

5.b. Déterminer une équation du cercle circonscrit au triangle ABC.

5.c. Déterminer une équation de la médiatrice de [BC].

Télécharger la figure GéoPlan tr_cer_cir.g2w

Deux cercles

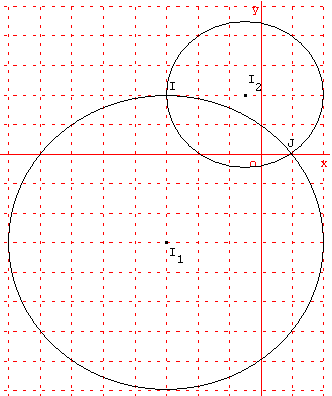
On définit les cercles (c₁) et (c₂) par les équations suivantes :
(c₁) : x² + y² + 6x + 6y – 7 = 0,
(c₂) : x² + y² + x – 4y – 2 = 0.

a. Déterminer les coordonnées des centres I₁ et I₂, les rayons r₁ et r₂ de ces deux cercles et les tracer.
b. Quelles sont les coordonnées des points d'intersection I et J de ces deux cercles.

Télécharger la figure GéoPlan deux_cercles.g2w

II.5. Lieux de points

Soit A et B deux points du plan tel que AB = 5 (l'unité est égale à 1 cm) et I est le milieu de [AB].
6.a. Dire quel est l'ensemble (c₁) des points M tel que . = 0.
Construire (c₁).
6.b. Dire quel est l'ensemble (d₁) des points M tel que . = −10.
Construire (d₁).
6.c. Dire quel est l'ensemble (d₂) des points M tel que MA² – MB² = 10.
Construire (d₂).
6.d. Dire quel est l'ensemble (d₃) des points M tel que ( + ). = 0.
Construire (d₃).
6.e. Dire quel est l'ensemble (c₂) des points M tel que . = −4.
Construire (c₂).

II.6. Hauteur d'un triangle

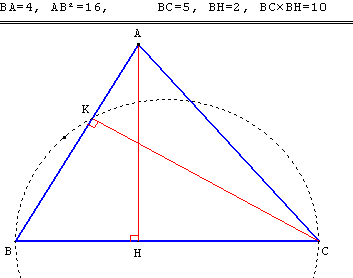
Dans un triangle ABC, on nomme H le pied de la hauteur issue de A et K le pied de la hauteur issue de C.

7.a. Prouver que . = .

7.b. En déduire que le triangle ABC est rectangle en A,
si et seulement si BA² = .

7.c. La relation BA² = BH × BC implique-t-elle que le triangle ABC soit rectangle en A ?
Construire un contre-exemple.

Télécharger la figure GéoPlan tr_hautr.g2w

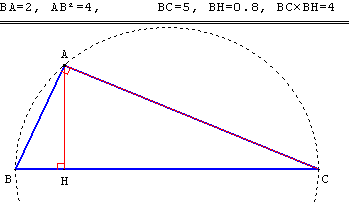
Le symétrique du point A par rapport à la perpendiculaire en B à (BC) fournit le contre-exemple de la figure ci-dessus à droite :
et sont de sens contraires, le triangle ABC est obtusangle en B, ce n'est pas un triangle rectangle.

II.7. Produit scalaire et théorème de la médiane

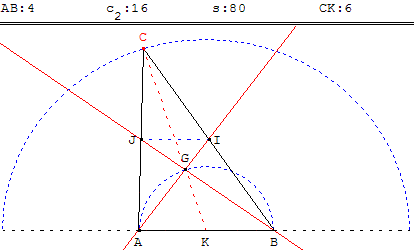
Médianes perpendiculaires

ABC est un triangle, I et J les milieux respectifs de [BC] et [AC].

En utilisant le théorème de la médiane, démontrer que :
les médianes (AI) et (BJ) sont perpendiculaires si, et seulement si, BC² + AC² = 5 AB².

Indications

D'après le théorème de la médiane, avec K milieu de [AB], on a :
CA² + CB² = 2 CK² + .

Le triangle est alors dit « orthomédian » en A et B.

Voir preuve – Classe de première : triangle

Droites perpendiculaires dans un triangle rectangle

Table des matières

Dans d'autres pages du site

Exercices résolus par produit scalaire

Produit scalaire dans l'espace

Carré d'aire 5 fois plus petite

Les problèmes du BOA : triangles et produit scalaire

Retrouver un triangle à partir de droites remarquables

Retrouver un triangle à partir de centres ou de pieds

Cercles d'Apollonius : lieu géométrique dans le triangle

Mobile friendly

Téléchargement

 Télécharger produit_scalaire.doc :

Google considère l'URL de ce document au format « .doc »comme une erreur de type "soft 404" mais référence les copies !

Télécharger produit_scalaire.pdf : ce document au format « .pdf »

Copyright 2003 - © Patrice Debart

Rétrolien (backlink)

Programmation scientifique