Descartes et les Mathématiques

Configurations fondamentales – Cercles

Le cercle, en classe de 2^nde, avec la géométrie dynamique.

Sommaire

1. Deux cercles sécants
    a. Deux diamètres de même extrémité
    b. Cercles et trapèzes

    c. Cordes parallèles - Théorème de Reim

2. Théorème de Ptolémée

3. Droites concourantes dans un quadrilatère inscrit

4. Hexagramme

5. Théorème de Clifford

   Quatre cercles de même rayon

6. Quadrilatère inscriptible orthodiagonal

7. Théorème des cinq cercles

Humeur et tableau noir – Plot n^o 25

Exemples d'exercices pouvant être résolus, en classe de 2^de, avec les configurations du plan

Savoir reconnaître les configurations de base concernant le cercle, les angles inscrits et l'inscription de l'angle droit dans un demi-cercle.

Tangentes à un cercle passant par un point donné

Paragraphe déplacé dans l'article : cercle au collège

1. Deux cercles sécants

1.a. Deux diamètres de même extrémité

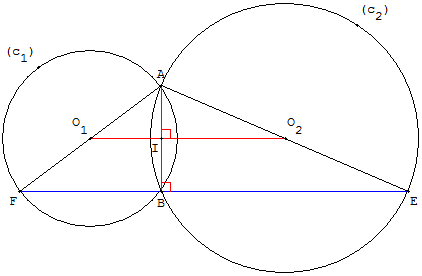
Deux cercles (c₁) et (c₂), de centres respectifs O₁ et O₂, se coupent en deux points A et B.
On trace le diamètre [AF] de (c₁) et le diamètre [AE] de (c₂).

  – Montrer que (FE) // (O₁O₂),
  – montrer que FE = 2 × O₁O₂,
  – montrer que le segment [FE] passe le point d'intersection B.

Indication

Il suffit de remarquer que la droite (O₁O₂), médiatrice de [AB], est une droite des milieux du triangle AFE.
(FE) est parallèle à (O₁O₂).

Soit I le milieu de [AB], (O₁I) est aussi une droite des milieux du triangle AFB.
(FB) et (FE) sont parallèles à (O₁O₂). Les points F, B et E sont alignés.

Télécharger la figure GéoPlan 2cer_secants.g2w

1.b. Cercles de même rayon et trapèzes

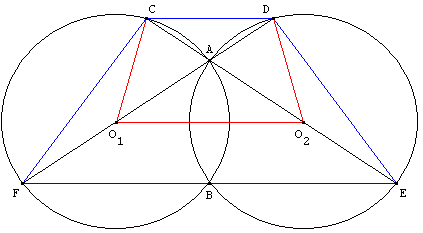
Deux cercles (c₁) et (c₂), de centres O₁ et O₂, et de même rayon sont sécants en A et B.
La droite (O₂A) recoupe (c₁) en C et (c₂) en E,
la droite (O₁A) recoupe (c₂) en D et (c₁) en F.
Montrer que les quadrilatères CDEF, O₁CDO₂ et O₁FEO₂ sont des trapèzes isocèles.

Indication

Utiliser la symétrie par rapport à la droite (AB) qui transforme (c₁) en (c₂) et (O₁A) en (O₂A).
Les points D et F ont alors pour images C et E.

Télécharger la figure GéoPlan trap_cer.g2w

1.c. Cordes parallèles - Théorème de Reim

A. Reim, géomètre sudète, 1832-1922.

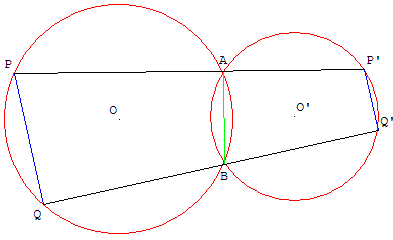
Deux cercles (c) et (c’) se coupent en A et B.

Une droite (d), passant par A, recoupe (c) en P et (c’) en P’.

Une droite (Δ), passant par B, recoupe (c) en Q et (c’) en Q’.

Montrer que les droites (PQ) et (P’Q’) sont parallèles.

Solution : calculer l'angle de droites (PQ, P’Q’)

(PQ, P’Q’) = (PQ, PP’) + (PP’, P’Q’) (π),
    = (PQ, PA) + (P’A, P’Q’) (π),
    = (BQ, BA) + (BA, BQ’) (π) angles inscrits supplémentaires dans (c) et (c’),
    = (BQ, BQ’) (π) = 0 (π).

(PQ, P’Q’) = 0 (π) d'où (PQ) et (P’Q’) sont parallèles.

Télécharger la figure GéoPlan cordes_para.g2w

2. Théorème de Ptolémée

Ptolémée

Claude Ptolémée, mathématicien, astronome et géographe grec, est né vers 85 à Ptolémaïs Hermius, a vécu à Alexandrie et mourut à Canopé vers 165.
Il est considéré comme le plus grand astronome de l'antiquité.

Son livre grande syntaxe mathématique, écrit en 140, est connu sous le nom d'Almageste. Il contient la somme des connaissances astronomiques de l'époque et a dominé l'astronomie jusqu'à Copernic (1543).

Voir pentagone régulier : construction de Ptolémée

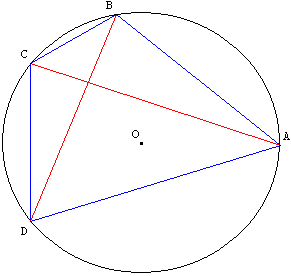
Théorème : un quadrilatère convexe est inscriptible, si et seulement si la somme des produits des côtés opposés est égale au produit des diagonales.

Avec les notations de la figure ci-dessous :

AB × CD + BC × DA = AC × BD.

Télécharger la figure GéoPlan ptolemee.g2w

Démonstration de la propriété directe utilisant les angles inscrits et les triangles semblables

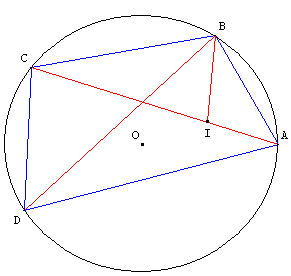
Soit I le point de [AC] tel qu'on ait l'égalité des angles : ABI = CBD.

On a BÂC = BDC comme angles inscrits interceptant la même corde [BC]. Les triangles CBD et IBA sont semblables,
CD/IA = BD/BA et AB × CD = IA × BD.

De même, on a les égalités d'angles CBI = CBD + DBI = DBI + IBA = DBA. BCA = BDA comme angles inscrits interceptant la même corde [BA].
Les triangles ABD et IBC sont semblables,
AD/IC = BD/BC et AD × BC = IC × BD.

En sommant les deux égalités, on obtient :

AB × CD + AD × BC = IA × BD + IC × BD = (AI + IC) × BD = AC × BD,

soit l'égalité de Ptolémée.

Télécharger la figure GéoPlan ptoleme2.g2w

Réciproque

Inversion : cette transformation n'est plus enseignée, mais pourrait être citée en terminale S comme contre-exemple de linéarité.

L'inversion i(I, k) de pôle I et de rapport k est la transformation du plan qui à un point M, distinct de I, fait correspondre le point M’ de la droite (IM) tel que . = k.

Entre un couple de points (M, N) et son image (M’, N’), on a : M’N’ =

Une inversion de pôle I est une involution bijective du plan privé de I dans lui-même.

L'image d'une droite ou d'un cercle, éventuellement privé du pôle I, est une droite ou un cercle, éventuellement privé du point I.

Par une inversion, l'image d'une droite ne passant par le pôle est un cercle, passant par le pôle, privé du pôle.

Démonstration de la propriété réciproque de Ptolémée utilisant l'inversion

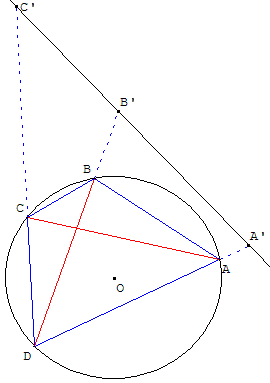
Soit quatre points A, B, C et D tels que AB × CD + BC × DA = AC × BD.

En divisant cette égalité par DA × DB × DC on a :

Une inversion de pôle D transforme A en A’, B en B’ et C en C’.
Le calcul des distances entre les points transformés A’B’ = k …
entraîne, grâce à la formule précédente : A’B’ + B’C’ = A’C’.

Les trois points A’, B’, C’ sont alignés sur une droite (d). Les images réciproques de points de la droite (d) sont situées sur un cercle (c) passant par D. Les points A, B, C et D sont donc cocycliques.

Télécharger la figure GéoPlan ptolemee_inv.g2w

3. Droites concourantes dans un quadrilatère inscrit

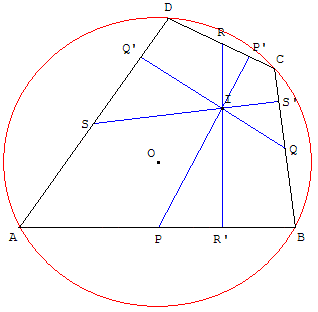
ABCD est un quadrilatère inscrit dans un cercle. P, Q, R et S sont les milieux respectifs des côtés [AB], [BC], [CD] et [DA].

P’ est la projection orthogonale de P sur (CD), Q’ est la projection orthogonale de Q sur (DA),
R’ est la projection orthogonale de R sur (AB) et S’ est la projection orthogonale de S sur (BC).

Montrer que les droites (PP’), (QQ’), (RR’) et (SS’) sont concourantes.

Indications pour la démonstration

Soit I le point d'intersection de (PP’) et (QQ’).
Montrer que 2 = + + + .

Établir la même relation pour 2 , où J est le point d'intersection de (RR’) et (SS’).
Conclure que I = J est le point de concours des quatre droites.

Télécharger la figure GéoPlan dr_concou_quadri.g2w

4. Hexagramme

4.a. Théorème de Pascal dit de l'hexagramme mystique :

Pour un hexagone inscrit dans une conique, le théorème de Pascal affirme que les points d'intersection des côtés opposés de l'hexagone, s'ils existent, sont alignés.

La droite que forme cet alignement est appelée droite de Pascal. La figure est appelée hexagramme mystique.

Télécharger la figure GéoPlan hexagramme.g2w

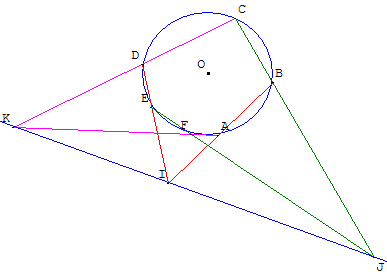
4.b. Application au cercle

ABCDEF est un hexagramme (hexagone inscriptible dans un cercle : ici le cercle de centre O, passant par A).
Les côtés opposés se coupent en I, J et K.
D'après le théorème de Pascal les points I, J et K sont alignés.
Vérifier !

À l'aide du théorème de Ménélaüs, Pascal a démontré ce théorème, puis il l'a généralisé à n'importe quelle conique, sachant que c'est une propriété projective, et qu'une propriété projective du cercle est valable pour toute conique.

4.c. Hexagramme inscrit dans le cercle d'Euler

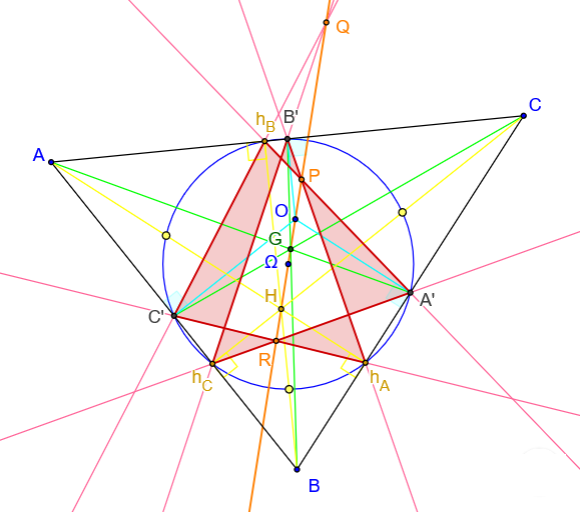
Cercle des neuf points d'Euler

Dans un triangle ABC, les points A’, B’, C’ sont les milieux des côtés
et les points h_A, h_B, h_C, sont les pieds des hauteurs.

Le cercle d'Euler passe par les neuf points suivants :
    – les trois milieux des côtés du triangle ;
    – les trois pieds des hauteurs ;
    – les trois points d’Euler ; milieux des segments [AH], [BH] et [CH] où H est l'orthocentre du triangle ABC.

(OH) est la droite d'Euler.
Le centre de gravité G est au tiers de [OH] à partir du point O, centre du cercle circonscrit .
Le centre Ω du cercle d'Euler est le milieu de [OH].

Hexagramme

Les côtés opposés de l'hexagone A’h_BC’h_AB’h_C, inscrit dans le cercle d'Euler, se coupent en P, Q et R.

La droite (PQ), droite de Pascal de l'hexagramme A’h_BC’h_AB’h_C, est la droite d'Euler du triangle ABC.

Figure interactive dans GeoGebraTube : Hexagramme inscrit dans le cercle d'Euler

5. Trois cercles de même rayon ayant un point commun

5.a. Théorème de Clifford - Orthocentre

Trois cercles de centres P, Q et R de même rayon ρ passent par un point O commun.
A, B et C sont les autres points d'intersection des cercles pris deux à deux.
Montrer que le point O est l'orthocentre du triangle ABC.

Le cercle circonscrit au triangle ABC a pour rayon ρ.
Son centre I est l'orthocentre du triangle PQR.

Les triangles ABC et PQR sont symétriques par rapport au point J milieu de [OI].

De façon duale, le centre du cercle circonscrit et l'orthocentre de l'un des triangles ABC ou PQR sont respectivement l'orthocentre et le centre du cercle circonscrit de l'autre.

Orthocentre

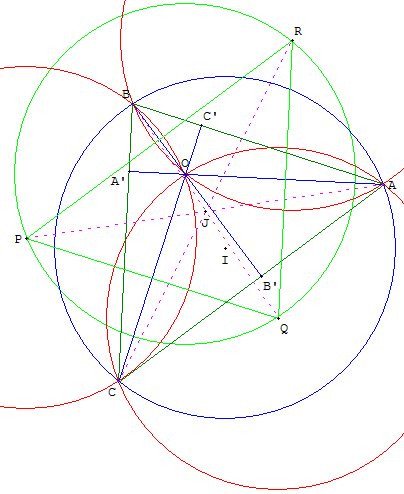
Indication : OQAR, ORBP et OPCQ sont des losanges (dont la longueur des côtés est égale au rayon ρ).

Solution vectorielle

Soit I le point tel que = , BICP est un losange.
Vu ces losanges, on a = = , donc = et RAIB est un losange et IA = IB = ρ.
Dans ce losange on a aussi = et comme = = , on a = , IAQC est un losange et IA = IC = ρ.

Le cercle de centre I et de rayon ρ passe par les points A, B et C.

Comme = , RBCQ est un parallélogramme et = .
La diagonale (AO) du losange OQAR est orthogonale à (RQ), donc à (BC) : (AO) est donc la hauteur issue de A du triangle ABC.
De même, les droites (BO) et (CO) sont des hauteurs et le point O est l'orthocentre de ABC.

On a vu que = = donc ACPR est un parallélogramme A et C sont symétriques de P et R par rapport au centre J du parallélogramme.
Les triangles ABC et PQR sont symétriques par rapport à ce point J, et comme = , J milieu de [PA] est aussi le centre du parallélogramme OPIA, donc le milieu de [OI].

Télécharger la figure GéoPlan clifford.g2w

Visualisation d'un cube en perspective

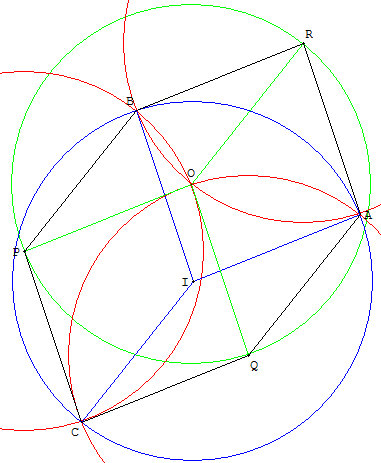
TS : Démonstration par calcul d'affixes de complexes.

Les affixes des points sont notées par les minuscules correspondantes, l'origine est en O.

OQAR, ORBP et OPCQ sont des losanges ρ, d'où : a = q + r, b = r + p et c = p + q.

Le point I d'affixe ω = p + q + r est le centre d'un cercle de rayon ρ passant par les points A, B et C car :
|ω − a| = |p| = ρ, |ω − b| = |q| = ρ et |ω − c| = |r| = ρ.

Rappel : le produit scalaire de (z) et (z’) est . = Re(z) = (z + z’)

(OA) est orthogonale à (BC), car le produit scalaire . est la partie réelle de (c − b) = ( + ) (q − r) = q − r + q − r .

Or q = r = ρ², donc (c − b) = q − r est imaginaire pur, sa partie réelle est nulle : (AO) est une hauteur du triangle ABC.
On montre, de même, que (BO) est une deuxième hauteur, donc O est l'orthocentre du triangle ABC.

= = . Le point J() est le milieu [PA]. P et A sont symétriques par rapport à J. On vérifie que Q et B, puis R et C sont symétriques par rapport à J : les triangles PQR et ABC sont symétriques par rapport au point J milieu de [OI].

Télécharger la figure GéoPlan clifford_s.g2w

Voir hauteurs et orthocentre : géométrie du triangle

Voir aussi : plan complexe

5.b. Trois cercles de même rayon - Deux autres cercles

Voici un problème de géométrie que l'on peut résoudre sans règle ni compas.
Une pièce suffira, mais c'est mieux avec GéoPlan.

Utiliser la pièce pour tracer trois cercles, passant par un même point P.
Une fois tracés, ces trois cercles se recoupent en trois autres points Q, R et S.

Cette même pièce permet-elle de tracer un quatrième cercle passant par ces trois points ?
Où le centre O de ce dernier cercle est-il situé ?

Théorème de Johnson

Roger Arthur Johnson - géomètre (1890-1954)

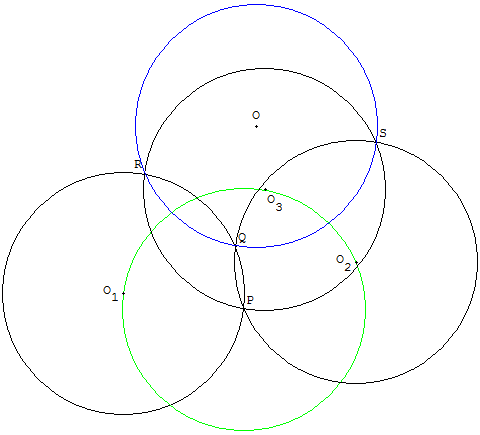
Trois cercles distincts, de même rayon r, passent par un même point P.
R, S, Q sont les deuxièmes points communs aux cercles.
Le cercle circonscrit au triangle RSQ a pour rayon r.

Deux autres cercles de même rayon

Les centres O₁, O₂, O₃, des trois cercles initiaux, sont situés sur un cercle de centre P et de rayon r.

Un cinquième cercle passant par les trois points d'intersection Q, R et S, autres que P, a la même taille que les trois premiers.
Appelons O son centre.

Télécharger la figure GéoPlan mon_534.g2w

WikiPédia : Théorème de Pohlke

Voir : utilisation de l'espace dans la résolution d'un problème plan

Autre visualisation d'un cube en perspective

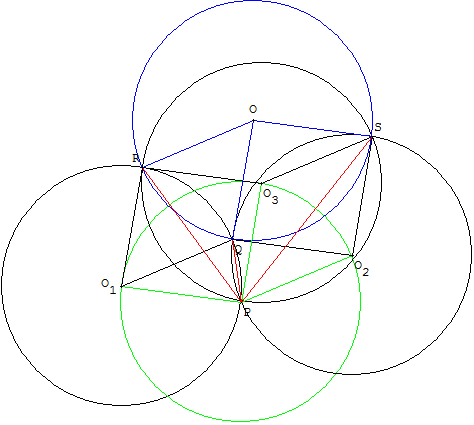
Indications

Nous remarquons tout d'abord que les quadrilatères PO₁QO₂, PO₂SO₃ et PO₁RO₃ sont des losanges de côtés de longueur r.

D'après le théorème de Pohlke, P, O₁, O₂, O₃ peuvent être considérés comme la représentation en perspective cavalière d'un coin de cube de sommet P.

Dans cette même perspective, les losanges PO₁QO₂, PO₂SO₃ et PO₁RO₃ sont trois faces de ce cube dont on « voit » 7 sommets et 9 arêtes.

Toutes ces arêtes sont de longueur r. Il en est de même des trois dernières arêtes obtenues en complétant les losanges représentant les autres faces, ce qui donne au passage la position du point O, à la distance r de Q, R et S.

O est donc le centre du cercle passant par Q, R et S, et le rayon de ce cercle est également r.

Télécharger la figure GéoPlan mon_534_b.g2w

Remarques

Si P et Q sont les points d'intersection des cercles (c₁) et (c₂), le cercle circonscrit est l'image du cercle (c₃) par la translation de vecteur .
Le centre cherché, image de O₃ par la translation, est le quatrième sommet O du parallélogramme PQO₃O.
Deux autres translations de vecteurs et permettent aussi de trouver le centre. (Les vecteurs de translation , et « sont » les diagonales des losanges issus de P.)

Orthocentres

P est l'orthocentre du triangle QRS

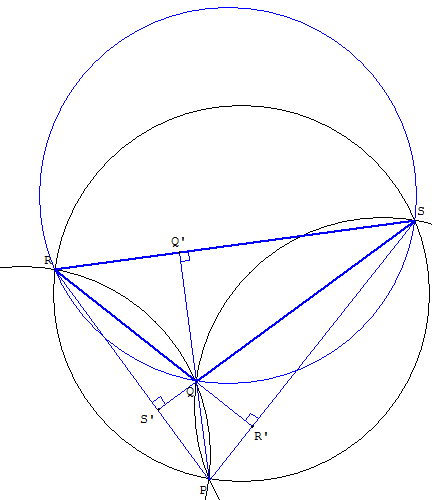
D'après le théorème de Clifford, P est l'orthocentre du triangle QRS.

Télécharger la figure GéoPlan trois_cercles.g2w

O est l'orthocentre du triangle O₁O₂O₃

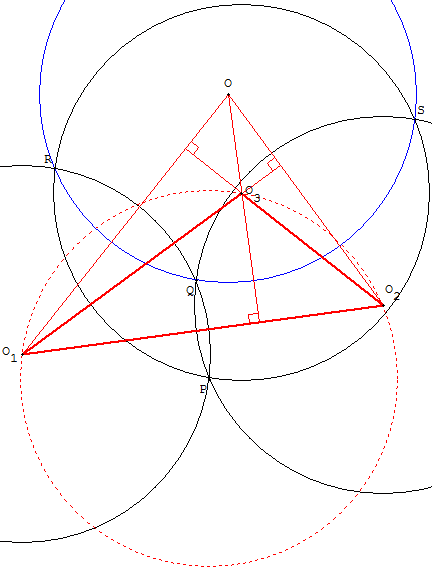
De façon duale, le centre O est l'orthocentre du triangle O₁O₂O₃ dont les sommets sont les centres des trois cercles.

6. Théorème des cinq cercles (Miquel)

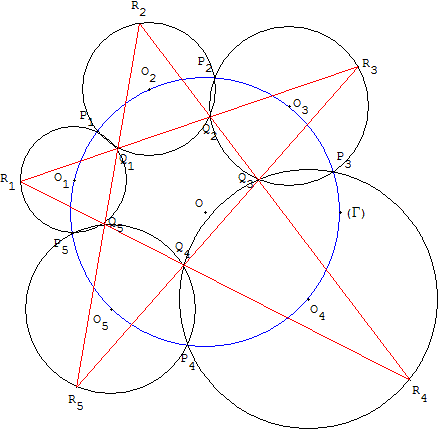
Soit une suite de cinq cercles (c₁), (c₂), (c₃), (c₄), (c₅) centrés sur un cercle (Γ) ;
tels que les cercles (c₁), (c₂), (c₃), (c₄), (c₅) coupent respectivement (c₂), (c₃), (c₄), (c₅), (c₁) en P₁, P₂, P₃, P₄, P₅ situés, dans cet ordre, sur le cercle (Γ).

Les autres points d'intersection Q₁, Q₂, Q₃, Q₄, Q₅ sont situés à l'intérieur du cercle (Γ).

Le théorème des cinq cercles affirme que les droites portées par les côtés du pentagone convexe Q₁Q₂Q₃Q₄Q₅ ont leurs points d'intersection R₁, R₂, R₃, R₄, R₅ situés sur les cinq cercles (c₁), (c₂), (c₃), (c₄), (c₅).

Télécharger la figure GéoPlan cinq_cercles.g2w

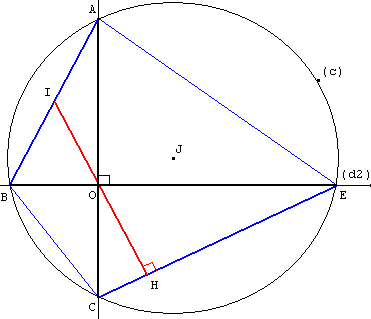
7. Quadrilatère inscriptible orthodiagonal

Classe de 2^nde

Théorème de Brahmagupta (mathématicien indien du VII^e siècle) :
si les diagonales d'un quadrilatère inscriptible sont perpendiculaires l'une à l'autre et se coupent en un point O, une droite passant par O et perpendiculaire à l'un quelconque des côtés coupe le côté opposé en son milieu.

Utiliser la propriété des angles inscrits dans la figure ci-contre.

Soit (c) un cercle de centre J, de rayon r.
O un point à l'intérieur du cercle, distinct de J.
Deux droites (d) et (d₂) orthogonales pivotent autour du point O.
La droite (d) coupe le cercle (c) en A et C, (d₂) coupe (c) en B et E.

Les points cocycliques A, B, C et E forment le quadrilatère orthodiagonal ABCE.

Soit I le milieu de la corde [AB] et H le projeté orthogonal de O sur la corde [CE].

Montrer, par calcul d'angles, que la médiane [OI] de BOA est hauteur du triangle COE :

Pour prouver que la hauteur (OH) est perpendiculaire à (CE), utiliser la propriété du triangle rectangle BOA « le milieu de l'hypoténuse est équidistant des trois sommets », d'où des triangles isocèles, puis des égalités d'angles…, jusqu'à conclure avec des angles complémentaires.

Construction à l'équerre du milieu d'une corde

Un cercle et l'une des cordes [AB] sont tracés sur une feuille de papier.
Vous ignorez où se trouve le centre du cercle, et ne disposez que d'une équerre, aux angles inconnus, mais suffisamment grande (l'un des côtés mesure au moins le diamètre du cercle).

Construire, à l'aide de cette seule équerre, le milieu de la corde.

Solution : Placer deux bords de l'équerre en A et B, tels que le sommet se trouve à l'intérieur du cercle, en un point O.
Tracer deux cordes perpendiculaires [AC] et [BE], passant par O.

Tracer la perpendiculaire à (CE) passant par O. Elle coupe [AB] en son milieu I.

Preuve : Les angles inscrits BAC et BEC sont égaux. BEC est aussi égal à COH (ils ont un complémentaire commun HCO) et à IOA (opposé par le sommet au précédent).
Il en résulte que dans le triangle isocèle AOI, AI = IO.

Avec le même raisonnement, on obtient l'égalité angulaire ABE = ACE = EOH = IOB.
Dans le triangle isocèle BOI, BI = IO.

AI = IO = BI, le point I est bien le milieu de [AB].

Télécharger la figure GéoPlan qua_insc_boa.g2w

Quadrilatère orthodiagonal, voir : produit scalaire, aire du quadrilatère orthodiagonal

Table des matières

Dans d'autres pages du site

Le cercle au collège

Théorème des trois cercles : voir théorème du pivot (premier théorème de Miquel)

Cercles orthogonaux, axe radical et faisceau de cercles : voir géométrie du cercle

Théorème de Descartes - Cercles de Soddy

Trois cercles égaux tangents à l'intérieur d'un triangle

Figure interactive avec GeoGebra :
    puissance d'un point par rapport à un cercle

Problèmes de contact

Définition : tangentes à un cercle
    – en un point du cercle (quatrième)
    – passant par un point donné (troisième-seconde)

Tangentes communes à deux cercles : collège – lycée

Cercle tangent à deux droites, passant par un point donné :
    collège – problème de contact PDD – homothétie

Cercle passant par trois points

Cercle tangent à trois droites

Cercles tangents à des droites ou à des cercles : problèmes de contact

Mobile friendly

Téléchargement

 Télécharger cercle seconde.doc,
Google considère l'URL de ce document au format « .doc »comme une erreur de type "soft 404", mais référence les copies !

Télécharger cercle_seconde.pdf : ce document au format « .pdf » d'Adobe Acrobat

Copie sur d'autres sites avec cookies et publicités

studylibfr.com/configurations-fondamentales

Copyright 2003 - © Patrice Debart