Descartes et les Mathématiques
Théorème de Descartes - Cercles de Soddy
Cas particulier du problème des trois cercles d'Apollonius
Sommaire
1. Cercles tangents à 3 cercles tangents deux à deux
3. Cercles tangents à une droite et à 2 cercles tangents entre eux et tangents à la droite
Deux théorèmes sont nommés théorème de Descartes
• Un, en algèbre, pour déterminer le nombre de solutions d'une équation :
Une variation d'un polynôme est un changement de signe entre deux termes consécutifs.
Théorème de Descartes pour les équations :
Dans une équation algébrique, à coefficients réels, le nombre des racines positives ne surpasse pas le nombre de variations ; et, quand il est moindre, la différence est toujours un nombre pair.
• Un théorème de Descartes en géométrie
Ci-dessous, ce théorème, découvert par René Descartes en 1643, qui établit une relation entre les rayons de quatre cercles tangents entre eux.
1. Cercles tangents à trois cercles tangents deux à deux
3 cercles inscrits dans un cercle - Cercle tangent à trois cercles donnés
Trois cercles tangents deux à deux étant donnés, il existe deux cercles qui leur sont tangents : ce sont les cercles de Soddy.
Trois cercles tangents et deux cercles de Soddy
Sangaku
Construction en géométrie synthétique
a) À partir de deux points O1 et O2, construction de deux cercles (c1), (c2) tangents extérieurement en T, puis d'un troisième cercle (c3) tangent en U,
b) puis avec deux cercles auxiliaires, construction des deux cercles de Soddy, de centres O4 et O5, tangents aux trois cercles tangents (c1), (c2) et (c3).
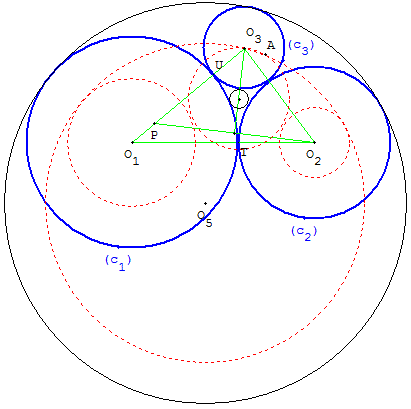
a) On donne deux points O1 et O2 et un point T du segment [O1O2] plus près de O2 que de O1.
On trace les cercles (c1), (c2) de centres O1, O2 ; de rayons r1 = O1T et r2 = O2T.
On choisit un point U sur le cercle (c1) et à partir de ce point U, en reportant le rayon r2 sur [UO1], on place le point P tel que UP = r2. La médiatrice de [PO2] coupe la droite (O1U) en O3 qui est le centre du cercle (c3) passant par U, de rayon r3 = O3U, tangent à (c1) et à (c2).
b) Quitte à renommer les cercles on suppose que r1 > r2 > r3 et on trouve deux solutions avec la première construction CCC du problème d'Apollonius grâce à deux cercles auxiliaires de centres O1, O2 ; de rayons r1– r3, r2– r3.
Pour cela trouver le point A, image de O3 par l'homothétie qui transforme les cercles auxiliaires, avec O2 image de O1.
Il suffit de tracer les cercles tangents à un de ces cercles auxiliaires, passant par O3 et A.
Les centres O4 et O5 sont les centres des cercles solutions. Il suffit alors de diminuer ou d'augmenter les rayons de r3 pour trouver les deux solutions.
Télécharger la figure GéoPlan 4cercles_Descartes.g2w
2. Théorème de Descartes
Expression clé : cercles de Descartes
en : Descartes Circle Theorem
Calcul des rayons de deux cercles tangents, dans le cas particulier du problème des trois cercles d'Apollonius, cas où les 3 cercles sont tangents deux à deux.
Dans la configuration de la figure ci-dessus, étant donné trois cercles tangents deux à deux extérieurement, on peut trouver deux cercles (c4) et (c5) tels que,
si k1 = 1/r1, k2 = 1/r2, k3 = 1/r3, k4 = 1/r4 et k5 = 1/r5 sont les inverses des rayons des cinq cercles, on ait les relations suivantes :
Cercle (c4) tangent extérieurement à (c1), (c2) et (c3)
(k1 + k2 + k3 + k4)2 = 2(k12 + k22 + k32+ k42)
(k1 + k2 + k3 – k4)2 = 4(k1k2 + k2k3 + k1k3) ;
d'où le calcul de la courbure :
k4 = (k1 + k2 + k3) + 2rac(k1k2 + k2k3 + k1k3) et du rayon r4 = 1/k4 ;
on trouve le centre O4 en choisissant la bonne intersection du cercle de centre O1 et de rayon r1+ r4 avec le cercle centre O2 et de rayon r2 + r4 ;
Cercle (c5) tangent intérieurement à (c1), (c2) et (c3)
(k1 + k2 + k4 – k5)2 = 2(k12 + k22 + k42+ k52)
(k1 + k2 + k3 + k5)2 = 4(k1k2 + k2k3 + k1k3) ;
d'où k5 = − (k1 + k2 + k3) + 2rac(k1k2 + k2k3 + k1k3) et r5 = 1/k5 ;
on trouve le centre O5 à une des intersections du cercle de centre O1 et de rayon r5 – r1 avec le cercle centre O2 et de rayon r5 – r2.
Ces formules se généralisent à quatre cercles quelconques, tangents deux à deux, en appelant courbure l'inverse du rayon.
Pour un cercle donné, la courbure est positive si au moins un des autres cercles lui est tangent extérieurement,
elle est négative si les trois autres cercles lui sont tangents intérieurement.
La formule de Descartes, découverte en 1643, établit la relation
(k1 + k2 + k3 + k4)2 = 2(k12 + k22 + k32+ k42)
entre les courbures de quatre cercles tangents entre eux.
Voir WikiPédia : Théorème de Descartes
Démonstration du théorème de Descartes de Philip Beecroft (1842) :
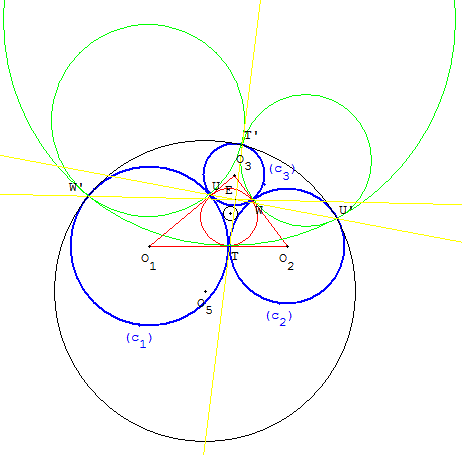
si U, T, W sont les points de contact entre les cercles (c1), (c2) et (c3), le cercle circonscrit à UTW est inscrit dans le triangle O1O2O3. Si U’, T’, W’ sont les points de contact des cercles (c1), (c2) et (c3) avec le cercle (c5), la démonstration se fait par le calcul des rayons des cercles circonscrits à UT’W’, U’TW’, U’T’W.
Les droites (UU’), (TT’) et (WW’) sont concourantes au point E, premier point d'Eppstein (2001).
Les centres O4 et O5 sont les points de Soddy du triangle O1O2O3.
Télécharger la figure GéoPlan 4cercles_demonstration.g2w
Géométrie analytique
Ces formules peuvent être utilisées pour construire les deux cercles de Soddy, tangents à trois autres.
Cercles donnés tangents extérieurement
Étant donné deux points O1, O2, et trois rayons r1, r2, r3 tels que r1 > r2 > r3 ;
on trouve le point O3 à une des intersections du cercle de centre O1 et de rayon r1 + r3 avec le cercle centre O2 et de rayon r2 + r3.
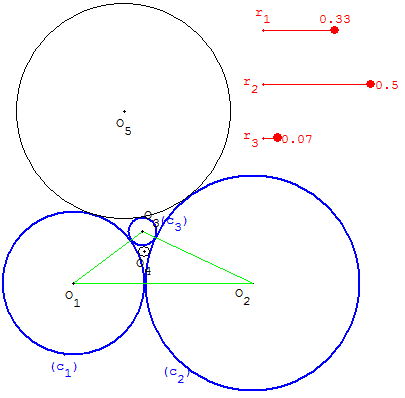
Exemple avec k1 = 3, k2 =2, k3 = 15. On trouve k4 = 38 et k5 = 12.
Remarque GéoPlan : la première figure du théorème de Descartes est construite en ajoutant r3 au rayon du cercle auxiliaire de centre O5. Cela permet de trouver le cercle (c5) tangent intérieurement aux trois autres.
Lorsque r3 est très petit, le cercle (c5) est tangent extérieurement et on le trouve en modifiant la construction pour enlever r5 au rayon du cercle auxiliaire.
La figure ci-dessus n'en fait qu'une pour traiter ces deux cas et en plus le cas ci-contre.
Cercles (c2) et (c3) tangents intérieurement à (c1)
Sangaku
Exemple avec k1 = −6, k2 = 10, k3 = 19.
On trouve k4 = 31 et k5 = 15.
Lorsque (c2) et (c3) sont tangents intérieurement à (c1), la construction géométrique n'est pas évidente (je ne sais pas caractériser le point A dans ce cas).
La figure de géométrie analytique donne les deux solutions.
Télécharger la figure GéoPlan 4cercles_analytique.g2w
3. Cercles de Soddy particuliers
Sangaku : cercles tangents à une droite et à deux cercles tangents entre eux et tangents à la droite
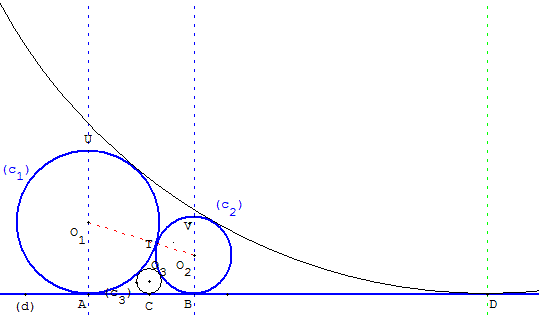
Soit deux points A et B situés sur une droite (d), un point O1 sur la perpendiculaire en A à (d).
Le cercle (c1) de centres O1, de rayon r1 et de diamètre [AU] est tangent en A à (d).
La droite (UB) recoupe le cercle (c1) au point T. La perpendiculaire à (d) en B coupe la droite (O1T) au point O2 qui est le centre d'un cercle (c2) passant par T, de rayon r2 = O3U, tangent à (c1) en T et à (d) en B.
Justification (figure de droite) : l'homothétie de centre T qui transforme U en B, transforme la droite (AU), perpendiculaire à (d), en une droite parallèle : la perpendiculaire à (d) en B. Les images de O1 et A sont alignées avec T et situées sur cette dernière perpendiculaire : ce sont les points O2 et V. Le cercle (c1) de diamètre [AU] a pour image le cercle (c2) de diamètre [VB]. Ces deux cercles ayant en commun l'unique point T sont tangents en T.
La tangente en U à (c1) parallèle à (d) a pour image une tangente parallèle passant par B : c'est la droite (d) et donc (c2) est aussi tangent en B à (d).
Télécharger la figure GéoPlan 3cercles_Descartes.g2w
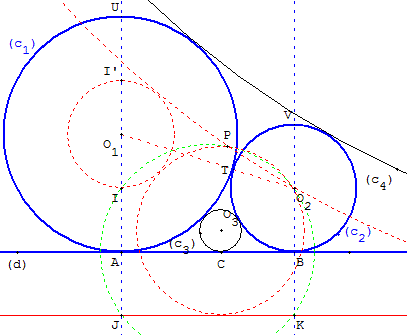
Quitte à renommer les cercles on suppose que r1 > r2 et on trouve deux solutions avec la construction du problème de contact CCD.
Pour cela, avec la « méthode de Viète, des translations parallèles », substituer au cercle (c1) le cercle de diamètre [II’] de centre O1, de rayon r1– r2.
Soit J et K les symétriques de I et O2 par rapport à (d), substituer à (d) la droite (JK) située à une distance r2 de (d).
Le cercle circonscrit à O2IJ coupe la droite (O2I’) en P.
On se trouve dans le cas du problème de contact PDD : tracer un cercle passant par P et O2 tangent à la droite (JK) ;
on trouve deux cercles, tangents au cercle de diamètre [II’] de centres O3 et O4.
En diminuant les rayons de r2, on trouve les solutions : le cercle (c3) de centre O3 et le cercle (c4) de centre O4.
Théorème de Descartes pour deux cercles et une droite
Soit k1 = 1/r1, k2 = 1/r2, k3 = 1/r3 et k4 = 1/r4 la courbure des quatre cercles, la courbure de la droite étant nulle.
Cercle (c3) tangent à (c1), (c2) et (d)
(k1 + k2 + k3)2 = 2(k12 + k22 + k32)
(k1 + k2 – k3)2 = 4k1k2 ;
on a donc 1/rac(r3) = 1/rac(r1) + 1/rac(r2).
Cercle (c4) tangent à (c1), (c2) et (d)
(k1 + k2 + k4)2 = 2(k12+ k22 + k42)
(k1 + k2 – k4)2 = 4k1k2 ;
on a donc 1/rac(r4) = 1/rac(r2) – 1/rac(r1).
Théorème de Pythagore
Calcul des carrés des longueurs des hypoténuses [O1O2], [O1O3] et [O2O3] des triangles rectangles dont les petits côtés sont parallèles ou perpendiculaires à (d).
AB2 + (r1– r2)2 = (r1 + r2)2 d'où AB2 = 4r1r2 et AB = 2rac(r1r2).
Si C est la projection de O3 sur (d) on a AC2 + (r1– r3)2 = (r1 + r3)2 d'où AC2 = 4r1r3 et AC = 2rac(r1r3)
et CB2 + (r2– r3)2 = (r2 + r3)2 d'où CB2 = 4r2r3 et CB = 2rac(r2r3).
Comme AB = AC + CB en divisant par 2rac(r1r2r3), on retrouve 1/rac(r3) = 1/rac(r1) +1/rac(r2).
Même démonstration avec (c4), sachant que AB = AD – BD (cas de la figure ci-dessus).
4. Sangaku : kissing circles
Une infinité de cercles tangents, quatre à quatre, que Soddy a appelé « kissing circles ».
Les nombres indiqués sur les disques sont les courbures.
Trois cercles étant donnés, il existe deux cercles de Soddy qui leur sont tangents.
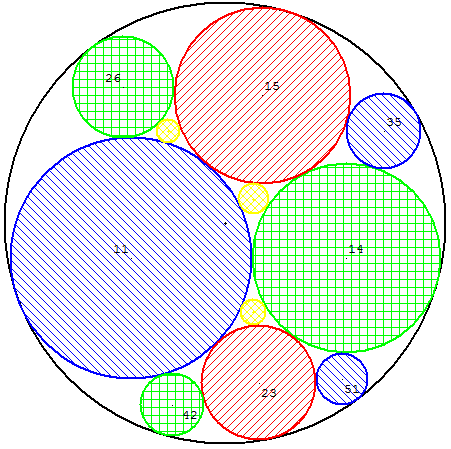
On commence avec les courbures (–6, 11, 14).
La formule de Descartes donne 15 et 23.
On continue avec (–6, 11, 15).
On retrouve 14 et un nouveau cercle de courbure 26.
Et ainsi de suite, on trouve des cercles dont toutes les courbures sont des entiers.
Télécharger la figure GéoPlan soddy_14_11.g2w
Table des matières
Dans d'autres pages du site
Rétrolien (backlink)
Apollonius sur le site de Serge Mehl
Imagr reprise dans Pinterest
Google friendly
Page no 121, créée le 19/6/2008