 Descartes et les Mathématiques
Descartes et les Mathématiques
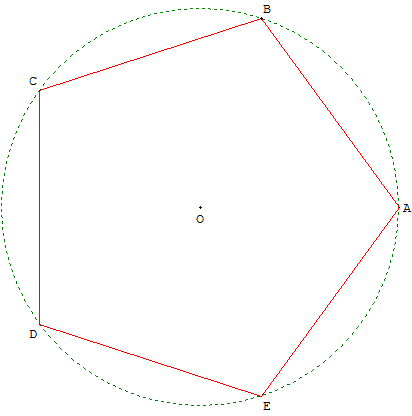
Construire un pentagone régulier
Treize méthodes de construction du pentagone à la « règle et au compas ».
Sommaire
Propriétés du pentagone (géométrie)
Dessiner un pentagone régulier à partir d'un sommet
1. Constructions de Ptolémée
2. Pentagone étoilé ou pentagramme
Découpage des pentagones en triangles d'or et d'argent
3. Construction du R.P. Durand
4. Méthode des tangentes à un cercle
6. Méthode des cercles tangents
Constructions à partir d'une diagonale
7. Construction d'Euclide
8. À partir de la longueur d'un côté situé sur une diagonale
Constructions à partir d'un côté
9. Triangle d'or et côtés consécutifs d'un pentagone
10. Construction à partir d'un carré inscrit dans un demi-cercle
Propriétés du pentagone régulier
Mesure des angles du pentagone :
l'angle au centre du pentagone régulier est de 72° et l'angle intérieur de 108°.
Angles, côté et diagonale
Longueurs du côté et de la diagonale du pentagone
Si a est la longueur du côté, d la longueur d'une diagonale
et r le rayon du cercle circonscrit, on a montré dans la page polygones réguliers
que : a = 2 r sin 36° = ![]()
![]() = r
= r ![]() ≈ 1,176 r ;
≈ 1,176 r ;
Le rapport ![]() est égal au nombre d'or φ =
est égal au nombre d'or φ = ![]() : d = a φ.
: d = a φ.
d = ![]()
![]() = r
= r ![]() ≈ 1,902 r.
≈ 1,902 r.
C'est Hippase de Métaponte, mathématicien de l'école pythagoricienne,
qui aurait découvert l'incommensurabilité de la diagonale
au côté du pentagone régulier, ainsi que la construction de cette figure.
![]() Figure interactive dans GeoGebraTube : pentagone régulier
Figure interactive dans GeoGebraTube : pentagone régulier
Méthodes de construction d'un pentagone régulier
Pour dessiner un pentagone régulier convexe,
à la « règle et au compas », on peut se donner :
• Le centre O du cercle circonscrit et un sommet A
(cinq premières constructions du pentagone régulier dans un cercle).
• Une diagonale (côté du pentagone croisé)
en choisissant deux sommets non consécutifs.
• Un côté en choisissant deux sommets consécutifs A et B.
Comment tracer un pentagone à partir d'un sommet
Construction d'un pentagone régulier inscrit dans un cercle,
à partir du centre O de ce cercle circonscrit et d'un sommet A.
Pour dessiner un pentagone régulier convexe inscrit dans un
cercle à la « règle et au compas » il suffit de savoir construire
un angle au centre de ![]() dont le cosinus est égal à
dont le cosinus est égal à ![]() .
.
Cette construction, avec le triangle rectangle de côtés
proportionnels à 1, ![]() et
et ![]() , est utilisé depuis l'antiquité
, est utilisé depuis l'antiquité
pour le tracé de sections dorées.
Le cercle de « Ptolémée » permet alors le report d'un sommet
en un point qui partage le rayon en « moyenne raison ».
1. Construction de Ptolémée du pentagone régulier
Construire un pentagone dans un cercle
Construction dite de Ptolémée ; Alexandrie 85-165 après J.-C.
À partir de l'extrémité d'un diamètre du cercle
Construction à partir d'un sommet A, situé à
l'extrémité d'un diamètre du cercle circonscrit
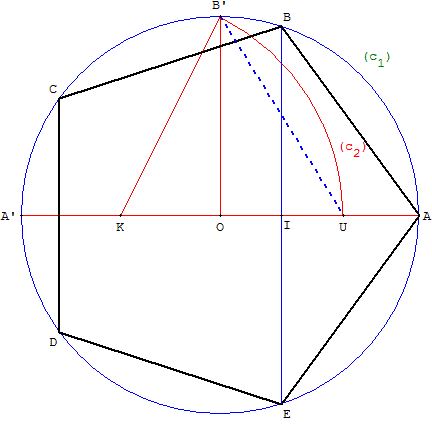
Tracer un cercle (c1) de centre O, passant par A.
On choisira comme unité le rayon du cercle.
Placer un diamètre [AA’] et un rayon [OB’], perpendiculaire à [AA’].
K est le milieu de [OA’],
le cercle de « Ptolémée » (c2) de centre K et de rayon KB’ coupe [OA] en U.
![]() =
= ![]() : le point U partage le rayon [OA] en moyenne raison.
: le point U partage le rayon [OA] en moyenne raison.
La longueur du côté du pentagone est égale à B’U.
La médiatrice de [OU] coupe le premier cercle
(c1) aux points B et E qui sont deux sommets du pentagone.
Le cercle de centre B passant par A recoupe (c1) en C.
Le symétrique D de C par rapport à (AA’) termine
la construction du pentagone.
La corde [AB] est donc le premier côté du pentagone
régulier convexe ABCDE. [EB] est un côté du
pentagone étoilé EBDAC inscrit dans le même cercle.
Calcul dans le cercle unité
En effet avec OA = 1,
le rayon du cercle de « Ptolémée » (c2) est :
KB’ = KU = ![]() d'après la propriété de Pythagore,
d'après la propriété de Pythagore,
dans le triangle OKB’ rectangle en O,
donc OU = ![]() −
− ![]() =
= ![]() et OI =
et OI = ![]() .
.
L'angle (![]() ,
, ![]() ) a un cosinus égal à
) a un cosinus égal à ![]() ,
,
c'est bien un angle de ![]() radians (72°).
radians (72°).
Remarque : Cette construction permet de tracer
un angle de 36° au compas ; AA’B = ADB = 36°.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
Construction de Ptolémée du pentagone
Sommet sur un rayon perpendiculaire
à un diamètre du cercle
Construction à partir d'un sommet A,
situé à l'extrémité d'un diamètre du cercle circonscrit
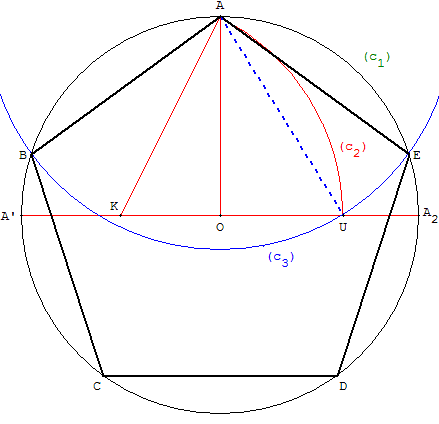
Placer les points O et A,
tracer le cercle (c1) de centre O, passant par A.
Sur un diamètre [A’A2] perpendiculaire au rayon [OA],
placer le point K au milieu de [OA’].
Dessiner le cercle de « Ptolémée » (c2) de centre K passant par A.
Ce cercle coupe le segment [OA2] en U.
Le point U partage le rayon [OA2] en « moyenne raison ».
AU est égal à la longueur du côté d'un pentagone,
inscrit dans le cercle (c1).
Tracer le cercle (c3) de centre A,
passant par U.
Ce cercle (c3) coupe (c1) aux
sommets B et E du pentagone.
Terminer la construction
du pentagone régulier par
report de la longueur
du côté
(dernière ouverture du compas).
![]() Figure interactive
Figure interactive
dans GeoGebraTube :
construction de Ptolémée
du pentagone
Figure copiée par pinterest : Construction du pentagone régulier
Ci-dessus : image du traité d'architecture
civile et militaire, R.P. Durand - 1700
Figure copiée par pinterest : Traité d'architecture civile et militaire
Remarque 1 : A’U = A’K + KU = ![]() +
+ ![]() = φ.
= φ.
Remarque 2 : OAB est un triangle isocèle d'angle au
sommet ![]() ,
les deux autres angles étant égaux à
,
les deux autres angles étant égaux à ![]() .
.
Dans le triangle IAB rectangle en I,
IB = AB cos ![]() =
= ![]() AB
AB
et EB = 2 IB = ![]() AB.
AB.
Le rapport ![]() d'une diagonale sur le côté du pentagone
d'une diagonale sur le côté du pentagone
convexe régulier est égal au nombre d'or φ.
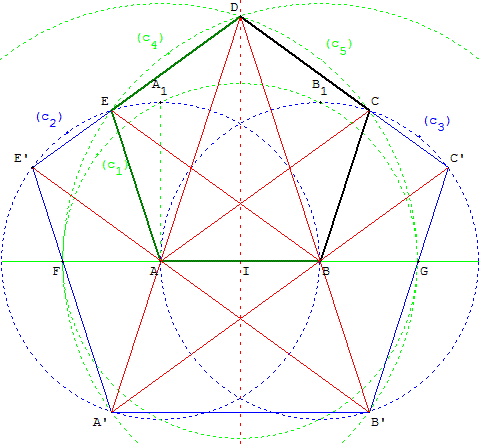
2.a. Étoile des géomètres
Construction de Ptolémée du pentagramme:
étoile à 5 branches
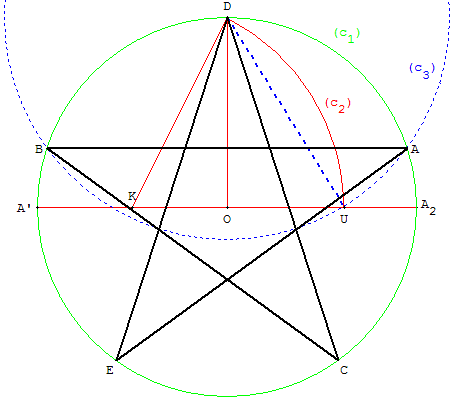
Dans un cercle (c1) de centre O, passant par un point D,
inscrire un pentagone régulier croisé, ayant pour sommet ce point D.
À partir du rayon [OD] et du diamètre perpendiculaire [A’A2],
tracer le cercle de Ptolémée (c2) passant par D, de centre K,
le milieu de [OA’]. Ce cercle coupe [OA2] en U.
Tracer le cercle (c3) de centre D, passant par U.
Les points d'intersection des cercles (c1) et (c3)
déterminent le côté [AB].
À partir de D, reporter la longueur AB pour tracer
les deux autres sommets C et E sur le cercle (c1).
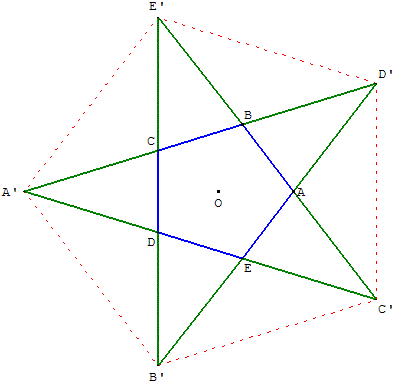
Pentagramme mystique ou pentalpha

Dans la figure ci-contre à droite,
les points A’, C’, E’, B’, D’,
nommés dans cet ordre,
sont les sommets d'un polygone
régulier étoilé appelé pentagramme.
Ce pentagramme de Pythagore
était le sceau secret de
reconnaissance des pythagoriciens,
qui y voyaient le signe de
l'harmonie et de la perfection.
Inscrit dans un cercle, le pentagramme est nommé pentacle.
2.b. Pentagone étoilé : sections d'or
Dans l'étoile à cinq branches ci-dessous,
E’A est égal à la longueur
du côté E’D’ du pentagone convexe A’B’C’D’E’
qui enveloppe le pentagramme A’C’E’B’D’.
![]() = φ. Le point A partage le côté [E’C’]
= φ. Le point A partage le côté [E’C’]
en « moyenne raison ».
Dans un pentagone convexe, la longueur d'un côté
partage la diagonale en « moyenne raison ».
Mais φ = ![]() =
= ![]() = 1 +
= 1 + ![]() ,
donc
,
donc ![]() = φ − 1 =
= φ − 1 = ![]() .
.
De même ![]() =
= ![]() .
.
![]() =
= ![]() = φ.
= φ.
Les points B et C’ partagent [E’A] en « moyenne et extrême raison ».
![]() Figure interactive dans GeoGebraTube : pentagramme étoilé
Figure interactive dans GeoGebraTube : pentagramme étoilé
Mathématiques amusantes
Un jardinier plante 10 arbres, il réalise 5 rangs de 4 arbres.
Quelle est la disposition ?
2.c. Découpage des pentagones
en triangles d'or et d'argent
Soit ABCDE un pentagone régulier, de côtés de longueur 1.
Découpage du pentagone d'or
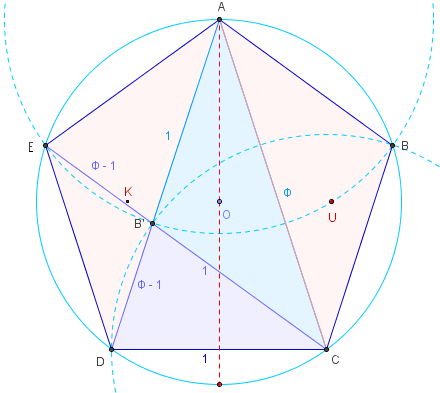
Les diagonales [AC] et [AD] partagent le pentagone
régulier en trois triangles isocèles :
deux triangles d'argent BAC et EAC de côtés de
longueurs 1, 1 et φ, d'angles ![]() et
et ![]() ;
;
un triangle d'or ACD de côtés φ, φ et 1, d'angles ![]() et
et ![]() .
.
Cette construction de triangles d'or et d'argent
est appelée pentagone d'or.
En examinant la diagonale (CE), ce triangle d'or
se décompose lui-même en un triangle d'or AB’D
de côtés 1, 1 et φ – 1 et le triangle d'argent AB’C.
De même, cette diagonale partage le triangle
d'argent EAC en deux triangles d'or AEB’ et
d'argent B’ED, aux côtés 1 et φ – 1.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
découpage du pentagone
Figure exportée dans pinterest
Découpage du pentagone croisé
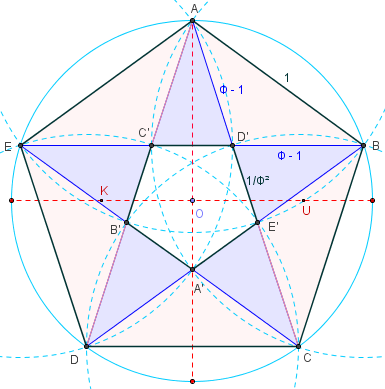
Le pentagramme ACEBD, de côtés de longueur φ,
se décompose en un petit pentagone régulier
A’B’C’D’E’ de côtés de longueur ![]() = 2 – φ ;
= 2 – φ ;
bordé par cinq triangles d'or, de côtés φ – 1, φ – 1 et ![]() .
.
En complétant le pentagone croisé par cinq triangles d'argent ;
de côtés φ – 1, φ – 1 et 1 ; on obtient le pentagone
régulier ABCDE, aux côtés de longueur 1.
Cette figure, formée par les deux pentagones
croisé et régulier, est nommée pentacle.
![]() Figure interactive dans GeoGebraTube : pentacle
Figure interactive dans GeoGebraTube : pentacle
Copie par pinterest : découpage du pentagone en triangles d'or et d'argent
Le triangle d'or ACD est utilisé par Euclide
pour la construction du pentagone régulier.
Pentagramme d'Hipassse de Métaponte
Les diagonales d'un pentagone régulier forment
un nouveau pentagone régulier, et ainsi de suite.
La méthode des soustractions entre les diagonales
et les côtés du pentagone régulier peut continuer l'infini.
Ces segments sont doc incommensurables.
Un autre pentagone croisé A’C’E’B’D’
de côtés de longueur φ – 1
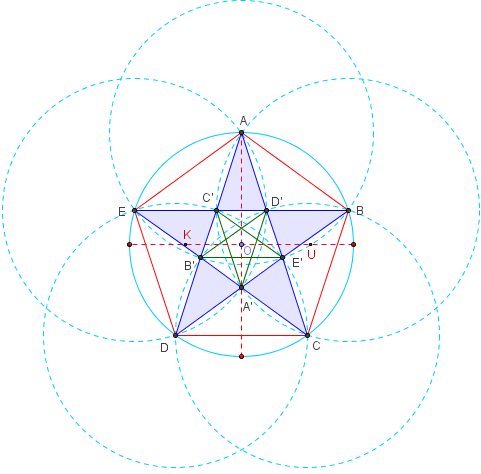
Dans un pentagone régulier ABCDE, de côtés
de longueur 1, on inscrit un pentagone croisé ACEBD.
Les intersections des côtés déterminent un petit
pentagone régulier A’B’C’D’E’ de côtés de longueur ![]() .
.
Dans ce pentagone, on inscrit un autre pentagone
croisé A’C’E’B’D’ de côtés φ – 1.
Et ainsi de suite…
![]() Figure interactive dans GeoGebraTube : pentagramme
Figure interactive dans GeoGebraTube : pentagramme
3. Construction du R.P. Durand
Variante de la construction de Ptolémée
Comment dessiner un pentagone inscrit dans un cercle
Construction à partir du centre O du cercle circonscrit et d'un sommet A.
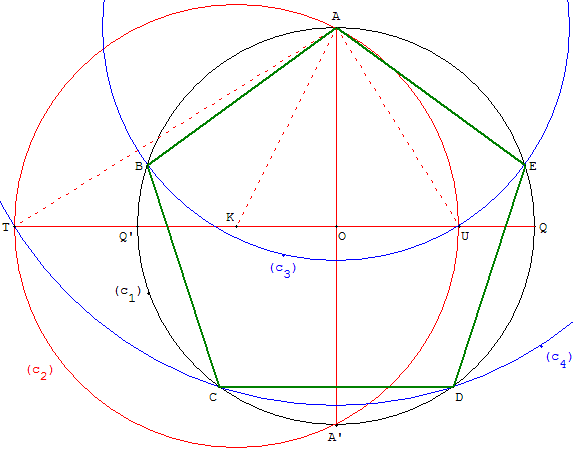
Dans la construction de Ptolémée, ci-dessus à droite,
le cercle de « Ptolémée » de centre K passant par A coupe [OQ] en U.
Le cercle de centre A passant par U permet de trouver les sommets B et E.
Avec le deuxième point T d'intersection du cercle de « Ptolémée »
et de la droite (OQ), on trace le cercle de centre A passant par T
qui permet de trouver les deux derniers sommets C et D.
Construction
Placer les points O et A, tracer le cercle (c1) de centre O,
passant par A.
Sur un rayon [OQ’], perpendiculaire au rayon [OA],
placer le point K au milieu de ce rayon.
Tracer le cercle de « Ptolémée » (c2), de centre K
passant par A. Ce cercle coupe la droite (OK) en U et T.
AU est égal à la longueur du côté d'un
pentagone convexe inscrit dans le cercle (c1),
AT est égal à la longueur du côté du pentagone croisé.
Tracer les cercles (c3) et (c4) de centre A, passant par U et T.
Le cercle (c3) coupe (c1) en B et E.
Le cercle (c4) coupe (c1) en C et D.
ABCDE est un pentagone régulier.
Remarque : avec OA = 1; alors le rayon de (c2) est ![]() ;
;
OU = ![]() ; OT = φ.
; OT = φ.
4. Méthode des tangentes à un cercle
Dessiner un pentagone régulier inscrit dans un cercle
de centre O, à partir d'un sommet A situé sur le cercle.
Méthode
Construction de deux tangentes au cercle de
diamètre [IJ], homothétique du cercle de Ptolémée
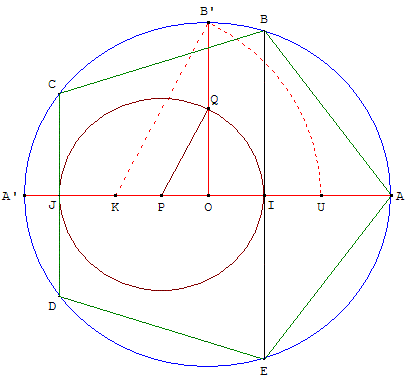
Construire la longueur ![]() comme l'hypoténuse
comme l'hypoténuse
d'un triangle rectangle ayant pour petits côtés ![]() et
et ![]() .
.
Le cercle (c3), homothétique du cercle de Ptolémée (c2),
par l'homothétie de centre O et de rapport ![]() , permet
, permet
de reporter cette longueur PQ en PI.
Les tangentes en I et J au cercle (c3), de centre P
et passant par Q, rencontrent le cercle circonscrit
en quatre des sommets du pentagone.
Construction
Tracer un cercle (c1) de centre O, passant par A.
Placer un diamètre [AA’] et un rayon [OB’],
perpendiculaire à [AA’].
P est au quart de [OA’] à partir de O : OP = ![]()
OA’ et Q est le milieu de [OB’], le cercle (c3)
de centre P et passant par Q coupe [OA] en I et [OA’] en J.
La perpendiculaire en I à (AA’) coupe le cercle (c1) en B et E.
La perpendiculaire en J à (AA’) coupe le cercle (c1)
en C et D (placés suivant la figure).
ABCDE est un pentagone régulier.
Démonstration utilisant le produit scalaire (classe de 1ère S) :
pour le prouver il suffit démontrer que AOB = 72° et AOC = 144°.
On choisira comme unité le rayon du cercle circonscrit (c1).
Dans le triangle rectangle OPQ, le théorème de Pythagore permet de trouver :
PQ = ![]() et OI = PI − PO = PQ −
et OI = PI − PO = PQ − ![]() =
= ![]() .
.
I étant la projection orthogonale de B sur (OA),
on trouve l'égalité des produits scalaires :
![]() .
.![]() =
= ![]() .
.![]() =
1 × OI =
=
1 × OI = ![]() .
.
Ce produit scalaire s'exprime en fonction de l'angle des vecteurs :
![]() .
.![]() = OA × OB cos(AOB) = 1 × 1 × cos(AOB) =
= OA × OB cos(AOB) = 1 × 1 × cos(AOB) = ![]() ,
,
donc cos(AOB) = ![]() ; AOB = 72°.
; AOB = 72°.
De même, OJ = OP + PJ = ![]() + PQ =
+ PQ = ![]() .
.
J étant la projection orthogonale de C sur (OA), on a :
![]() .
.![]() =
= ![]() .
.![]() = −1 × OJ = −
= −1 × OJ = − ![]() ,
,
et en fonction de l'angle des vecteurs :
![]() .
.![]() = OA × OC cos(AOC) = 1 × 1 × cos(AOC) = −
= OA × OC cos(AOC) = 1 × 1 × cos(AOC) = − ![]() ,
,
donc cos(AOC) = − ![]() ;
;
la formule de duplication cos(2x) = 2cos2x − 1 permet,
en vérifiant que 2 cos2 72° − 1 = − ![]() , de déduire que AOC = 144°.
, de déduire que AOC = 144°.
Les points D et E étant les symétriques de C et B par rapport à (OA),
on a donc AOD = 144° et AOE = 72°,
la figure est bien un pentagone régulier.
Démonstration utilisant les nombres complexes (Terminale S)
Dans le plan complexe choisira le centre du pentagone
comme origine O et pour le sommet A, le point d'affixe 1.
Pour le prouver il suffit démontrer que les affixes des
sommets sont les racines cinquièmes de l'unité :
1, z = ![]() , z2,
, z2, ![]() ,
, ![]() ; solutions de l'équation z5 − 1 = 0.
; solutions de l'équation z5 − 1 = 0.
Le polynôme z5 − 1 se factorise sous la forme
z5 − 1 = (z − 1)(z4 + z3 + z2 + z + 1)
(formule classique utilisée pour la somme des
5 premiers termes d'une suite géométrique).
La factorisation peut se poursuivre par
z5 − 1 = (z − 1) (z2 − 2αz + 1) (z2 − 2βz + 1)
avec, par identification, les réels α et β vérifiant :
α + β = − ![]() et αβ = −
et αβ = − ![]() .
.
Dans le triangle IJQ rectangle en Q,
P est le milieu de [IJ] donc OI − OJ = −2 OP = − ![]() ;
;
la relation métrique pour la hauteur [OQ] permet d'écrire :
OI × OJ = OQ2 = ![]() .
α et β sont donc les affixes des points I et J.
.
α et β sont donc les affixes des points I et J.
Il est possible de résoudre le système d'équations α + β = −![]() et α β = −
et α β = − ![]()
et les réels α et β sont les solutions d'une équation du second degré,
mais utilisons
plutôt la calculatrice TI-92 qui permet de factoriser dans C
et en regroupant les facteurs trouvés avec factorC(z^5− 1, z) on a :
(z2 − 2αz + 1)
= 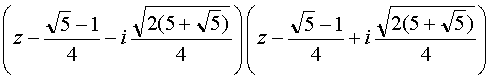
et (z2 − 2βz + 1)
= 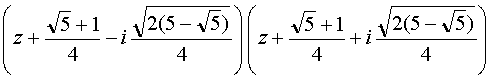
soit z5 − 1 = (z − 1)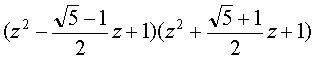 .
.
Dans tous les cas (en vérifiant éventuellement les valeurs des cosinus),
on trouve :α = ![]() = Re(
= Re(![]() ) ;
) ;
partie réelle des solutions de z2 − 2αz + 1 = 0,
et β = − ![]() = Re(
= Re(![]() ) ; partie réelle des solutions de z2 − 2βz + 1 = 0.
) ; partie réelle des solutions de z2 − 2βz + 1 = 0.
α et β sont les parties réelles des racines cinquièmes de l'unité, racines imaginaires.
Les sommets du pentagone régulier sont bien l'intersection
du cercle unité avec les parallèles à (Oy) passant par I et J.
Voir : plan complexe
5. Dessiner un cerf-volant ABVE
Autre variante de la construction de Ptolémée
Méthode
Construction du pentagone à partir du centre O
du cercle circonscrit et d'un sommet A.
Le cercle de « Ptolémée » de centre K passant par A coupe
le diamètre [A’A] en U. Le cercle de centre A’ passant par U
permet de trouver les sommets B et E et
le point V de concours des côtés (BC) et (DE).
Les deux derniers sommets C et D sont les points de
rencontre de ces deux droites avec le cercle circonscrit.
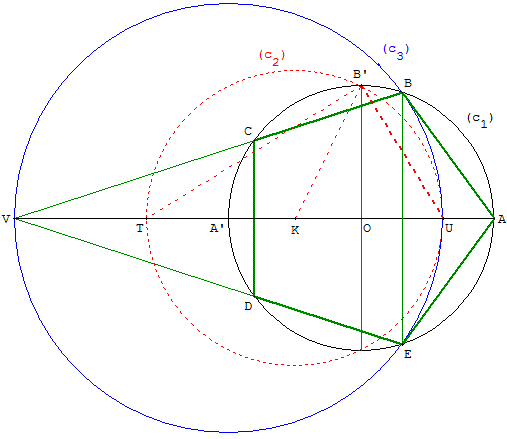
Dessiner le pentagone régulier dans un cercle
Placer deux points O et A et le cercle (c1) de centre O,
passant par A, de rayon r = 1.
A’ est le symétrique de A par rapport à O.
Le point B’ est un des points d'intersection du
diamètre perpendiculaire à [A’A] avec le cercle (c1).
K est le milieu du rayon [A’O].
Le cercle (c2) de « Ptolémée » de centre K
par B’ coupe [OA] en U et [OA’) en T.
Le cercle (c3) de centre A’ passant par U coupe
le cercle (c1) en B et E et la droite (AO) en V.
Les droites (BV) et (EV) coupent le cercle (c1) en C et D.
Les points ABCDE sont les sommets du pentagone cherché.
Démonstration
Comme pour la méthode du R.P. Durand, on a B’U = AB,
côté du polygone convexe, et B’T = BE, côté du pentagone croisé.
On a aussi : A’U = φ = ![]() ainsi que A’B et A’E rayons du cercle (c3).
ainsi que A’B et A’E rayons du cercle (c3).
Dans le cercle (c1) le triangle A’BA,
inscrit dans un demi-cercle, est rectangle en B.
cos AA’B = A’B/A’A = ![]() =
= ![]() = cos
= cos ![]() .
.
Les angles aigus du triangle sont donc ![]() et
et ![]() .
.
L'angle BÂE est égal à ![]() .
.
Les deux segments égaux [AB] et [AE], de longueur égale,
sont deux côtés d'un pentagone régulier inscrit dans le
cercle (c1).
Le triangle isocèle A’BU a un angle au sommet égal à ![]() ,
,
c'est un triangle d'or de côtés A’B = A’U = φ et BU = 1.
Dans le cercle (c3) l'angle inscrit ![]() correspond
correspond
à l'angle au centre EÂ’B = 2 AÂ’B = ![]() .
Cet angle inscrit est donc
.
Cet angle inscrit est donc ![]() =
= ![]() .
.
Les angles aigus du triangle VBA sont égaux à ![]() et
et ![]() .
.
Le troisième angle est ![]() =
= ![]() .
.
Le point C est aussi un sommet du pentagone.
Même démonstration pour D, ce qui permet
de conclure que ABCDE est un pentagone régulier.
6. Méthode des cercles tangents
Construction proposée par Dumont (1996)
à
propos des tracés régulateurs des temples d'Angkor.
Méthode
Tracer le pentagone à partir du centre O
du cercle circonscrit (c1) et d'un sommet A.
Dessiner le cercle (c2) ayant comme diamètre [OR],
un rayon du cercle circonscrit (c1),
perpendiculaire au diamètre [AA’] de (c1).
Deux cercles de centre A’, tangents au cercle (c2),
rencontrent le cercle circonscrit en quatre des
sommets du pentagone
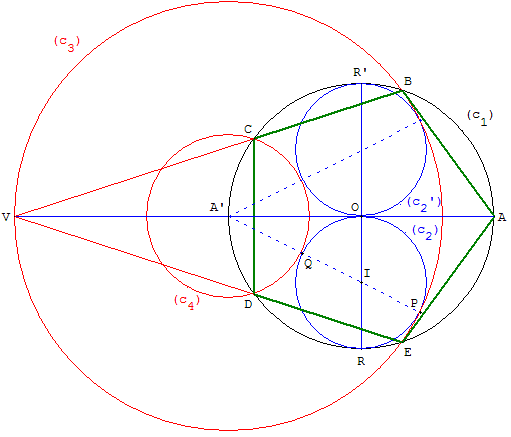
Construction du pentagone régulier au compas
Placer deux points O, A et le cercle (c1) de centre O, de rayon r =1,
passant par A. A’ est le symétrique de A par rapport à O. I est le
milieu d'un rayon perpendiculaire au diamètre [AA’].
(c2) est le cercle de centre I, passant par O.
La droite (A’I) coupe le cercle (c2) en P et Q. (c3) et (c4)
sont les cercles de centre A’ tangents à (c2).
Le cercle (c3) est tangent intérieurement au cercle (c2) en P
et le cercle (c4) est tangent extérieurement au cercle (c2) en Q.
Le cercle (c3) coupe (c1) en B et E et le cercle (c4) coupe (c1) en C et D.
Les points ABCDE sont les sommets du pentagone cherché.
TS : Démonstration par calcul d'affixes de complexes.
En choisissant r = 1 et O comme origine, on va montrer
que l'affixe ω = eiθ de B a pour argument θ = ![]() en calculant cos θ.
en calculant cos θ.
Le rayon de (c3) est A’B tel que ![]() =
= ![]() +
+ ![]() donc A’B = |1 + ω|,
donc A’B = |1 + ω|,
or A’B = A’P = A’I + IP = ![]() +
+ ![]() d'où |1 + ω| =
d'où |1 + ω| = ![]() (le nombre d'or φ).
(le nombre d'or φ).
On a donc |1 + ω|2 = (1 + cos θ)2 + sin2θ = 2(1 + cos θ) = ![]() ,
,
d'où l'on tire cos θ = ![]() soit θ =
soit θ = ![]() (voir angle trigonométrie).
(voir angle trigonométrie).
Démonstration de la méthode des cercles tangents
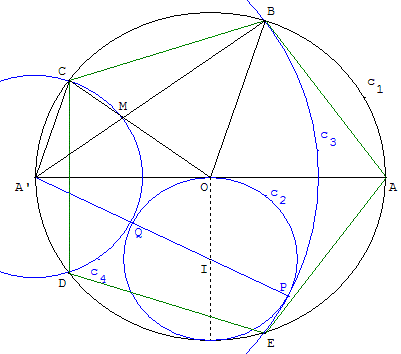
Dans le triangle rectangle A’OI on a :
A’O2 = A’I2 − IO2 = A’I2 − ![]() (puissance du point A’ par rapport au cercle c2)
(puissance du point A’ par rapport au cercle c2)
A’O2 = (A’I − ![]() )(A’I +
)(A’I + ![]() )
)
A’O2 = (A’I − IQ)(A’I + IP) = A’Q . A’P.
A’O2 est donc le produit des rayons des cercles (c3) et (c4).
Soit M le point d'intersection du segment [A’B] et du cercle (c4).
Le produit des rayons est donc :
A’O2 = A’M . A’B, soit ![]() .
.
Ayant déjà l'angle OA’B en commun les
triangles A’MO et A’OB sont semblables.
Le triangle A’OB ayant deux côtés égaux
à r est isocèle, le triangle A’MO l'est aussi.
Soit α la mesure des angles égaux OA’B = ![]() = MOA’.
= MOA’.
Les angles « au sommet » des triangles isocèles
sont donc ![]() = A’OB = π − 2α.
= A’OB = π − 2α.
D'autre part, le triangle BOM est isocèle (puisque BM = r).
D'où MOB = ![]() .
.
On a donc A’OB = π − 2α = A’OM + MOB= α + ![]() .
.
De là, α = ![]() ,
MOB =
,
MOB = ![]() , A’OB =
, A’OB = ![]() .
.
Donc, AOB = ![]() et B est le deuxième sommet du pentagone.
et B est le deuxième sommet du pentagone.
Le point C d'intersection de la demi-droite [OM) et
du cercle (c1) est le troisième sommet du pentagone,
car : COB = MOB = ![]() .
.
Montrons que ce sommet C du pentagone est sur le cercle (c4).
L'angle CA’B inscrit dans le cercle (c1) est égal à la moitié
de l'angle au centre : CA’B = ![]() COB =
COB = ![]() .
.
![]() = MOB =
= MOB = ![]() .
.
Le troisième angle du triangle A’MC est ![]() =
= ![]() .
.
Ce triangle ayant deux angles égaux est isocèle. A’M = A’C.
Le point C est bien sur le cercle (c4).
La symétrie par rapport à (AA’) donne les autres sommets E et D.
Méthode égyptienne de construction du pentagone
Œil d'Oudjat
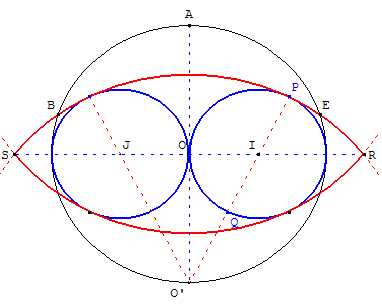
Cette figure est la représentation de l'œil d'Oudjat vue par les Égyptiens.
Les deux arcs de cercle RS forment ce que
les mathématiciens appellent une lentille.
Construction égyptienne du pentagone régulier
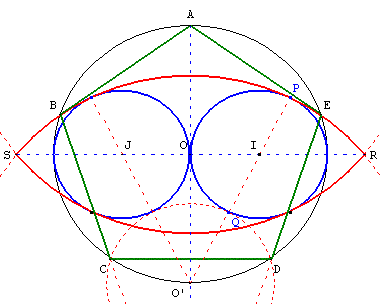
Les points B et E, intersection du cercle de diamètre [AO’]
et d'un des arcs RS, sont deux des sommets du pentagone de côtés [AB] et [AE].
Les sommets C et D complètent le pentagone régulier.
Construction du pentagone à partir d'une diagonale
7. Construction d'Euclide à partir d'une diagonale
Les Éléments d'Euclide - livre IV - Proposition 11
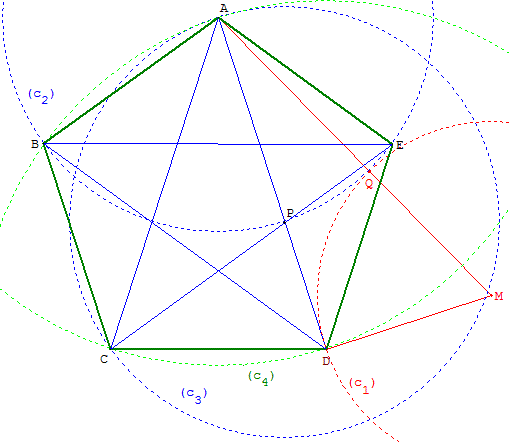
Construction du pentagone avec un triangle d'or
Se donner deux sommets A et D.
La longueur d'un côté partage la diagonale en « moyenne raison ».
Trouver le point P formant une section d'or sur [AD]
avec le triangle ADM, rectangle en D, tel que DM = ![]() AD.
AD.
Construction à partir d'une diagonale [AD]
Tracer le cercle (c1) de centre M passant par D coupant [AM] en Q
et le cercle (c2) de centre A passant par Q.
Le cercle (c2) coupe [AD] en P. Son rayon est égal au
côté du pentagone convexe. Les sommets B et E sont situés sur ce cercle.
Les cercles (c3), de centre P passant par A, et (c4), de centre A
passant par D, se coupent en C sommet du triangle d'or ACD.
Terminer la construction des pentagones :
le point B est à une des intersections du cercle (c2)
et du cercle de centre D passant par A.
Le cercle (c2) recoupe (CP) en E.
ABCDE est un pentagone régulier convexe,
ACEBD est un pentagone régulier étoilé.
8. À partir de la longueur du côté
placée sur une diagonale
Méthode
Se donner deux points A et P tel que AP soit la longueur
du côté. La droite (AP) sera une diagonale du pentagone.
Les points R et D partagent [AP] en « moyenne et extrême raison ».
Trouver le point R formant une section d'or sur [AP]
avec le triangle APM, rectangle en P, tel que PM = ![]() AP.
AP.
Puis reporter AR en P pour trouver le point D.
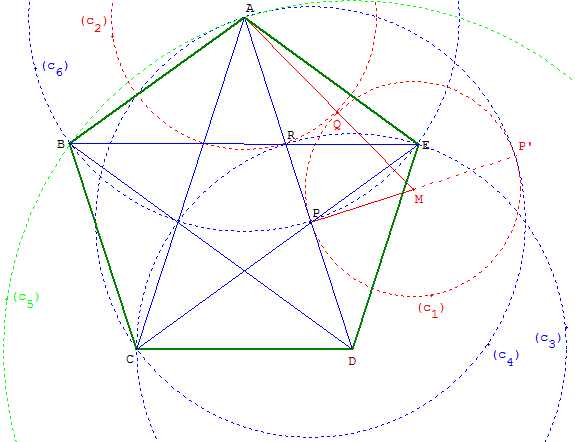
Construction
Tracer le cercle (c1) de centre M passant par P coupant [AM] en Q
et le cercle (c2) de centre A passant par Q.
Le cercle (c2) coupe [AP] en P. et placer D tel que PD = AR.
Les cercles (c3), de centre D passant par R, et (c4),
de centre A passant par A, se coupent en C.
Les cercles (c3), de centre D passant par R, et (c6), de centre A
passant par P, se coupent en E et en un des points d'intersection des diagonales.
Le point B est à une des intersections du cercle (c5) de centre D
passant par A et du cercle (c6) de centre A passant par P.
ABCDE est un pentagone régulier convexe,
ACEBD est un pentagone régulier étoilé.
Construction du pentagone à partir d'un côté
9. Triangle d'or et côtés consécutifs d'un pentagone
Avec la donnée de deux sommets consécutifs, la configuration
ci-dessous est utilisée les trois constructions suivantes.
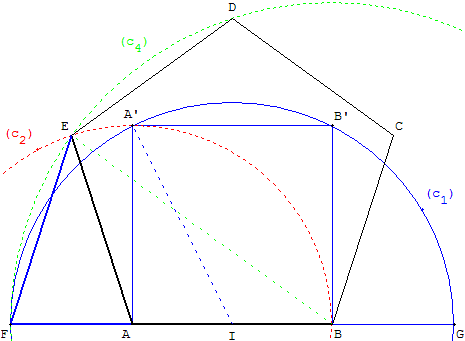
Étant donné un pentagone ABCDE de côté AB = 1,
la diagonale BE mesure φ.
L'angle intérieur BÂE vaut ![]() radians
radians
et le supplémentaire FÂE est ![]() .
.
À partir de deux points A et B il est possible de
trouver la longueur φ d'une diagonale
en réalisant la construction du nombre d'or.
Construction du sommet E du pentagone
Construire un carré ABB’A’ de côté 1.
Soit I le milieu du côté [AB].
Le cercle (c1) de centre I, passant par A’ (et B’),
de rayon ![]() , coupe (AB) en F et G.
, coupe (AB) en F et G.
On a BF = AG = φ.
Les cercles (c2) de centre A passant par B, de rayon 1,
et (c4) de centre B passant par F, de rayon φ, se coupent en E.
Triangles d'or
FA = FB − AB = φ − 1 = ![]() ; AE = 1 ; FÂE =
; AE = 1 ; FÂE = ![]() :
:
AEF est un triangle d'or. EF est donc égal à 1.
FB = EB = φ : EF = 1 : FBE est un triangle d'or
c'est le « triangle intéressant » de Daniel Reisz.
Voir aussi : carré inscrit dans un demi-cercle
10. À partir d'un carré inscrit dans un demi-cercle
Méthode
Construction à partir de deux sommets consécutifs A et B.
Comme expliqué ci-dessus, construire le carré ABB’A’,
de côté a, et le cercle (c1) de centre I, milieu de [AB], passant par A’, de rayon a![]() .
.
Ce cercle coupe (AB) en F et G tels que BF = AB = aφ,
longueur de la diagonale du pentagone.
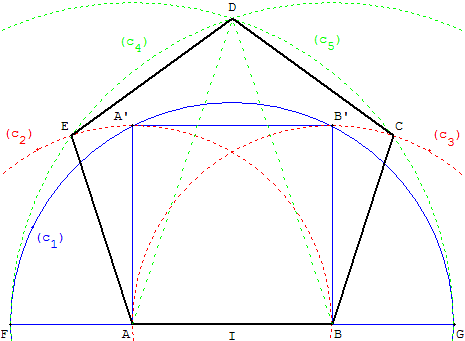
Construction
Les cercles (c2) de centre A passant par B,
de rayon a, et (c4) de centre B passant par F,
de rayon aφ, longueur de la diagonale du pentagone, se coupent en E.
De façon symétrique, les cercles (c3) de centre B passant
par A et (c5) de centre A passant par G se coupent en C.
Les cercles (c4) et (c5), de rayons aφ, se coupent en D,
sur la médiatrice de [AB].
ADB est un triangle d'or de côtés aφ et a.
Pentagones d'Hippocrate
À partir de la figure précédente, création d'un second
pentagone A’B’C’DE’ dont les sommets sont des points remarquables :
• A’ situé sur la diagonale (AD) à l'intersection des cercles (c2) et (c4),
• E’ situé sur le cercle (c2) à l'intersection du côté (AE) et de la droite (A’F).
Les points A et B sont situés aux intersections
de diagonales du pentagone A’B’C’DE’.
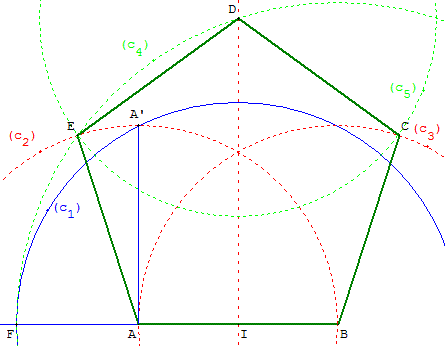
11. Construction d'architecte
Méthode
Dessin du pentagone à partir d'un côté :
les points de base sont deux sommets consécutifs A et B.
Simplification de la construction précédente en
utilisant une seule perpendiculaire (AA’) et non un carré.
Construction
Tracer le cercle (c2) de centre A passant par B.
Soit A’ un des points d'intersection entre ce cercle (c2)
et la droite perpendiculaire à (AB) passant par A.
Soit I le milieu de [AB]. Le cercle (c1) de centre I,
passant par A’, coupe la demi-droite [BA) en F.
Le cercle (c4) de centre B passant par F coupe le cercle (c2) en E.
Il coupe aussi la médiatrice de [AB] en D.
Tracer le cercle (c5) de centre D passant par E,
puis (c3) de centre B passant par A.
Seul un des points d'intersection de ces deux cercles
permet d'obtenir un polygone convexe : le point C.
ABCDE est un pentagone régulier.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
construction d'architecte du pentagone
12. Un triangle intéressant
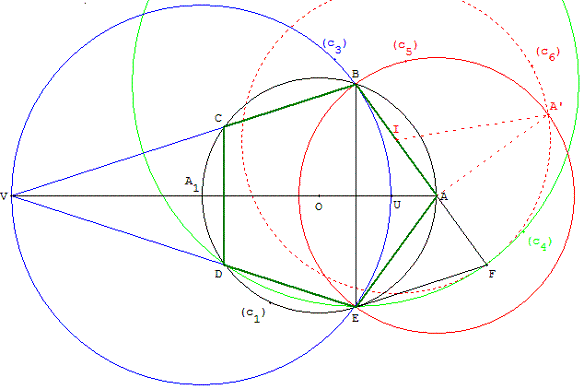
Tracer le triangle d'or BEF. Pour cela, trouver le point F,
avec le triangle rectangle isocèle BAA’ et le cercle (c6) de centre I milieu de [AB].
Le point E est à une des intersections des cercles (c4)
de centre B passant par F et (c5) de centre A passant par B.
Daniel Reisz réalise alors la construction suivante :
Le cercle (c1) est circonscrit au triangle ABE et recoupe (c4) en D.
La perpendiculaire à (BE) passant par A coupe (ED) en V.
La droite (BV) recoupe le cercle circonscrit (c1) en C.
On reconnaît le dessin du cerf-volant (géométrie) ci-dessus.
13. Autre construction du pentagone à partir d'un côté
Comment tracer un pentagone régulier de côté 1.
Dessin à partir du côté [AB] du pentagone :
les points de base sont deux sommets consécutifs A et B tels que AB = 1.
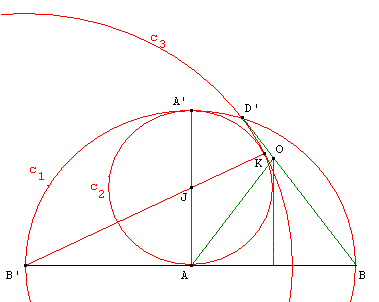
Placer les deux premiers points A et B du polygone,
placer le point B’ symétrique de B par rapport à A,
tracer le cercle (c1) de centre A passant par B (diamètre [B’B]),
construire la perpendiculaire en A à (AB), qui coupe le cercle (c1) en A’.
Soit (c2) le cercle de diamètre [AA’] : son centre J est le milieu de [AA’].
Tracer la droite (B’J), cette droite coupe le cercle (c2) au point K.
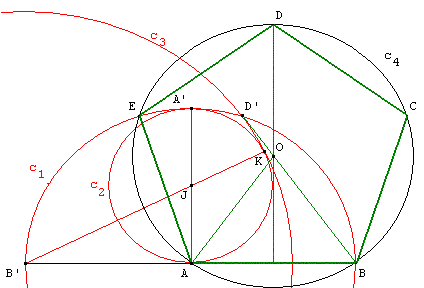
Tracer le cercle (c3) de centre B’ passant par le point K,
les cercles (c1) et (c3) se coupent en D’, tracer le segment [BD’].
La médiatrice de [AB] coupe le segment [BD’] en O :
O est le centre du cercle circonscrit (c4) au pentagone
et on peut vérifier que l'angle AOB mesure 72°.
Pour tracer le pentagone régulier ABCDE,
il suffit de placer le point C symétrique de A par rapport à (OB),
un point E intersection des cercles (c1) et (c4),
le point D est un des points d'intersection du cercle
circonscrit (c4) et de la médiatrice de [AB] qui passe par O.
Table des matières
Dans d'autres pages du site
Pentagone - Constructions approchées
Construction des bâtisseurs du Moyen-âge
Construction dite « de Thalès »
Propriétés du pentagone
Centre de gravité
Origami du pentagone
Construction exacte par pliage d'un nœud
Constructions du pentagone avec quatre règles à bords parallèles
Problèmes de construction en 1ère L
Suites et TI-92
Pentagone, nombre d'or et suite de Fibonacci
![]() Feuille de travail dynamique avec GeoGebra : pentagone
Feuille de travail dynamique avec GeoGebra : pentagone
PENTAGONE RÉGULIER – Constructions
![]() Google friendly ; sur ordinateur : cette page pour grand écran
Google friendly ; sur ordinateur : cette page pour grand écran
La première page de ce document n'est pas une image,
et une copie ne devrait pas être référencée comme telle par Google !
Copyright 2003 - © Patrice Debart
|
Page no 39, réalisée le 22/4/2003 |