Descartes et les Mathématiques
Fractions égyptiennes
Décomposition d'un nombre rationnel en fractions égyptiennes, conjecture de Sierpinski.
Sommaire
1. Légende : l'œil Oudjat
2. Décomposition d'un nombre positif en fractions égyptiennes
Fraction de numérateur 4 - Conjecture d'Erdös
4. Conjecture de Sierpinski
Fraction de numérateur 5
Stage « Mathématiques et informatique »
Ouagadougou - février 1999
Une fraction égyptienne est une somme d'inverses de naturels, avec ces naturels tous différents.
Les anciens Égyptiens réduisaient donc les fractions à des sommes de fractions unitaires de numérateur 1, avec 
comme exception..
Ils préfèrent les décompositions qui utilisent les dénominateurs les plus petits.
Une décomposition avec deux termes est préférée à celles à trois termes. Il n'y a pas plus de trois fractions unitaires.
Les dénominateurs sont classés par ordre croissant. On ne répète jamais un dénominateur.
La représentation sous forme d'une somme de fractions à numérateurs unitaires n'est pas unique.
Ils minimisaient le premier dénominateur, mais acceptaient un premier dénominateur plus
grand si cela réduisait le dernier.
Cette décomposition complexe était encore utilisée par Fibonacci.
La décomposition d'un rationnel positif, inférieur à 1, en fraction égyptienne permet de mettre en œuvre des exercices de la quatrième à la terminale S avec des méthodes empiriques et des exemples simples d'algorithmes.
1. Légende : l'œil Oudjat
L'œil Oudjat est un hybride d'œil humain et d'œil de faucon : il représente un œil humain fardé et souligné de deux marques colorées caractéristiques du faucon pèlerin.
Il serait œil d'Horus, fils d'Isis et d'Osiris, perdu dans un combat mené contre son oncle Seth pour venger son père.
Le dieu Thot, guérisseur et dieu de la médecine, l'avait soigné et le lui avait rendu. C'est pourquoi « Oudjat » symbolisait la santé et la lumière. L'Oudjat incarnait aussi le cycle du jour et de la nuit.
On le retrouve comme amulette sur les momies : l'amulette représentait aussi l'attachement du fils à son père, car Horus avait donné son œil à son père Osiris afin qu'il recouvre la vue.
Les « anciens Égyptiens » avaient coutume d'encastrer l'Oudjat dans les niches de leurs portes pour se préserver du mauvais œil.
Au début du XXe siècle, fut inventée la légende de l'identification de l'œil Oudjat avec des fractions, légende qui sera répétée jusqu'à la fin du siècle :
les parties constituantes de l'œil Oudjat serviraient à écrire les différentes fractions ayant 64 comme dénominateur, ce qui permettait de compter le grain, dont l'unité de mesure était le hékat (un hékat valait environ 4,785 litres).
L'œil d'Horus serait décomposé en six éléments de la façon suivante :
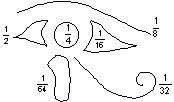
– la petite pyramide = 
– le soleil = 
– la grande pyramide = 
– la ligne de sol = 
– le bloc poussé par l'Égyptien = 
– la ligne recourbée = 
Au cours du combat, Seth arrache l'œil gauche d'Horus, le coupe en six morceaux et le jette dans le Nil. À l'aide d'un filet, Thot récupère les morceaux, mais il en manque un !
La somme des fractions de l'Oudjat ne fait que 
;
le manquant est le liant magique qui sera ajouté par le dieu Thot pour rendre à Horus son intégrité vitale, en permettant à l'œil de fonctionner.
Ce , manquant pour parfaire l'unité, serait toujours fourni par Thot, patron des scribes, au calculateur, qui se placerait ainsi sous sa protection.
2. Décomposition d'un rationnel en fraction égyptienne
2.a. Introduction
Dès l'an 2000 avant notre ère, l'Égypte antique connaissait les fractions sous une forme limitée aux inverses d'entiers.
Exemples
Un algorithme
Henry Plane, Plot n° 60
Pour une fraction 0 < 
< 1, recherchons deux naturels n et r tels que np = q + r
et nous divisons cette égalité par nq :
(np)/(nq) = q/(nq) + r/(nq)
et donc = 1/n + r/(nq)
= 
= +
= + 2/(2 × 4) = + 
= 
= + 
+ 
.
7n = 11 + r soit n = 2, r = 3 et = + 3/22
et on recommence avec 3/22, on che rche 3n = 22 + r soit n = 8, r = 2
et 3/22 = 
+ 2/(8 × 22) = + 1/88
On a donc une autre décomposition = + + 1/88
= 
= +
= +16/(4 × 20) = +
Par exemple 
= 
= + ,
mais on a aussi = 
+ 
+ car 
(formule du « Matching pair ») ;
= + 2/(2 × 8) = +
Ou encore 
= 
= + 
ou = + = + + 
.
Il est ainsi possible d'obtenir une infinité de décompositions.
C'est pourquoi les Égyptiens avaient décidé d'utiliser celle contenant le moins de termes et n'en répétant aucun.
2n = 5 + r soit n = 3, r = 1
= + 1/(3 ×5) = +
2.b. Trois méthodes
Il s'agit de décomposer un rationnel de ]0 ; 1[ en une somme d'inverses d'entiers strictement croissants.
Il peut être montré que tout nombre rationnels positif, inférieur à 1, peut être écrit sous cette forme et ce, d'une infinité de façons différentes.
On ne sait pas très bien comment les Égyptiens procédaient pour obtenir ces décompositions.
Deux méthodes égyptiennes
Méthode de Taton (2000 avant J.-C.)
Dénominateur pair.
Décomposer le numérateur en somme de puissances de 2 :
= 
= 
+ 
+ 
= + + ,
En ajoutant les deux premières fractions
= ( + ) + = (2/6 + ) + = +
Mais aussi en ajoutant les deux dernières fractions
= + ( + ) = + (2/12 + ) = +
7n = 12 + r soit n = 2, r = 2
= + 2/(2 × 12) = +
7n = 12 + r soit n = 3, r = 9
= + 9/(3 × 12) = +
Numérateur égal à 2
« table de deux » du Papyrus Rhind
Les « anciens Égyptiens » devaient avoir différentes tables permettant de décomposer les fractions.
La table dite « de deux », se trouve dans le papyrus de Rhind. Elle répertorie les fractions dont le numérateur est 2 et dont le dénominateur varie de 3 à 101.
= 4/18 = (3 + 1)/18 = + 
2n = 9 + r soit n = 5, r = 1 et = + 1/(5 × 9) = + 1/45
ou bien 2n = 9 + r soit n = 6, r = 3
et = + 3/(6 × 9) = +
Une fraction irréductible de numérateur 2 peut s'écrire sous la forme 
.
Comme = 
+ 
, la fraction se décompose en exactement deux fractions égyptiennes.
Exemple : 
= 
= + 
.
Si le dénominateur n'est pas premier, on trouve une autre décomposition la fraction du type 
(p et q impairs) avec la formule :
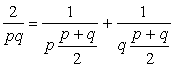
Par exemple, avec p = 3 et q = 5, on a aussi : = + 
.
Autre exemple : pour p = 4, on a 
= 
= + 
.
2/5 = 6/15 = (5 + 1)/15 = + 1/15
2/7 = 8/28 = (7 + 1)/28 = + 1/28
2/11 = 12/66 = (11 + 1)/66 = + 1/66
d'où 2/(5k) = 1/(3k) + 1/(15k)
2/(7k) = 1/(4k) + 1/(28k)
2/(11k) = 1/(6k) + 1/(66k)
Méthode « Matching pair »
(méthode récente du 20e siècle)
Remplacer les doubles d'inverses avec la formule .
|
|
comme |
d'où |
= 
;
+ 
, on a 
= 
+ 
,Un cas particulier pour = + qui n'est pas un développement acceptable et les anciens Égyptiens considéraient cette fraction comme une exception..
Transformer alors un des termes en double par « Matching pair » avec la formule .
Soit pour le deuxième tiers = + 
,
et l'on obtient = + + ,
mais = 
= +
D'où 2/(3k) = 1/(2k) + 1/(6k)
ou avec l'algorithme 2.a. on a 2n = 3+ r soit n = 2, r = 1
donc = + 1/(2 × 3) = +
La méthode « Matching pair » s'utilise de même lorsque, dans des développements, on trouve des fractions unitaires égales.
2.c. Quelques exemples à réaliser en classe
Travail de groupes sur les mêmes fractions.
Un rapporteur écrit au tableau les résultats de son groupe.
Comparaison des résultats (unicité, « meilleure décomposition possible »…).
Fraction de numérateur 3
Soit une fraction irréductible de type 
.
Si le dénominateur n est pair, on a la décomposition 
= 
+ 
.
Sinon n est de la forme 6k – 1 ou 6k + 1.
Si n est de la forme 6k – 1 alors 
= + 
:
|
|
|
 = +  .
|
= 
= 
;Si n est de la forme 6k + 1, utiliser par exemple l'algorithme de Fibonacci ci-dessous.
Recherche empirique plus compliquée
= + + 
.
Cela devient difficile (impossible ?) à la main pour 
= + + + 1/171. D'où la nécessité d'un algorithme.
Pour un numérateur égal à 4 ou 5, voir les conjectures d'Erdös ou de Sierpinski ci-dessous.
2.d. Algorithme de Fibonacci
Expression clé : algorithme fraction égyptienne
Recherche et programmation d'un algorithme
Première phase de recherche par groupes.
On espère voir sortir l'encadrement de la fraction par deux inverses d'entiers consécutifs n et n+1.
Sinon, on le suggère.
Deuxième phase de recherche au terme de laquelle l'algorithme sera soit trouvé soit donné.
Algorithme glouton de Fibonacci
En 1201, Fibonacci (Léonard de Pise 1175-1250) prouva que tout nombre rationnel, compris entre 0 et 1, pouvait s'écrire sous la forme d'une somme de fractions à numérateur unitaire et proposa la méthode suivante (pour toute fraction distincte de ) :
« Soustraire à la fraction donnée la plus grande fraction égyptienne possible, répéter l'opération avec la nouvelle fraction, et ainsi de suite jusqu'à ce que l'opération donne une fraction égyptienne. »
Cet algorithme permet l'obtention des dénominateurs n de la décomposition de :
Il suffit, si p > 1, de calculer la partie entière n de 
+ 1,
puis de calculer - 
,
et de recommencer, avec cette dernière fraction, jusqu'à ce que le numérateur soit égal à 1.
Voir programme TI-92
Exemple : on retrouve la décomposition de la fraction , ci-dessus.
Pour = avec p = 2 ; q = 15,
+ 1 = 
+ 1 = 
, d'où n = partie entière(8,5) = 8,
- = - = ,
d'où = + .
Remarque : cet algorithme est peu performant, car on tombe facilement sur de grands nombres.
Le tester sur des types de matériels informatiques différents (calculatrices, ordinateurs…).
Comparer les difficultés rencontrées, les performances et les résultats.
Explications guidées pas à pas, sous forme d'exercice de recherche en classe, puis rédaction à la maison :
- Recherche du dénominateur n de la fraction .
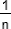- Exprimer
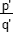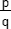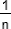= - (sous forme de fraction irréductible). - La suite des numérateurs p’ des différences est strictement décroissante, ce qui assure la finitude du processus.
- Dans la décomposition, la suite des dénominateurs n est strictement croissante (toutes les fractions sont distinctes).
On obtient : 
= + 
+ 
; mais on a aussi = + 
+ 
.
On peut ainsi trouver : 
= + + 
; mais = + + 
;
ou encore 
= + + ; mais = + + ;
Développement unique de longueur 3 : 
= + + .
2.f. Prolongements et limites de l'algorithme
(travail maison)
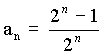: en utilisant la somme des termes d'une suite géométrique, trouver une décomposition de an en fractions égyptiennes et comparer cette décomposition avec celle de l'algorithme de Fibonacci.
On a : a2 =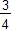 = 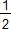+ ; a3 =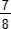 
= 
= + + = + + 
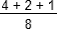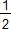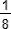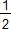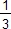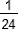.; a4 = 
= + + + = + + 
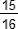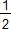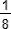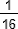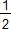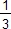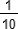+ 1/240.
a6 = 63/64 =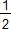 + + + + 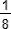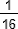1/32 + 1/64 (CRPE 2012)- Une limite de l'algorithme : calculer une décomposition en fractions égyptiennes de
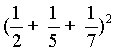par deux méthodes différentes.
On trouve aussi 3481/4900 =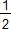 + + 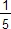1/97 + 1/10113 + 1/… = 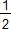+ + 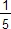1/98 + 1/4900 = 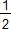+ + 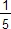1/100 + 1/2450. - Une autre limite : sur certains matériels, les grands dénominateurs que donne l'algorithme dépassent les capacités de calcul (exemple sur Excel).
2.g. Conjecture d'Erdös--Straus
Fraction de numérateur 4
Une fraction irréductible 
a un dénominateur n de la forme 4k – 1 ou 4k + 1.
Pour un dénominateur 4k – 1, on a une décomposition en deux fractions unitaires : 
= + 
.
Dans le cas général, la conjecture d'Erdös énonce que toute fraction irréductible de numérateur 4 a une décomposition de longueur 3 :
Pour tout entier n > 1 il existe trois naturels a, b et c tels que
4 |
1 |
1 |
1 |
|||
= |
+ |
+ |
||||
n |
a |
b |
c |
Remarque : contrairement aux fractions égyptiennes on n'impose pas à a, b et c d'être tous différents.
Le nombre maximum de fractions obtenues par l'algorithme de Fibonacci dans la décomposition de ,
avec n > 4, est quatre :
la suite des numérateurs p’ étant dans la liste {4, 3, 2, 1}.
Par exemple
4/7 = 8/14 =(7+1)/14 = + 1/14.
= + + = + 
+
Étudier
= + 
+ 
+ 
mais = + = + +
( fraction de numérateur 3 calculée ci-dessus)
De même décomposer 
avec l'algorithme… et pourtant :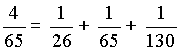
.
Allan Swett a confirmé que la décomposition en trois fractions unitaires admet des solutions pour n jusqu'à 1014, mais la conjecture n'a pas été démontrée.
3. Waclaw Sierpinski (Varsovie 1882 - 1969)
Mathématicien polonais, professeur à l'université de Lvov puis de Varsovie, il consacre ses recherches à la théorie des nombres.
Il est bien connu par ses travaux :
- sur la théorie analytique des nombres,
- sur les images fractales : à partir d'une figure de base, répéter indéfiniment une transformation,
- sur les courbes permettant de remplir un carré.
Fractales de Sierpinski
Le triangle de Sierpinski est obtenu en partant d'un grand triangle équilatéral. On prend les milieux de chacun de ses côtés et on enlève le triangle équilatéral ainsi obtenu. On obtient alors trois nouveaux petits triangles équilatéraux. On recommence alors l'opération précédente, à chacun de ces nouveaux triangles, et ainsi de suite. On obtient alors neuf, vingt-sept, quatre-vingt-un… nouveaux triangles.
Le tapis de Sierpinski est obtenu de même en découpant un grand carré en 9 petits carrés et on enlève le carré central. On applique à nouveau le même procédé à chacun des 8 petits carrés restants… et ainsi de suite.
Enfin, l'hexagone de Sierpinski est obtenu de même en découpant un grand hexagone en 7 petits hexagones (partager chaque côté en trois parties égales et de part et d'autre de chaque sommet tracer les segments parallèles à la diagonale issue de ce sommet). On enlève l'hexagone central. On applique à nouveau le même procédé à chacun des 6 petits hexagones restants… et ainsi de suite.
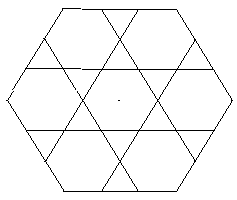D'après Olivier Orochoir
Cécile Kerboul – Plot no 104 – mars 2003
Télécharger la figure GéoPlan hex_sier.g2w
4. Conjecture de Sierpinski
Une conjecture de Sierpinski énonce que toute fraction irréductible de numérateur 5 a une décomposition de longueur 3.
Pour tout entier n > 1 il existe trois naturels a, b et c tels que
5 |
1 |
1 |
1 |
|||
= |
+ |
+ |
||||
n |
a |
b |
c |
Remarque : contrairement aux fractions égyptiennes on n'impose pas à a, b et c d'être tous différents.
4.a. Quelques pistes de recherche
Si le dénominateur n est multiple de 2 : n = 2p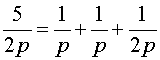 
si n est multiple de 3 : n = 3p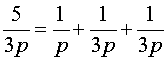 
Pour les nombres n premiers de 7 à 37, en s'aidant éventuellement de l'algorithme de la deuxième partie, on a les résultats suivants :
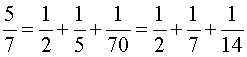
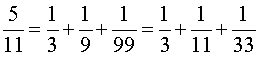
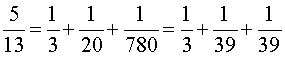
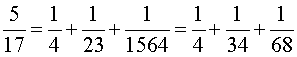
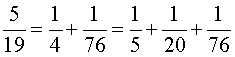
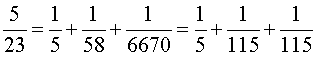
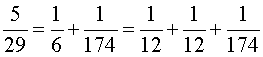
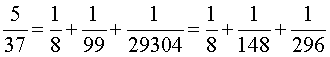
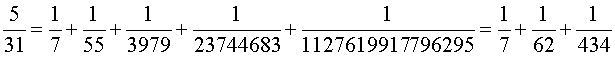
On remarque :
– qu'en général, la décomposition n'est pas unique,
– que, si l'algorithme de Fibonacci permet d'obtenir trois fractions, le dernier nombre c est, en général, assez grand.
4.b. Algorithme
Pour n fixé, choisir a égal à la partie entière de 
.
Calculer de 1 en 1 les valeurs de b jusqu'à trouver que
le nombre 
soit l'inverse d'un entier.
En cas d'échec recommencer en augmentant a de 1.
Le plus efficace est de calculer de -1 en -1 pour b à partir de la partie entière de 
jusqu'à a.
Table des matières
Dans d'autres pages du site
Index algorithme et calculatrice
TI-92 : petits programmes
π et le papyrus Rhind : grands problèmes
Google friendly
Copie Twitter : t.co/ilsVkCfLQc
Copyright 2002 - © Patrice Debart
Téléchargement
Télécharger fracegypt.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image
et une copie ne devrait pas être référencée comme telle par Google !
Malgré tout, Google considère l'URL originale comme une erreur de type "soft 404".
Liens - Rétroliens
Calculateur de fractions : Egyptian fractions
Gilles Dubois Mathématiques - (licence-cpge)
Page no 28, créée le 16/12/2002
mise à jour le 26/7/2018