 Descartes et les Mathématiques
Descartes et les Mathématiques
Fibonacci (1170-1250)
Un grand mathématicien du moyen-âge
Léonard de Pise dit Fibonacci
Son œuvre fondamentale fut l'introduction des chiffres indo-arabes,
du zéro et la notation positionnelle du système décimal.
Fibonacci utilisait le symbole racine carrée √ pour les radicaux.
Une histoire couple de lapins qui donnent naissance
à un couple d'animaux qui à la génération suivante
donne naissance à un nouveau couple et ainsi de suite…
d'où les nombres et la suite de Fibonacci.
« Liber Abaci ».
Sommaire
1. Hauteur d"une tour
2. Les oiseaux
2.1. Solution
1. La géométrie dans le Liber Abaci
Au sommet d'une tour se trouve une hampe d'une hauteur de 20 pieds.
La hampe se brise et tombe au sol sans se détacher de la tour
de telle manière que son extrémité touche le sol
à une distance de 12 pieds de la base de la tour.
Quelle est la hauteur de la tour ?
Un simple application du théorème de Pythagore
donne 16 pieds comme solution.
2. Les oiseaux

Entre deux tours,
l'une de 30 m de haut,
l’autre de 40 m. de haut,
distantes de 50 m,
et en ligne droite
avec les deux bases,
se trouve une fontaine.
Des sommets des tours,
deux oiseaux s’envolent
en même temps à la même
vitesse en direction de la
fontaine et y arrivent
en même temps.
A quelle distance
la fontaine est-elle
de la plus haute tour ?
2.1. Solution
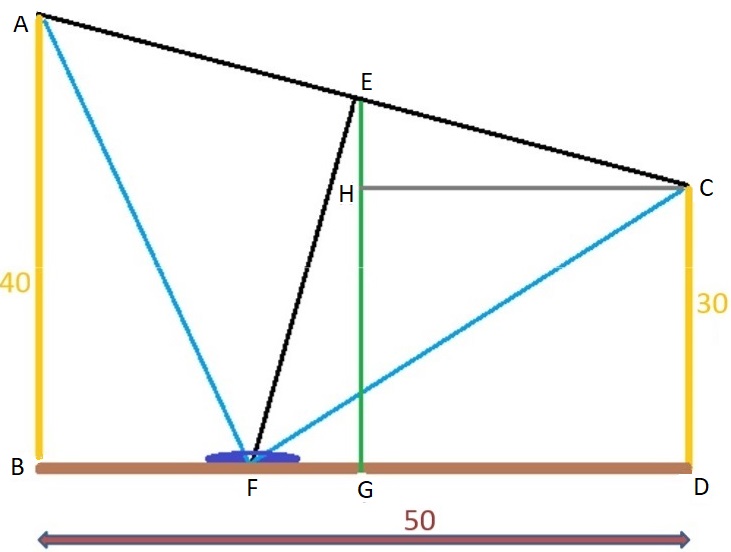
Conformément à la figure ci-dessus,
E et G sont les milieux de [AC] et [BD] et F la fontaine.
EG = (AB + CD)/2 = 35 et EH = EG - GH = 35 - 30 = 5
et CH = DG = DB/2 = 50/2 = 25.
Comme les oiseaux parcourent la même distance,
le triangle ACF est isocèle
et [EF] est la médiatrice de [AC].
Les triangles rectangles EFG et CEH ont leurs côtés
perpendiculaires deux à deux.
Les angles sont égaux et iles triangles sont semblables.
La proportion entre leurs côtés correspondants :
FG/EH = EG/CH
d'où FG/5 = 35/25, soit FG = 7.
BF = 25 - 7 = 18 et FD = 25 +7 = 32.
La fontaine est à 18 m. de la plus haute tour et à 32 m. de la plus petite.
De manière algébrique, avec la propriété de Pythagore
dans les triangles rectangles ABF et CDF de mêmes hypoténuses,
on a AF2 = AB2 + BF2 et CF2 = CD2 + DF2,
soit BF2 + AB2 = FD2 + CD2
Avec BF = x, FD = 50 - x, le problème se ramène à la résolution de l'équation :
x2 + 1600 = (50 - x)2 + 900
soit 100 x = 2500 + 900 - 1600 = 1800 et x = 18.
3. Œuvre de Fibonacci
Le Liber abaci est un ouvrage paru en 1202 que
l'on peut traduire en Livre du calcul ou Livre de l'abaque.
C'est un des premiers ouvrages de l 'Europe du moyen-âge
à vulgariser les chiffres indo-arabes.
Les deux exercices ci-dessus sont extraits de Fibonacci,
dans la collection génies mathématiques - RBA.
Problèmes numériques avec Fibonacci : Les deux images
proviennent de l'atelier des journées de l'APMEP de Marseille.
Table des matières
![]() Mobile friendly
Mobile friendly
Dans d'autres pages du site
Index histoire des mathématiques
Nombre d'or, nombres et suite de Fibonacci
Fractions égyptiennes : algorithme de Fibonacci
La Géométrie de Descartes
Page no 208, créée le 28/7/2018