Descartes et les Mathématiques

La Géométrie de Descartes - Livre premier

Les opérations arithmétiques

Fac-similéde de « La Géométrie » de René Descartes et commentaires sur les opérations algébriques, le théorème de Thalès,
et l'équation du second degré, permettant de retrouver une démarche historique dans l'enseignement des mathématiques.

Table des matières - Livre premier

1. La Géométrie - Introduction

La Géométrie de Descartes est le troisième essai du Discours de la Méthode publié à Leyde en 1637 par René Descartes ; cet ouvrage de mathématiques a eu une répercussion mondiale conduisant notamment à la numérisation de la géométrie.

La Géométrie demeure aujourd'hui, comme au moment de sa parution, un livre de lecture difficile. Malgré tout, des extraits du début du chapitre 3 peuvent être étudiés à partir de la classe de seconde, voire en troisième.

En La Géométrie dit-il, «  je tâche à donner une façon générale pour résoudre tous les problèmes qui ne l'on encore jamais été. »
Il demande qu'on prenne la peine de lire « La Géométrie » la plume à la main en suivant tous les calculs qui peuvent sembler d'abord difficile ; mais on devrait s'y habituer en peu de jours.
Il conseille de passer du premier au « troisième livre, avant de lire le second. »

Descartes impatient expose l'essentiel d'une solution neuve dans l'ordre de l'invention et il répugne à passer du temps pour la démontrer.

La méthode de Descartes est de traiter tout problème de géométrie par le calcul.
Il l'applique ici aux opérations arithmétiques, qui avec le choix d'une longueur pour unité, peuvent être représentée en géométrie par l'emploi de la droite et du cercle.
Donc les racines des équations du second degré peuvent se construire avec la règle et le compas. La construction n'est donnée que pour les racines positives, que Descartes appelle vraies.

Aduertiſſement (page 296)

Iuſques icy i'ay taſché de me rendre intelligible a tout le monde; mais pour ce traité ie crains, qu'il ne pourra eſtre leu que par ceux qui ſçauent deſia ce qui eſt dans les liures de Geometrie : car d'autant qu'ils contienent pluſieurs verités fort bien démonſtrées, i'ay creu qu'il ſeroit ſuperflus de les repeter, & n'ay pas laiſſé, pour cela, de m'en ſeruir.

Cette transcription lettre à lettre de la typographie de Descartes est un passé révolu, source de fautes d'orthographe et inutile, car l'image, comme ici quand elle est nette, se suffit à elle-même.

La ponctuation des éditions de Descartes est assez aléatoire : dans ce document on trouve un point-virgule après monde et deux points après Géométrie, dans la page de Gallica-BNF on trouve une virgule et un point non suivi d'une majuscule. J'ai donc modernisé l'orthographe, les accents et la ponctuation, en donnant le meilleur sens au texte, me fiant dans certains cas ambigus à l'usage du correcteur Antidote.

Comme le mot à mot est illisible et que le but de ces pages est de « rendre Descartes intelligible à tout le monde », j'ai adopté le point de vue Victor Cousin, de traduction en français modernisé comme suit :

Avertissement

Jusqu'ici (dans le discours de la méthode et ses annexes, qui précèdent La Géométrie), j'ai tâché de me rendre intelligible à tout le monde, mais pour ce traité, je crains qu'il ne pourra (puisse) être lu que par ceux qui savent déjà ce qui est dans les livres de Géométrie : car, d'autant qu'ils contiennent plusieurs vérités fort bien démontrées, j'ai cru qu'il serait superflu de les répéter, et n'ai pas laissé, pour cela, de m'en servir.

Note de l'éditeur : comme la page de couverture, cet avertissement ne fait partie de l'édition de David Eugene Smith, je les ai ajoutés à La Géométrie, par cohérence avec le discours de la méthode pour justifier la pagination à partir de la page 297.

Dès cette introduction, Descartes paraît ainsi se faire l'adepte des méthodes actives. Tout au long de son traité, il ne cessera de réaffirmer cette position :

« Au reſte i'ay omis icy les demonſtrations de la plus part de ce que iay dit a cauſe qu'elles m'ont ſemblé si faciles, que pourvûque vous preniés la peine d'examiner methodiquement ſi iay failly, elles se presenteront a vous d'elles meſme : & il sera plus vtile de les apprendre en cete façon, qu'en les liſant. » (livre troisième, page 389)

Avec un certain humour, ce parti pris de l'auteur rend l'ouvrage exploitable au lycée.

Ci-dessous, les exemples du début du Livre Premier où sont exposées les constructions géométriques concernant le produit et le quotient de deux nombres, ainsi que la racine carrée d'un nombre, qui peuvent s'obtenir à la règle et au compas..

2. « La Géométrie » - Livre Premier

La Géométrie - Chapitre premier - Page 297

La résolution géométrique selon Descartes

Des problèmes qu'on peut construire sans y employer que des cercles et des lignes droites

C'est-à-dire à la règle et au compas.

ous les Problèmes de Géométrie se peuvent facilement réduire à tels termes, qu'il n'est besoin par après que de connaître la longueur de quelques lignes droites, pour les construire.

Tous les problèmes de géométrie peuvent se réduire à des calculs numériques.

C'est la pensée fondamentale de Descartes qui fonde la géométrie analytique.

Comment le calcul d'Arithmétique se rapporte aux opérations de Géométrie

En géométrie, l'introduction d'un segment unité permet de réaliser toutes les opérations arithmétiques.

Et comme toute l'Arithmétique n'est composée, que de quatre ou cinq opérations, qui sont l'Addition, la Soustraction, la Multiplication, la Division, et l'Extraction des racines, qu'on peut prendre pour une espèce de Division : Ainsi n'a-t-on autre chose à faire en Géométrie touchant les lignes qu'on cherche, pour les préparer à être connues, que leur en ajouter d'autres, ou en ôter, ou bien en ayant une, que je nommerai l'unité pour la rapporter d'autant mieux aux nombres, et qui peut ordinairement être prise à discrétion, puis en ayant encore deux autres, en trouver une quatrième, qui soit à l'une de ces deux, comme l'autre est à l'unité, ce qui est le même que la Multiplication ; ou bien en trouver une quatrième qui soit à l'une de ces deux, comme l'unité

La Géométrie - Chapitre premier - Page 298

est à l'autre, ce qui est le même que la Division ; ou enfin trouver une, ou deux, ou plusieurs moyennes proportionnelles entre l'unité, et quelque autre ligne ; ce qui est le même que tirer la racine carrée, ou cubique, etc. Et je ne craindrai pas d'introduire ces termes d'Arithmétique en la Géométrie, afin de me rendre plus intelligible.

Descartes traduit les opérations par une figure géométrique (triangles de Thalès) mettant en valeur les proportions.
Une de ces grandes innovations sera de prendre une unité.

Avec C = 1, on a les proportions suivantes, pour
  – la multiplication x de a par b : ,
  – la division x de a par b : ,
  – la racine x de a : ,
  – les moyennes proportionnelles x et y pour la racine cubique de a : (voir Livre troisième).

3. Comment se font géométriquement la multiplication, la division et l'extraction de la racine carrée

Titre dans une édition postérieure

Le théorème de Thalès : Descartes commence sa Géométrie en introduisant l'unité dans une configuration de notre théorème de Thalès : la multiplication est construite comme une longueur et non comme une aire, ce qui va lui permettre la numérisation de la géométrie.

La Multiplication

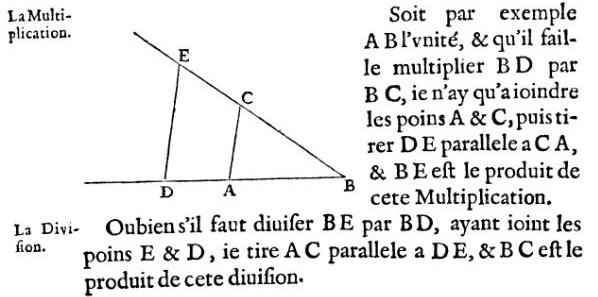
Il suffit de lire sur la figure l'égalité de rapports BE/BD = BC/AB soit a/b = c/1 ; en prenant pour unité AB = 1,
pour en déduire le produit a = b.c.

Soit par exemple AB l'unité, et qu'il faille multiplier BD par BC, je n'ai qu'a joindre les points A et C, puis tirer DE parallèle à CA, et BE est le produit de cette Multiplication.

La Division

De même des rapports BE/BD = BC/AB soit a/b = c/1 ; on peut déduire le quotient c = a/b.

Ou bien s'il faut diviser BE par BD, ayant joint les points E et D, je tire AC parallèle à DE, et BC est le produit de cette division.

La multiplication de 2 par 3

La division de 5 par 3

4. L'Extraction de la racine carrée

La Géométrie - Racine carré - Page 298

Ou s'il faut tirer la racine carrée de GH, je lui ajoute en ligne droite FG, qui est l'unité, et divisant FH en deux parties égales au point K, du centre K je tire le cercle FIH, puis élevant du point G une ligne droite jusqu'à I, à angles droits sur FH, c'est GI la racine cherchée.

Le carré de la hauteur GI issue de l'angle droit du triangle rectangle FIH est égal au produit FG × GH des longueurs des segments découpés sur l'hypoténuse.

GI² = FG × GH = 1 × GH = GH, soit : GI =

Je ne dis rien ici de la racine cubique, ni des autres, à cause que j'en parlerai plus commodément ci-après.

La démonstration de cette propriété se fait dès la classe de troisième en remarquant que le triangle FIH, inscrit dans un demi-cercle, est rectangle en I. Les tangentes des angles H et Î des triangles rectangles semblables IHG et FIG sont égales.

tan H = , tan Î = ; d'où l'égalité des rapports = .

Le produit des « extrêmes » est égal au produit des « moyens » :
GI² = FG × GH = 1 × GH = GH.
GI est la moyenne géométrique de FG et GH : GI = .

Cette construction, due à Euclide, était connue, avant Descartes, par exemple de Bombelli (1526-1572) qui la cite dans son algebra publiée en 1572.

Télécharger la figure GéoPlan cerc_rac.g2w

Bas de la page 298

Comment on peut user de chiffres en géométrie

Mais souvent on n'a pas besoin de tracer ainsi ces lignes

La Géométrie - Chapitre premier - Page 299

sur le papier, et il suffit de les désigner par quelques lettres, chacune par une seule.

Comme pour ajouter la ligne BD à GH, je nomme l'une a et l'autre b, et écris a + b ;
et a – b pour soustraire b de a ; et ab pour les multiplier l'une par l'autre ;

et ab pour les multiplier l'une par l'autre ; et pour diviser a par b ; et aa ou a² pour multiplier a par soi-même (cependant, Descartes répète presque toujours les facteurs égaux lorsqu'ils ne sont qu'au nombre de deux. Ici, comme Victor Cousin, nous avons constamment adopté la notation a².) ; et a³ pour le multiplier encore une fois par a, et ainsi à l'infini ;

et pour tirer

la racine carrée de a² + b² ;
et , pour tirer la racine cubique de a³ – b³ + ab², et ainsi des autres.

Descartes invente ici le signe et l'utilise indifféremment pour la racine carrée ou avec la constante C homogène indique la racine cubique .

Descartes n'utilise pas de parenthèse dans les expressions algébriques.

Où il est à remarquer que par a², ou b³, ou semblables, je ne conçois ordinairement que des lignes toutes simples, encore que pour me servir des noms usités en l'algèbre je les nomme des carrés ou des cubes, etc.

Il est aussi à remarquer que toutes les parties d'une même ligne se doivent ordinairement exprimer par autant de dimensions l'une que l'autre, lorsque l'unité n'est point déterminée en la question, comme ici a³ en contient autant que ab² ou b³ dont se compose la ligne que j'ai nommée racine cubique de a³ – b³ + ab² ;
mais que ce n'est pas de même lorsque l'unité est déterminée, à cause qu'elle peut être sous-entendue partout où il y a trop ou trop peu de dimensions : comme s'il faut tirer la racine cubique de a²b² – b, il faut penser que la quantité a²b² est divisée une fois par l'unité, et que l'autre quantité b est multipliée deux fois par la même unité.

La constance C = 1 est utilisée ci-dessus pour respecter la règle des homogènes.
On multiplie ou on divise par l'unité pour trouver la même dimension dans tous les termes.

La Géométrie - Chapitre premier - Page 300

À la fin du paragraphe, Descartes fait de la pédagogie :
Au reste, afin de ne pas manquer à se souvenir des noms de ces lignes, il en faut toujours faire un registre séparé à mesure qu'on les pose ou qu'on les change, écrivant par exemple :
AB 1, c'est-à-dire AB égal à 1, en utilisant comme symbole de l'égalité le signe , déformation de la diphtongue de ce mot en latin : æquare. Nous remplacerons le signe par le signe =.
GH = a.
BD = b, etc.

Avec Descartes, les « lignes géométriques » prennent le statut de « variables réelles ».

Comment il faut venir aux équations qui servent à résoudre les problèmes

Avec pédagogie, Descartes expose sa méthode :
  – « nommer » les différentes lignes d'une figure,
  – les classer en connues et inconnues,
  – mettre en équation et résoudre ces équations.

Ainsi, voulant résoudre quelque problème, on doit d'abord le considérer comme déjà fait, et donner des noms à toutes les lignes qui semblent nécessaires pour le construire, aussi bien à celles qui sont inconnues qu'aux autres.

Descartes utilisera le premier les lettres du début de l'alphabet a, b, c, d… pour les lignes connues et celles de la fin pour les lignes inconnues x, y, z.

Puis, sans considérer aucune différence entre ces lignes connues et inconnues, on doit parcourir la difficulté selon l'ordre qui montre le plus naturellement de tous en quelle sorte elles dépendent mutuellement les unes des autres, jusqu'à ce qu'on ait trouvé moyen d'exprimer une même quantité en deux façons, ce qui se nomme une équation ; car les termes de l'une de ces deux façons sont égaux à ceux de l'autre.

Une des nouveautés de Descartes :

Et on doit trouver autant de telles équations, qu'on a supposé de lignes, qui étaient inconnues.

Ou bien, s'il ne s'en trouve pas tant, et que nonobstant on n'omette rien de ce qui est désiré en la question, cela témoigne qu'elle n'est pas entièrement déterminée.

Et lors on peut prendre à discrétion des lignes connues pour toutes les inconnues auxquelles ne correspond aucune équation.

Après cela, s'il en reste encore plusieurs, il se faut servir par ordre de chacune des équations qui restent aussi, soit en la considérant toute seule, soit en la comparant avec les autres, pour expliquer chacune de ces lignes inconnues, et faire

La Géométrie - Chapitre premier - Page 301

ainsi, en les démêlant, qu'il n'en demeure qu'une seule égale à quelque autre qui soit connue, ou bien dont le carré, ou le cube, ou le carré de carré, ou le sursolide (puissance 5), ou le carré de cube, etc., soit égal à ce qui se produit par l'addition ou soustraction de deux ou plusieurs autres quantités, dont l'une soit connue, et les autres soient composées de quelques moyennes proportionnelles entre l'unité et ce carré, ou cube, ou carré de carré, etc., multipliées par d'autres connues.

Ce que j'écris en cette sorte :

z = b,
ou z² = – az + b²,
ou z³ = + az² + b²z – c³,
ou z⁴ = az³ – c³z + d⁴, etc (Schooten).

C'est-à-dire z, que je prends pour la quantité inconnue, est égale à b ; ou le carré de z est égal au carré de b moins a multiplié par z ; ou le cube de z est égal à a multiplié par le carré de z plus le carré de b multiplié par z moins le cube de c ; et ainsi des autres.

Et on peut toujours réduire ainsi toutes les quantités inconnues à une seule, lorsque le problème se peut construire par des cercles et des lignes droites, ou aussi par des sections coniques, ou même par quelque autre ligne qui ne soit que d'un ou deux degrés plus composée.

Humour de Descartes : Je n'explique pas, pour ne pas vous ôter le plaisir d'apprendre !

Mais je ne m'arrête point à expliquer ceci plus en détail, à cause que je vous ôterais le plaisir de l'apprendre de vous-même, et l'utilité de cultiver votre esprit en vous y exerçant, qui est à mon avis la principale qu'on puisse

5. L'équation du second degré

Les Babyloniens, au deuxième millénaire avant J.-C., savaient trouver les solutions positives des équations du second degré avec la formule algébrique.
Ces formules ont été ignorées par les Égyptiens et les Grecs et réintroduites par Diophante au IV^e siècle et transmises à l'Occident par le mathématicien Al-Harizmi au IX^e siècle.

La Géométrie - Problèmes plans - Page 302

tirer de cette science.

Son dessein est que ses ennemis (comme Roberval) ne puissent pas profiter de ses explications :

Aussi que je n'y remarque rien de si difficile que ceux qui seront un peu versés en la Géométrie commune et en l'algèbre, ait qui prendront garde à tout ce qui est en ce traité, ne puissent trouver.

Dans sa lettre à Mersenne du 20 avril 1646, Descartes se justifie : « Seulement y ai-je omis (dans La Géométrie) quantité de choses, qui auraient pu servir à la rendre plus claire, ce que j'ai fait à dessein, et je ne voudrais pas y avoir manqué. »

C'est pourquoi je me contenterai ici de vous avertir que, pourvu qu'en démêlant ces équations, on ne manque point à se servir de toutes les divisions qui seront possibles, on aura infailliblement les plus simples termes auxquels la question puisse être réduite.

Quels sont les problèmes plans

Et que si elle peut être résolue par la Géométrie ordinaire, c'est-à-dire en ne se servant que de lignes droites et circulaires tracées sur une superficie plate, lorsque la dernière équation aura été entièrement démêlée, il n'y restera tout au plus qu'un carré inconnu, égal à ce qui se produit de l'addition ou soustraction de sa racine multipliée par quelque quantité connue, et de quelque autre quantité aussi connue.

Les problèmes plans sont ceux qui se ramènent à la résolution d'une équation du deuxième degré,
que Descartes réduit à la forme : z² = ± a z ± b², a et b étant positifs.
Il en représente les solutions positives par un segment.

Comment ils se résolvent

Et lors cette racine, ou ligne inconnue, se trouve aisément.

Équation z² = a z + b²

Cas où l'équation du second degré n’a qu'une racine positive, car Descartes ignore les nombres négatifs.
Cette racine est respectivement la longueur MO ou la longueur MP, selon que la somme des deux racines est positive ou négative.

La justification repose sur la notion de puissance du point M par rapport au cercle.

Car si j'ai par exemple

z² = az + b²,

je fais le triangle rectangle NLM, dont le côté LM est égal à b, racine carrée de la quantité connue b², et l'autre LN est a, la moitié de l'autre quantité connue qui était multipliée par z, que je suppose être la ligne inconnue ; puis prolongeant MN, la base de ce triangle (à l'époque, on prenait l'hypoténuse comme base d'un triangle rectangle),

Page 303 (ci-dessous)

jusqu'à O, en sorte qu'NO soit égale à NL, la toute OM est z, la ligne cherchée.
Et elle s'exprime en cette sorte : (OM = z = ON + MN)

.

Télécharger la figure GéoPlan eq_2de_1.g2w

Commentaires : z² = ± a z + b²

Équations z² = a z + b² et z² =  – a z + b² ayant une seule racine positive

Descartes fait une seule figure pour résoudre les deux types d'équations : z² = ± a z + b². Le coefficient constant b² est élevé au carré pour rendre l'équation homogène.

Les calculs utilisent la puissance d'un point par rapport à un cercle, notion élémentaire disparue de l'enseignement français au lycée.
La puissance d'un point M, par rapport au cercle de centre N et de rayon NO = a, est le produit MO × MP, où une sécante issue de M coupe le cercle en O et P.
Cette puissance est constante lorsque la droite varie. Elle est égale au carré b² de la longueur b d'une tangente ML au cercle, issue de M.
La puissance est aussi égale à la différence du carré de la distance du point au centre du cercle moins le carré du rayon.

La méthode de Descartes ne lui fait chercher que la « vraye » racine positive de ces équations z (z ± a) = b² (la « fausse » solution négative ne l'intéresse pas).

On montre facilement que MO × MP = (MN + NO) × (MN – NO) = MN² – NO² = LM² = b².
MO et MP = MO – a sont respectivement les solutions positives des équations z² – a z = b² et z² + az = b².

Équation z² = a z + b²

Vérifions que z = MO est la racine de la première équation. En effet, MP = MO – a. Comme MO × MP = b², on a z(z–a) = b² et on trouve la solution de z² – a z = b².

Calculons cette racine MO. On a : MO = MN + ON = MN + a, donc MN = z – a.
Le théorème de Pythagore, dans le triangle rectangle LMN, d'hypoténuse MN et de petits côtés NL = a et LM = b, permet d'écrire :
MN² = NL² + LM² =  + b², soit MN = z – a = , le segment MO de longueur représente bien la racine positive de l'équation z² = a z + b².

Équation z² = – a z + b²

Vérifions de même que z = MP est la racine de la deuxième équation. En effet, MO = MP + a. Comme MO × MP = b², on a (z+a)z = b² et on trouve la solution de z² + a z = b².
Calculons MP = MN – NP, donc MN = z + a, soit MN = z + a = ,
le segment MP de longueur 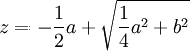représente la racine positive de l'équation z² = – a z + b².

Équation ayant deux racines positives : z² = az – b²

Cas où les longueurs MQ et MR sont les deux racines, positives, d’une équation.

Lorsque b ≤ a, nous utilisons encore la puissance du point M par rapport au cercle de centre N et de rayon a, qui est ML² = MQ × MR.

Cette propriété se démontre en introduisant le milieu I de QR et en utilisant le théorème de Pythagore dans le triangle rectangle NIR.
MQ × MR = (MI – IR) × (MI + IR) = MI² – IR² = NR² – IR² = NI² = ML² = b².

Or MQ + MR = a, donc si z est une des longueurs, l'autre est a – z,
on a bien MQ × MR = z(a–z) = b² et z est une des solutions de l'équation az – z² = b².

Dans le triangle rectangle NIR on a : IR² = NR² – NI² =  – b² = .

Première solution

Si z = MR on a IR = MR – IM = z – a donc  IR² = (z – a)² = ,
finalement z – a = , d'où 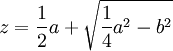est bien une des solutions de l'équation z² = az – b².

Deuxième solution

De même, si z = MQ on a IQ = IM – MQ =  a – z et IQ² = ( a – z)² = IR² = .

Finalement a – z =  et 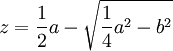est l'autre solution.

Figure : Équation z² = 10 z – 3²

Télécharger la figure GéoPlan eq_2de_2.g2w

La Géométrie - Chapitre premier - Page 303

Équation y² = – ay + b²

Que si j'ai y² = – ay + b², et qu'y soit la quantité qu'il faut trouver, je fais le même triangle rectangle NLM, et de sa base MN j'ôte NP égale à NL, et le reste PM est y la racine cherchée. De façon que j'ai

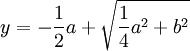
Équation x⁴ = – ax² + b²

Et tout de même si j'avais x⁴ = – ax² + b².
PM serait x² et j'aurais

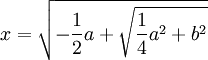
et ainsi des autres.

Équation z² = az – b²

Remarque : Victor Cousin propose une figure 4 symétrique à celle ci-contre, avec permutation des points L et M, le texte est alors modifié en conséquence.

Enfin si j'ai z² = az – b² ; je fais NL égale à a, et LM égale à b comme devant, puis, au lieu de joindre les points M N je tire MQR parallèle à LN. Et du centre N par L ayant décrit un cercle qui la coupe aux points Q et R, la ligne cherchée z est MQ, ou bien MR, car en ce cas elle s'exprime en deux façons, à savoir

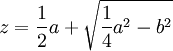
et .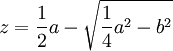

Et si le cercle, qui ayant son centre au point N, passe par le point L, ne coupe ni ne touche la ligne droite MQR, il n'y a aucune racine en l'Équation, de façon qu'on peut assurer que la construction du problème proposé est impossible.

La Géométrie - Chapitre premier - Page 304

Au reste, ces mêmes racines se peuvent trouver par une infinité d'autres moyens, et j'ai seulement voulu mettre ceux-ci, comme fort simples, afin de faire voir qu'on peut construire tous les Problèmes de la Géométrie ordinaire sans faire autre chose que le peu qui est compris dans les quatre figures que j'ai expliquées.

Les coniques et nombre de leurs propriétés souvent subtiles étaient connues des Grecs. La « vraie méthode » de Descartes remplace la géométrie métrique par une équation du second degré et permet aux mathématiques de faire un progrès décisif.

Ce que je ne crois pas que les Anciens aient remarqué ; car autrement ils n'eussent pas pris la peine d'en écrire tant de gros livres où le seul ordre de leurs propositions nous fait connaître qu'ils n'ont point eu la vraie méthode pour les trouver toutes, mais qu'ils ont seulement ramassé celles qu'ils ont rencontrées.