Descartes et les Mathématiques

Paraboles

Tangentes, normales, foyer et directrice, enveloppe, développée, lieu de points, tableau de fils, tourniquette, théorèmes de Poncelet, de Pascal.

Sommaire

1. Méthode de Torricelli

2. Sous-normale

3. Foyer et directrice

4. Cordes et tangentes

    La parabole chez les Anciens

5. Tourniquette

6. Tangente et lieu géométrique

7. Parabole et composition de fonctions

8. Enveloppe - Tableau de fils

9. Développée

10. Construction pratique

11. Lieu de l'orthocentre

12. Lieu de points

13. Théorèmes de Poncelet

14. Théorème de Pascal

Pont suspendu de Mallemort sur la Durance

Équation de la parabole

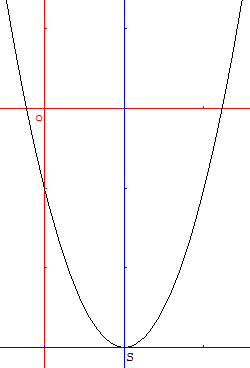
La parabole est la courbe d'équation cartésienne : y = f(x) associée
au trinôme du second degré f(x) = ax² + bx + c.

Équation réduite dans un repère ayant pour origine le sommet de la parabole

La forme canonique du trinôme f(x) = a[{x + }² – ] où Δ = b² – 4ac,
permet avec le changement de variable X = x +  et Y = y + 
d'obtenir la forme réduite Y = aX² dans le repère d'origine le sommet S(– , – ) de la parabole.

Ci-contre : graphique avec GéoPlan

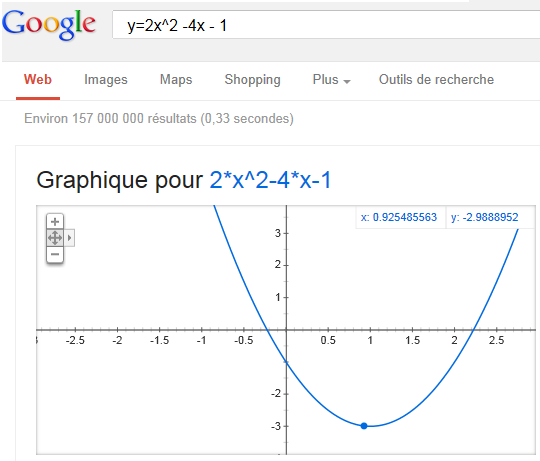
Parabole d'équation y = 2x² – 4x – 1

Avec GeoGebra
Feuille de travail : parabole

Figure interactive dans GeoGebraTube : parabole définie par ses coefficients

Graphique avec Google

Taper la formule du trinôme x^2 – 4x – 1 ou bien l'équation cartésienne dans le moteur de recherche :

1. Méthode de Torricelli

Evangelista Torricelli : physicien et géomètre italien (1608-1647) : a connu à l'âge de 20 ans Galilée, et sous son influence a étudié le mouvement parabolique des projectiles. Il découvrit la quadrature de la cycloïde en 1638 puis son aire en 1644. Il inventa le baromètre en 1643.

Équation de la tangente à la parabole en A

Soit P la parabole d'équation y = f(x) = k x², dans un repère orthogonal (O, , ).

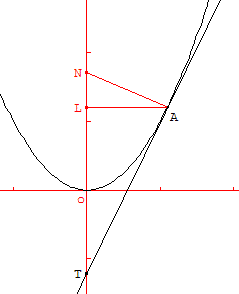
Pour tout point A d'abscisse a non nulle Torricelli propose la méthode suivante :

  • construire le projeté orthogonal L de A sur l'axe des ordonnées,
  • construire le symétrique T de L par rapport à O,
  • la droite (AT) est la tangente à la parabole P au point A.

La tangente a donc pour équation y = f’(a) x – f(a).

On dit que [LT] est la sous-tangente : la sous-tangente à la parabole a un milieu fixe : le point O.

2. Sous-normale

La perpendiculaire, au point de contact A, à la tangente coupe l'axe des ordonnées en N.
La parallèle à l'axe des abscisses, passant par A, coupe l'axe des ordonnées en L.
Quel que soit le point A, distinct de O, le segment [LN] a une longueur constante.
[LN] est appelé sous-normale. Sa longueur est le paramètre p = LN = de la parabole d'équation :
y = k x² = x²(si k > 0).

Télécharger la figure GéoPlan nor_para.g2w

3. Foyer et directrice

Étant donné une droite (d) et un point F non situé sur (d).
La distance de F à (d) est le paramètre p = FK (où K est la projection orthogonale de F sur d).

Une parabole est l'ensemble (P) des points équidistants du foyer F et de la directrice (d).

C'est donc l'ensemble des points M tels que MF = MH,
avec H la projection orthogonale de M sur (d).

Le point F est appelé le foyer de la parabole et la droite (d) la directrice.
Dans un repère (O, , ), où O est le milieu de [KF] et   parallèle à (d),
le point F a pour coordonnées (0, ), la directrice a pour équation y = − .

Le segment de tangente [MJ], déterminé par le point de contact et la directrice, est vu du foyer sous un angle droit (MFJ = 90°).

Télécharger la figure GéoPlan pa_foyer.g2w

Équation réduite

Dans un repère ayant pour origine le sommet de la parabole

Dans le repère d'origine le sommet, la parabole a pour équation réduite y = ax² = x², où a = , soit p = .

Le foyer F a pour coordonnées (0, ), la directrice a pour équation y = −.

Trouver le foyer et la directrice

À partir de l'équation canonique de la parabole.

La parabole d'équation y = ax² + bx + c a pour équation canonique : y = a[{x + }² – ] où Δ = b² – 4ac.

Dans le repère d'origine le sommet S(– , – ), le foyer a pour coordonnées F(– , – + ) et la directrice a pour équation y = – – .

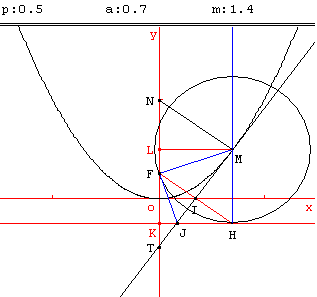
3.b. Cercles tangents à la directrice

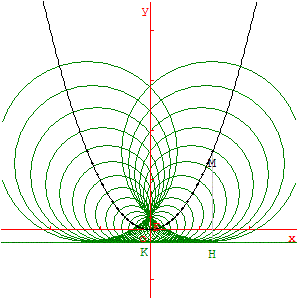
La parabole P est le lieu géométrique des centres M des cercles passant par le foyer F et tangents à la directrice (d).

La tangente en M à la parabole est la médiatrice de [FH]. La normale en M coupe l'axe (FK) de la parabole en N.

La sous-normale [LN] a une longueur constante égale au paramètre p = KF = LN. La tangente est la bissectrice intérieure de l'angle FMH. La bissectrice extérieure est (MN), bissectrice de l'angle FMy.

Un rayon focal issu de F se réfléchit en M sur la parabole et repart parallèlement à l'axe de la parabole, propriété utilisée dans les phares, radars ou antennes…

4. Cordes et tangentes

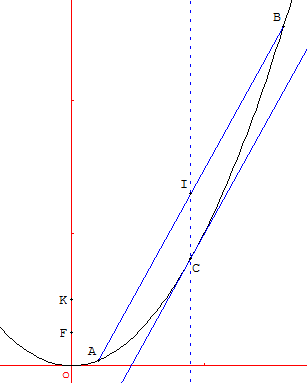
La tangente à la parabole parallèle à la corde [AB] a pour point de contact le point C dont l'abscisse est la moyenne des abscisses de A et B.

Le coefficient directeur u de (AB) est : u = =  f’(c) = k (a + b).

{parabole d'équation y = k x²}

Soit I le milieu du segment [AB] : la droite (CI) est parallèle à l'axe de la parabole (oy). Cette droite est appelée diamètre de la parabole relativement à la corde [AB]. Le point C est le sommet de la parabole relativement à ce diamètre.

Remarque : pour l'axe focal, si K est le point de l'axe (oy) d'ordonnée le paramètre p = , on appelle aussi diamètre de la parabole le segment [oK], de longueur p.

Si le coefficient k est positif, le point C est en dessous du segment [AB]. La parabole (P) est une courbe convexe.

4.b. La parabole chez les Anciens

Les géomètres grecs n'avaient pas GéoPlan, ni GeoGebra…

Cathète

Ancien synonyme de ligne perpendiculaire : droite qui tombe perpendiculairement sur une autre droite ou sur une surface. Côté de l'angle droit d'un triangle rectangle.

Les anciens géomètres français, comme Descartes dans sa Géométrie, donnent le nom d'essieu à l'axe d'une courbe, appelé aussi cathète chez les « anciens Grecs ».

Latus rectum

Une corde qui passe par le foyer est une corde focale. Chez les Grecs, la corde focale perpendiculaire à l'axe est le côté droit de la parabole, on l'appelle aussi par son nom latin le latus rectum. Le paramètre p, demi-longueur du côté droit, est aussi nommé latus rectum.

Propriétés diamétrales des coniques

Si on coupe une conique par des droites parallèles, les milieux des cordes ainsi obtenues sont alignés, sur une droite appelée « un diamètre ».
Pour une parabole, les diamètres sont parallèles à l'axe.

4.c. Diamètre et côté droit

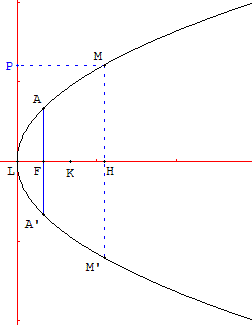
Si K est le point de l'axe (ox) d'abscisse le paramètre p = , le segment [LK], de longueur p, est le diamètre de la parabole.

Le foyer F est le milieu de [LK]. L'axe (LK) est l'essieu de la parabole.

La perpendiculaire en F à (LK) coupe la parabole en A et A’. Le segment [AA’], perpendiculaire à l'axe au foyer, est le côté droit (latus rectum) de la parabole, de longueur m = 2p.

De l'équation x = k y² = y², on trouve y² = 2px = mx.

Voir aussi : côté droit de l'ellipse

4.d. Quadrature d'un rectangle

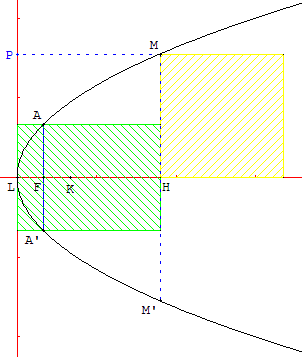
Certains appellent aussi latus rectum la corde [MM’],
[LH] est le diamètre relatif à cette corde.

Le rectangle, ayant pour côtés le latus rectum et [LH], a même aire que le carré de côté HM :
AA’ × LH = HM².
Les calculs des Anciens ressemblaient à HM² = m LH, depuis Descartes nous utilisons y² = mx.

5. Tourniquette sur une parabole

Cordes parallèles

Soit A, B, D et E quatre points distincts, d'abscisses respectives a, b, d et e, points situés sur la parabole P d'équation y = k x².

On peut déduire de la question précédente que la corde [AB] est parallèle à la corde [DE],
si et seulement si : a + b = d + e.

(Ces deux cordes sont parallèles à la tangente au point d'abscisse .)

Tourniquette

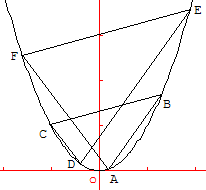
Tourniquette : ligne brisée formée par une suite de segments deux à deux parallèles tracés sur une figure comme un polygone ou une conique.

On choisit sur la parabole P quatre points A, B, C et D d'abscisses respectives a, b, c et d.

On construit deux points E et F sur la parabole tels que (DE) // (AB), puis (EF) // (BC).

On montre que le tourniquet se referme avec (FA) // (CD).

En effet, si e et f sont les abscisses des points E et F, on a :
a + b = d + e, car (AB) // (DC),
e + f = b + c, car (EF) // (BC).

En ajoutant membre à membre les deux égalités et en simplifiant par b + e, on trouve :
a + f = c + d ce qui prouve que (FA) // (CD).

6. Tangentes et lieu géométrique - Corde focale

Dans un repère orthonormé (O, , ), on note P la parabole représentative de la fonction :
f(x) = , de paramètre p = 2 et F le foyer de coordonnées F(0, 1).

Une droite (Δ) de coefficient directeur m passe par F et coupe P en A et B d'abscisses x₁ et x₂.

Les tangentes à la parabole (P) en A et B se coupent en I.

Objectif : trouver le lieu géométrique du point I lorsque la droite (Δ) pivote autour de F.

Définition : La courbe orthoptique d'une parabole est le lieu des points d'où l'on peut mener deux tangentes à la parabole perpendiculaires entre elles, autrement dit le lieu des points d'où l'on « voit » la parabole sous un angle droit.
C'est la directrice de la parabole.

Les deux tangentes sont perpendiculaires. Le lieu est donc la courbe orthoptique de la parabole.

Démonstration « analytique »

• Montrer que la droite (Δ) a pour équation y = mx + 1.
• Vérifier que x₁ et x₂ sont les deux solutions distinctes de l'équation du second degré :
  x² – 4 m x – 4 = 0.
• Écrire en fonction de x₁ l'équation de la tangente en A à la parabole P et en fonction de x₂ l'équation de la tangente en B.
• Montrer que ces deux tangentes sont sécantes au point I de coordonnées : (, ).
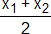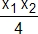• Trouver les coordonnées de I en fonction de m et vérifier que I est un point de la directrice (d) d'équation y = −1.

Démonstration en « géométrie pure »

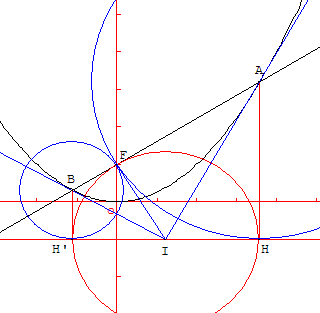
P est une parabole de foyer F et de directrice (d).

Soit (Δ) une droite, passant par le point F, distincte de l'axe (Oy).

Analyse : si A est un point de la parabole situé sur la droite (Δ), ce point équidistant de F et de (d) est le centre d'un cercle passant par F et tangent à (d). La normale à (Δ) passant par F est tangente à ce cercle. Cette normale coupe la directrice en I. Les demi-droites [IH) et [IF) sont les deux tangentes au cercle issues de I, les segments sont égaux : IF = IH. Le point H est sur le cercle de centre I, passant par F.

Synthèse : la normale à (Δ) passant par F coupe la directrice en I. Le cercle de centre I, passant par F, coupe la directrice en deux points H et H’. Les normales à (d) passant par H et H’ coupent (Δ) en deux points A et B. AH = AF donc A est sur la parabole P et (AI), médiatrice de [FH] est tangente à la parabole. De même (BI), médiatrice de [FH’], est l'autre tangente à la parabole.

[AB] est une corde focale de la parabole P. Les tangentes en A et B se coupent en I sur la directrice (d). Ces deux tangentes (IA) et (IB) sont les bissectrices en I des droites (d) et (IF) ; elles sont donc orthogonales.

Télécharger les figures GéoPlan tan_cord.g2w,   tan_cor2.g2w

7. Parabole et composition de fonctions

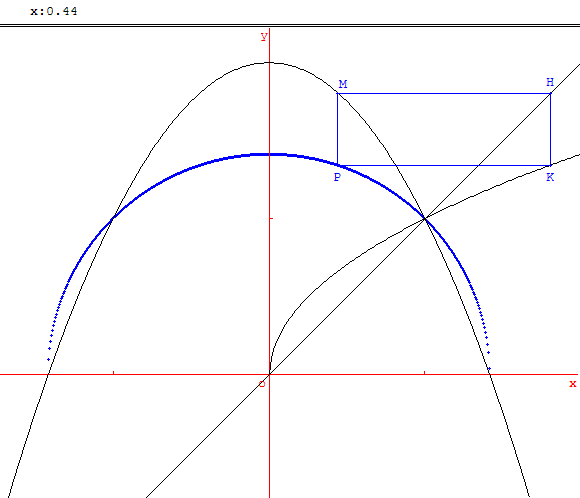
f est la fonction définie sur [0, +∞] par f(x) = 
et g la fonction définie sur R par g(x) = 2 – x².

M est un point d'abscisse x de (P), représentation graphique de g ; H est le point de la droite (d) d'équation y = x ayant la même ordonnée que M.

Lorsque la construction est possible, on note K le point de la courbe (C), représentation graphique de f, ayant la même abscisse que H.

P est le quatrième sommet du rectangle MHKP.

En déplaçant le point M vérifier que le point K existe que lorsque x est dans l'intervalle I = [–  ; ]. Ce point K appartient à l'arc des points de la courbe (C) dont les abscisses sont inférieures à 2.

Les coordonnées des sommets du rectangle sont :
M(x, 2 – x²) ; H(2 – x², 2 – x²) ; K(2 – x², ) et P(x, ).

OP² = 2. L'ensemble des points P, d'ordonnées positives, est le demi-cercle de centre O est de rayon .

La fonction k définie sur I, qui à x associe l'ordonnée de P, est la fonction composée k = f o g.

8. Enveloppe

Soit un point F et une droite (d) étant considérés comme fixes,
un point M variable sur (d) et (m) la médiatrice de [FM].

En répétant les constructions lorsque le point M varie sur la droite (d), on voit apparaître l'enveloppe de la famille des médiatrices (m) ; courbe non tracée déterminée par ses tangentes.

La courbe est la parabole de foyer F et de directrice (d).

Si au lieu d'une droite (d), on avait tracé un cercle (c), on aurait obtenu de cette façon une ellipse ou une hyperbole.

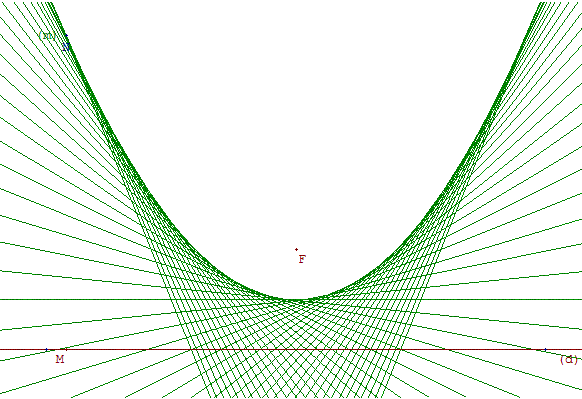
Le mode trace de GéoPlan permet de mémoriser le tracé des tangentes.

8.b. Construction par pliage

Sur une feuille, tracer un point F et une droite (d). Amener par pliage le point F sur la droite (d), marquer le pli et déplier.
En répétant un grand nombre de fois, en variant la position sur (d), on obtient la parabole.

Le pliage est simplifié en prenant pour directrice (d) le bord de la feuille. Il suffit alors de rabattre le point F en diverses positions de ce bord.

8.c. Tableau de fils

La réalisation de tableaux de fils et clous est maintenant un classique des travaux manuels.

Nous allons à l'aide de GéoPlan la simuler pour obtenir une parabole en réalisant un réseau de tangentes où les segments représentent des fils tendus entre deux clous.

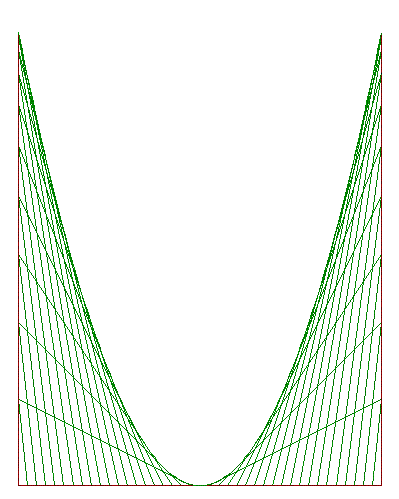
Dans un repère orthonormé (O, , ), on note P la parabole représentative de la fonction :

f(x) = étudiée sur l'intervalle [–10, 10].

Comme nous l'avons vu au paragraphe 1., la méthode de Torricelli montre que la tangente au point d'abscisse n a pour équation y = f’(n) x – f(n).

Cette tangente coupe l'axe (Ox) au point A d'abscisse .

La tangente coupe, si n > 0, la droite verticale d'équation x = 10 au point B d'ordonnée
10 f’(n) – f(n) = 10 – ,
ou si n < 0, la droite verticale d'équation x = −10 au point B d'ordonnée :
–10 f’(n) – f(n).

Le mode trace permet de dessiner 41 segments à partir de « points A » régulièrement répartis sur le bord horizontal et, sur chaque bord vertical, de 10 autres « points B » dont les ordonnées, calculées ci-dessus, sont :

9. Développée

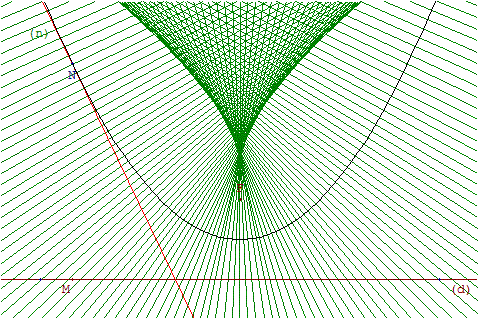
Soit un point F et une droite (d) étant considérés comme fixes, foyer et directrice d'une parabole, un point M variable sur (d) et (t) la médiatrice de [FM] tangente en N à la parabole.

Au point N, traçons la normale (n) à la parabole, perpendiculaire à (t).

L'objectif est de déterminer l'enveloppe de la famille des normales (n) obtenues lorsque le point M varie sur la droite (d).

La courbe obtenue est la développée de la parabole.

Télécharger la figure GéoPlan develope.g2w

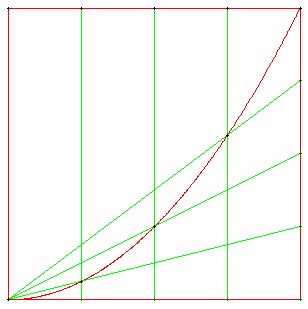
10. Construction pratique

Construire point par point une parabole dont on connaît le sommet, l'axe de symétrie et un point.

À partir d'un point M de la courbe ayant pour projection P sur la tangente au sommet on partage les segments [OP] et [PM] en quatre parties égales. Les points M₁, M₂, M₃ construits ci-dessus sont situés sur la parabole et on complète avec les symétriques.

Si la parabole a pour équation y = k x²,
soit pour M : MP = k OP²,
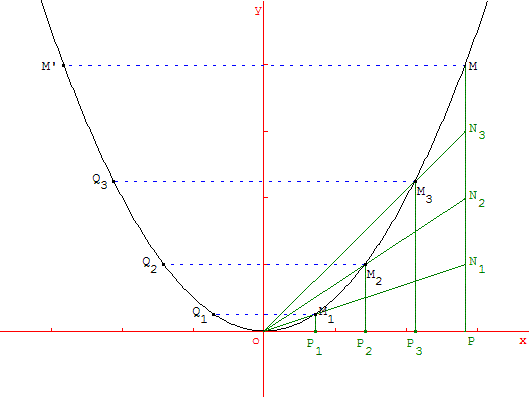
on en déduit, par exemple, que pour M₃(x, y) on a :
x = OP₃ = OP,
et y = P₃M₃ = PN₃ = × MP
y = k OP² = k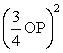 = k OP₃² = k x² vérifie l'équation.

La construction peut aussi se faire à partir d'un des points M₁, M₂ ou M₃ pour trouver des points de la parabole au-delà du point connu.

Cette méthode est valable pour d'autres partages des segments [OP] et [PM] en parties égales.

10.b. Construction, dans un géoplan 5 × 5

À la manière des compagnons bâtisseurs du Moyen-Âge

Olympiades 2008 - Toulouse

Comment les compagnons ont-ils pu partager les côtés du carré en quatre parties égales ?

Indications

Le partage du carré en 2 se fait avec deux médiatrices, tracé facilité en remarquant qu'elles passent par le milieu O du carré, point d'intersection des deux diagonales.
Terminer le partage en 4 avec les diagonales des 4 petits carrés obtenues en partageant le grand.

La planche à clous comme géoplan

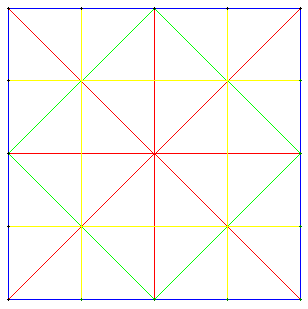
10.c. Partage en quatre d'un carré

Un chemin a été ébauché sur cette figure.
Que dire de la forme de ce chemin ? 

Les points d'intersection de cette figure pour les abscisses x = 0, ,, , 1 ;
sont situés sur les obliques d'équations y = ax, avec le coefficient directeur a = x.

On a donc y = x², équation d'une parabole.

L'idée des compagnons serait de poursuivre en partageant en 8, puis en 16, etc.

C'est possible et le tracé sera encore plus précis.

11. Lieu de l'orthocentre

11.a. La droite est parallèle au côté opposé à ce sommet

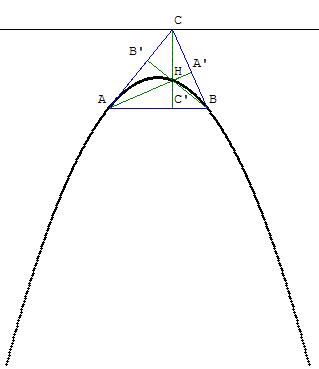
Recherche du lieu de l'orthocentre d'un triangle lorsque l'un des sommets se déplace sur une droite.

Si (d) est une droite parallèle à (AB), distincte de (AB), le lieu de l'orthocentre H, quand le sommet C parcourt la droite (d), est une courbe passant par A et B. Cette courbe est symétrique par rapport à la médiatrice de [AB]. On va montrer que c'est une parabole.

Conjecture avec GéoPlan

Limiter les déplacements de C à un segment de la droite (d) pour tracer le lieu géométrique :

C point libre sur un segment

Démonstration en géométrie analytique

Utilisons un repère (O, , ) centré en O milieu de [AB] tel que :
= et que soit un vecteur directeur de la médiatrice de [AB].

Les coordonnées des points sont alors A(–1, 0) ; B(1, 0) ; C(x, γ) et H(x, y) car H étant l'orthocentre du triangle ABC, C et H ont même abscisse x.
Pour simplifier les calculs, choisir γ = 1.

AH étant orthogonal à CB, le produit scalaire . = 0.

Les coordonnées des vecteurs sont (1 + x, y) ; (1 – x, – γ).

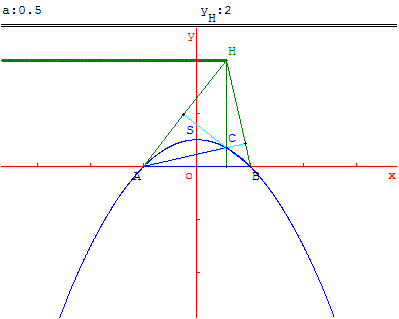
On obtient finalement avec la formule analytique du produit scalaire :

XX’ + YY’ = (1 + x) (1 – x) – γ y = 0,
soit y =       γ ≠ 0.

Cette équation prouve que H se déplace sur une parabole passant par A et B et, qui plus est, que le lieu de H est toute la parabole, étant donné que x décrit R.

Réciproquement, comme l'orthocentre du triangle ABH est le point C, on peut montrer que si C se déplace sur une parabole passant par A et B, d'axe de symétrie la médiatrice de [AB], alors le lieu de l'orthocentre est une droite parallèle à (AB).

Rétroliens ( backlink) : lieux géométriques niveau lycée
Ressources mathématiques pour l'enseignement de base au Liban

11.b. Lieu de point

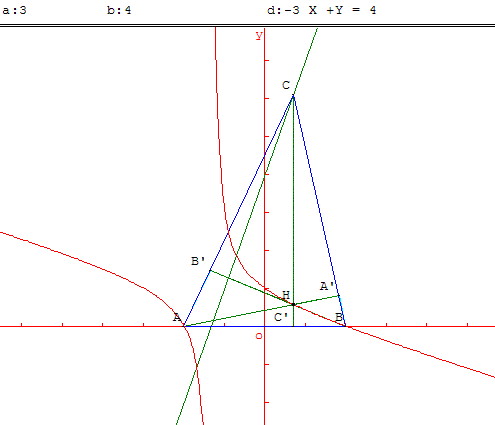
Le point C décrit une droite qui coupe (AB) en D distinct de A et B

Dans le repère du paragraphe a précédent, le point C se déplace sur une droite (d) d'équation :

y = α x + β avec α ≠ 0 et β ≠ 0.

Il a donc pour coordonnées C(x, α x + β). Les coordonnées des autres points sont toujours A(–1, 0) ; B(1, 0) et H(x, y).

Les coordonnées des vecteurs sont : (1 + x, y)  ;
(1 – x, –(α x + β)).

On trouve finalement avec la formule analytique du produit scalaire . nul :

(1 + x) (1 – x) – y (α x + β) = 0,
soit y = .

On obtient une hyperbole.

11.c. Le point C décrit une courbe d'équation y = f(x)

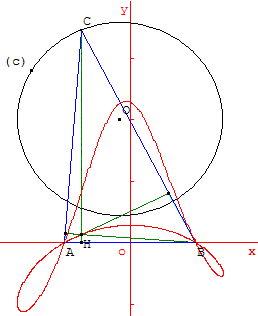
Jean Fages fait remarquer que les calculs réalisés au-dessus permettent d'affirmer que le lieu de H est la courbe d'équation

y = .

Exemple : point C variable sur un cercle.

Cas particulier où le cercle passe par A et B : voir lieu géométrique dans le triangle

Télécharger les figures GéoPlan dr_ortho.g2w,

    pa_ortho.g2w,  

    ce_ortho.g2w

Retrouver ce lieu à l'épreuve pratique 2007

La géométrie à l'épreuve pratique de terminale S avec GéoPlan et GéoSpace.

12. Parabole comme lieu de points

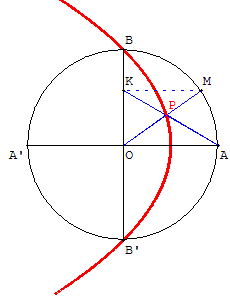
Soit un cercle fixe (c) de centre O, deux diamètres perpendiculaires [AA’] et [BB’] et M un point qui décrit le cercle sauf les points A et A’.

On projette orthogonalement le point M sur le segment [BB’] en K et on appelle P le point d'intersection des droites (OM) et (AK).

Montrer que le lieu du point P est la parabole de foyer O et directrice (D), tangente au cercle en A, privée de son sommet.

13. Théorèmes de Poncelet

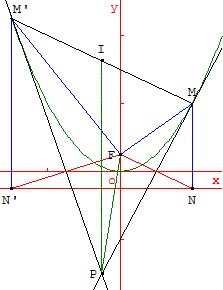
M et M’ sont deux points de la parabole.
Les tangentes à la parabole en M et M’ se rencontrent en P.

Si le point I est le milieu de [MM’], la droite (PI) est parallèle à l'axe de la parabole.

Premier théorème de Poncelet : (FP) est la bissectrice de l'angle MFM’.

Deuxième théorème de Poncelet : les angles FPM et IPM’ sont égaux. Les droites (PF) et (PI) sont isogonales par rapport aux droites (PM) et (PM’).

14. Théorème de Pascal

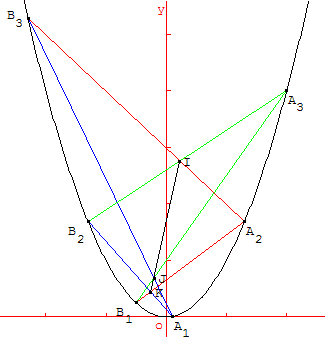
Théorème de Pascal dit de l'hexagramme mystique :

Pour un hexagone inscrit dans une conique, le théorème de Pascal affirme que les points d'intersection des côtés opposés de l'hexagone, s'ils existent, sont alignés.

La droite que forme cet alignement est appelée droite de Pascal. La figure est appelée hexagramme mystique.

À l'aide du théorème de Ménélaüs,

Pascal a démontré ce théorème pour un cercle, puis l'a généralisé à n'importe quelle conique, sachant que c'est une propriété projective, et qu'une propriété projective du cercle est valable pour toute conique.

Le théorème de Pappus-Pascal l'applique aussi à une conique dégénérée en deux droites.

La réciproque de ce théorème est vraie également : si les trois points d'intersection des côtés opposés d'un hexagone sont alignés alors l'hexagone est inscrit dans une conique.

En géométrie projective, un des trois points où les trois points peuvent être des points à l'infini.

Application à la parabole

On choisit, sur une parabole, six points A₁, A₂, A₃ et B₁, B₂, B₃, d'abscisses respectives a₁, a₂, a₃ et b₁, b₂, b₃.

Dans l'hexagramme A₁B₂A₃B₁A₂B₃, les côtés opposés (A₂B₃) et (A₃B₂) se coupent en I, (A₁B₃) et (A₃B₁) se coupent en J, (A₁B₂) et (A₂B₁) se coupent en K.

Les points I, J, K sont alignés sur la droite de Pascal (IJ).

Table des matières

Dans d'autres pages du site

Paraboles en L

Aire maximum
Approche géométrique d'une tangente
Histoires de toit - voûte parabolique
Quadrature par la méthode d'Archimède
Crible géométrique de Matiiassevitch

Équations du second degré

Minimum-maximum

Avec GeoGebra : Parabole ; Hyperbole

Coniques à centre

Tangente à une courbe

Problèmes de construction en 1^ère L : pentagone

Nombres constructibles : grands problèmes de la géométrie grecque

Épreuve pratique en TS

2007 : Tangente à une parabole

2008 : Points équidistants d'une droite et d'un point

            Cercles et paraboles

2009 : Propriétés de la parabole

Google friendly

Téléchargement

 Télécharger parabole.doc : ce document au format « .doc »

Télécharger parabole.pdf : ce document au format « .pdf »

Google considère l'URL comme une erreur de type "soft 404"

Rétrolien ( backlink)

Villemin Gérard : Parabole