 Descartes et les Mathématiques
Descartes et les Mathématiques
Les problèmes de clôture mathématique
Sommaire
3. Tourniquette sur un polygone
Tourniquette sur une parabole
Reconstituer un triangle
D'un triangle, il ne reste que les milieux des côtés,
retrouver le triangle : le triangle, c'est le pied
Construire un triangle connaissant ses médianes : droites remarquables du triangle
« Le triangle orthique est l'unique trajectoire de billard triangulaire qui se ferme ».
1. Reconstituer un pentagone à partir des milieux

Retrouver un pentagone ABCDE à partir des milieux I, J, K, L et M de ses côtés ?
Trouver une solution
Le logiciel GéoPlan permet à partir de cinq milieux I, J, K, L, M et d'un sommet variable A1 de faire une conjecture pour une solution :
À partir du point A1, par symétrie, on trouve B’, C’ D’ et E’. Si le symétrique de E’ par rapport à M est A1, le pentagone A1B’C’D’E’ est une solution.
Dans la figure de gauche et, en général, ce n'est pas le cas et E’ a un symétrique A’, distinct de A1, et nous obtenons une ligne brisée.
Dans l'imagiciel en déplaçant le point A1 on s'aperçoit que son image A’ est obtenue par une transformation connue.
En effet, en plaçant le point A milieu de [A1A’], nous trouvons un point fixe indépendant de A1. Les points A1 et A’ sont symétriques par rapport à A. La composition de cinq symétries centrales est une symétrie.
Le point A est le sommet du pentagone que l'on reconstitue par les cinq symétries centrales.
![]() Télécharger la figure GéoPlan mon_044s.g2w
Télécharger la figure GéoPlan mon_044s.g2w
Dans GéoPlan, déplacer A1, le faire coïncider avec A’,
taper S pour visualiser/masquer le pentagone ABCDE solution.
Construction d'une médiane

Dans un pentagone ABCDE, intéressons-nous aux diagonales [AC] et [AD], de milieux respectifs P et Q.
Dans le triangle ABC, la droite des milieux (IJ) est parallèle à (AC) et IJ est égal à la moitié
de AC.
De même, dans le triangle ACD, la droite des milieux (QK) est parallèle à (AC), QK est égal à la moitié de AC.
Les segments [IJ] et [PK] sont alors parallèles et de même longueur. IJKQ est un parallélogramme.
De même, dans les triangles AED et ACD, les segments des milieux [ML] et [PK] sont parallèles et de même longueur, égale à la moitié de AD.
MLKP est un parallélogramme.
On retrouve la configuration du théorème de la médiane du triangle ADC : la diagonale [KA] du parallélogramme APKQ vérifie les relations vectorielles :
![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() .
.
Pour reconstruire un pentagone à partir des milieux des côtés il suffit de construire le sommet A tel que ![]() =
= ![]() +
+ ![]() .
.
Procéder de la façon suivante : tracer le point P quatrième sommet du parallélogramme MLKP et le point Q quatrième sommet du parallélogramme IJKQ. Le point A est alors le quatrième sommet du parallélogramme PKQA.
Il suffit ensuite de reconstituer les autres points du pentagone symétriques de A par rapport aux milieux I, P, Q, M.
Construction

Tracer le point S tel que ![]() =
= ![]() ,
LKJS est un parallélogramme et
,
LKJS est un parallélogramme et ![]() =
= ![]() .
.
En introduisant S dans des relations de Chasles pour le calcul de la médiane, on trouve :
![]() = (
= (![]() +
+ ![]() ) + (
) + (![]() +
+ ![]() ).
).
![]() −
− ![]() =
= ![]() + (
+ (![]() +
+ ![]() ).
).
Le premier terme est ![]() −
− ![]() =
= ![]() =
= ![]() +
+ ![]() et en simplifiant on a :
et en simplifiant on a :
![]() =
= ![]() +
+ ![]() , d'où le parallélogramme ISMA.
, d'où le parallélogramme ISMA.
Nous avons alors la construction suivante avec un seul point intermédiaire :
Si IJKLM est le pentagone des milieux, on accroche en J un segment JS de même direction, même sens (!) et même longueur que PQ.
La démonstration précédente assure que le quatrième sommet A du parallélogramme ISMA est un des sommets du pentagone cherché qu'on restitue par symétries successives par rapport aux quatre milieux I, J, K, L.
![]() Télécharger la figure GéoPlan mon_044b.g2w, la figure GéoPlan mon_044p.g2w
Télécharger la figure GéoPlan mon_044b.g2w, la figure GéoPlan mon_044p.g2w
2. Reconstituer un quadrilatère

Comment retrouver un quadrilatère ABCDE à partir des milieux I, J, K et L de ses côtés ?
Trouver une solution
Le logiciel GéoPlan permet à partir de quatre milieux I, J, K, L et d'un sommet variable A de faire une conjecture pour une solution.
À partir du sommet A, par symétrie, on trouve B, C et D. Le symétrique de D par rapport à L devrait être A pour obtenir un quadrilatère. Sur notre figure et, en général, ce n'est pas le cas, D a pour symétrique A’, distinct de A, et nous obtenons une ligne brisée.
En déplaçant le point A on s'aperçoit que son image A’ est obtenue par une transformation connue et une aide à la solution est donnée par l'imagiciel en tapant sur la touche S :
C est l'image de A par la composition de deux symétries de centres I et J, c'est la translation de vecteur ![]() = 2
= 2 ![]() (En effet, dans le triangle ACB, AC est parallèle
à la droite des milieux IJ et égal au double de la longueur du segment).
(En effet, dans le triangle ACB, AC est parallèle
à la droite des milieux IJ et égal au double de la longueur du segment).

De même, A’ est l'image de C par la composition de deux symétries de centres K et L, c'est la translation de vecteur ![]() = 2
= 2 ![]() (remarquer que KL est une droite des milieux du triangle CA’D).
(remarquer que KL est une droite des milieux du triangle CA’D).
On passe de A à A’ par la composition des deux translations, c'est une translation de vecteur :
2 ![]() + 2
+ 2 ![]() = 2(
= 2(![]() +
+ ![]() )
= 2
)
= 2 ![]() .
.
D'où ![]() = 2
= 2 ![]() .
.
Déplacer les milieux et constater que la ligne brisée se referme lorsque I’ coïncide avec I :
![]() =
= ![]() : IJKL est un parallélogramme.
: IJKL est un parallélogramme.
![]() Télécharger la figure GéoPlan mon_044v.g2w
Télécharger la figure GéoPlan mon_044v.g2w
Une infinité de solutions

Le théorème de Varignon assure que IJKL doit être un parallélogramme pour que la construction soit possible.
En effet, dans le triangle ABC, le théorème des milieux permet de montrer que IJ est parallèle à la diagonale AC du quadrilatère et égal à sa moitié.
De même, LK est parallèle à AC et égal à sa moitié.
Dans ce cas une infinité de quadrilatères répondent à la question, on peut alors les tracer à partir de n'importe quel point A du plan et trouver de proche les autres points.
L'aire du quadrilatère ABCD est le double de l'aire du parallélogramme IJJK :
si les diagonales (AC) et (BD) de ABCD se coupent en O, le milieu de [OA] se trouve sur (IL) et l'aire du triangle AIL est égale à l'aire de OIL, de même Aire(BIJ) = Aire(OIJ), Aire(CJK) = Aire(OJK), Aire(DKL) = Aire(OKL).
![]() Télécharger la figure GéoPlan mon_044r.g2w
Télécharger la figure GéoPlan mon_044r.g2w
3. Tourniquette sur un polygone
Figures de Thompsen
Tourniquette : ligne brisée formée par une suite de segments deux à deux parallèles tracés sur une figure comme un polygone ou une conique.
Ces figures de Thompsen sont des problèmes intéressants de clôture : le tourniquet peut-il être infini ou se ferme-t'il ? Si oui, au bout de combien de tours ?
3.a. Tourniquette sur un triangle
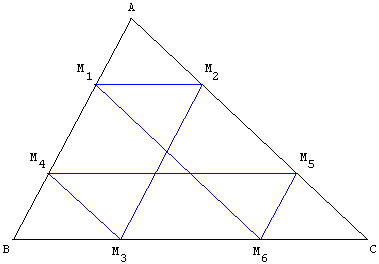
Soit ABC un triangle et M1 un point de [AB].
On effectue la construction suivante :
M2 point de [AC] tel que (M1M2) // (BC),
M3 point de [BC] tel que (M2M3) // (AB),
M4 point de [AB] tel que (M3M4) // (AC),
M5 sur [AC]…
M6 sur [BC]…
La tourniquette se referme, en général, en deux tours et M7 = M1 (en un tour si M1 est le milieu de [AB]).
![]() Télécharger la figure GéoPlan tour_tri.g2w
Télécharger la figure GéoPlan tour_tri.g2w
3.b. Tourniquette sur un quadrilatère
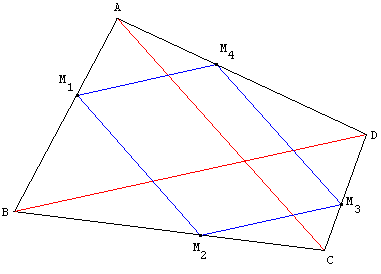
La tourniquette se referme en un tour et M5 = M1 ;
la figure M1M2M3M4 est un parallélogramme.
![]() Télécharger la figure GéoPlan tour_qua.g2w
Télécharger la figure GéoPlan tour_qua.g2w
3.c. Tourniquette sur un pentagone
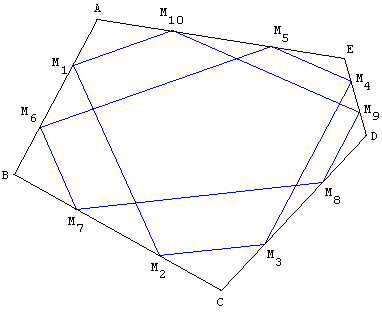
(M1M2) // (AC), (M2M3) // (BD), (M3M4) // (CE)…
La tourniquette se referme, en général, deux tours : M11 = M1 (en un tour si M1 est le milieu de [AB]).
Pour d'autres polygones, en déduire une conjecture suivant la parité du nombre de côtés.
![]() Télécharger la figure GéoPlan tour_pen.g2w
Télécharger la figure GéoPlan tour_pen.g2w
3.d. Tourniquette sur un cercle
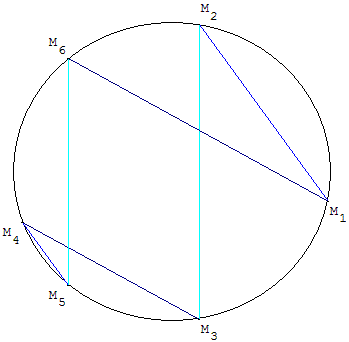
On choisit sur un cercle quatre points distincts M1, M2, M3 et M4.
On construit les deux points M5 et M6 tels que :
M5 point du cercle tel que (M4M5) // (M1M2),
M6 point du cercle tel que (M5M6) // (M2M3).
(M6M1) // (M3M4) : la tourniquette se referme et M7 = M1.
La figure M1M2M3M4M5M6 est un hexagone aux côtés deux à deux parallèles.
![]() Télécharger la figure GéoPlan tour_cer.g2w
Télécharger la figure GéoPlan tour_cer.g2w
Pour les polygones, les figures utilisent le prototype :
M2 point parallèle M1, A, C, B
qui permet de calculer le point M2, intersection de la parallèle à (AC), passant par M1, et de la droite (CB).
![]() Télécharger le prototype GéoPlan point_parallele.g2w
Télécharger le prototype GéoPlan point_parallele.g2w
Table des matières
![]() Mobile friendly
Mobile friendly
Page no 172, déplacée le 10/9/2011