Descartes et les Mathématiques

Défi : droites remarquables du triangle

Un triangle a été effacé. Il n'en reste que trois droites (médianes, hauteurs…),
retrouver le triangle à partir de ces droites remarquables !

Défi mathématique

Étant donné trois droites concourantes, construire un triangle tel que ces droites en soit les médianes, les hauteurs, les bissectrices, les médiatrices.
Lessolutions (triangles non réduits à un point) seront définis à une homothétie près (le centre étant le point de concours des trois droites). Il sera possible de déterminer arbitrairement un élément du triangle, en général, un sommet comme le point A.

Ci-dessous douze exercices de « résolution de triangle » assez difficiles de 14 à 77 ans.

Ces casse-tête géométriques consistent à retrouver un triangle à partir de points ou de droites remarquables. Ils sont particulièrement adaptés aux classes de la quatrième à la seconde. L'utilisation des logiciels Cabri-géomètre ou GéoPlan est une aide précieuse dans la recherche des solutions.

Les exercices 1 et 2 sont les plus abordables. Ils ont été réalisés en classe de quatrième en 2001, et avec guère moins de difficultés, en seconde en 2004. Les autres font l'objet du défi.

Dans un premier temps, en collège et en seconde, nous ne sommes pas posés le problème de l'existence des solutions.
Nous avons choisi trois droites non perpendiculaires, deux à deux, pour éliminer la majorité des cas particuliers et nous avons évité les angles obtus.
Déplacer les droites pour se faire une idée sur la justification des solutions.

1. Médianes

Tracer un triangle dont on connaît les trois médianes :
Trois droites données (d₁ ), (d₂ ) et (d₃ ) sont concourantes en un point G.
Construire un triangle tel que ces droites soient les médianes de ce triangle.

Une construction

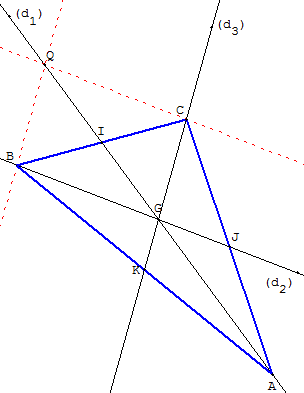
Placer arbitrairement un point A, distinct de G, sur la droite (d₁).
Tracer le point Q, symétrique de A par rapport à G.

Tracer le parallélogramme GBQC de diagonale [GQ],
ayant deux côtés sur (d₂) et (d₃) :

pour cela, la droite (d₃’), parallèle à (d₃) passant par Q, coupe (d₂) au point B,
la droite (d₂’), parallèle à (d₂) passant par Q, coupe (d₃) en C.

Le triangle ABC est une solution.

Preuve : I est le milieu [BC] et G, situé aux deux tiers à partir de A de la médiane [AI], est le centre de gravité du triangle ABC.
(GB) et (GC) sont les deux autres médianes.

Recherche : figure GéoPlan mediane2.g2w

    Télécharger la figure GéoPlan mediane3.g2w

Une autre construction

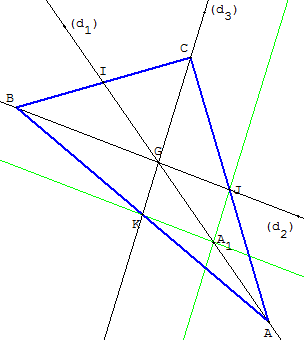
Placer le sommet A, distinct de G, sur la droite (d₁), puis le milieu A₁ de [GA] et tracer le symétrique I de A₁ par rapport à G.

Tracer le parallélogramme GJA₁K de diagonale [GA₁],
ayant deux côtés sur (d₂) et (d₃) :

Pour cela, tracer la parallèle à (d₃) qui rencontre (d₂) en J,
puis la parallèle à (d₂) qui rencontre (d₃) en K,

puis terminer les deux autres sommets B et C ; intersections respectives de (AK) et (AJ) avec (d₂) et (d₃).

La géométrie du triangle

Triangle orthopédie

Reconstituer un triangle à partir du triangle médian : le triangle, c'est le pied

2. Hauteurs

Avec trois droites concourantes, tracer un triangle dont les droites sont les hauteurs :

Tracer trois droites (d₁ ), (d₂ ) et (d₃ ) concourantes au point H et non perpendiculaires deux à deux.
Construire un triangle ABC dont les droites (d₁ ), (d₂ ) et (d₃ ) sont les hauteurs.

Construction à partir du pied d'une hauteur :
Choisir le côté [AB] en plaçant arbitrairement le pied I d'une des hauteurs, distinct de H, sur (d₃). La perpendiculaire à (d₃) passant par I coupe (d₁) en A et (d₂) en B.

Construction à partir du sommet :
Il revient même, quoi que un peu plus compliqué, de choisir un sommet A, distinct de H, sur (d₁) et de trouver le côté [AB] en traçant la perpendiculaire à (d₃) issue de A qui la coupe en I et coupe (d₂) en B.

2.a. Tracer deux autres perpendiculaires aux hauteurs

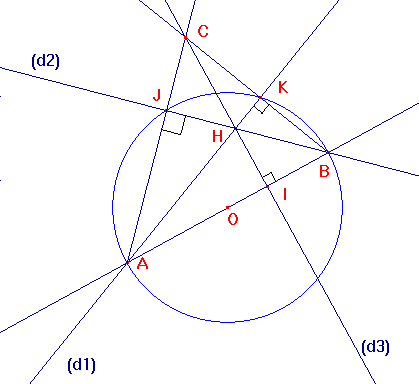
Ayant choisi le côté [AB], il reste à tracer les deux autres côtés (AJ) et (BK) du triangle ABC, perpendiculaires à (d₁) et (d₂), et à trouver le sommet C.

Pour cela, tracer le cercle de diamètre [AB] qui coupe (d₁) en K et (d₂) en J.
Les triangles AKB et AJB, inscrits dans un demi-cercle, sont rectangles. Les droites (AJ) et (BK) se coupent en C.

Le triangle ABC a pour hauteurs (d₁), (d₂) et (d₃) et est une solution de problème.

En effet, les droites (d₁) et (d₂) sont deux hauteurs du triangle ABC qui admet H comme orthocentre. (CH) est la troisième hauteur du triangle. (CH) et (d₃) sont toutes deux perpendiculaires à (AB) passant par H. Elles sont donc confondues et C est bien sur la droite (d₃).

Télécharger la figure GéoPlan hauteur4.g2w

Voir : la géométrie du triangle

Reconstituer un triangle à partir des pieds des hauteurs : le triangle, c'est le pied

2.b. Construction de deux points cocycliques sur le cercle de diamètre [AH]

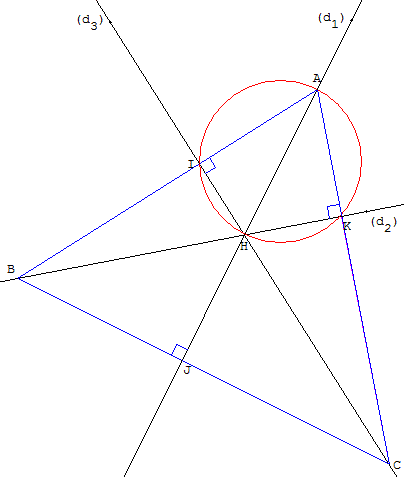
Placer un sommet quelconque A, distinct de H, sur la droite (d₁),
le cercle de diamètre [HA] coupe (d₂) et (d₃) en K et I, pieds des deux autres hauteurs.

La droite (AI) coupe (d₂) en B et (AK) coupe (d₃) en C.

Le triangle ABC est solution.

Justification

Les points I, K, B et C existent, car les droites données ne sont pas deux à deux perpendiculaires.

Télécharger la figure GéoPlan hauteur6.g2w

2.c. Construction du cercle circonscrit avec le symétrique de l'orthocentre par rapport à un côté

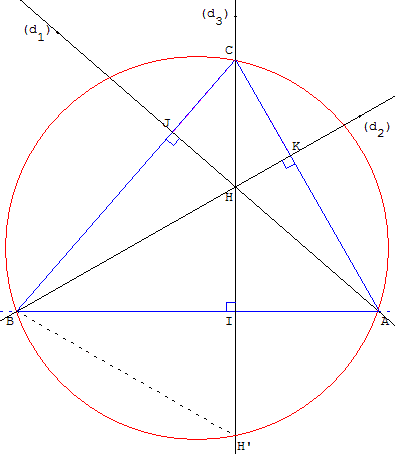
Comme pour le premier exercice, choisir le côté [AB] en plaçant arbitrairement le pied I d'une des hauteurs, distinct de H, sur (d₃). La perpendiculaire à (d₃) passant par I coupe (d₁) en A et (d₂) en B.

Le symétrique H’ de l'orthocentre, par rapport au côté (AB), se trouve sur le cercle circonscrit au triangle ABC.

Le cercle (c), circonscrit au triangle ABH’ recoupe (d₃) en C.

Le triangle ABC convient.

Preuve

Montrons que (d₂) est perpendiculaire à (AC).

Soit K le point d'intersection de (d₂) et (AC).
Étudions les triangles BIH et CKH. Leurs angles en H sont égaux comme opposés par le sommet.
Par symétrie par rapport à (BA), l'angle IBH est égal à IBH’.
Les angles ABH’ et ACH’ inscrits dans le cercle (c) sont égaux, car ils interceptent le même arc AH’

Donc IBH = HCK. Les triangles BIH et CKH ont les mêmes angles. Le triangle BIK est rectangle en I, le triangle semblable CKH est rectangle en K et CKH = 90°. (d₂) est une hauteur et H est l'orthocentre du triangle ABC. (AH) est la troisième hauteur.

Télécharger la figure GéoPlan hauteur7.g2w

3. Bissectrices

Construire un triangle connaissant ses trois bissectrices :

Tracer trois droites (d₁ ), (d₂ ) et (d₃ ) concourantes au point I et non perpendiculaires deux à deux.
Construire un triangle ABC dont les droites (d₁ ), (d₂ ) et (d₃ ) sont les bissectrices.

3.a. Changement de point de vue : problème de hauteurs

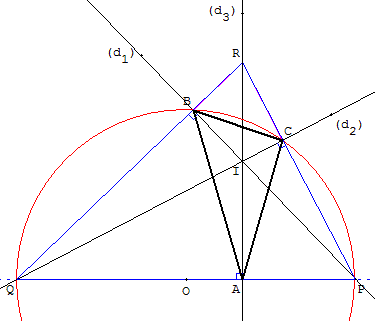
Nous ramenons au problème 2 : tracer un triangle PQR dont les droites (d₁ ), (d₂ ) et (d₃ ) sont les hauteurs.

Avec la première méthode du chapitre 2, placer un point A, distinct de I, sur la droite (d₃). La perpendiculaire à (d₃) passant par A coupe (d₁) en P et (d₂) en Q.
Pour trouver le point R, tracer le cercle de diamètre [PQ] qui coupe (d₁) en B et (d₂) en C, les triangles PBQ et PCQ, inscrits dans un demi-cercle, sont rectangles. (QB) et (PC) se coupent en R. (d₁) et (d₂) sont deux hauteurs du triangle PQR qui admet I comme orthocentre. (AI) est la troisième hauteur du triangle PQR. (AI) et (d₃) sont toutes deux perpendiculaires à (PQ) passant par I. Elles sont donc confondues et R est sur la droite (d₃).

Le triangle ABC est le triangle orthique de PQR. Les hauteurs (d₁), (d₂) et (d₃) de PQR sont les bissectrices du triangle orthique ABC. Le triangle ABC est une solution de problème.

Télécharger la figure GéoPlan bissect2.g2w

Tâche impossible

Vérifier que si deux des trois droites sont perpendiculaires, il n'est pas possible de trouver de triangle solution.

3.b. Centres de cercles exinscrits

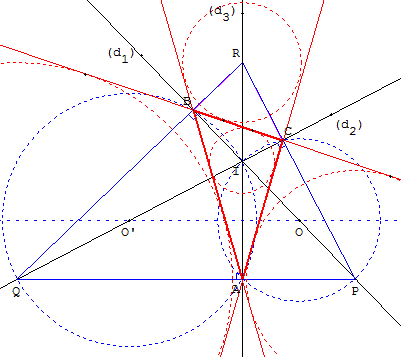
Remarque :

Dans la figure ci-contre, le point I est le centre du cercle inscrit dans le triangle ABC, P, Q et R y sont les centres des cercles exinscrits.
Les droites (PA) et (PC) sont perpendiculaires aux bissectrices (d₂) et (d₃).
Les points I, A, C et P sont cocycliques sur le cercle de diamètre [IP].

On en déduit une deuxième méthode de construction :

Placer un point quelconque A, distinct de I, sur (d₃).
La médiatrice de [IA] coupe (d₁) en O et (d₂) en O’.

Le cercle de centre O, passant par A et I, recoupe (d₂) en C (et (d₁) en P).

On construit de même le point B, intersection de (d₂) et du cercle de centre O’, passant par A et I.

Télécharger la figure GéoPlan bissect3.g2w

Retrouver cette figure : milieux des segments joignant les centres des cercles inscrit et exinscrits

3.c. Suppression d'une contrainte :

Recherche du lieu du point C lorsque B varie

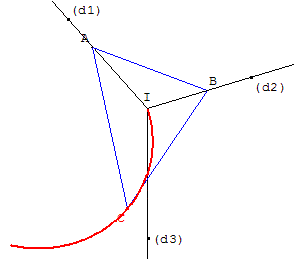
À partir de deux points A sur (d₁) et B sur (d₂) tracer le triangle ABC ayant (d₁) et (d₂) comme bissectrices.
Il suffit de tracer les droites symétriques de (AB) par rapport à (d₁) et (d₂). C est le point d'intersection de ces deux bissectrices.

En général, le point C n'est pas sur (d₃). En déplaçant le point B on peut trouver une position amenant le point C sur (d₃).

Cherchons cette position en affichant la trace du point C, il semble que le lieu soit un arc de cercle passant par I.

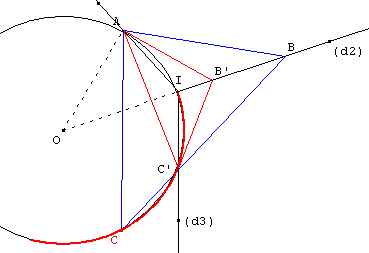
Une analyse plus précise permet de conjecturer que l'arc est contenu dans le cercle passant par A et I, dont le centre O est situé dur (d₂).

Il suffit donc de trouver le deuxième point C’ d'intersection du cercle et de (d₃) et de trouver le triangle solution AB’C’ où B’ est l'intersection de (d₂) et la droite symétrique de (AC’) par rapport à (d₁).

Télécharger la figure GéoPlan bissect_a.g2w

3.d. Cercle inscrit dans le triangle ABC

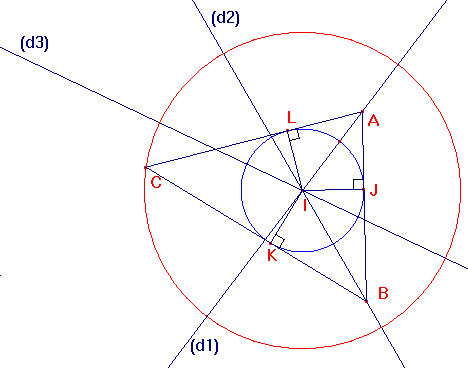
Tracer un cercle (c₁) et choisir un point J sur ce cercle. La tangente en J à ce cercle coupe, par exemple, (d₁) en A et (d₂) en B. Les deux autres tangentes au cercle, issues respectivement de A et B, tangentes en L et K, se coupent en C. Le cercle (c₁) est inscrit dans le triangle ABC.

En général, le point C n'est pas sur (d₃).
La droite (IA) est aussi la bissectrice de l'angle JÎL.
De même, la droite (IB) est la bissectrice de l'angle JÎK.
Donc, la somme des angles JÎL+JÎK est le double de l'angle AÎB.
L'angle supplémentaire KÎL est constant et lorsque J varie les triangles rectangles CIL et CIK restent constants.

Donc, le point C, situé à une distance fixe de I,
est sur un cercle (c₂) de centre I.

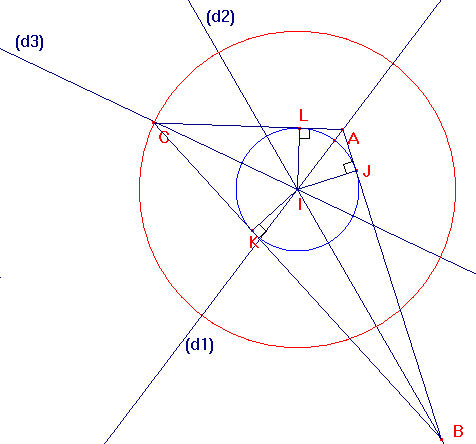
Il suffit de prendre C à l'intersection de ce cercle (c₂) et de (d₃) pour obtenir une solution de ce problème.

Télécharger la figure GéoPlan bissect6.g2w

La géométrie du triangle

Reconstituer un triangle à partir des pieds des bissectrices situés sur le cercle circonscrit : le triangle, c'est le pied

Construction à la « règle et au compas » : problèmes de construction

4. Médiatrices

Construire un triangle connaissant ses trois médiatrices :
Tracer trois droites (d₁ ), (d₂ ) et (d₃ ) concourantes au point O et non perpendiculaires deux à deux.
Construire un triangle dont les trois droites sont les médiatrices.

4.a. Changement de point de vue : problème de hauteurs

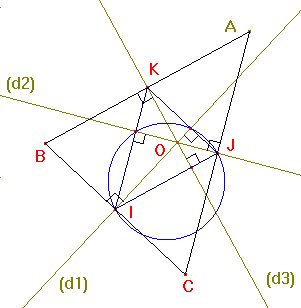
Nous ramenons au problème : construire un triangle IJK dont les droites (d₁ ), (d₂ ) et (d₃ ) sont les hauteurs.

Les médiatrices d'un triangle ABC sont les hauteurs du triangle médian IJK. Cette propriété permet ici de trouver une démonstration au niveau 4^e.

À partir d'un point I arbitraire sur (d₁), tracer comme dans l'exercice 2, le triangle IJK, ayant pour hauteurs les droites (d₁), (d₂) et (d₃).
Le triangle ABC s'obtient en traçant les parallèles aux côtés du triangle IJL, passant par les sommets opposés : la droite (AB) est la parallèle à (IJ) passant par K…

En étudiant les parallélogrammes AKIJ et KBIJ on montre que AK = IJ et IJ = BK, donc que K est le milieu de [AB], (d₃) perpendiculaires à [IJ] l'est aussi à [AB] ; c'est la médiatrice de [AB].

La deuxième propriété des milieux permet de dire que I et J sont les milieux de [BC] et de [AC] : on en déduit que les hauteurs de IJK sont les médiatrices de ABC.

Télécharger la figure GéoPlan mediat_a.g2w

4.b. Suppression d'une contrainte :

Recherche lorsque le point A varie sur un cercle de centre O

À partir de la classe de troisième.

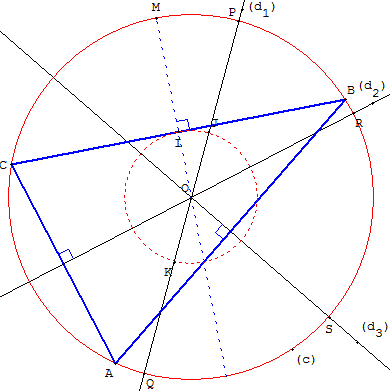
En s'affranchissant de la contrainte pour (d₁), sur un cercle fixe (c) de centre O, placer au hasard un point A puis tracer les points B et C symétriques de A par rapport respectivement à (d₃) et (d₂). Le triangle ABC est inscrit dans (c) et a pour médiatrices (d₂) et (d₃).

Soit I le milieu I de [BC]. La médiatrice (OI) de [BC] coupe le cercle (c) en un point M, situé sur la demi-droite [OI). En général, cette médiatrice est distincte de la droite (d₁) qui coupe le cercle (c) en P et Q.

En déplaçant le point A, on s'aperçoit que la longueur BC est constante.
En effet, comme angles ayant leurs côtés perpendiculaires, l'angle BÂC, égal à l'angle de droites (d₂, d₃) est constant. Soit α cet angle.
L'arc BC intercepté par cet angle est un invariant de la construction et la longueur du segment [BC] est constante.
On en déduit que l'arc moitié BM est également constant.
L'angle au centre (OC, OB) vaut 2α, l'angle au centre (OM, OB) vaut α.

Soit I le milieu I de [BC]. Comme BC est constant, IB l'est également.
Le triangle rectangle OIB, d'angle aigu α, est invariant et la longueur OI est constante.
Le milieu I est situé sur un cercle fixe (c’) de centre O.

On appelle J et K les points où la droite (d₁) coupe le cercle (c’).

Cette figure nous donne plusieurs axes pour une recherche, que nous ne justifierons pas :

Déplacer A pour que M soit sur (d₁) et observer la figure. Nous obtenons deux triangles-solutions en faisant tourner A et le triangle ABC pour que M soit en P ou soit en Q.

M en P : report d'angle

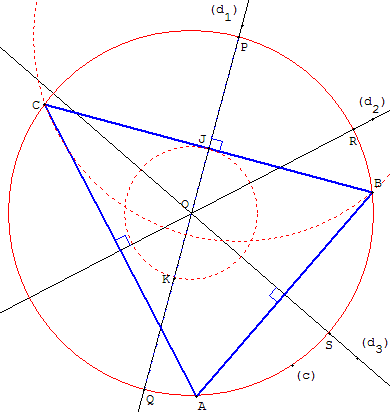
Une construction en reportant l'angle des droites (d₂, d₃) de part et d'autre de (d₁) :

La longueur MB est constante et égal à RS, où R et S sont les intersections des médiatrices (d₂) et (d₃) avec le cercle (c).

Avec le compas, reporter la longueur RS en P : le cercle de centre P et de rayon RS coupe le cercle (c) en B et C.
Le point A symétrique de C par rapport à (d₂) achève la construction du triangle ABC, solution du problème.

Justification (composition de transformations) : La rotation r de centre O, d'angle α qui transforme R en S, transforme C en P et P en B. Les points B et C sont symétriques par rapport à (d₁).
B est l'image de C dans la rotation de centre O, d'angle 2α. Cette rotation est la composé s₃ o s₂ de la symétrie axiale par rapport à (d₂), suivie de la symétrie par rapport à (d₃) :
B = s₃ o s₂ (C).
Par construction A symétrique de C par rapport à (d₂) s'écrit C = s₂ (A).
En composant B = s₃ o s₂ (s₂ (A)) = s₃ (A) car s₂o s₂ est l'identité. B est symétrique de A par rapport à (d₃). (d₃) est bien la troisième médiatrice du triangle ABC.

Pied d'une médiatrice

Une autre construction en traçant la tangente en J à (c’). Cette tangente coupe le cercle (c) en B et C.
Le point A, symétrique de C, termine la construction d'une solution.

Justification : l'angle au centre (OC, OB) est le double de l'angle inscrit (AC, AB) égal à α.
(d₁) est la médiatrice de [CB] et la rotation de centre O, d'angle 2α, transforme C en B. On se retrouve dans les conditions de la justification précédente.

M en Q : report d'angle

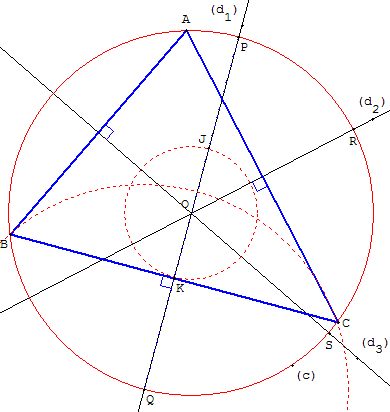
Le cercle de centre Q et de rayon RS coupe le cercle (c) en B et C.
Terminer avec le point A symétrique de B par rapport à (d₃).

Pied d'une médiatrice

Une dernière construction en traçant la tangente en K à (c’). Cette tangente coupe le cercle (c) en B et C.

Télécharger la figure GéoPlan mediat_b.g2w

La géométrie du triangle

4.c. Recherche

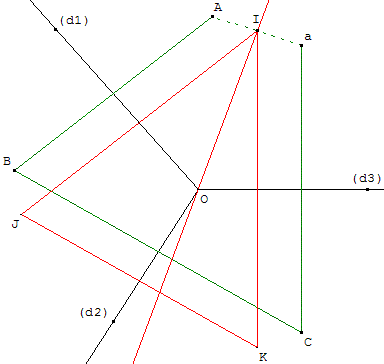
Si nous essayons de déterminer A, B étant son symétrique par rapport à (d₁) et C le symétrique de B par rapport à (d₂), je devrais retrouver A en symétrisant par rapport à (d₃), donc au terme de trois symétries successives d'axes concourants en O.
Un enseignant sait que la composée de trois symétries est une symétrie. O étant un point fixe, l'axe (d) passe aussi par O.
Dès lors, il faut et il suffit que le point A soit pris sur d.

À une homothétie de centre O près, si une solution il y a, elle est unique.

À partir d'un point A variable dans le plan traçons les symétriques B et C.

Soit a le symétrique de C par rapport à (d₃). Si a = A on a une solution, en général, ce n'est pas le cas et soit I le milieu [aA] et (d) = (OI) la médiatrice de [aA].

Le point I ou tout point de (d) permet de trouver une solution IJK.

Télécharger la figure GéoPlan mediat_c.g2w

4.d. Méthode avec une translation

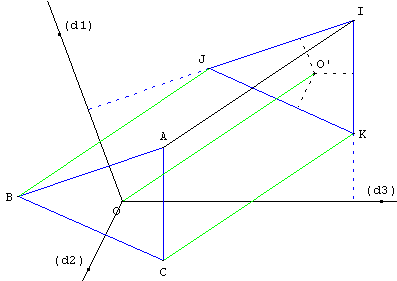
À partir d'un point I, tracer les perpendiculaires à (d₁) et (d₂), J étant un point d'une des perpendiculaires, la perpendiculaire à (d₃) passant par J coupe la deuxième perpendiculaire en K.

Le triangle IJK a ses médiatrices parallèles à (d₁), (d₂) et (d₃). Soit O’ leur point de concours.

Il suffit alors de la translation amenant O’ sur O pour obtenir un triangle ABC solution.

Télécharger la figure GéoPlan mediat_d.g2w