Descartes et les Mathématiques
Droites remarquables du triangle (ménéliennes)
Droite de Simson (ou droite de Wallace) - Droite de Steiner.
Sommaire
Dans un triangle, une cévienne est une droite issue d'un sommet (les hauteurs, médianes, bissectrices sont des céviennes).
Voir : Droites remarquables du triangle (Céviennes)
Droites du triangle autres que des céviennes
Ménélienne
Dans un triangle, une ménélienne est une droite (transversale) ne passant pas par un des sommets.
1. Droite de Simson (ou droite de Wallace)
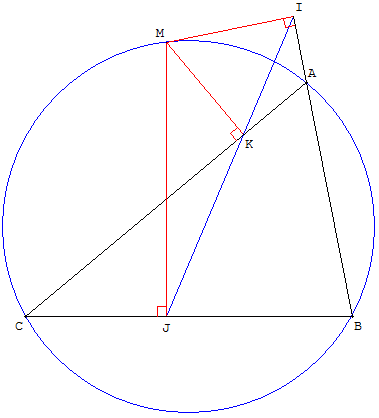
Dans un triangle ABC (non plat), soit M un point du plan et I, J et K les projetés orthogonaux de M sur les droites (AB), (BC) et (AC).
Le point M est sur le cercle circonscrit au triangle si et seulement si I, J et K sont alignés.
Dans ce cas, la droite portant les points I, J et K s'appelle la droite de Simson associée au point M.
Cette droite est aussi qualifiée de droite de Wallace du point M.
Théorème : pour que quatre points soient cocycliques, il faut et il suffit que les projections orthogonales de l'un d'eux sur les côtés du triangle déterminé par les trois autres soient trois points alignés.
Théorème de Steiner : « L'enveloppe des droites de Simson d'un triangle est une deltoïde. »
Télécharger la figure GéoPlan simson.g2w
2. Droite de Steiner
Jakob Steiner - géomètre suisse (1796-1863)
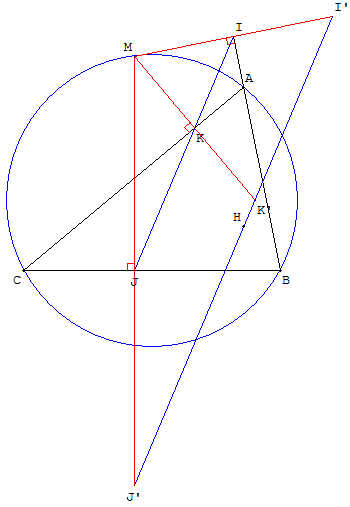
Dans un triangle ABC (non plat), soit M un point du plan et I’, J’ et K’ les symétriques de M par rapport aux droites (AB), (BC) et (AC). Alors M est sur le cercle circonscrit au triangle si et seulement si les points I’, J’ et K’ sont alignés.
Dans ce cas, la droite portant les points I’, J’ et K’ s'appelle la droite de Steiner associée au point M.
L'orthocentre H du triangle est situé sur la droite de Steiner.
Une homothétie de centre M et de rapport 2 transforme la droite de Simson en droite de Steiner.
Télécharger la figure GéoPlan steiner.g2w
Publimath : droite de Steiner
Théorème de Steiner−Lehman
Si deux bissectrices d'un triangle ont même longueur, le triangle est isocèle.
Puissance d'un point
La puissance d'un point par rapport à un cercle a été introduite par Jakob Steiner en 1830.
3. Droite de Van Aubel
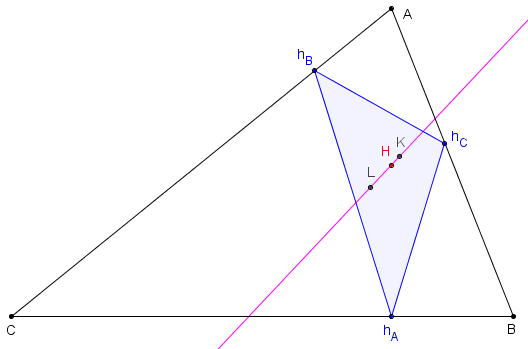
Dans un triangle ABC, d'orthocentre H, hAhBhC est le triangle orthique.
La droite de van Aubel (LH) joint le point de Lemoine à l'orthocentre du triangle.
Cette droite contient le point de Lemoine K du trianle orthique.
K est le point X(53) du triangle de référence
Avec GeoGebra : TriangleCentre[A, B, C, 53].
Figure interactive dans GeoGebraTube : droite de Van Aubel
Voir aussi : configuration de Van Aubel − Quatre triangles autour d'un quadrilatère
Table des matières
Dans d'autres pages du site
Index triangles
Google friendly
Page no 141, créée le 11/5/2009
mise à jour le 3/6/2016