Descartes et les Mathématiques

Triangle orthique

Triangle et axe orthiques - Cercle de Taylor.

1. Triangle orthique

de : Höhenfußpunktdreieck

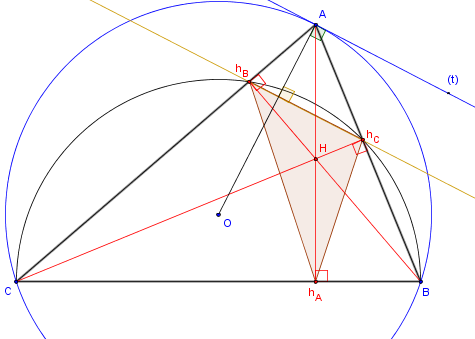
Le triangle orthique d'un triangle a pour sommets les pieds des hauteurs de ce triangle.

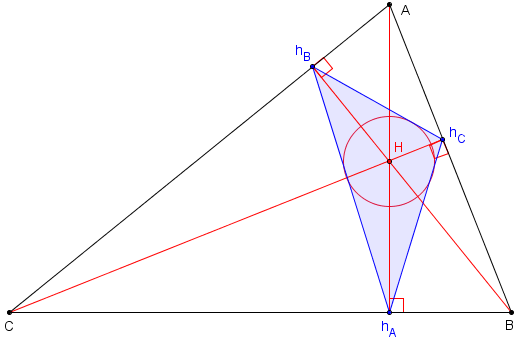
Dans un triangle ABC acutangle (non rectangle dont les trois angles sont aigus),
les hauteurs (Ah_A), (Bh_B) et (Ch_C), concourantes en son orthocentre H,
sont les bissectrices (h_AH), (h_BH) et (h_CH) du triangle orthique h_Ah_Bh_C.

Les hauteurs du triangle initial sont les bissectrices du triangle orthique :
l'orthocentre du triangle initial est le centre du cercle inscrit dans le triangle orthique.

Figure interactive dans GeoGebraTube : triangle orthique

Construction au compas seul

Ci-dessous deux constructions au compas avec des cercles définis par leurs diamètre ou définis par des points cocycliques.

Nous avons déjà rencontré ces figures dans le chapitre hauteur de la géométrie du triangle ou avec le théorème de Clifford.

Triangle de lumière

« Le triangle orthique est l'unique trajectoire de billard triangulaire qui se ferme ».

Triangle de lumière : si les côtés du triangle sont des miroirs, un rayon lumineux porté par un côté du triangle orthique
sera identique à lui-même après trois réflexion par les miroirs.

Voir aussi : rectangle de lumière

Problème de Fagnano (mathématicien italien 1682-1766) : triangle de périmètre minimum

Trouver le triangle, inscrit dans un triangle, qui a le plus petit périmètre.

Le triangle de périmètre minimal dont les sommets appartiennent aux côtés d'un triangle initial est le triangle orthique
Voir : géométrie en troisième.

Article exporté dans WikiPédia : triangle orthique

1.b. Les hauteurs sont les bissectrices du triangle orthique

Démonstration avec trois cercles ayant pour diamètre les côtés du triangle

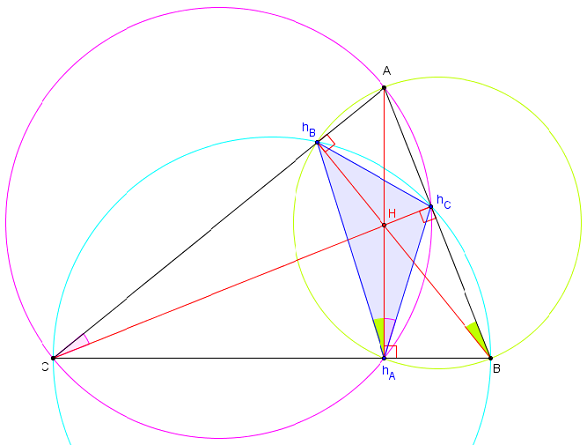
Dans un triangle ABC acutangle (triangle non rectangle dont les trois angles sont aigus),
les hauteurs (Ah_A), (Bh_B) et (Ch_C), concourantes en son orthocentre H,
sont les bissectrices (h_AH), (h_BH) et (h_CH) du triangle orthique h_Ah_Bh_C.

Cette propriété peut être utilisée pour montrer que les hauteurs d'un triangle sont concourantes.

Les points B, A, h_B, h_A sont cocycliques sur le cercle de diamètre [AB].
On a les égalités d'angles inscrits : (h_Ah_B, h_AA) = (Bh_B, BA).

A, C, h_A, h_C sont cocycliques sur le cercle de diamètre [BC],
d'où (Bh_B, Bh_C) = (Ch_B, Ch_C), soit (Bh_B, BA) = (CA, Ch_C).

A, C, h_A, h_C sont cocycliques sur le cercle de diamètre [AC],
d'où (CA, Ch_C) = (h_AA, h_Ah_C).
Par transitivité : (h_Ah_B, h_AA) = (Bh_B, BA) = (CA, Ch_C) = (h_AA, h_Ah_C),
soit (h_Ah_B, h_AA) = (h_AA, h_Ah_C) et la droite (Ah_A) est une bissectrice de (h_Ah_B, h_Ah_C).

Remarque : dans un triangle obtusangle en A, (Ah_A) est la bissectrice extérieure de (h_Ah_B, h_Ah_C).

Figure interactive dans GeoGebraTube : trois cercles pour les bissectrices du triangle orthique

1.c. Démonstration avec deux cercles passant par l'orthocentre

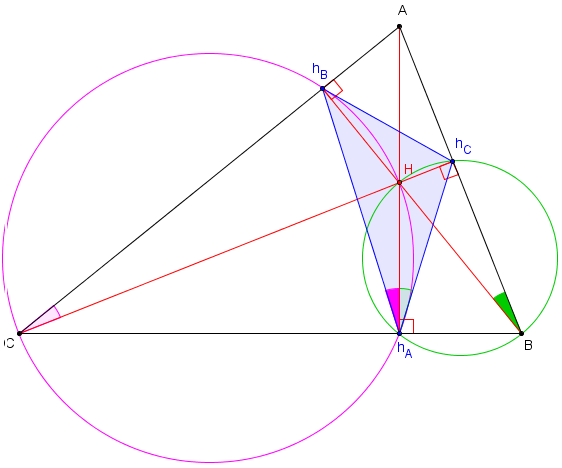
Classe de troisième

Pour vérifier que les hauteurs du triangle ABC sont les bissectrices de h_Ah_Bh_C,
étudier en particulier la bissectrice de h_BÂ’h_C.

Pour cela, tracer les cercles de diamètres [BH] et [CH],
montrer l'égalité des angles inscrits :
h_Ch_AH = h_CBH et Hh_Ah_B = HCh_B
et conclure que (h_AH) est la bissectrice de h_Bh_Ah_C en remarquant que les angles h_CBH et HCh_B,
ayant des côtés perpendiculaires, sont égaux.

Figure interactive dans GeoGebraTube : les hauteurs sont les bissectrices du triangle orthique

Classe de première L

Construction d'un triangle connaissant le pied des trois hauteurs.

Les hauteurs sont les bissectrices du triangle dont les sommets sont les pieds des hauteurs.

Voir : le triangle, c'est le pied

2. Perpendiculaires et parallèles aux côtés du triangle orthique

Soit (c) le cercle circonscrit au triangle ABC de centre O et (t) la tangente en A à ce cercle.
(c₁) est le cercle de diamètre [BC].
Les points h_B et h_C sont situés sur ce cercle.

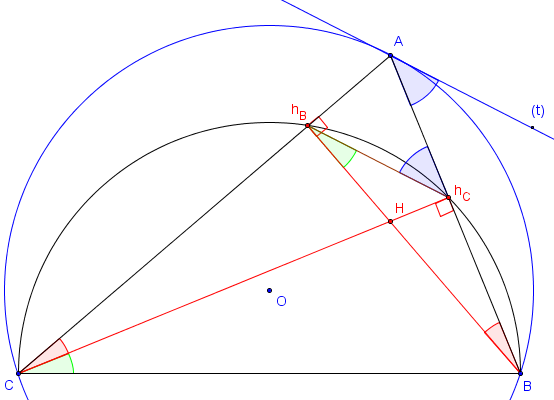
Une étude des angles inscrits permet de montrer que (h_Bh_C) est parallèle à (t) ; en effet :

L'angle ACB inscrit dans le cercle circonscrit (c) est égal à l'angle BÂt de la corde et de la tangente.

L'angle extérieur h_Bh_CA du triangle Bh_Bh_C est égal à la somme des deux angles intérieurs :
h_Bh_CA = h_Ch_BB + h_BBh_C.

Des égalités des angles inscrits dans (c₁) :
h_BCh_C = h_BBh_C pour l'arc  h_Bh_C
et h_CCB = h_Ch_BB pour l'arc  h_CB;

on déduit que :
ACB = h_BCh_C + h_CCB = h_BBh_C + h_Ch_BB = h_Bh_CA.
Les angles alternes-internes h_Bh_CA  et BÂt sont égaux (égaux à ACB).
Le côté du triangle orthique (h_Bh_C) est parallèle à la tangente (t).

Voir ci-dessous :
« Les tangentes au cercle circonscrit passant par les sommets du triangle sont parallèles aux côtés du triangle orthique ».

Figure interactive dans GeoGebraTube : Parallèle à un côté du triangle orthique (démonstration)

3. Cotés des triangles antiparallèles

3.a. Un côté du triangle orthique et le côté opposé du triangle sont antiparallèles aux deux autres côtés du triangle

Soit ABC un triangle, non rectangle ; O le centre de son cercle circonscrit (c) ; H l'orthocentre et h_A, h_B, h_C les pieds des hauteurs issues de A, B, C.

(h_Bh_C) est parallèle à (t),
donc (OA) , rayon du cercle circonscrit perpendiculaire à la tangente, est perpendiculaire à (h_Bh_C).

Les côtés du triangle orthique sont perpendiculaires aux rayons du cercle circonscrit issus des sommets.

En raison des angles droits formés par les hauteurs Bh_B et Ch_C,
les triangles rectangles Bh_BC et Bh_CC sont inscrits dans le cercle (c₁) de diamètre [BC].

Les points B, C, h_B, h_C sont cocycliques, donc (h_Bh_C) est antiparallèle à (BC) par rapport à (h_CB, h_BC),
soit par rapport à (AB, AC).

3.b. Deux côtés du triangle, concourants, en un sommet, sont antiparallèles avec la hauteur
et le rayon du cercle circonscrit issus de ce sommet :

En effet, d ans le triangle rectangle ACh_A, rectangle en h_A :
(AC, Ah_A) + (CB, CA) = .
La corde (At) est perpendiculaire au rayon [OA] :
(AO, AB) + (AB, At) = .

L'angle (CB, CA) inscrit dans le cercle circonscrit (c) est égal à l'angle (AB, At) de la corde AB et de la tangente At.

Par soustraction des deux premières égalités, on trouve :
(AC, Ah_A) – (AO, AB) = 0, soit (AC, AH) = (AO, AB).

(AB, AC) est antiparallèle à (AH, AO).

Les droites (BC, At) sont perpendiculaires à (AH, AO), donc (BC, At) est antiparallèle à (AB, AC).

Figure interactive dans GeoGebraTube : parallèle à un côté du triangle orthique

3.c Théorème de Nagel

Deux côtés du triangle, concourants en un sommet, sont isogonaux avec la hauteur et le rayon du cercle circonscrit issus de ce sommet.

On a démontré ci-dessus qu'à partir du sommet A, les paires de droites (AB, AC) et (AH, AO) sont isogonales.
On peut démontrer de même qu'à partir du sommet B, les paires de droites (BA, BC) et (BH, BO) sont aussi isogonales.

Leurs deux points d'intersection sont conjugués,
d'où le théorème de Nagel :

le centre du cercle circonscrit est le conjugué isogonal de l'orthocentre.

Autre démonstration

Le cercle d'Euler est le cercle podaire des points O ou H par rapport au triangle ABC.

Les points O et H, symétriques par rapport au centre Ω du cercle d'Euler, sont isogonaux.

3.d. Conséquence : tangentes au cercle circonscrit

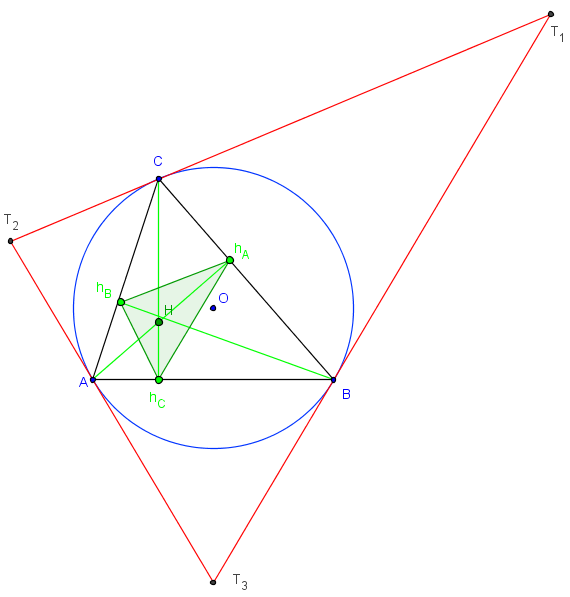
La tangente en A au cercle circonscrit est antiparallèle à (BC) par rapport à (AB, AC).

(h_Bh_C) est antiparallèle à (BC), donc le rayon (OA) est perpendiculaire à (h_Bh_C) et (AT₂) // (h_Bh_C).

Les côtés du triangle tangentiel sont parallèles à ceux du triangle orthique

Les tangentes au cercle circonscrit, passant par les sommets du triangle, forment le triangle tangentiel, ses côtés sont parallèles aux côtés du triangle orthique.

Figure interactive dans GeoGebraTube : triangle tangentiel

4.a Axe orthique

Le cercle d'Euler est le cercle circonscrit au triangle orthique.

L'axe orthique d'un triangle est l'axe radical du cercle circonscrit au triangle et du cercle d'Euler de ce triangle.

L'axe orthique d'un triangle est la droite passant par les trois points d'intersection des côtés du triangle et de ceux de son triangle orthique.

Il est perpendiculaire à la droite d'Euler (OH).

Alignement des trois points d'intersection des côtés d'un triangle avec ceux de son triangle orthique.

Dans un triangle ABC (ni rectangle, ni isocèle), soit h_A(respectivement h_B et h_C) le pied de la hauteur issue de A (respectivement issue de B et de C).

On note o_A l'intersection de (BC) et de (h_Bh_C),
 o_B l'intersection de (AC) et de (h_Ah_C)
 o_C l'intersection de (AB) et de (h_Ah_B).

Les trois points o_A, o_B et o_C sont alignés sur une droite nommée axe orthique du triangle.

Indications

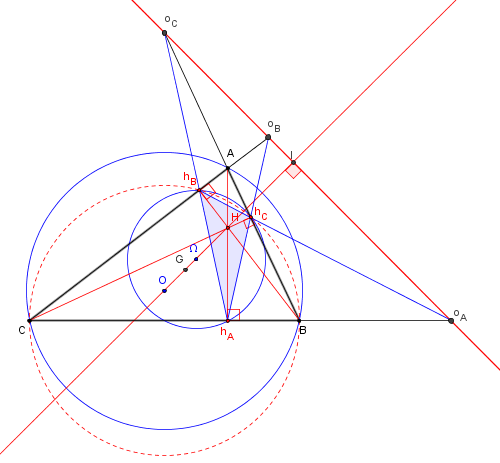
Les points h_B et h_C sont situés sur le cercle de diamètre [BC].
La puissance de o_A par rapport à ce cercle est :

o_AB × o_AC = o_Ah_B × o_Ah_C.

o_AB × o_AC est la puissance o_A par rapport au cercle (c) circonscrit à ABC.
o_Ah_B × o_Ah_C est la puissance o_A par rapport au cercle d'Euler (c_E) circonscrit à h_Ah_Bh_C.

Le point o_A a donc même puissance par rapport à (c) et (c_E), o_A est situé sur leur axe radical.

On montre de même que les deux autres points d'intersection o_B et o_C ont même puissance par rapport à (c) et (c_E).

Les points o_A, o_B et o_C sont situés sur une même droite, axe radical de (c) et (c_E) ; cet axe est appelé axe orthique du triangle.

Figure interactive dans GeoGebraTube : axe orthique

Voir : Vingt quatre points sur l'axe orthique

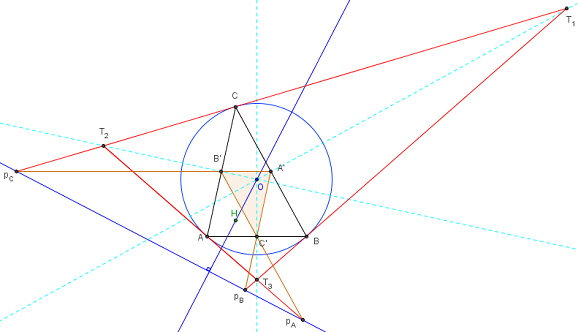
4.b. Perspective des triangles médian et tangentiel

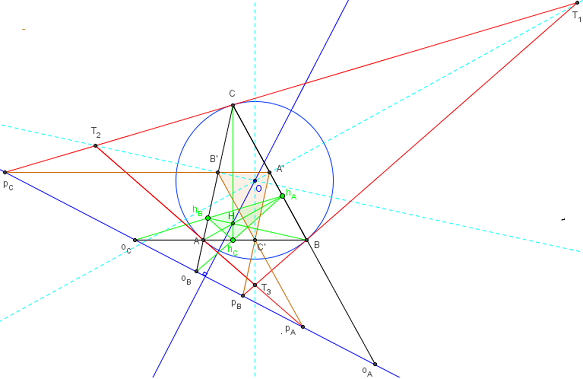
Les triangles médian A’B’C’ et tangentiel T₁T₂T₃ d'un triangle ABC sont en perspective de pôle O, le centre du cercle circonscrit de ABC.

La forme forte du théorème de Desargues montre l'alignement des points de concours p_A, p_B et p_C sur l'axe de la perspective (ou axe d'homologie).

en : archaically perspectrix

Cet axe est l'axe orthique du triangle de référence.

Figure interactive dans GeoGebraTube : Perspective des triangles médian et tangentiel

5.a. Médiatrice d'un côté du triangle orthique

Dans un triangle ABC, A’, B’ et C’ sont les milieux des côtés,
h_Ah_Bh_C est le triangle orthique.
I est le milieu de [h_Bh_C].

  – Montrer que A’ est un point de la médiatrice de [h_Bh_C].

Indication

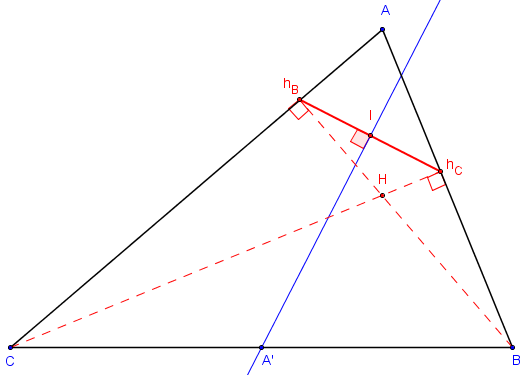
  • Montrer que les points B, h_B, h_C et C sont sur un même cercle dont on précisera le centre et le rayon.
  • Montrer que le point A’ appartient à la médiatrice de [h_Bh_C].
  • En déduire que la droite (A’I) est la médiatrice de [h_Bh_C].

5. b Justification

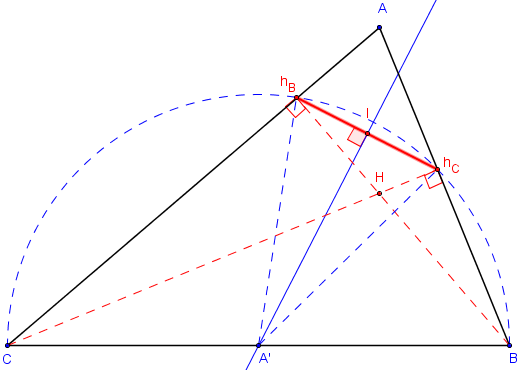
Comme les angles Bh_BC et Bh_CC sont droits, h_B et h_C sont deux points du demi-cercle de diamètre [BC].

Les longueurs A’h_B et A’h_C, médianes des triangles rectangles Bh_BC et Bh_CC, sont égales au rayon BC de ce cercle.

Le point A’, équidistant de h_B et h_C, est un point de la médiatrice de [h_Bh_C].

Les médiatrices du triangle orthique passent par les milieux des côtés du triangle

Figure interactive dans GeoGebraTube : médiatrice d'un côté du triangle orthique

5.c. Centre du cercle d'Euler

Les triangles rectangles Bh_BC et Bh_CC sont inscrits dans le cercle de diamètre [BC] de centre A’.

[h_Bh_C] est une corde de ce cercle, sa médiatrice passe par le milieu A’ de [BC].

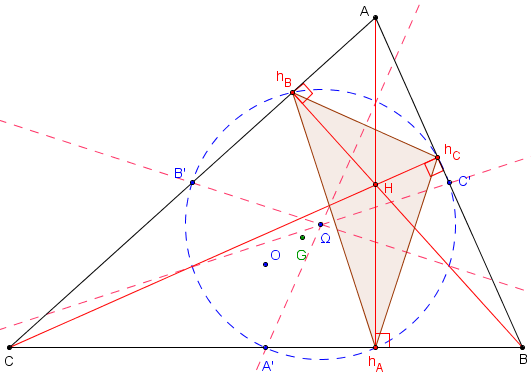
Remarque : Le centre Ω du cercle d'Euler (c_E) circonscrit au triangle orthique h_Ah_Bh_C est aussi situé sur cette médiatrice.

Les médiatrices du triangle orthique passent par les milieux des côtés du triangle ABC.

Ω, centre du cercle d'Euler, est le milieu de [OH].

Figure interactive dans GeoGebraTube : cercle d'Euler circonscrit au triangle orthique

6. Triangle médian du triangle orthique

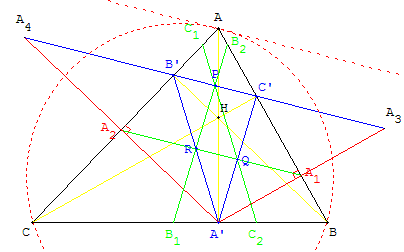
Soit un triangle ABC non rectangle,
soit A’, B’ et C’ les pieds des hauteurs du triangle ABC issues respectivement de A, B et de C,
on note A₁ et A₂ les projections orthogonales de A’ sur (AB) et (AC),
A₃ et A₄ les symétriques de A’ par rapport à A₁ et A₂.

La droite (A₃A₄) est parallèle à (A₁A₂),
les points B’, C’, A₃ et A₄ sont alignés,
la droite (A₁A₂) contient les milieux Q et R des côtés [A’C’] et [A’B’] du triangle orthique du triangle ABC,
(A₁A₂) est un des côtés de PQR, triangle médian du triangle orthique.

A₃A₄ est égal au périmètre du triangle orthique A’B’C’.
Ce périmètre est égal à 8S²/(abc) où S est l'aire du triangle ABC et où a, b, c sont égaux aux longueurs des côtés du triangle ABC.

Télécharger la figure GéoPlan t_orthi4.g2w

Figure exportée dans WikiPédia :triangle orthique

7. Cercle de Taylor

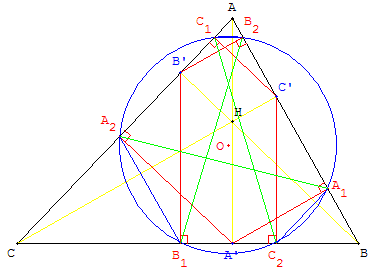
Les projections des pieds des hauteurs sur les deux autres côtés d'un triangle
forment six points situés sur un même cercle, appelé cercle de Taylor (mathématicien anglais 1685-1731).

Soit un triangle ABC non rectangle,
soit A’, B’ et C’ les pieds des hauteurs du triangle ABC issues respectivement de A, B et de C,
on note A₁ et A₂ les projections orthogonales de A’ sur (AB) et (AC),
B₁ et B₂ les projections orthogonales de B’, C₁ et C₂ les projections orthogonales de C’.

On a :
(A₁A₂, BC) = (AB, AC), la droite (A₁A₂) est antiparallèle de (BC) par rapport à (AB) et (AC),
et des propriétés analogues pour (B₁B₂) et (C₁C₂).

(B₂C₁) est parallèle à (BC). De même (A₁C₂) //(AC) et (A₂B₁)//(AB).

On trouve la configuration d'un cercle de Tücker particulier, dit cercle de Taylor.
On retrouve A₁A₂ = B₁B₂ = C₁C₂.

L'hexagone ayant pour sommets ces six projections est l'hexagone de Catalan (mathématicien belge, 1814-1894).

Les côtés opposés de l'hexagone de Catalan A₁B₂C₁A₂B₁C₂ sont parallèles, deux à deux,
et les diagonales [A₁A₂], [B₁B₂], [C₁C₂] sont de même longueur.

Télécharger la figure GéoPlan c_taylor.g2w

WikiPédia ja : 六点円

8. Centre du cercle de Taylor

Centre du cercle inscrit dans le triangle médian du triangle orthique

Les trois droites (A₁A₂), (B₁B₂) et (C₁C₂) joignant ces projections sont parallèles aux côtés du triangle orthique
et coupent ces côtés en leurs milieux P, Q et R. Ces droites déterminent les côtés du triangle PQR
qui est le triangle médian du triangle orthique.

Le centre du cercle de Taylor est le centre du cercle inscrit dans le triangle médian du triangle orthique lorsque le triangle est acutangle.

Démonstration

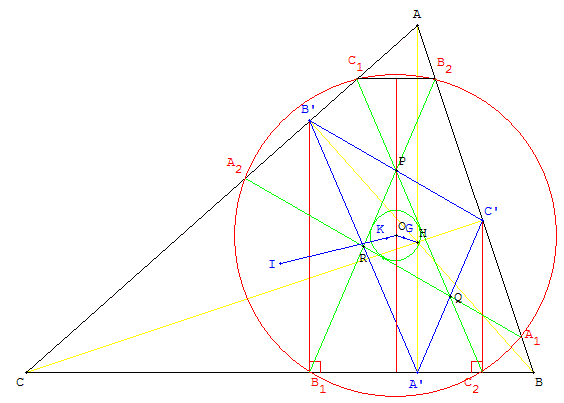
Les points B₁ et C₂ sont situés sur le cercle de Taylor, la médiatrice (d) de [B₁C₂] contient le centre O du cercle.

Les droites (B₁B’), (d) et (C₂C’) étant trois parallèles équidistantes,
d'après le théorème de Thalès, la droite (d) coupe [B’C’] en son milieu P.

D'après les propriétés du triangle médian du triangle orthique,
le point P est à l'intersection des droites (B₁B₂) et (C₁C₂). Le triangle B₁PC₂ est isocèle.
(d) médiatrice de [B₁C₂] est aussi une des bissectrices de l'angle PRQ.

Le point O est situé sur une bissectrice de l'angle PRQ.
On montre, de même, que O est situé sur les bissectrices de RPQ et de RQP.

Le point O est situé à l'intersection de trois bissectrices de PQR.
Si le triangle ABC est acutangle, les trois bissectrices sont intérieures
et O est le centre du cercle inscrit dans le triangle médian du triangle orthique.

Télécharger la figure GéoPlan c_taylor_centre.g2w

Cas particulier : triangle obtusangle

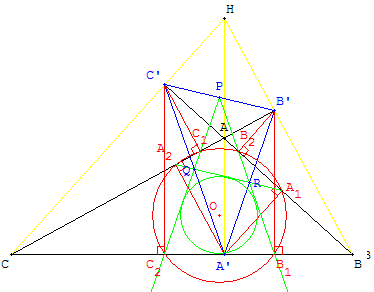
le centre est celui du cercle exinscrit dans l'angle de sommet P, milieu de [B’C’]
(respectivement Q milieu de [C’A’], R milieu de [A’B’]) si A (respectivement B, C) est obtus.

Télécharger la figure GéoPlan c_taylor_obtus.g2w

Intersection de droites

Soit I le centre du cercle circonscrit à ABC et K le point de Lemoine ;
le centre O du cercle de Taylor est l'intersection de (IK) et de la droite (HG)
joignant l'orthocentre H du triangle ABC avec le centre de gravité G du triangle orthique A’B’C’.

Indications

Un cercle de Taylor est un cercle de Tücker, son centre est situé sur la droite (IK).

L'homothétie de centre G et de rapport − transforme le triangle orthique A’B’C’ en PQR, triangle médian du triangle orthique.
H centre du cercle inscrit ou exinscrit dans A’B’C’ est transformé en O centre du cercle inscrit ou exinscrit dans PQR.
= − , O, G et H sont alignés. O est situé sur la droite (HG).

Quadrature n^o 63 Janvier-Mars 2007

Table des matières

Dans d'autres pages du site

Index triangles

Droites remarquables du triangle

Cercles remarquables du triangle

Google friendly