Descartes et les Mathématiques
Le rectangle au collège avec la géométrie dynamique
Comment tracer un rectangle à la règle et au compas,
Sommaire
1. Dessiner un rectangle
2. Le rectangle dans la planche à clous avec GeoGebra
3. Dessiner un rectangle de longueur 5, de largeur 3
5. Balade sur l'hypoténuse avec GéoPlan
7. Quadrilatère dans un rectangle : napperon
1. Construire un rectangle
Comment faire un rectangle avec GéoPlan
Dessiner le segment [AB], tracer la perpendiculaire à [AB] passant par A,
placer un point D sur cette perpendiculaire,
tracer les parallèles à (AB) passant par C et à (BC) passant par A,
C est le point d'intersection de ces deux parallèles.
Tracer les segments [BC], [CD] et [AD].
Il est possible de tracer les diagonales et le cercle circonscrit au rectangle.
Comment calculer la longueur d'une diagonale d'un rectangle
Les deux diagonales sont de même longueur et se coupent en leur milieu :
Pour la diagonale [AC], étudier un des triangles rectangles ABC ou ADC, et y calculer AC avec le théorème de Pythagore :
AC2 = AB2 + BC2 = L2 + l2 pour un rectangle de longueur AB = L et de largeur BC = l.
Aire d'un rectangle
L'aire du rectangle de longueur L et de largeur l est égale au produit Ll.
De tous les rectangles de périmètre donné, celui qui a l'aire maximum est le carré.
2.Le rectangle dans la planche à clous avec GeoGebra
Géoplan 3 × 3
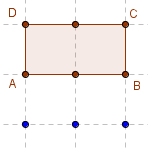
Aire(ABCD) = 2.
longueur × largeur = AB × AD = 2.
Figure interactive dans GeoGebraTube : rectangle dans le géoplan 3 × 3
Géoplan 5 × 5
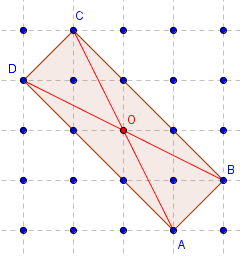
Aire(ABCD) = 6.
Les diagonales sont de même longueur 2
.
Figure interactive dans GeoGebraTube : rectangle dans le géoplan 5 × 5
3. Construire un rectangle de longueur 5 et de largeur 3
Comment construire un rectangle avec règle et compas
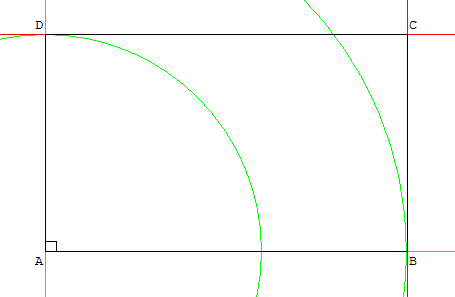
Placer un point A, dessiner une demi-droite d'origine A et un cercle de centre A et de rayon la longueur 5 ;
le point B est à leur intersection, tracer le segment [AB].
Tracer la perpendiculaire à [AB] passant par A et un cercle de centre A et de rayon la larguer 3 ;
placer le point D sur cette perpendiculaire, à une des intersections avec le cercle, dessiner le segment [AD].
Tracer les parallèles à (AB) passant par C et à (BC) passant par A ;
Le quatrième sommet C est le point d'intersection de ces deux parallèles ;
tracer les segments [BC] et [CD].
Télécharger la figure GéoPlan dessiner_rectangle.g2w
4. Comparer deux longueurs
Définitions et propriétés
• Les définitions et les propriétés contribuent à développer la connaissance des objets et leur intérêt pour représenter les situations. Elles constituent d'autre part, dans le cadre de la géométrie, les références nécessaires sur lesquelles peut se faire l'apprentissage du raisonnement déductif.
Ainsi, l'exemple suivant, dans lequel les justifications sont simples et accessibles aux élèves, permet de réinvestir d'une façon non triviale le fait que les diagonales d'un rectangle sont de même longueur (et que tous les rayons d'un même cercle sont de même longueur).
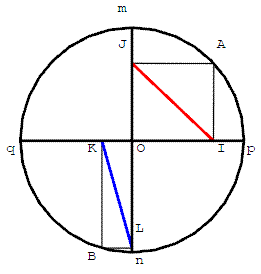
La figure ci-contre représente un cercle de centre O et deux de ses diamètres perpendiculaires.
OIAJ et OKBL sont deux rectangles.
Comparer les longueurs des segments [IJ] et [KL] ?
L'étude ne vise pas un simple traitement instrumenté, mais concerne une configuration sur laquelle fonctionnent des propriétés. Il ne s'agit plus de modélisation pour résoudre un problème concret, mais d'une situation purement abstraite, représentative d'une autre famille de problèmes de géométrie, relative à l'utilisation directe (sans changement de cadre) d'un corpus de définitions et de propriétés pour établir une preuve.
Ressources pour les classes de 6e, 5e, 4e et 3e - Géométrie au collège
Projet de document d'accompagnement mathématique - Juillet 2007
Avec la géométrie dynamique
Classe de sixième
La figure représente un cercle de centre O, [MN] et [PQ] sont deux de ses diamètres perpendiculaires.
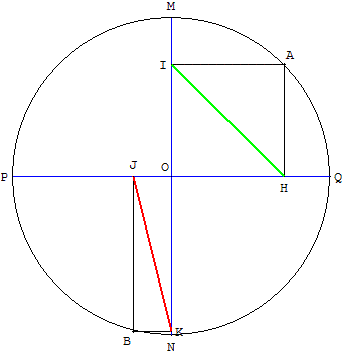
OHAI et OJBK sont deux rectangles.
Que peut-on dire des longueurs des deux segments [HI] et [JK] ?
Indications
Les justifications sont simples et accessibles aux élèves, et permettent de réinvestir, d'une façon non triviale, le fait que les diagonales d'un rectangle sont de même longueur et que tous les rayons d'un même cercle sont de même longueur.
Télécharger la figure GéoPlan comparer_longueur.g2w
Voir L@ feuille à problèmes : Transformations d'un problème
5. Balade sur l'hypoténuse
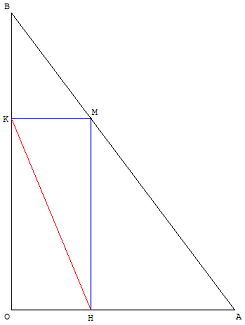
Recherche de minimum : comment caractériser le point solution ?
Il s'agit d'étudier le problème suivant :
Dans un triangle ABC rectangle en C, M est un point de l'hypoténuse, H et K sont sur les côtés de l'angle droit, tels que HMKC soit un rectangle.
Pour quelle position du point M la longueur du segment [HK] est-elle la plus petite possible ?
Variante : rectangle dans un triangle rectangle
Pour quelle position du point M, le rectangle inscrit dans le triangle rectangle OAB a t'il une aire maximale ?
Fonction longueur du rectangle
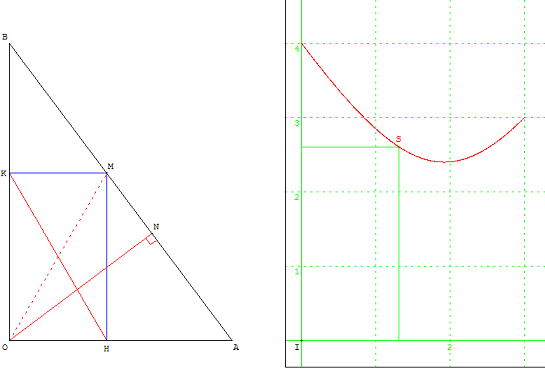
Solution
La résolution s'appuie sur l'isométrie des diagonales d'un rectangle et sur la notion de distance d'un point à une droite.
Le point solution est le pied de la hauteur issue de l'angle droit.
Télécharger la figure GéoPlan balade_hypotenuse.g2w
6. Lieu de point : diagonale mobile
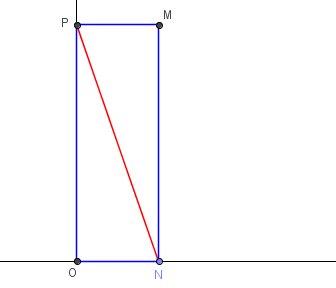
O est un point d'une droite (d1).
Une demi-droite (d2) est perpendiculaire en O à la droite (d1).
N est un point variable sur la droite (d1) et P est un point variable sur la demi-droite (d2) tels que PN = 5 cm.
On trace le point M tel que ONMP soit un rectangle.
Quel est le lieu géométrique du point M lorsque l'on déplace les points N ou P ?
Voir L@ feuille à problèmes : Transformations d'un problème
un lieu mystérieux : revue.sesamath.net – le LGD mène l'enquête
Autre diagonale rayon d'un demi-cercle
La résolution s'appuie sur l'isométrie des diagonales d'un rectangle.
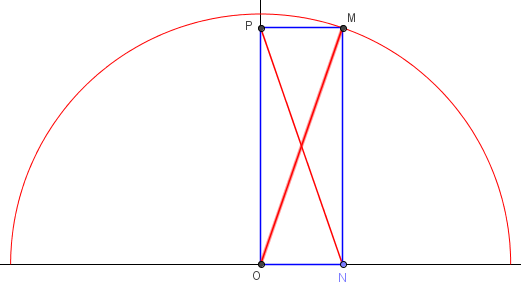
La construction d'un segment de longueur constante dont les extrémités sont mobiles sur des perpendiculaires nécessite la construction d'un cercle de rayon 5 cm, par exemple celui de centre N.
Le lieu solution est un demi-cercle de centre O et de rayon 5 cm.
Figure interactive dans GeoGebraTube : diagonale mobile d'un rectangle
7. Quadrilatère dans un rectangle : napperon
Petit x no 80
Sur une table rectangulaire ABCD, on veut placer un napperon ayant la forme d'un quadrilatère MNPQ. On souhaite que l'aire du napperon soit égale à la moitié de l'aire de la table.
Les sommets du napperon sont situés sur les côtés du rectangle avec M un point de [AB], N un point de [BC], P un point de [CD] et Q un point de [DA].
7.a. Réaliser une figure en utilisant un logiciel de géométrie (pour les sommets du rectangle, choisir la longueur L et la largeur l de telle façon que les coordonnées de A, B, C et D soient entières).
Quadrilatère
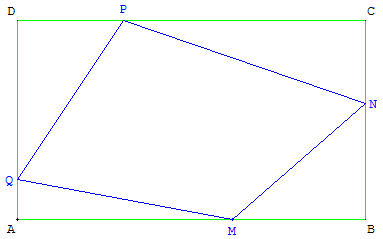
Parallélogramme
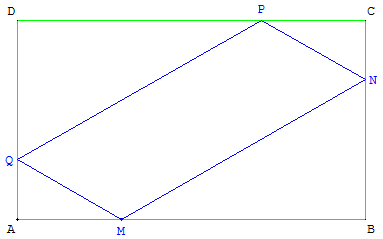
Variante : le napperon est un parallélogramme dont les côtés sont parallèles aux diagonales du rectangle.
Télécharger la figure GéoPlan Napperon.g2w,
la figure GéoPlan Napperon_parallelogramme.g2w
Remarque : ce parallélogramme minimise alors le périmètre des parallélogrammes inscrits dans le rectangle.
C'est le parallélogramme de lumière dont les côtés se réfléchissent sur les bords du rectangle à la façon de rayons lumineux.
7.b. Afficher les aires de rectangle ou de quadrilatère
Afficher l'aire du rectangle ABCD et l'aire du quadrilatère MNPQ.
Technique GéoPlan : on partage la surface des quadrilatères, avec une diagonale, en deux triangles et on additionne les aires :
« Créer > Affichage> Aire d'un triangle »
r1 aire du triangle ABC r = 2r1 t1 aire du triangle MNP t2 aire du triangle MPQ t = t1+t2
7.c. En faisant varier la position des points M ou P, émettre une conjecture concernant une condition suffisante pour que l'aire du quadrilatère MNPQ soit la moitié de celle du rectangle ABCD.
7.d. Démontrer le résultat conjecturé.
8. Taille d'une bille inscrite dans un rectangle
Calculer l'aire de la surface hachurée.
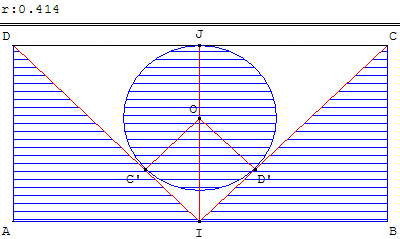
AB = 2, BC = 1.
Le cercle a pour rayon r = 
– 1.
L'aire de la surface hachurée est π(3 – 2) + 1.
Télécharger la figure GéoPlan bille.g2w
Table des matières
Dans d'autres pages du site
Au collège
Construire un rectangle connaissant la longueur d'un côté et de la diagonale
Partages en trois du rectangle
Point variable dans un rectangle
Euclide : partage en deux d'un rectangle avec quatre rectangles
Au lycée
Calculs d'aires dans un rectangle
Triangle inscrit dans un rectangle : pliage du coin d'une feuille, un devoir qui ne fait pas un pli !
Droites perpendiculaires dans un rectangle (ayant le format du papier A4)
Rectangle d'aire maximale
Aire maximale d'un rectangle inscrit dans un triangle rectangle – démonstration avec une parabole – démonstration géométrique
Aire minimale d'un triangle inscrit dans un rectangle
Aire maximale d'un rectangle inscrit dans un trapèze
1S : Rectangle inscrit dans un rectangle
Rectangle maximal inscrit dans un triangle isocèle
Carré d'aire maximale : olympiades Versailles 2005
Google friendly
|
|
Page no169, réalisée le 24/3/2011 |