 Descartes et les Mathématiques
Descartes et les Mathématiques
Construction géométrique au collège
Losange, quadrature du rectangle.
Exercices de construction géométrique
1. Losange
3. Carré dont les côtés passent par quatre points
4. La quadrature du rectangle
Sulbasutras
Figure d'Euclide
Construction de Wallis
Méthode de Samuel Marolois
Un programme de construction est un texte qui
permet d'établir une figure géométrique.
C'est souvent ainsi que débute un problème de géométrie
au collège ou au lycée.
C'est d'abord un exercice de lecture.
L'exécution demande du soin et aboutit à une validation complète :
l'observation d'une propriété de la figure.
Cette propriété est justifiée ultérieurement.
On établit ainsi une continuité entre un capital d'observations
et d'expériences et, plus tard, des preuves qui tissent
entre elles un réseau rationnel (François Boule).
1. Losange
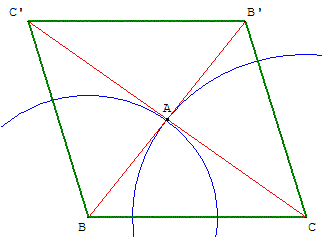
Construire un quadrilatère connaissant
les longueurs d'un côté et des diagonales.
Application : côté de longueur 5 et diagonales de longueurs 6 et 8.
Tracer un triangle dont les côtés ont pour longueurs AB = 3, AC = 4 et BC = 5.
Tracer les symétriques B’ et C’ de B et C par rapport à A.
Que peut-on dire du quadrilatère BCB’C’ ?
Indications
Le quadrilatère BCB’C’ admet A comme centre de symétrie,
c'est un parallélogramme.
Par la réciproque de la propriété de Pythagore,
le triangle ABC est rectangle en A.
Les diagonales de BCB’C’ sont perpendiculaires,
ce parallélogramme est un losange.
2. Point de concours
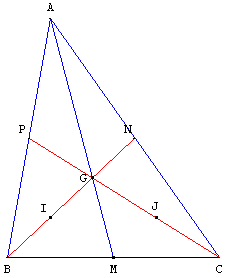
Soit un segment [BC]
et un point G non situé
sur (BC).
Tracer les milieux de [BG]
et de [CG] ainsi que le milieu M de [BC].
Prolonger [BG] d'une
longueur GN = BG/2
et [CG] d'une longueur GP = CG/2.
Prolonger [BP] et [CN].
Qu'observe-t-on ?
Indications
Les droites (BP) et (CN) se rencontrent en A sur (GM) :
de plus BP = PA, CN = NA et AG = 2 GM.
Ceci résulte de la propriété du centre de gravité G du triangle ABC.
3. Carré dont les côtés passent par quatre points
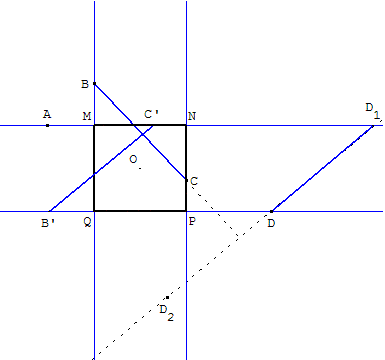
On donne quatre points A, B, C, D. Construire
quatre droites, passant par chaque point, de
telle sorte quelles déterminent un carré.
Problème assez difficile ne faisant malgré
tout appel qu'à des connaissances de troisième.
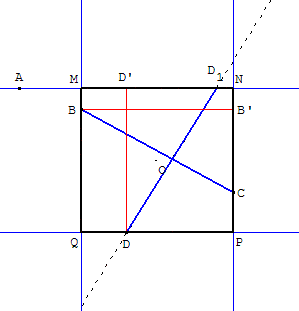
Supposons le problème résolu. MNPQ est le carré cherché de centre O.
Dans la rotation d'un quart de tour de centre O,
B a pour image B’ et C a pour image C’.
B’C’ = BC ; BC et B’C’ faisant un angle de 90°.
Comme B et C sont sur les droites portées par
deux côtés du carré, les images B’ et C’ sont sur
les deux autres droites portées par les deux autres côtés perpendiculaires.
Par la translation qui transforme B’ en D,
le point C’ a pour image un point D1 situé sur la
droite (AC’). B’DD1C’ est un parallélogramme
[DD1] étant parallèle et égal à [B’C’].
Donc, (DD1) est perpendiculaire à (BC) avec DD1 = BC.
Carré MNPQ
On peut donc construire un point D1 sur la
perpendiculaire à (BC) passant par D, à une
distance égale à BC de D.
On obtient la première droite (AD1),
les trois autres droites étant parallèle ou perpendiculaires à (AD1).
Carré M’N’P’Q’
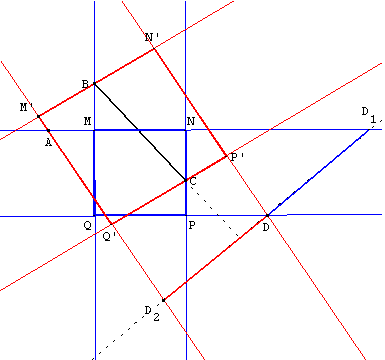
On obtient un deuxième carré M’N’P’Q’ avec l'autre
point D2, à une distance égale à BC de D,
sur cette même perpendiculaire.
Démonstration :
par construction, MNPQ est un rectangle (trois angles droits).
Deux côtés consécutifs de MNPQ ont la même longueur ?
Soit B’ le projeté orthogonal de B sur (NP) et D’
le projeté orthogonal de D sur (MN).
Les triangles rectangles B’BC et D’DD1 ont
leurs côtés deux à deux perpendiculaires.
L'hypoténuse [BC] est perpendiculaire à [DD1] avec BC = DD1.
Les triangles sont égaux et BB’ = DD’.
Ce qui prouve que deux côtés consécutifs
ont même longueur : MNPQ est un carré.
4. Cinq quadratures du rectangle
Construire un carré de même aire qu'un rectangle
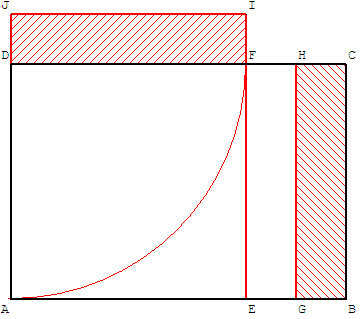
4.a. Sulbasutra
Textes rituels de l'Inde, rédigés en sanskrit vers le VIIIe siècle avant J.-C.,
issus de tradition orale remontant à plus de 2000 ans avant notre ère.
Dans le rectangle ABCD, reporter la largeur pour obtenir le carré AEFD.
Partager en deux parties égales le rectangle EBCF
excédentaire et déplacer le demi-rectangle GBCH en DFIJ.
Dans la figure ci-contre, compléter la place vide pour obtenir le carré AGKJ.
Le cercle de centre J, passant par A coupe [DH] en L.
[DL] est le côté du carré de même aire que le rectangle.
Sulbasutras :
construction du carré à partir d'une médiatrice
constructions de carrés d'aire égale à la somme
ou la différence des aires de deux carrés
Preuve moderne avec ce que nous appelons
le théorème de Pythagore.
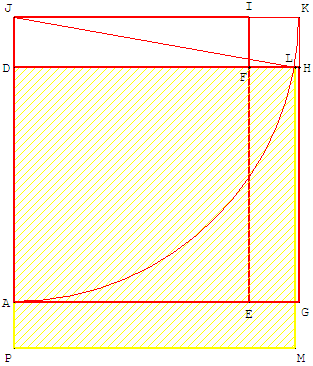
Si la longueur du rectangle est AB = 2a et la largeur BC = 2b,
alors DH = JL = a + b et JD = a – b.
Dans le triangle rectangle JDL, la relation de Pythagore
permet de trouver la différence des carrés DL2 = JL2 – JD2.
Soit DL2 = (a + b)2 – (a – b)2 = 4ab = AB × BC.
4.b. Les Éléments d'Euclide - Livre II - Proposition 14
Faire un carré égal à une figure donnée
Figure d'Euclide
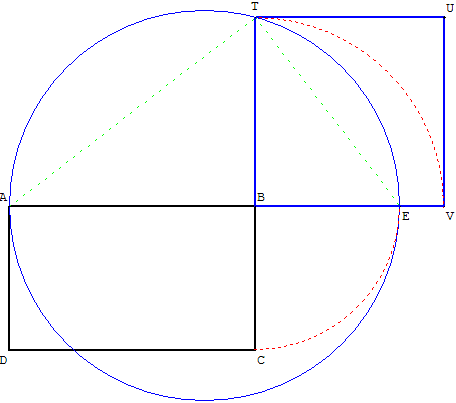
Pour cette construction d'un carré BTUV de même
aire que le rectangle ABCD,
utiliser le théorème de la hauteur dans le triangle ATE,
rectangle en T, inscrit dans le demi-cercle de diamètre [AE].
Si B le pied de la hauteur issue de T, alors le carré de
la hauteur BT est égal au produit des segments
AB et BE découpés sur l'hypoténuse : BT2 = BA × BV.
En l'interprétant de manière géométrique,
cette relation permet de construire un carré de côté
[BT] de même aire qu'un rectangle de côtés [BA] et [BV].
Construction d'Euclide, reprise par Descartes :
Sur la longueur (AB), on reporte la largeur du rectangle
en E et on trace le cercle qui admet ce côté prolongé
[AE] pour diamètre.
L'intersection du prolongement de la largeur
(le long de BC) avec ce cercle définit la hauteur
[BT], l'un des côtés du carré BTUV.
Le carré BTUV a même aire que le rectangle ABCD.
Voir : quadrature du triangle équilatéral
Dans les Éléments d'Euclide, voir aussi :
II 11. Carré et rectangle de même aire
4.c. Rectangle et carré côte à côte
Félix Klein - Problèmes célèbres de la géométrie élémentaire
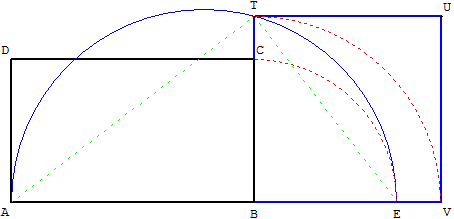
Sur (AB), on reporte la largeur en E. (BC) coupe
le demi-cercle de diamètre [AE] en T.
Avec le cercle de centre B, passant par T,
on reporte la longueur BT en BV, avec le point V
sur la droite (AB), à l'extérieur du segment [AB].
Avec le point U, on termine la construction du
carré BTUV de côtés [BT] et [BV], de même aire que le rectangle.
Ci-dessous, la construction de Marolois où les deux
quadrilatères sont d'un même côté de (BC).
4.d. Construction de Wallis
Construire un carré de même aire qu'un rectangle donné.
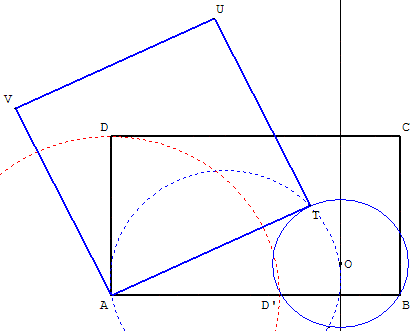
ABCD un rectangle de longueur [AB]. Rabattre D en D’ sur [AB].
Tracer un cercle quelconque passant par D’ et B,
puis la tangente AT à ce cercle.
Démonstration (après le bac) :
La puissance du point A par rapport au cercle est
AT2 = AD’ × AB = AD × AB.
Le carré ATUV de côté [AT] répond à la question.
4.e. Méthode de Samuel Marolois (1617)
Transformer le rectangle ABCD en un carré,
de même aire, bordé par les droites (AB) et (BC).
Réalisation à l'aide d'un compas et d'une règle non graduée.
Solution
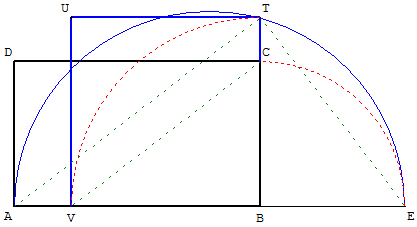
Le long de (AB), on prolonge la longueur du rectangle
d'un segment [BE] égal à sa largeur, et on trace le
demi-cercle qui admet ce côté prolongé pour diamètre.
L'intersection du prolongement de la largeur
(le long de BC) avec ce demi-cercle définit [BT],
l'un des côtés du carré.
Première construction avec un cercle
Le cercle de centre B, passant par T, coupe [AB] en V.
Avec le point U, on termine la construction du carré
BTUV de côtés [BT] et [BV], de même aire que le rectangle.
Deuxième construction avec des parallèles
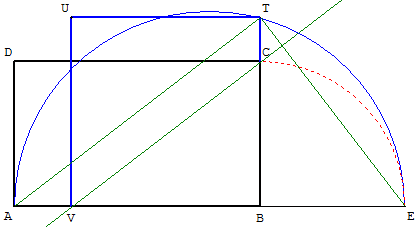
La droite parallèle à (AT), passant par C, coupe [AB] en V.
Le théorème de Thalès dans le triangle BTA permet d'écrire :
BV/BA = BC/BT, soit BV × BT = BA × BC = Aire(ABCD),
donc BV = BC = c est égal au côté du carré cherché.
V est un sommet du carré et, avec le point U, on termine
la construction de BTUV, de côtés [BT] et [BV],
de même aire que le rectangle.
Construction réciproque
Construction d'un rectangle de largeur l,
ayant même aire qu'un carré de côté c (l < c).
Sur le côté [BT] d'un carré BTUV de côté c, placer un point C tel que BC = l.
La droite parallèle à (CV), passant par T, coupe (BV) en A.
Avec le sommet D, terminer la construction du rectangle,
de même aire que le carré.
En effet, comme ci-dessus, Aire(ABCD) = BA × BC = BV × BT = c2.
4.f. Construction avec un triangle rectangle
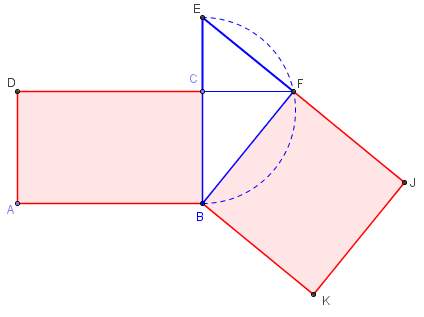
À partir d'un rectangle ABCD, reporter la longueur
du rectangle sur [BC) en y plaçant le point E, tel que BE = AB.
Prolonger [DC) jusqu'au demi-cercle de diamètre [BE],
en F à l'extérieur de [DC].
[CF] est la hauteur du triangle rectangle BEF.
Dans ce triangle rectangle, le côté BF de l'angle
droit est moyenne proportionnelle entre
l'hypoténuse et sa projection sur l'hypoténuse.
BF2 = BE × BC.
Le carré BFJK a pour aire BF2 égale à BE × BC = AB × BC,
soit l'aire du rectangle.
![]() Figure interactive dans GeoGebraTube : quadrature du rectangle
Figure interactive dans GeoGebraTube : quadrature du rectangle
Dans d'autres pages du site
Construction à l'équerre
Construction du pentagone régulier
Théorème de Thalès en 3e
Démonstrations géométriques de Pythagore
Sur ordinateur, cette page en grand écran
![]() Mobile friendly
Mobile friendly
La première page de ce document n'est pas une image
et une copie ne devrait pas être référencée par Google !
Copyright 2003 - © Patrice Debart
|
. |
Page no 59, réalisée le 6/12/2003 |