Descartes et les Mathématiques

Triangle équilatéral

Constructions du triangle équilatéral :
Euclide, pliages, construction avec contraintes.

Sommaire

1. Construction à la règle et au compas

2. Construction de deux triangles isocèles

3. Cercles et triangle équilatéral

4. Construire un triangle équilatéral
        – dont deux des sommets sont situés sur deux droites

        – dont les sommets sont situés sur des cercles concentriques
5. Relation métrique

6. D'un triangle équilatéral à l'autre

7. Triangle et cercle inscrits

8. Triangle équilatéral inscrit dans un triangle

9. Triangle équilatéral circonscrit à un triangle

Équilatéral : du latin aequi, égal et latus, côté.
Les Grecs utilisaient le mot isopleure : qui a ses côtés égaux.

Propriétés du triangle équilatéral

Les trois propositions suivantes sont équivalentes :

  • un triangle a ses trois côtés de même longueur,
  • un triangle a ses trois angles de même mesure,
  • un triangle a trois axes de symétrie.

Le triangle est alors dit équilatéral ou régulier.

Les trois angles d'un triangle équilatéral sont égaux et mesurent 60°
(soit radians).

Pour monter qu'un triangle est équilatéral, on peut, au choix, vérifier que :

  • les trois côtés sont de même longueur,
  • il a deux angles de 60°,
  • il est isocèle avec un angle de 60°,
  • il a deux axes de symétrie,
  • …

Droites remarquables du triangle équilatéral, hauteur

Dans un triangle équilatéral, toutes les droites remarquables
(médiane, hauteur, bissectrice, médiatrice) relatives
à un même côté sont confondues.

Hauteur d'un triangle équilatéral

Les droites remarquables ont même longueur, égale à h = a,
où a est la longueur du côté du triangle.

Calcul de l'aire du triangle équilatéral : a × h égale à a².

Le centre de gravité est confondu avec l'orthocentre
et les centres des cercles inscrit et circonscrit.

Théorème de Viviani : Dans un triangle équilatéral,
la somme des distances d'un point intérieur au triangle
aux trois côtés est égale à la hauteur du triangle.

Propriété qui se démontre en décomposant l'aire du triangle ABC
en somme des aires des trois triangles ayant pour sommet le point
intérieur P et un des des côtés du triangle :triangles PAB, PBC, PCA.

Rayon du cercle circonscrit au triangle équilatéral

Le rayon R = OA du cercle circonscrit est égal aux
de la longueur de la médiane, soit R = a ,
on en déduit la longueur du côté a = R.

Rayon du cercle inscrit dans un triangle équilatéral

Le rayon r = OH du cercle inscrit est égal au
de la longueur de la médiane, soit r = a,
d'où la longueur du côté a = 2r et
le rayon du cercle circonscrit R = 2r.

Dans un triangle équilatéral, le cercle circonscrit
a un rayon double de celui du cercle inscrit.

Quadrature du triangle équilatéral

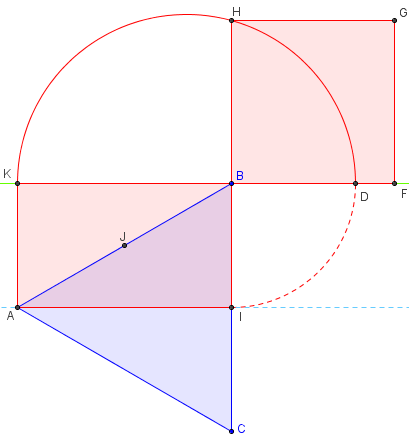
Construire, à la règle et au compas, un carré
ayant la même aire que le triangle équilatéral.

Soit ABC un triangle équilatéral. Notons I
le milieu du segment [BC] et J le milieu de [AB].

La médiatrice (AI) de [BC] partage le triangle
en deux triangles rectangles de même aire.

La symétrie de centre J transforme le
triangle rectangle AIB en BKA.
Le triangle équilatéral ABC et rectangle AIBK, formés
par deux triangles rectangles isométriques, ont même aire.

Il s'agit donc, avec une figure d'Euclide,
de construire un carré de même aire que ce rectangle.

Pour cela, nous allons utiliser le théorème de la hauteur
dans le triangle rectangle KHD, rectangle en H,
inscrit dans le demi-cercle de diamètre [KD].
Si B le pied de la hauteur issue de H, alors BH² = BK × BD.

En l'interprétant de manière géométrique, cette relation permet
de construire un carré de côté [BH] de même aire qu’un
rectangle de côtés [BK] et [BD].

Sur la longueur (KB), on reporte la largeur du rectangle en D
et on trace le demi-cercle qui admet ce côté prolongé [KD]
pour diamètre.
L'intersection du prolongement de la largeur, le long de (BI),
avec ce cercle définit la hauteur [BH], l'un des côtés du carré BHGF.

Le carré BHGF a même aire que le triangle équilatéral ABC
(ainsi que le rectangle AIBK).

On retrouve bien le calcul de l'aire du triangle équilatéral :
A = BK × BD = a × a = a².

Figure interactive dans GeoGebraTube :
        quadrature du triangle équilatéral

Il est possible de remplacer le triangle équilatéral
par un triangle isocèle en A.

1. Construction du triangle équilatéral

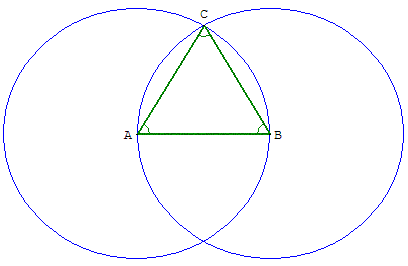
Tracer un triangle équilatéral avec un logiciel de géométrie dynamique

Collège : classes de sixième et cinquième

Placer A et B et tracer le segment [AB],
tracer les cercles de centre A passant par B et de centre B passant par A,
construire C, un des points d'intersection des deux cercles,
terminer en traçant les segments [BC] et [AC].

Figure interactive dans GeoGebraTube : triangle équilatéral

Voir : construire un triangle équilatéral sur une ligne
droite donnée et finie dans les Éléments d'Euclide

1.b. Deux triangles équilatéraux symétriques

Construction de deux triangles équilatéraux symétriques,
entre deux cercles de même rayon.

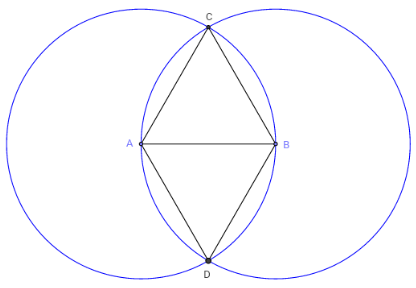
Placer A et B et dessiner le segment [AB],
tracer les cercles de centre A passant par B et de centre B passant par A,
construire C, un des points d'intersection des deux cercles,
terminer en traçant les segments [BC] et [AC].

Figure interactive dans GeoGebraTube :
        deux triangles équilatéraux

2. Construction de deux triangles isocèles

Construction à partir de deux sommets : le triangle équilatéral
ABC peut être construit comme triangle isocèle en C tel que
CA = CB et comme triangle isocèle en A tel que AB = AC.

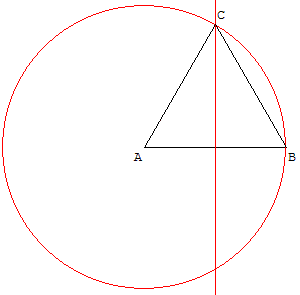
À partir de deux points A et B, il possible de tracer le triangle
équilatéral ABC comme triangle isocèle à partir de la base,
en traçant la médiatrice de [AB],
puis comme triangle isocèle à partir d'un des côtés égaux,
en traçant le cercle de centre A passant par B.

Le point C est alors un des points d'intersection de la
médiatrice de [AB] et du cercle de centre A passant par B.

3. Cercles et triangle équilatéral

Classe de seconde

Construction d'un triangle équilatéral inscrit dans u
n cercle, grâce à un deuxième cercle de même rayon

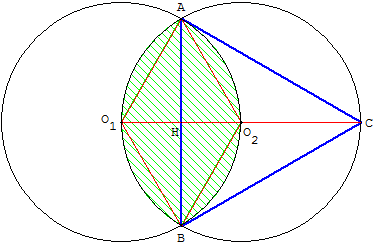
Les cercles (c₁) de centre O₁ et (c₂) de centre O₂
ont même rayon R ; le centre de l'un appartient à l'autre.
Le point C est le symétrique de O₁ par rapport à O₂.
Les deux cercles se coupent en A et B.

  • Montrer que le triangle ABC est équilatéral de côté R .
  • Le cercle (c₂) est circonscrit au triangle équilatéral ABC.

Indications : les triangles AO₁O₂ et BO₁O₂ sont équilatéraux
(configuration de la figure 1).
L'angle au centre AO₂B est égal à 120°.
L'angle inscrit ACB mesure 60°.
Le triangle ABC ayant la droite (CO₁) comme axe de symétrie
est isocèle.
Un triangle isocèle ayant un angle de 60° est équilatéral.

Voir le premier paragraphe pour le calcul R
de la longueur du côté.

Voir le calcul du périmètre et de l'aire de la surface hachurée
formée par les deux segments circulaires de part et d'autre
de la corde [AB].

Application :
dessiner un triangle équilatéral inscrit dans un cercle

Dans un cercle (c₂) de centre O₂, tracer un diamètre [O₁B].
Soit H le milieu H de [O₁O₂].
Par H, tracer la médiatrice de [O₁O₂] qui coupe le cercle en A et B.

  • Le triangle ABC est équilatéral.

4. Triangle équilatéral avec contraintes

4.a. Un triangle dont deux sommets sont sur une droite

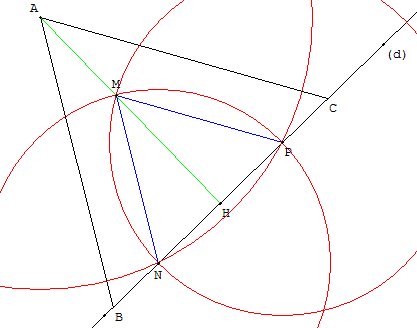
Étant donné un point A et une droite (d), tracer un triangle
équilatéral ABC, tel que les sommets B et C soient situés sur la droite (d).

Indication

À partir d'un point N de la droite (d) construire, à la « règle et
au compas », un triangle équilatéral MNP qui permettra, par
agrandissement-réduction de trouver le triangle ABC.

Pour cela, on peut :

Placer un point N sur la droite (d).
Le cercle de centre A passant par N recoupe la droite (d) en P.
Les cercles de centre N passant par P et de centre P passant
par N se coupent en M.
MNP est un triangle équilatéral.
Les points A et M étant équidistants de N et P, la droite (AM),
médiatrice de [NP], est hauteur du triangle MNP
et du triangle ABC cherché.

Les parallèles à (MN) et (MP) passant par A coupent (d) en B et C.
Le triangle équilatéral ABC est la solution.

4.b. Triangle avec deux sommets sur deux droites

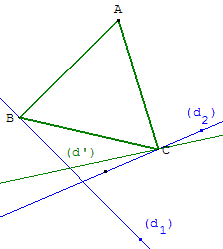
On donne un point A et
deux droites (d₁) et (d₂).

Existe-t-il un point B sur
(d₁) et un point C sur (d₂)
tel que le triangle ABC
soit équilatéral.

Solution : deux sommets du triangle sur deux droites

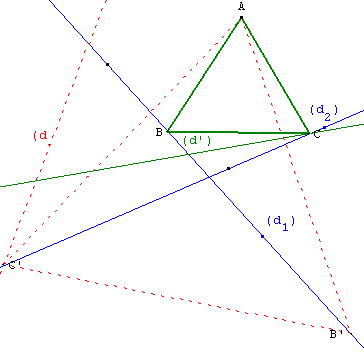
Si le triangle équilatéral ABC existe, le point C est obtenu
à partir du point B par une rotation de 60° (ou de - 60°)
autour de A. Cela nous donne une méthode de construction de
eux triangles qui, en général, répondent à la question :

– Premier triangle : on fait pivoter la droite (d₁) de 60°
autour de A. La transformée (d₁’) coupe (d₂) en C.
Le point de (d₁) dont C est l'image est le point B.
– Deuxième triangle : on fait pivoter la droite (d₁)
de - 60° autour de A. La transformée (d₁’) coupe
(d₂) en C. Le point de (d₁) dont C
est l'image est le point B.

Dans le cas où (d₁) et (d₂) font entre elles un angle de 60°,
l'une des deux constructions reste valable. Quant à l'autre,
elle en génère une infinité ou au contraire ne produit
aucun triangle selon que A est sur des bissectrices
de (d₁, d₂) ou pas.

Construction du triangle avec deux sommets sur deux droites

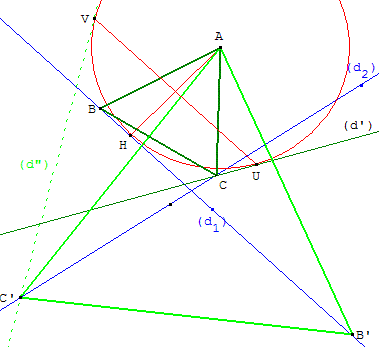
Soit H la projection de A sur la droite (d₁), on construit le
cercle (c) de centre A, tangent à (d₁) en H.
La médiatrice de [AH] coupe le cercle (c) en U et V.
Les tangentes en U et V sont les images de (d₁) par les rotations
d'angles 60° et -60°. Ces deux tangentes coupent, en
général, (d₂) en deux points C et C’.
On construit les antécédents B et B’ de C et C’ dans les deux rotations.

4.c. Problème des trois parallèles

Construire un triangle équilatéral dont les
sommets sont situés sur trois droites parallèles

Étant donné trois droites parallèles (d₁), (d₂) et (d₃),
choisir un point A sur (d₁) et le problème devient « tracer un
triangle équilatéral de sommet A tel que les deux autres
sommets soient situés sur deux droites parallèles. »

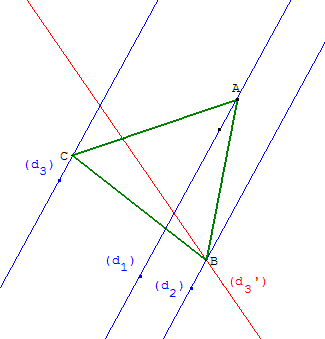
Méthode 1 - rotation

Construire l'image (d₃’) de la droite (d₃) par la rotation r
de centre A et d'angle 60°, cette droite image (d₃’)
coupe (d₂) en B.
Enfin, on obtient le point C en construisant l'image de B par l
a rotation réciproque r^{– 1} de centre A et d'angle -60°
(constructions faciles, avec la règle et le compas).

Démonstration

(d₃’) coupe bien (d₂) : en effet, l'angle entre (d₃) et (d₃’) étant
de 60° (ou 120°), et (d₂) et (d₃) étant parallèles, l'angle entre
(d₂) et (d₃’) est donc de 60° (ou 120°).
Le point C appartient bien à (d₃) car C est l'image de B par r^{– 1} ;
B appartient à (d₃’) et l'image de (d₃’) par r^{– 1} est (d₃).
Enfin, ABC est bien équilatéral, car C est l'image de B par
la rotation réciproque r^{– 1} de centre A et d'angle -60°,
donc ABC est isocèle en A et d'angle au sommet 60°,
ces trois angles valent donc chacun 60°.

« Où l'on construit un triangle équilatéral »
« Où l'on calcule l'aire de ce triangle équilatéral » :
voir exercice bac S centres étrangers 1998

Méthode 2 - cercle circonscrit

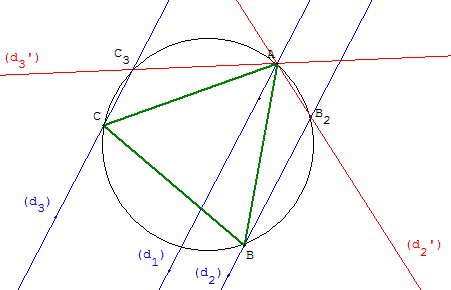
Construire un triangle équilatéral dont les sommets son
situés sur trois droites parallèles (d₁), (d₂) et (d₃).

On peut choisir arbitrairement un point A sur la droite (d₁)
- figure plus simple en choisissant la droite du centre comme
droite (d₁).

Démonstration : À partir du point A tracer les droites (d₂’)
et (d₃’) faisant avec la droite (d₁) des angles de 60°
(utiliser les images d'un point de (d₁) par les rotations
de centre A et d'angles 60° et -60°).

(d₂’) coupe (d₂) en B₂ et (d₃’) coupe (d₃) en C₃.
Le cercle circonscrit au triangle AB₂C₃ recoupe (d₂) en B
et (d₃) en C. Les angles inscrits AB₂B et AC₃C, égaux à 120°,
interceptent sur le cercle deux arcs dont les longueurs sont
égales au tiers de la circonférence. Les angles inscrits
supplémentaires ACB et ABC sont égaux à 60° et le triangle
ABC est une solution du problème.

Problèmes analogues

Construire un triangle rectangle isocèle dont :
  • les deux sommets des angles aigus sont situés sur deux droites,
  • le sommet de l'angle droit est situé sur une droite,
un des sommets d'un angle de 45° est situé sur une autre droite.

4.d. Problème des trois cercles

Tracer un triangle équilatéral dont les sommets
sont situés sur trois cercles concentriques

Construire un triangle équilatéral ABC connaissant les
distances a, b, c de ses sommets A, B, C à un point O donné.

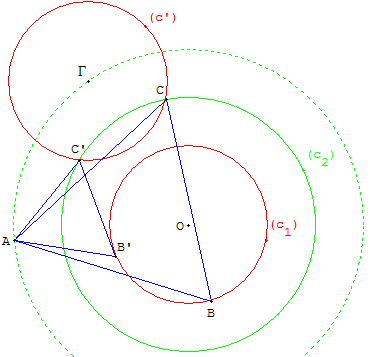
On peut choisir arbitrairement un point A tel que OA = a
et le problème devient « construire un triangle
équilatéral de sommet A tel que les deux autres
sommets soient situés sur deux cercles
concentriques (c₁) et (c₂) de centre O et de rayons b et c. »

Construire l'image (c’) du cercle (c₁) par la rotation r
de centre A et d'angle 60°.
Si l'on peut tracer un triangle dont les côtés mesurent a, b, c ;
ce cercle image (c’) coupe le cercle (c₂) aux points C et C’.
Enfin, on obtient les points B et B’ en construisant les images
de C et C’ par la rotation réciproque r^{– 1} de centre A et d'angle – 60°.

On obtient ainsi deux triangles équilatéraux ABC et A’B’C’.
Par symétrie autour de la droite (AO) on trouve deux autres
solutions, soit quatre solutions pour un sommet donné.

Cas particulier

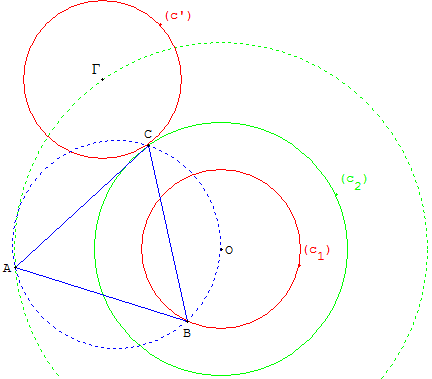
Si le triangle dont les côtés mesurent a, b, c est aplati (ici a = b + c) ;
ce cercle image (c’) est tangent au cercle (c₂) en C.

On obtient ainsi un triangle équilatéral ABC.

Les quatre points O, A, B, C sont cocycliques.

On en déduit que, si O est un point du cercle
circonscrit à un triangle équilatéral ABC,
l'une des longueurs OA, OB, OC est la
somme des deux autres.

5. Relation métrique MA = MB + MC

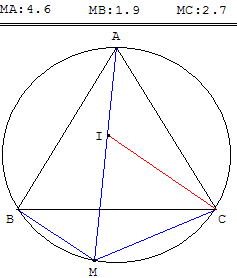
Classe de seconde

ABC est triangle
équilatéral.
M un point du cercle
circonscrit (c),
M est entre B et C.

Montrer que
MA = MB + MC.

Indication

Soit I le point de [AM]
équidistant de M et C.
MIC triangle isocèle ayant un angle de 60°
(angle inscrit AMC dans le cercle (c) égal l'angle ABC),
est aussi équilatéral.

La rotation de centre C et d'angle 60° transforme I en M et A en B.
Donc, IA = MB et MB + MC = IA + IM = MA.

Bissectrice

Une étude des angles inscrits permet de remarquer
que BMC complémentaire de BAC mesure 120°,
que AMB = ACB = 60° et AMC = ABC = 60°,
(MA) est la bissectrice de BMC.

6. D'un triangle équilatéral à l'autre

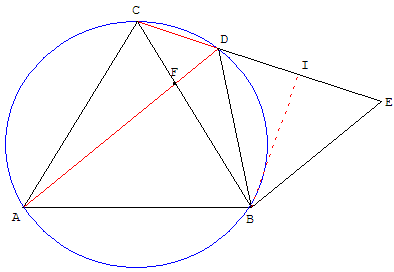
Classe de seconde

ABC est un triangle équilatéral inscrit dans un
cercle (c).

F est le point de [BC] tel que FB = k FC.
On choisira k = 1, 2 ou 3.

La droite (AF) recoupe le cercle en D.
La droite parallèle à (AD) passant par B coupe (CD) en E.

6.a. Montrer que le triangle BED, ayant deux angles de 60°,
est un triangle équilatéral.
Vérifier que et calculer DF.
6.b. Calculer le rapport de l'aire du triangle ABC
sur l'aire du triangle BED.

Indications

6.a. Les angles inscrits ADC et ADB sont égaux à 60°.
(DF) est une bissectrice du triangle
BCD et DB/DC = FB/FC = k, soit DB = k DC.

Le triangle BED, ayant deux angles de 60°,
est un triangle équilatéral ; on note a son côté :
DB = DE = a et DC = a/k.

Par hypothèse (FD) // (BE), d'après la propriété
de Thalès dans le triangle BCE on a : CE/CD = BE/FD.

1/DC + 1/DB = 1/DC + 1/DE = (DE + DC) / (DC×DE)
= CE / (CD×DE) = CE/CD × 1/DE = BE/FD × 1/DE = 1/FD.

On a donc .

De DB = k DC = a, on trouve 1/DF = 1/DB + k/DB = (k + 1)/DB,
d'où DF = DB/(k + 1) ; soit DF = a/(k + 1).

6.b. Soit I le milieu de [DE]. La hauteur de BED est IB = a.

CI = CD + DI = a/k + a/2 = a (1/k + ). Avec la
relation de Pythagore dans le triangle rectangle BCI :

CB² = CI² + IB² = a²((1/k + )² + ) = a² ,
le rapport de l'aire du triangle ABC sur l'aire du
triangle BED est égal au rapport des carrés de
leurs côtés, donc .

Pour k = 2 on a un rapport de 7/4.

7. Triangles équilatéraux et cercles inscrit et circonscrit

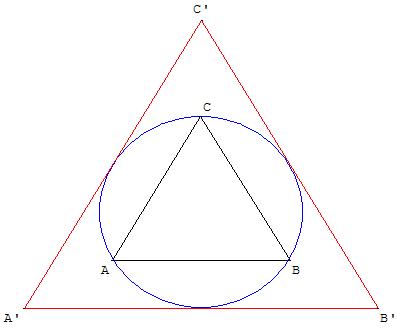
Un triangle équilatéral est inscrit dans un cercle,
lui-même inscrit dans un autre triangle équilatéral.

La longueur du côté du petit triangle étant 1,
quelle est celle du côté du grand ?

Solution

Tracer le triangle médian A₁B₁C₁ de A’B’C’.
Ce triangle équilatéral inscrit dans le cercle
a ses côtés de longueur 1.

Le triangle A’B’C’ est alors décomposé en quatre
triangles équilatéraux de même taille que ABC.
Le côté A’B’ = A’C₁ + C₁B’ = 1 + 1 = 2
du grand triangle est double de celui du petit.

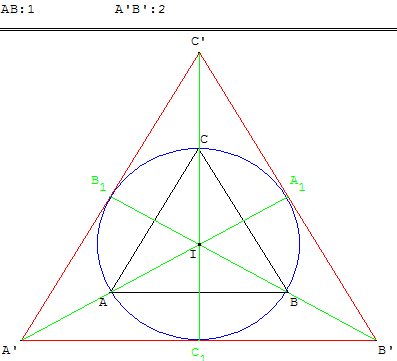
Le cercle circonscrit au triangle A’B’C’ a un rayon R,
double du rayon r du cercle circonscrit au triangle ABC.

Cercles inscrit et circonscrit

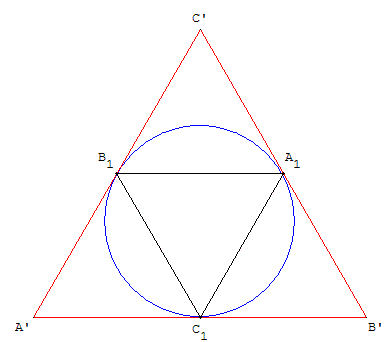
Le cercle circonscrit au triangle A₁B₁C₁
est le cercle inscrit dans le triangle. A’B’C’.

Les Éléments d'Euclide - livre IV - Proposition 1

figure de D. Henrion

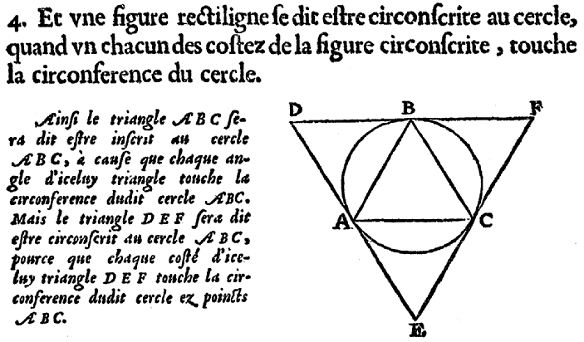
Remarque

Le cercle circonscrit au triangle DEF a un rayon R
double du rayon r du cercle circonscrit au triangle ABC.
Ce cercle est le cercle inscrit dans le triangle. DEF.

D'où : dans un triangle équilatéral, le cercle
circonscrit a un rayon double de celui du cercle inscrit..

Page précédente des Éléments, voir : triangle inscrit dans un triangle

Inscrire, circonscrire un triangle
équilatéral à un triangle

Classe de première L

8. Triangle équilatéral inscrit dans un triangle

9. Triangle équilatéral circonscrit à un triangle

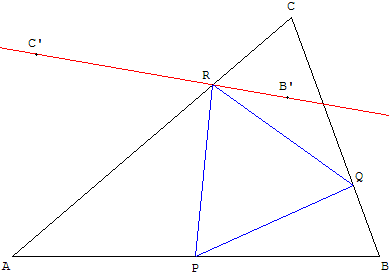
8. Triangle équilatéral inscrit dans un triangle donné

Construction s'appuyant sur des rotations.

Choisir un point P sur le côté [AB].
La rotation de centre P et d'angle 60°
transforme la droite (BC) en (B’C’).

Le point d'intersection R de [AC] et (B’C’),
s'il existe, est un point du triangle équilatéral cherché.
On trouve le troisième point Q, image de R
par la rotation réciproque d'angle – 60°.

Le triangle équilatéral PQR est inscrit dans le triangle ABC.

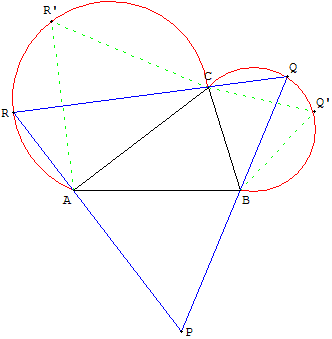
9. Triangle équilatéral circonscrit à un triangle donné

Construction s'appuyant sur des arcs capables.

Il s'agit de trouver des points Q et R tels que
de ces points, l'on « voit » les côtés [ BC] et
[AC] sous un an angle de 60°.

Pour cela, construire les triangles équilatéraux
BCQ’ et ACR’.
Les arcs capables sont situés sur les
cercles circonscrits à ces triangles.

Choisir un point Q sur l'arc BC.
La droite (QC) coupe l'arc AC en R.

Terminer le triangle équilatéral avec le sommet
P intersection des droites (QA) et (RA).

Table des matières

Dans d'autres pages du site

Triangle équilatéral inscrit dans un carré - aire maximale (Abul Wafa)

Construction d'un triangle équilatéral par pliage :
        – pliage d'une bande rectangulaire

        – pliage à partir d'un cercle

Triangle équilatéral à l'intérieur d'un carré au lycée :
carré et triangles équilatéraux - Prouver des alignements

Duplication du triangle équilatéral

Les problèmes du BOA

Triangles équilatéraux

    a. Triangles équilatéraux autour d'un quadrilatère

    b. Deux triangles équilatéraux autour d'un carré
        Triangles de Napoléon

Google friendly, sur ordinateur, cette page pour grand écran