Descartes et les Mathématiques

Calculs d'aires par découpage

Calculs d'aire en seconde avec GéoPlan : lunules, découpage avec deux triangles équilatéraux.

Sommaire

1. Duplication de figures

2. Lunule

3. Cercles et triangle équilatéral

4. Un partage équitable - Olympiades 2008 de première

1. Duplication de figures

Construire une figure semblable à une figure donnée, dont l'aire soit le double de celle de la figure donnée.

Duplication du carré

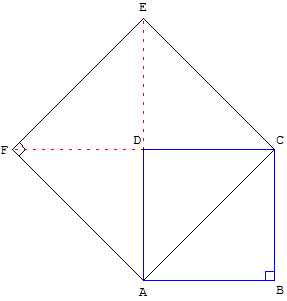
La diagonale du « petit carré » le partage en deux triangles isocèles rectangles. Le « grand carré » est formé de quatre triangles isocèles rectangles, de même aire.

L'aire du carré ACEF est le double de l'aire du carré ABCD.

Le rapport des côtés est , et va permettre, par similitude de
rapport ,les trois constructions suivantes.

Télécharger la figure GéoPlan duplication_carre.g2w

Retrouver cette figure dans les pages grands problèmes de la géométrie grecque ou carré au collège

Duplication du triangle équilatéral

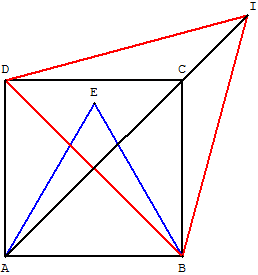
BD = AB.

Le rapport de similitude des triangles est .
Le rapport des aires est ² = 2.

L'aire du triangle équilatéral BDI est le double de celle du triangle équilatéral ABE.

 Télécharger la figure GéoPlan carre_2tr_equi.g2w

Retrouver cette figure dans la page montrer un alignement

Duplication du rectangle

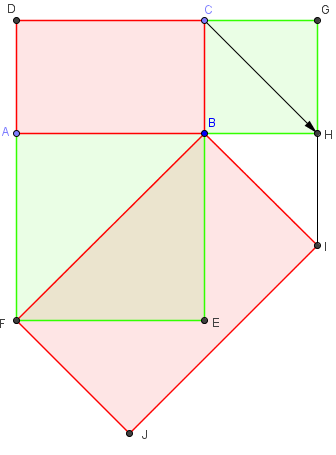
Tracer, le long du rectangle ABCD, deux carrés ayant pour côtés les longueur et largeur.

Le rectangle JIBF, ayant pour côtés les diagonales des carrés, a une aire double de celle de ABCD.

Figure interactive dans GeoGebraTube : duplication du rectangle

Duplication du triangle

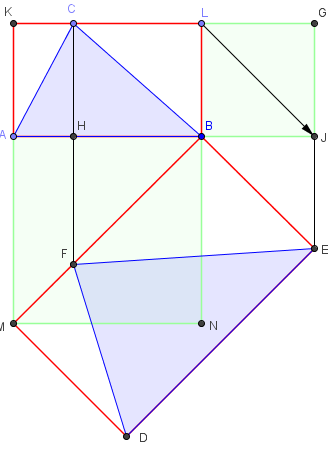
Tracer un rectangle BCLK contenant le triangle ABC.
Dupliquer, comme ci-contre, ce rectangle en DEBM.

La hauteur (AH) de ABC coupe [BM] en F.

Le triangle DEF, semblable à ABC, a une aire double de celui-ci ;
aires moitiés de celle des rectangles.

Figure interactive dans GeoGebraTube : duplication du triangle

Voir duplication du cercle d'Archimède

2. Lunule

Définitions : une lunule est une portion de surface délimitée par deux cercles non concentriques de rayons différents, formant un croissant de lune en forme de ménisque : convexe d'un côté et concave de l'autre.

Ici une lunule désigne aussi un segment circulaire (segment de cercle) : la portion de surface délimitée par un arc de cercle et sa corde.

Deux cercles

Concours EPF - 2002

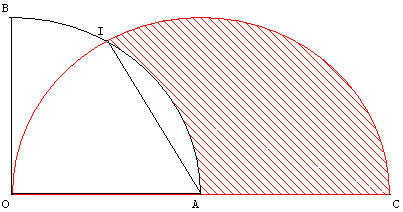
AB est un quart de cercle de rayon 1 et de centre O ; OC un demi-cercle de centre A et de même rayon. Soit I le point d'intersection du quart de cercle et du demi-cercle.

2.a. Calculer l'aire de la lunule déterminée par la corde IA sur le cercle de centre O.

2.b. Calculer l'aire de la surface hachurée.

Indications : 2.a. Les trois côtés de OIA sont des rayons des cercles :
OA = OI = IA = r = 1, OIA est équilatéral, son aire est r² = .
Le cercle de centre O a une aire égale à πr² = π. Le secteur angulaire, d'angle 60°, compris entre l'arc de ce cercle et les rayons [OA] et [OI] correspond à du cercle, son aire est .
L'aire de la lunule déterminée par la corde IA est − ≈ 0,09.

2.b. Le secteur angulaire, d'angle 120°, compris entre l'arc du cercle de centre A et les rayons [AI] et [AC] correspond à du cercle,
son aire est .

La surface hachurée, formée de ce secteur auquel on enlève la lunule, a pour aire − ( − ) = + ≈ 0,96.

2.c. Méthode des aires

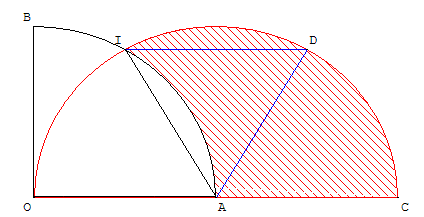En introduisant le point D, milieu de l'arc , on obtient un triangle équilatéral ADI d'aire et un secteur angulaire, d'angle 60°, compris entre l'arc du cercle de centre A et les rayons [AD] et [AC] correspondant à du cercle, son aire est .
Les lunules déterminées par la corde IA sur le cercle de centre O et celle déterminée par la corde ID sur le cercle de centre A ont même aire, car les cordes ont même longueur et les cercles même rayon.
En enlevant au triangle équilatéral la lunule déterminée par la corde IA et en ajoutant celle déterminée par la corde ID on obtient, avec le secteur angulaire DAC, la surface hachurée d'aire + .

Voir : lunules d'Hippocrate de Chios

Technique GéoPlan

Pour créer la surface hachurée, colorier le demi-cercle de diamètre [CO] avec le motif, colorier l'arc AB avec la couleur de fond et redessiner le demi-cercle de diamètre [CO].

Télécharger la figure GéoPlan lunule.g2w

Voir : arc de cercle

2.d. Aire sous une voûte

Une voûte est construite sur le segment [OA], avec deux arcs de cercle OI et AI, de centre A et O.

Avec OA = 1, vérifier que l'aire sous la voûte OAI est − .

Deux méthodes

a. On calcule l'aire d'un secteur angulaire ajoutée à une lunule :

Le secteur angulaire OAI, de centre A et d'angle 60°, est ,
l'aire de la lunule déterminée par la corde IA est − ;

l'aire totale est + − = − .

b. On retrouve ce résultat avec l'aire du secteur angulaire OAI, de centre A, ajoutée à l'aire du secteur angulaire AOI, de centre I, auxquelles on retranche , aire du triangle équilatéral OAI comptée deux fois.

3. Cercles et triangle équilatéral

Classe de seconde

3.a. Triangle équilatéral

Construction d'un triangle équilatéral inscrit dans un cercle, avec un deuxième cercle de même rayon

Les cercles (c₁) de centre O₁ et (c₂) de centre O₂ ont même rayon R ; le centre de l'un appartient à l'autre.
Le point C est le symétrique de O₁ par rapport à O₂.
Les deux cercles se coupent en A et B.

  • Montrer que le triangle ABC est équilatéral de côté R .

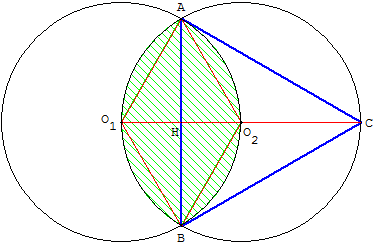
Indications :
les triangles AO₁O₂ et BO₁O₂ sont équilatéraux (configuration d'Euclide).

L'angle au centre AO₂B est égal à 120°. L'angle inscrit ACB mesure 60°.
Le triangle ABC, ayant la droite (CO₁) comme axe de symétrie, est isocèle.
Un triangle isocèle ayant un angle de 60° est équilatéral.

Télécharger la figure GéoPlan tri_2cer.g2w

Voir le cercle circonscrit au triangle équilatéral pour le calcul R de la longueur du côté.

3.b. Périmètre

  • Quels sont le périmètre et l'aire de la surface hachurée formée par les deux segments circulaires (ou lunules) de part et d'autre de la corde [AB] ?

Indications : la surface hachurée est limitée par les deux arcs de cercle AO₁B et AO₂B, arcs de longueur égale.
Sur le cercle (c₂), l'arc AO₁B intercepte l'angle au centre AO₂B de 120°, égal au de 360°.
La longueur de l'arc est donc est égale à du périmètre 2πR du cercle, soit πR.

Le périmètre de la surface hachurée est alors de πR.

3.c. Aire comme réunion de deux segments circulaires

La surface hachurée est la réunion de deux segments circulaires, de même aire, délimités par la corde [AB] et les deux arcs de cercle.
L'aire du segment circulaire AO₁B est égale à l'aire du secteur angulaire AO₂B diminué de l'aire du triangle AO₂B.
L'aire du secteur angulaire AO₂B est égale à de l'aire πR² du cercle, soit πR².
Le point O₂ est le centre du triangle équilatéral ABC, de côté AB = R,
de hauteur HC = R et d'aire AB × HC = R × R = 3R².
Les triangles AO₂B, BO₂C et CO₂A, d'aire égale, partagent le triangle ABC en trois.
L'aire du triangle AO₂B est donc × 3R² soit R².
L'aire du segment circulaire AO₁B est : πR² − R² = ( − )R².
L'aire de la surface hachurée est égale à ( − )R².

3.d. Calcul de l'aire entre les deux cercles

Découpage avec deux triangles équilatéraux et quatre segments circulaires

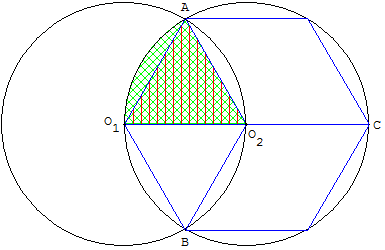
La surface est la réunion des deux triangles équilatéraux AO₁O₂ et BO₁O₂ et quatre segments circulaires O₁A, AO₂, O₁B et BO₂.

Les triangles équilatéraux de côté R et de hauteur h = R
ont pour aire : O₁O₂× h = R × R = R².

Le secteur angulaire O₁O₂A a une aire égale au sixième
de l'aire du cercle (c₂), soit πR².
L'aire du segment circulaire O₁A est égale à l'aire du secteur angulaire moins l'aire du triangle équilatéral, soit πR² − R².

L'aire de la surface totale, comprise entre les deux cercles, est alors 4 (πR² − R²) + 2 R² = ( − )R².

Télécharger la figure GéoPlan 2_lunules.g2w

4. Un partage équitable – Olympiades 2008 de première

Sujets nationaux - Exercice n^o2 (toutes sections)

4.a. Partage en trois parties de même aire

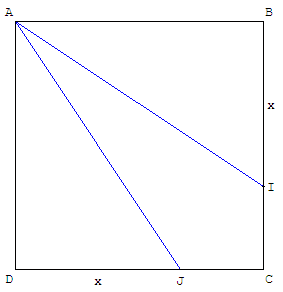
Léonard est géomètre. Il veut partager un carré de côté 1 en trois parties de même aire selon le schéma ci-dessus à gauche.
Quelle valeur doit-il donner à x pour arriver à ses fins ?

L'aire du triangle rectangle de petits côtés 1 et x est x/2.
La solution est x = .

Télécharger la figure GéoPlan carre_olymp.g2w

4.b. Trois triangles

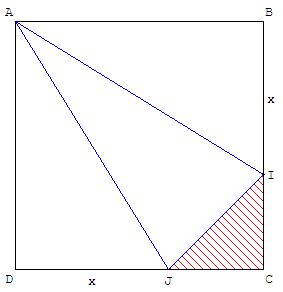
Mais Léonard est aussi esthète. Ne trouvant pas élégante sa construction,il décide de supprimer la zone triangulaire hachurée.
Ainsi, les trois parties restantes sont triangulaires.
Peuvent-elles avoir la même aire ?

L'aire du triangle CIJ est (1 - x)²/2.
D'où l'équation 1 - (1 - x)²/2 = 3 x/2 qui a pour solution positive
l'inverse du nombre d'or x = = .

Télécharger la figure GéoPlancarre_olymp2.g2w

4.c. Point de concours

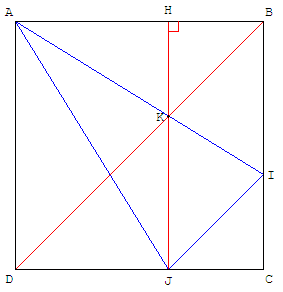
Et Léonard est mathématicien.
Ayant réalisé grossièrement (ci-dessous) la construction de la question 2, il mène du point J la perpendiculaire (IH) à la droite (CD).
Il a l'impression que les droites (JH), (AI) et (BD) sont concourantes. Qu'en est-il ?

Dans le repère (D, , ) le point K d'intersection des droites (JH) et (BD) a pour coordonnées (, ).

Vérifier que ces coordonnées satisfont à l'équation de la droite (AI) : y - 1 = - x.

Télécharger la figure GéoPlancarre_olymp3.g2w