Descartes et les Mathématiques
Géométrie en cinquième
Programme de géométrie en classe de cinquième : construction de triangles avec un logiciel de géométrie dynamique.
Sommaire
I Construction de triangles
1. Deux droites
2. Construire un triangle connaissant les trois côtés
3. Construire un triangle connaissant deux côtés et l'angle compris entre ces deux côtés
4. Construire un triangle connaissant un côté et deux angles adjacents
5. Triangles isocèles ayant un angle de 80 degrés
6. Cerfs-volants inscrits dans deux cercles sécants
II Calcul d'aires
2.1. Goutte d'eau
2.2. Entre deux cercles - Une fleur de quatre pétales
2.3. Un triangle inscrit dans un rectangle
2.4. Un triangle inscrit dans un carré
Quelques exercices où l'on regrette l'abandon des « cas d'égalité des triangles » qui fournissent un fondement de la géométrie, imparfait certes, mais sur lesquels les autres résultats reposaient solidement.
(D'après : quelques réflexions sur la géométrie et son enseignement - Daniel Perrin - Bulletin APMEP no 480 janvier-février 2009
Voir aussi : quels contenus pour l'enseignement)
Les problèmes de géométrie proposés dans les pages « Descartes et les Mathématiques » sont assez guidés. À partir d'exercices, souvent proposés en classe, nous avons abrégé la démarche expérimentale et, en raison de la nature du média Internet, nous livrons telles quelles des indications. Ceci est, en général, suffisant pour les élèves qui auront à s'approprier les solutions et à rédiger les démonstrations.
Les professeurs voulant utiliser ces activités en classe devront reconstituer la démarche pédagogique. Par exemple, la question « démontrer que les droites (AB) et (CD) sont parallèles » pourra être à remplacée par « que peut-on dire des droites (AB) et (CD) » ou encore de façon plus elliptique par « que peut-on dire », quitte à affronter le rigolo du fond de la classe qui répondra « rien ».
1. Deux droites
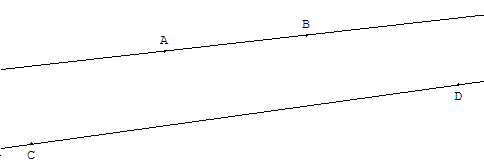
Que dire des deux droites ci-dessus ?
Avec GéoPlan, changer le cadrage en tapant sur la touche agrandir (>).
Modifier la droite (CD) en tapant sur la touche P.
Que dit alors GéoPlan, à propos de l'intersection des droites (AB) et (CD) ?
Indications : sécantes ou non ?
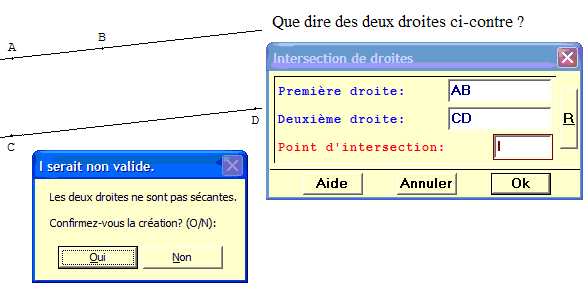
Les deux droites ci-dessus semblent parallèles, mais GéoPlan accepte de tracer leur point d'intersection.
Vérifions avec un agrandissement où en déplaçant la vue (clic droit maintenu avec GéoPlan).
Par la touche P, l'affectation directe du point D permet de tracer une droite (CD) parallèle à (AB).
GéoPlan renâcle alors à créer le point d'intersection.
Télécharger la figure GéoPlan deux_droites.g2w
Résolution de triangles
2. Tracer un triangle connaissant les trois côtés
Inégalité triangulaire
Programme de cinquième
Connaître et utiliser l'inégalité triangulaire pour construire un triangle connaissant les longueurs des trois côtés.
Lorsque la construction est possible, les élèves sont invités à remarquer que lorsqu'un côté est tracé, on peut construire plusieurs triangles, deux à deux symétriques par rapport à ce côté, à sa médiatrice et à son milieu.
L'inégalité triangulaire est mise en évidence à cette occasion et son énoncé est admis :
AB + BC ≥ AC.
Le cas de l'égalité AB + BC = AC est reconnu comme caractéristique de l'appartenance du point B au segment [AC].
Ces constructions permettent un premier contact (implicite) avec les trois cas d'isométrie des triangles (théorèmes rencontrés en classe de 2nde).
Comment dessiner un triangle
Construire un triangle de côtés donnés
Dessiner un triangle connaissant les longueurs des trois côtés
Étant donné un segment [BC] de longueur a et deux nombres positifs b et c, construire un triangle ABC tel que AC = b et AB = c
Tracer les cercles (c1) de centre B, de rayon c et (c2) de centre C de rayon b.
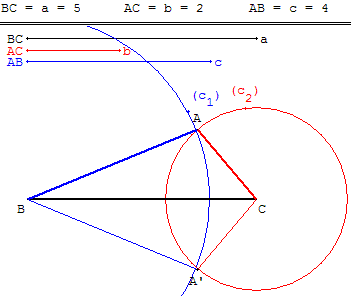
Deux triangles
Si les cercles (c1) et (c2) sont sécants en deux points distincts A et A’, le triangle ABC est une construction possible, le triangle A’BC est aussi une solution. Ces deux triangles sont symétriques par rapport à la droite (BC).
Dans ce cas a + b ≥ c, l'inégalité triangulaire BA + AC ≥ BC est vérifiée.
Télécharger la figure GéoPlan tri_cotes_donnes.g2w
Quatre triangles
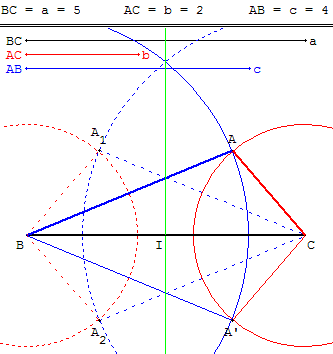
Lorsqu'il y a une solution, si les longueurs sont distinctes, on peut construire quatre triangles, deux à deux symétriques par rapport au côté [BC], à sa médiatrice et à son milieu.
Télécharger la figure GéoPlan tri_cotes_donnes2.g2w
Commandes GéoPlan
Faire varier les longueurs BC, AB ou CA, en déplaçant les extrémités a, b ou c.
BC trop grand
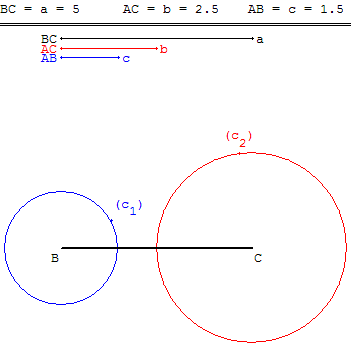
Si b + c < a les cercles (c1) et (c2) sont extérieurs l'un à l'autre, la construction est impossible.
Si b + c = a les deux cercles sont tangents en A (confondu avec A’), l'égalité BA + AC = BC caractérise l'appartenance du point A au segment [BC].
BC trop petit
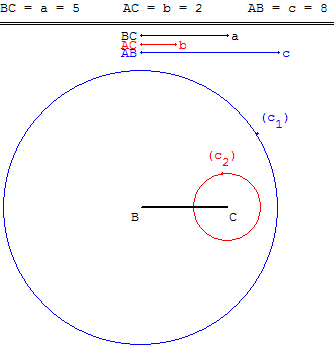
Si a + b < c ou a + c < b un des cercles (c1) ou (c2) est à l'intérieur de l'autre, la construction est impossible.
Si a + b = c ou a + c = b les deux cercles sont tangents intérieurement en A (confondu avec A’), le point A est sur la droite (BC).
Image dupliquée dans un des cercles à l'intérieur de l'autre
3. Construire un triangle avec deux côtés et un angle
Tracer un triangle connaissant les longueurs de deux côtés et l'angle compris entre ces deux côtés
Étant donné un segment [AB] de longueur c, un nombre positif b et un angle xÔy,
tracer un triangle ABC tel que AC = b et que BÂC = xÔy.
Pour reporter l'angle xÔy sur la demi-droite [AB), on trace les cercles (c1) et (c2) de centres O et A et de rayon c. [Ox)
rencontre (c1) en M et [Oy) en P.
Avec le compas, on reporte l'arc MP, en traçant le cercle (c3) de centre B et de rayon MP. Ce cercle coupe (c2) en Q et Q’. Les angles BÂQ et BÂQ’ sont égaux à xÔy.
[AQ) rencontre le cercle (c4) de centre A et de rayon b en C et [AQ’) en C’.
Le triangle ABC est une construction toujours possible (b > 0, c > 0 et 0 < xÔy < 180°), le triangle ABC’ est aussi une solution. Ces deux triangles sont symétriques par rapport à la droite (AB).
Si ABC n'est pas un triangle isocèle en C, en reportant l'angle xÔy en B sur la demi-droite [BA) on obtient deux autres triangles symétriques du triangle ABC par rapport au milieu de [AB] et à sa médiatrice.
Commandes GéoPlan
Faire varier les longueurs des côtés en cliquant sur b ou c ou l'angle en déplaçant les points x ou y.
La figure est plus lisible lorsque b < c, renommer éventuellement les points.
Télécharger la figure GéoPlan tri_2cotes_1angle.g2w
Voir aussi : construire un triangle connaissant un angle, un côté adjacent et la somme des deux autres
4. Construire un triangle avec un côté et deux angles
Tracer un triangle connaissant la longueur d'un côté et les deux angles qui lui sont adjacents
Étant donné un segment [AB] de longueur c, deux angles xÎy et zJt,
dessiner un triangle ABC tel que BÂC = xÎy et ABC = zJt.
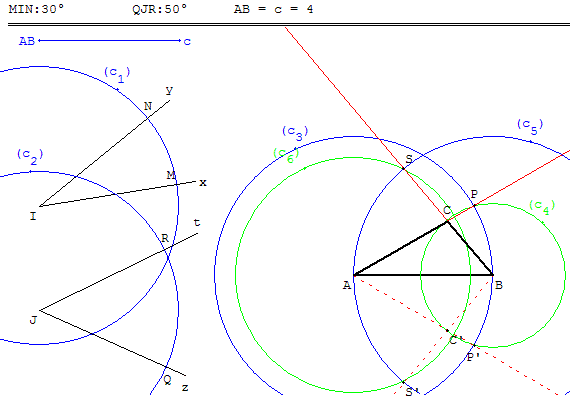
Pour reporter l'angle xÎy sur la demi-droite [AB) on trace les cercles (c1) et (c3) de centres I et A et de rayon c.
[Ix) rencontre (c1) en M et [Iy) en N.
Avec le compas, on reporte l'arc MN, en traçant le cercle (c4) de centre B et de rayon MN. Ce cercle coupe (c2) en P et P’.
Les angles BÂP et BÂP’ sont égaux à xÎy.
De même, pour reporter l'angle zJt sur la demi-droite [BA) on trace les cercles (c2) et (c5) et centres J et B et de rayon c.
On reporte l'arc QR, en traçant le cercle (c6) de centre A et de rayon QR.
Ce cercle coupe (c5) en S et S’. Les angles ABS et ABS’ sont égaux à zJt.
Si les demi-droites [AP) et [BS) sont sécantes en un point C, le triangle ABC est une construction possible. Les demi-droites [AP’) et [BS’) sont alors sécantes en C’, le triangle ABC’ est aussi une solution. Ces deux triangles sont symétriques par rapport à la droite (AB).
Si ABC n'est pas un triangle isocèle en C, en permutant les angles on obtient deux autres triangles symétriques du triangle ABC par rapport au milieu de [AB] et à sa médiatrice.
La somme des angles d'un triangle étant un angle plat :
+ 
+ 
= 180°,
la construction est possible lorsque + < 180°,
soit xÎy + zJt < 180°.
Télécharger la figure GéoPlan tri_2cotes_1angle.g2w
Commandes GéoPlan
Faire varier la longueur de [AB]
ou les angles en déplaçant les points x, y, z ou t,
Figure copiée dans construire un triangle connaissant un côté et deux angles
5. Triangles isocèles ayant un angle de 80 degrés
5.a.Triangle isocèle avec un angle au sommet de 80°
Report d'angle et construction du triangle isocèle avec un cercle de centre A.
Étant donné une longueur c et un angle xÔy, construire un triangle isocèle ABC tel que AB = AC = c et que BÂC = xÔy.
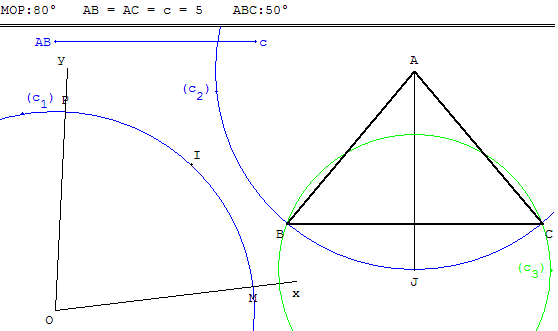
En adaptant la construction du paragraphe 3, reporter la moitié de l'angle xÔy sur une demi-droite [AJ) passant par A.
On trace les cercles (c1) et (c2) de centres O et A et de rayon c. [Ox) rencontre (c1) en M et [Oy) en P.
La bissectrice de MÔP coupe le cercle (c1) en I qui partage l'arc MP en deux parties égales. Avec le compas, on reporte l'arc IM, en traçant le cercle (c3) de centre J et de rayon IM. Ce cercle coupe (c2) en B et C’.
L'angle BÂC est égal à xÔy.
La construction du triangle isocèle ABC est toujours possible.
Comme la somme des angles d'un triangle est 180°,
avec =
on a + 2 =180° et en divisant par 2 : = 90 − 
.
Télécharger la figure GéoPlan tri_iso.g2w
Commandes GéoPlan
Faire varier les longueurs des côtés égaux,
ou l'angle en déplaçant x ou y.
5.b. Tracer un triangle isocèle ayant deux angles de 80°
Étant donné une longueur a et un angle xÔy de 80 degrés, construire un triangle ABC isocèle en A
tel que la base BC = a et que ABC = xÔy.
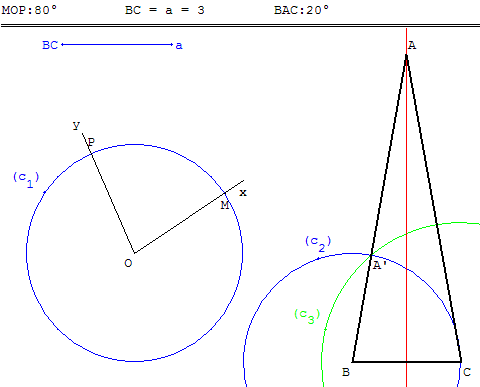
Pour reporter l'angle xÔy sur la demi-droite [BC) on trace les cercles (c1) et (c2) de centres O et B et de rayon a. [Ox) rencontre (c1) en M et [Oy) en P. Avec le compas, on reporte l'arc MP, en traçant le cercle (c3) de centre C et de rayon MP. Ce cercle coupe (c2) en A’ et l'angle A’BC est égal à xÔy.
Si la demi-droite [AA’) coupe la médiatrice de [BC], le point d'intersection A est le sommet du triangle isocèle ABC.
Cette construction n'est possible que si xÔy <90° (les angles égaux d'un triangle isocèle sont aigus).
Comme la somme des angles d'un triangle est 180°, avec = ,
on a + 2 =180° et = 180° −2 .
Commandes GéoPlan
Faire varier la longueur de la base.,
ou l'angle en déplaçant x ou y.
Télécharger la figure GéoPlan tri_iso2.g2w
6. Cerfs-volants inscrits dans deux cercles
Figures simples ayant un centre de symétrie ou des axes de symétrie.
Cerfs-volants (géométrie) dans deux cercles sécants
Deux cercles (c) et (c’) de centres distincts O et O’sont sécants en A et B.
La ligne des centres (OO’) coupe (c) en C et (c’) en D.
La droite (OO’) est la médiatrice de [AB] et est axe de symétrie de la figure.
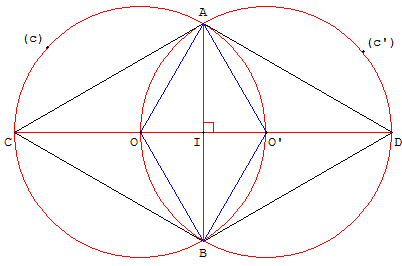
Cercles de même rayon : chacun des cercles passe par le centre de l'autre
Les droites (OO’) et (AB) sont deux axes de symétrie et leur point d'intersection I est centre de symétrie de la figure.
Les quadrilatères AOBO’ et ACBD sont des losanges d'angles 60° et 120°.
Télécharger la figure GéoPlan deux_cercles_egaux.g2w
Voir : cercles et triangle équilatéral
Image copiée dans pintetest : cerfs-volants inscrits dans 2 cercles ou deux losanges
Cas général : cercles de rayons différents
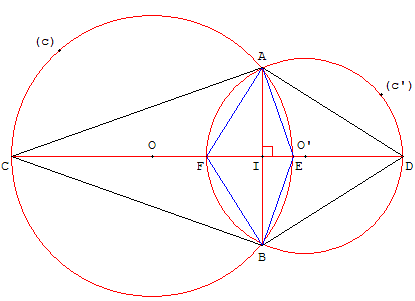
La ligne des centres (OO’) coupe le cercle (c) en C et E, et le cercle (c’) en D et F.
Les quadrilatères ACBD et AEBF sont des cerfs-volants, ainsi que ACBE et AFBD.
Remarquer aussi les pointes de flèche ACBF et ADBE.
Télécharger la figure GéoPlan deux_cercles.g2w
II. Reproduction de figures
2.1. Goutte d'eau
A, B et C sont trois points alignés tels que : AB = 4 cm, BC = 6 cm.
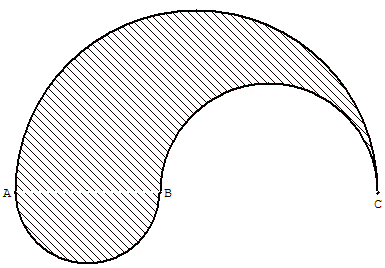
Cette figure est formée de trois demi-cercles.
– Calculer son périmètre.
– Calculer son aire.
Télécharger la figure GéoPlan goutte_eau.g2w
2.2.a. Entre deux cercles
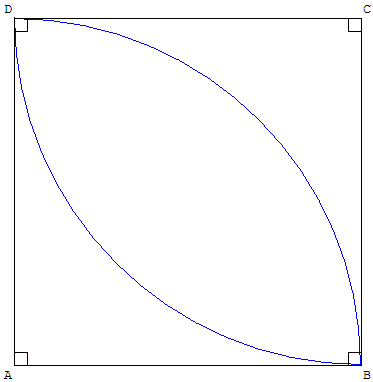
ABCD est un carré de 1 cm de côté.
Calculer l'aire de la figure délimitée par les arcs de cercle, de centres A et C, passant par B et D.
Télécharger la figure GéoPlan aire_entre_2_cercles.g2w
2.2.b. Une fleur de quatre pétales
Fleur du comportement
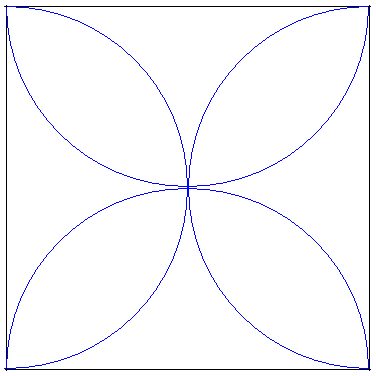
Dans un carré de 2 cm de côté, les quatre pétales sont formés par l'intersection de demi-cercles.
Calculer l'aire de la fleur formée par les quatre pétales.
Télécharger la figure GéoPlan fleur.g2w
Aire d'un triangle inscrit
2.3. Un triangle dans un rectangle ou un carré
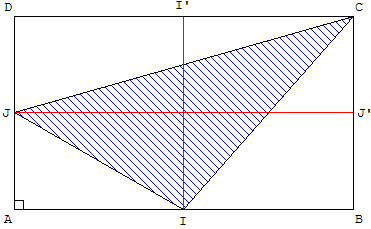
I, I’ et J, J’ sont les milieux des côtés d'un rectangle ABCD de centre O.
Un triangle est inscrit dans un rectangle de côtés de longueurs AB = 6 cm
et de largeur BC = 3 cm sur la figure de gauche,
sur la figure-ci-dessous, un triangle est inscrit dans un carré de côté AB = 4 cm.
Quelle fraction de l'aire du quadrilatère ABCD représente l'aire du triangle CIJ ?
Pour cela, calculer quelles fractions de l'aire du quadrilatère représente l'aire de chacun des triangles AIJ, BIC et DCJ.
Indications
Aire(BIC) = 
Aire(BII’C) = 
Aire(ABCD) ; Aire(DCJ) = Aire(DCJ’J) = Aire(ABCD) ;
Aire(AIJ) = Aire(AIOJ) = 
Aire(ABCD),
Aire(BIC) + Aire(DCJ) + Aire(DCJ) = ( + + )Aire(ABCD) = 
Aire(ABCD),
Aire(CIJ) = Aire(ABCD) - [Aire(BIC) + Aire(DCJ) + Aire(DCJ)] = 
Aire(ABCD).
Télécharger les figures GéoPlan triangle_ds_rectangle.g2w,
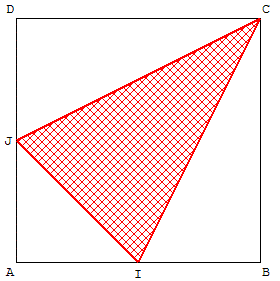
2.4. Aire d'un triangle dans un carré
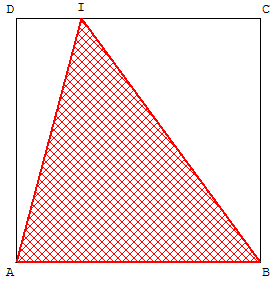
I est un point du côté [CD] d'un carré ABCD, de longueur AB = 4 cm.
ABI est un triangle inscrit dans le carré.
Quelle fraction de l'aire du carré représente l'aire du triangle ABI ?
Réponse
L'aire du triangle ABI est la moitié de l'aire du carré, soit 8 cm2.
Télécharger la figure GéoPlan triangle_ds_carre_g2w
Contribution de Ressources numériques sélectionnées pour le scénario du carip
4ème ressource : la ressource est fiable puisqu'elle est extraite de la section mathématiques du site de l'académie d'Aix-Marseille.
Ce que nous allons retenir pour notre scénario: La particularité de l'exercice qui fait intervenir deux figures (carré et triangle) ont une relation entre leurs aires.
Exercice qui va plus loin qu'un simple calcul d'aire de niveau 6ème.
Ce que nous modifierons: Il nous semble plus judicieux de ne pas mettre de longeur pour introduire un niveau de généralisation plus élevé.
De plus, sans valeur numérique les élèves seront plus tentés par une résolution littérale, un de nos objectif.
Table des matières
Liens vers d'autres pages du site
Médiatrices : géométrie du triangle
Hauteurs : géométrie du triangle
Somme des angles d'un triangle : triangle au collège
Construction du triangle équilatéral
Symétrique d'un point par rapport à un autre : construction au compas seul
Constructions avec contraintes - Reproduction de figures
Carré et triangles équilatéraux alignement de trois points
Exercice collège angle inconnu
Calcul d'aires au collège :
Aire du parallélogramme, du trapèze, du triangle, aire et médiane.
Deux parallélogrammes d'aires égales
Partage d'un parallélogramme en deux polygones croisés
– Tracer le symétrique d'un triangle
– Construction, à la règle et l'équerre, d'une perpendiculaire ou d'un carré passant par un point inaccessible
Recherche de geometrie pour le plaisir avec programme de construction
Téléchargement des anciennes versions de 2008
Télécharger geometrie_cinquieme.doc : ce document au format « .doc »
Télécharger geometrie_cinquieme.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image et ne devrait pas être référencée comme tel par Google !
Google considère l'URL comme une erreur de type "soft 404"!
Google friendly
|
|
Page no 95, réalisée le 9/10/2006 |