René Descartes Descartes et les Mathématiques

Constructions au compas seul

Sommaire

1. Bissectrice d'un angle

2. Parallèle à une droite passant par un point donné

3. Symétrique d'un point par rapport à un autre

4. Symétrique d'un point par rapport à une droite

5. Angle droit

6. Milieu d'un segment

7. Problème de Napoléonien

Autres constructions au compas seul

Comment tracer la médiatrice d'un segment avec un compas :
– Construction de la médiatrice au compas

– GeoGebraTube : construction de la médiatrice

Comment tracer les hauteurs d'un triangle avec un compas

Tracer un parallélogramme à partir de trois sommets

Constructions de tangentes à un cercle

Triangle équilatéral

Hexagone régulier

Humeur et tableau noir – Plot n^o 25

Le théorème de Mohr-Mascheroni, montré par Georg Mohr, puis par Lorenzo Mancheron en 1797, affirme que si une construction géométrique est possible à la « règle et au compas », alors elle est possible au compas seul.

1. Bissectrice d'un angle

Les figures n'ont pas encore été transférées de l'ancien site Orange

construction au compas seul - bissectrice d'un angle - copyright Patrice Debart 2007

GéoPlan permet de tracer une bissectrice à partir d'un angle défini par trois points.
Pour tracer une bissectrice « à la règle et au compas » on se place dans la situation d'un triangle isocèle OAB que l'on complète par un point I tel que le quadrilatère BOAI soit un losange.

Soit un angle de sommet O formé par deux demi-droites (d₁) et (d₂) ayant ce point pour origine. Placer un point A sur un des côtés (d₁) de l'angle.
Tracer le cercle de centre O, passant par A, qui coupe la deuxième demi-droite (d₂) en B.
Tracer les deux cercles de centre A et B passant par O. Ces deux cercles se recoupent en I.

[OI) est la bissectrice intérieure de l'angle des demi-droites (d₁) et (d₂) :

La diagonale (OI) du losange OABI, est la médiatrice de [AB] car les diagonales du losange se coupent en H milieu de [AB] et sont perpendiculaires.
Dans le triangle isocèle OAB, les angles AÔH et HÔB sont égaux, la droite (OI) est donc la bissectrice, issue de O, de ce triangle.

Voir : construction avec la règle à bords parallèles

2. Trace la parallèle à une droite passant par un point

Méthode des angles alternes-internes

Paragraphe extrait de l'article parallèle à une droite passant par un point donné

construction au compas seul - parallele à une droite - copyright Patrice Debart 2007

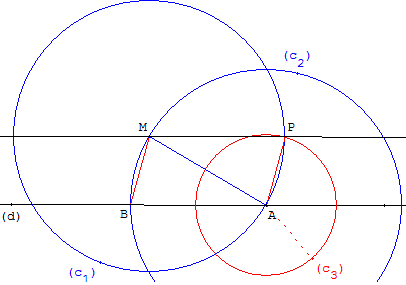
Soit une droite (d), A et B deux points sur (d) et un point M à l'extérieur de (d).

Une droite (d’) est la parallèle à (d), passant par le point M, si la sécante (AM) fait, avec les droites (d) et (d’), des angles alternes-internes, BMA et MAP, égaux entre eux.

Pour cela :

Tracer le cercle (c₁) de centre M passant par le point A de la droite (d), puis le cercle (c₂) de centre A passant par M. Le cercle (c₂) coupe la droite (d) en B.

Pour reporter l'angle BMA en A, reporter l'arc MB de (c₂) sur le cercle (c₁). Tracer le cercle (c₃) de centre A et de rayon BM.
Choisir pour P, le point d'intersection des cercles (c₁) et (c₃) situé du même côté que A par rapport à (d).

Les triangles BMA et PAM ont leurs côtés deux à deux de même longueur. Ils sont isométriques : les angles BMA et MAP ont même mesure : la droite (MP) est la parallèle à (d), passant par M, cherchée.

Télécharger la figure GéoPlan parallele_5.g2w

3. Symétrique d'un point par rapport à un autre point

Classe de cinquième

construction au compas seul - symetrique d'un point - copyright Patrice Debart 2007

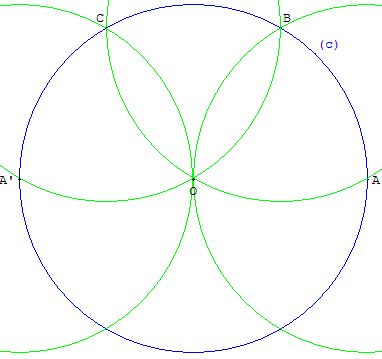
Pour construire le symétrique d'un point A par rapport à un point O, il suffit de tracer successivement trois triangles équilatéraux OAB, OBC, OCA’ à partir du segment [AO].

Le cercle de centre A passant par O coupe le cercle (c) en B et F,
le cercle de centre B passant par O recoupe le cercle (c) en C,
le cercle de centre C passant par O coupe le cercle (c) en A’.

Le point A’ est le symétrique de A par la symétrie de centre O.

Télécharger la figure GéoPlan point_sym_centrale.g2w

4. Symétrique d'un point par rapport à une droite

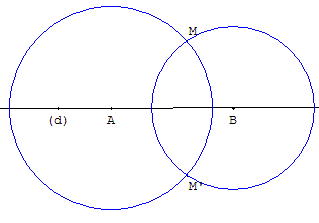
Le symétrique d'un point M par rapport à une droite (AB) se construit en traçant les deux cercles de centrés sur la droite en A et B et passant par M.

Le point M’, deuxième point d'intersection des deux cercles, est le symétrique de M.

5. Angle droit

construction au compas seul - angle droit - copyright Patrice Debart 2007

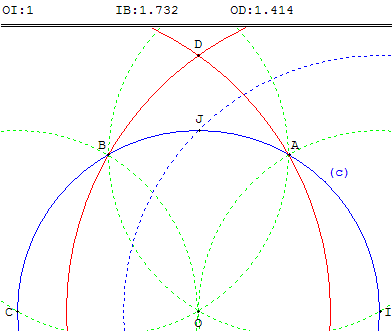
À partir de deux points O et I, pour tracer un angle droit IÔJ, tracer comme ci-dessus le cercle (c) de centre O, passant par I, et le symétrique C de I, par rapport à O.

Le triangle IAC est un triangle rectangle en A, ayant un angle AÎC = .
Donc, CA = CI = OI et IB = CA.

Les cercles de rayon OI centrés en I et C passant par B et A se coupent en D.

La propriété de Pythagore dans le triangle IOD permet de calculer OD ;

OD² = ID² - OI² = 3 OI² - OI² = 2 OI² et OD = OI.

OD est la longueur du côté du carré inscrit dans le cercle (c).

Le point J cherché est une des intersections du cercle (c) avec le cercle de centre I et de rayon OD.

6. Milieu d'un segment

Le milieu I d'un segment [AB] est constructible au compas seul.

Figure de base

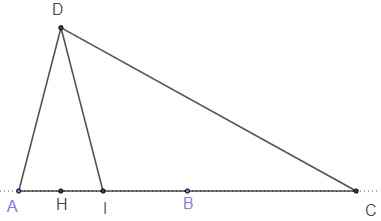
Le principe consiste à utiliser les propriétés de la figure ci-dessus dans laquelle le segment [AB] a pour longueur1.
Le point C est le symétrique de A par rapport à B, . C est constructible d'après le paragraphe 3.
les segments [AC] et [CD] ont pour longueur 2 et les segments [AD] et [DI] ont pour longueur 1.
Les triangles ACD et ADI sont semblables car ils sont tous les deux isocèles et partagent un même sommet de base DAI.
Le segment [AI] a donc pour longueur AI = AD = et le point I est le milieu du segment [AB].
Il suffit de reproduire les points de cette figure uniquement au compas.

Construction

Les cercles de centre A passant par B et de centre C passant par A se coupent en D et D’.
Les cercles de centres D et D’ passant par A se recoupent en I milieu du segment [AB].

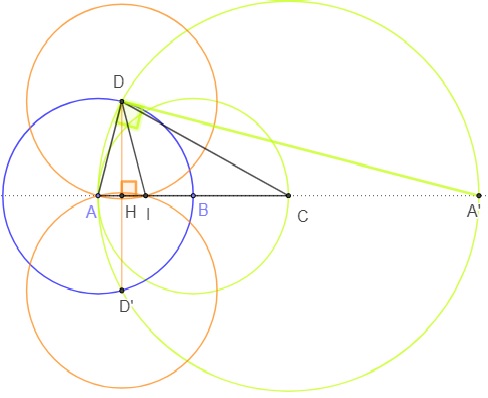
Preuve

En effet, soit A’ le symétrique de A par rapport à C et H l'intersection de (AB) et (DD’).

Comme H est le pied de la hauteur du triangle rectangle ADA’ inscrit dans le demi-cercle de centre C, on a :
AD² = AH × AA’, soit AD² = AH × 4 AB.

On obtient donc AH = et ainsi AI = .

Figure interactive dans GeoGebraTube : Milieu d'un segment

Constructions du milieu d'un segment

Voir : construction du milieu avec une règle à bords parallèles

7. Problème de Napoléon : retrouver le centre d'un cercle

Sans doute savez-vous facilement retrouver le centre d'un cercle avec une règle et un compas… et oui tracer une médiatrice demande un compas !

Hilbert a montré que l'on ne pouvait pas le retrouver avec seulement une règle.

Pour le retrouver avec uniquement un compas, c'est en 1797 que l'on voit apparaître Napoléon. Même pour les mathématiques l'empereur, c'est une légende :
Sur une plage de l'île de beauté, Napoléon, équipé d'un simple compas (à défaut d'épuisette), traça un cercle (d'un trait continu). Quand il revint quelques minutes plus tard, le centre avait disparu. Sans s'émouvoir, et bien qu'ayant perdu l'ouverture du compas qui lui avait permis de tracer le cercle, l'empereur retrouva son centre, sous le regard admiratif de son entourage. Est-ce à ce propos que Lagrange aurait dit : « Mon Général, nous nous attendions à tout de vous, sauf à des leçons de géométrie » ?
Autre version moins romantique : lors de la campagne d'Italie, il rencontra Mancheron, spécialiste de la géométrie du compas. De retour en France, il exposa à l'Académie des Sciences les résultats de ce mathématicien, ainsi qu'une solution personnelle de ce problème trouvée avec son aide.

A et B sont deux points sur le cercle initial (c).

trouver le centre d'un cercle avec un compas - copyright Patrice Debart 2007

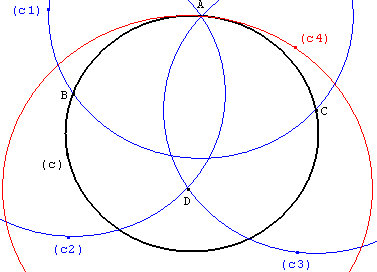
Étape 1 : tracer le cercle (c₁) de centre A passant par B. Ce cercle coupe aussi (c) en C. Tracer les cercles (c₂) et (c₃) de centres B et C passant par A. Ces deux derniers cercles se recoupent en D.
Étape 2 : tracer le cercle (c₄) de centre D passant par A.

Étape 3 : le cercle (c₄) coupe (c₁) en E et F.

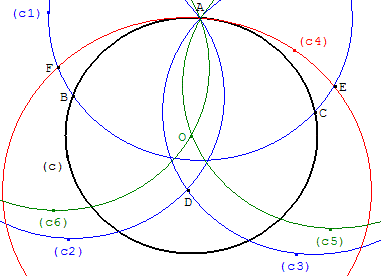
Les cercles (c₅) et (c₆) de centres E et F passant par A se recoupent en O, centre du cercle (c).

Avec GéoPlan, charger la figure : taper 3, puis 2 et 1 pour effacer les constructions ; taper 1, puis 2 et 3 pour voir les trois étapes de la solution.

Démonstration d'après Napoléon

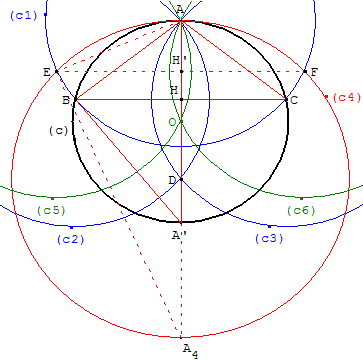
Soit r, r₁ et r₄ les rayons des cercles (c), (c₁) et (c₄). ABDC est un losange de longueur de côté r₁. La droite (AD), médiatrice de [BC], contient le centre du cercle (c), le milieu H du losange et A’ point diamétralement opposé à A sur le cercle (c).

Dans le cercle (c), ACB et AÂ’B sont deux angles inscrits égaux interceptant l'arc AB. Les triangles rectangles AHC et ABC’ ayant même angle aigu sont semblables :
sin(HCA) = AH/AC = (DA/2)/AC = DA/ (2r₁).
sin(AÂ’B) = AB/AA’ = r₁/(2r).
Donc, DA/(2r₁) = r₁/(2r) soit r₄ = DA = r₁²/r.

Un calcul similaire avec le cercle (c₄) et les points A, E, F et O permet de montrer que OA = r₁²/r₄.
En simplifiant OA = r₁²/(r₁²/r), on trouve OA = r. Le point O situé sur (AD) à une distance r de A est bien le centre du cercle (c).