Descartes et les Mathématiques
Construction avec une équerre
Perpendiculaire, médiatrice, parallèles, parallélogramme, losange, carré.
Sommaire
3. Deux parallèles : angles alternes-internes, angles correspondants
4. Une parallèle avec une équerre glissant sur une règle
5. Un parallélogramme, le milieu d'un segment
6. Une médiatrice : règle graduée et équerre
7. Un losange, une médiatrice uniquement à l'équerre
8. Un carré
9. À la recherche du centre perdu
Les constructions à l'équerre sont assez imprécises.
Elles font toutefois partie de l'apprentissage normal des élèves de 9 à 13 ans.
Bien qu'ensuite on préférera les constructions à la règle au compas,
certaines constructions à l'équerre ne manquent pas de piment,
entre autres en utilisant un angle aigu de cet instrument
comme « gabarit d'angle ».
Les figures sont dynamiques et il est possible
de déplacer les points de base et les équerres.
Pour la lisibilité des figures, la taille des équerres a été minorée.
On peut la régler avec le paramètre l, qui représente la longueur
de l'hypoténuse. t est la mesure d'un des angles aigus de l'équerre, en radians.
On utilise, le plus souvent, deux types d'équerre :
– le « demi-carré » : triangle rectangle isocèle
d'angles aigus de 45° (t = 
radians),
de côtés (1, 1, 
).
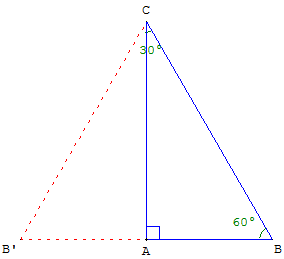
– le « triangle de l'écolier » : demi-triangle équilatéral
avec des angles aigus de 30° et 60° (t = 
ou t = 
).
1. Tracer une perpendiculaire
Avec une équerre, on trace un angle droit
qui permet de dessiner une perpendiculaire.
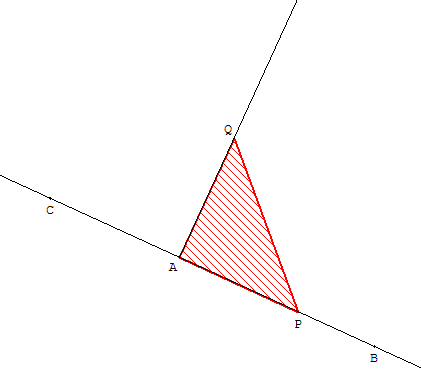
Perpendiculaire à la droite [BC], élevée en A
Construction à l'équerre
Placer l'angle droit de l'équerre en A.
Perpendiculaire abaissée de A sur la droite [BC]
Construction à la règle et l'équerre
Placer un des petits côtés [HP] de l'équerre le long de la droite [BC]
et la faire glisser jusqu'à ce que la perpendiculaire (HQ) passe par le point A.
2. Construire deux parallèles
Tracer une droite parallèle à une droite donnée passant par un point extérieur.
Savoir :
si deux droites sont perpendiculaires à une même
troisième, alors elles sont parallèles.
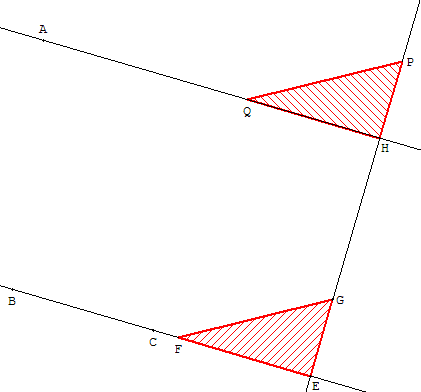
Tracer la parallèle à la droite (BC) passant par un point A extérieur
En sixième, deux droites parallèles sont définies comme deux
droites non sécantes et caractérisées par le fait que si l'une est
perpendiculaire à une troisième droite, l'autre l'est également.
En faisant glisser une équerre le long d'une droite, on trace des parallèles.
Construction :
Placer un des petits côtés [EF] de l'équerre le long de
la droite (AB) et tracer (EG) perpendiculaire à (AB).
Faire glisser l'équerre le long d'une règle bordant (EG)
jusqu'à ce que la perpendiculaire (HQ) passe par A.
Les droites (AH) et (BC), perpendiculaires à (EG), sont parallèles.
3. Construire deux parallèles
Angles alternes-internes, angles correspondants
Tracer une droite parallèle à une droite donnée passant par
un point extérieur avec une règle et «l'angle aigu » d'une équerre.
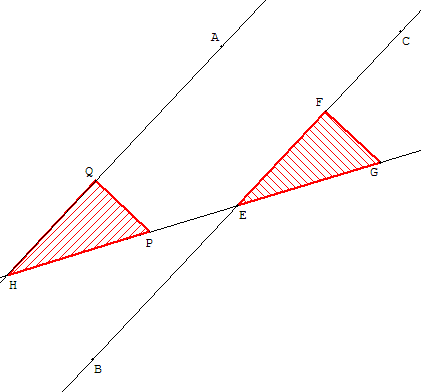
Grâce à la propriété : « deux droites parallèles découpent sur
une sécante des angles alternes internes, alternes externes
ou correspondants de même mesure », on peut utiliser un des
angles aigus de l'équerre comme « gabarit d'angle », en faisant
glisser l'hypoténuse de l'équerre le long d'une règle.
Tracer la parallèle à une droite (BC) passant par un point A extérieur
Construction à la règle et l'équerre
Deux droites parallèles découpent sur une sécante (EG)
des angles correspondants de même mesure.
Placer un des petits côtés [EF] de l'équerre le long
de la droite (BC), et tracer la sécante (EG).
Faire glisser cette équerre le long d'une règle, bordant (EG),
jusqu'au point H, de telle façon que (HQ) passe par A.
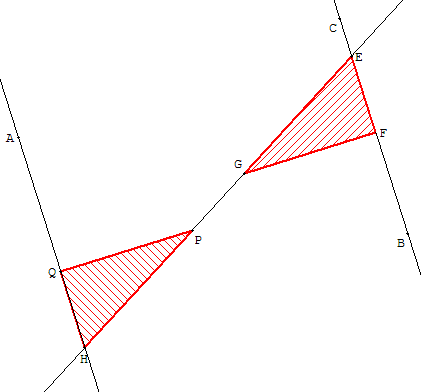
Deux droites parallèles découpent sur une sécante (EG)
des angles alternes-internes de même mesure.
Placer un des petits côtés [EF] de l'équerre le long de la droite (BC),
et tracer la sécante (EG).
Retourner l'équerre et faire glisser cette équerre le long d'une
règle, bordant (EG), jusqu'au point H, de telle façon que (HQ) passe par A.
4. Une parallèle avec équerre sur une règle
Construction, avec une équerre glissant sur une règle,
de la parallèle à une droite (BC), menée à partir d'un point M donné.
Utilisation « dynamique » d'une équerre glissant
sur une règle,de bord (BC), pour construire une parallèle.
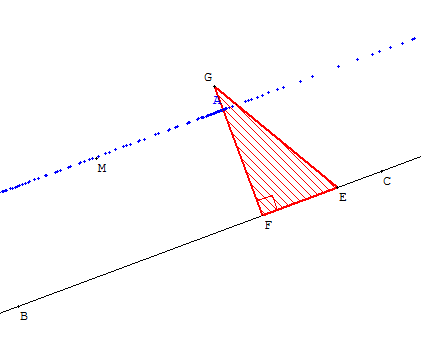
Avec papier crayon, au départ les élèves repèrent un point A
sur l'équerre qui coïncide avec le point M.
Ensuite, ils font glisser l'équerre le long de la règle et tracent
différents points A1, A2, A3… à partir du point A marqué sur l'équerre.
Ils constatent que les points A1, A2, A3… sont alignés avec le point M
et qu'ils déterminent la droite parallèle à (BC), passant par le point M.
Indication
Les distances des traces de A à la droite
sont égales à la distance de M à la droite.
Ces points sont donc alignés sur la parallèle
à la droite (BC) passant par M.
5. Un parallélogramme, le milieu d'un segment
Trouver le milieu d'un segment avec une équerre
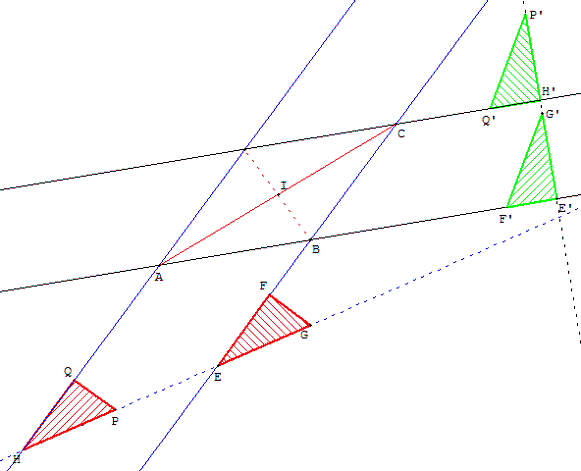
Tracer le milieu de [AC] :
Pour cela, construire un parallélogramme de diagonale
[AC] en plaçant convenablement un point B.
Comme à la règle et à l'équerre, on sait tracer des couples de
parallèles, on sait donc dessiner le quatrième sommet de ce
parallélogramme de sommets A, B et C.
Le point d'intersection des diagonales détermine le milieu.
On peut donc trouver le milieu d'un segment uniquement
à la règle et à l'équerre.
6. Tracer une médiatrice
Définition :
la médiatrice d'un segment [AB] est l'ensemble des points M
du plan équidistants de A et B.
C'est une droite perpendiculaire à (AB) au milieu I de [AB].
La médiatrice est l'axe de symétrie du segment.
6.1 Construction de la médiatrice
Par pliage d'une feuille
Par pliage d'une feuille rabattre un point A sur un point B :
appuyer le pli de la feuille qui marque la médiatrice de [AB].
Règle graduée et équerre
Apprentissage de base :
Avec la règle, mesurer le segment et pointer le milieu I du segment [AB].
Placer l'angle droit l'équerre au milieu, en appuyant
un des petits bords de l'équerre le long du segment.
Tracer la perpendiculaire (IQ), passant par le milieu I,
qui est la médiatrice de [AB].
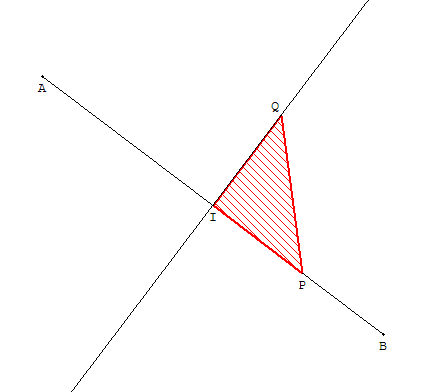
6.2. Dessiner une médiatrice avec compas et équerre
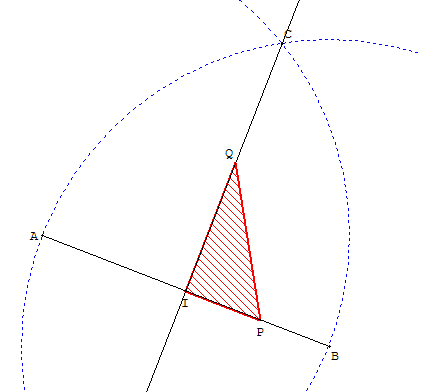
Tracer les cercles de centre A passant par et de centre B passant par A.
Soit C un des points d'intersection de ces deux cercles.
ABC est un triangle équilatéral ayant AB comme longueur des côtés.
Le point C, équidistant de A et B, est un point de la médiatrice de [AB].
Il suffit de tracer la perpendiculaire à (AB) passant par C.
C'est la droite (IC) où I est le milieu de [AB].
Pour la tracer avec une équerre, faire glisser le côté [IP] de
cette équerre jusqu'à ce que la perpendiculaire (IQ) passe par C.
6.3. Règle non graduée et équerre
Configuration du triangle équilatéral
À utiliser lorsque le segment [AB] est sur un bord de la feuille,
lorsqu'on ne sait pas placer un deuxième point de la médiatrice.
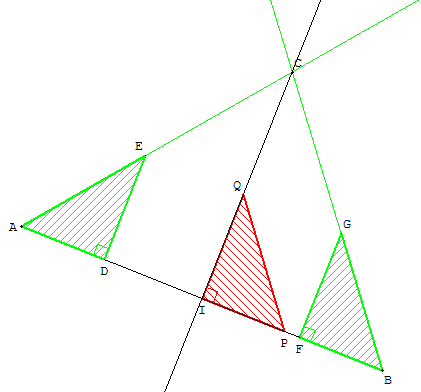
Configuration du triangle isocèle
Placer un des sommets de l'équerre en A, le petit côté [AD] de
l'équerre le long du segment [AB] et tracer la droite (AE) le long de l'hypoténuse.
Retourner l'équerre et tracer la droite (BG) en plaçant ce même sommet en B.
Les droites (AE) et (BG) se coupent en C.
Le triangle ABC, ayant deux angles égaux à celui de l'équerre, est isocèle.
C est un point de la médiatrice.
Tracer la médiatrice de [AB], en faisant glisser le côté [IP]
de l'équerre jusqu'à ce que la perpendiculaire (IQ) passe par C.
I est alors le milieu de [AB] et (IC) la médiatrice.
7. Une médiatrice uniquement à l'équerre
Pour construire la médiatrice de [AB], tracer un losange ACBD
de diagonale [AB]. La médiatrice est l'autre diagonale [CD]
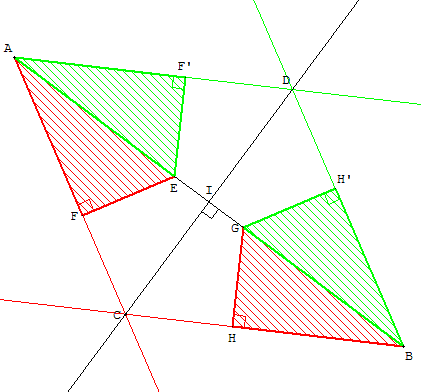
En plaçant l'hypoténuse de l'équerre le long du segment [AB]
et en posant successivement un des angles aigus en A et B,
de part et d'autre de la droite (AB), on trace un losange
ACBD de diagonale [AB].
L'autre diagonale [CD] du losange est la médiatrice cherchée.
8. Tracer un carré à la règle et l'équerre
Construction à la règle (non graduée) à partir d'un côté
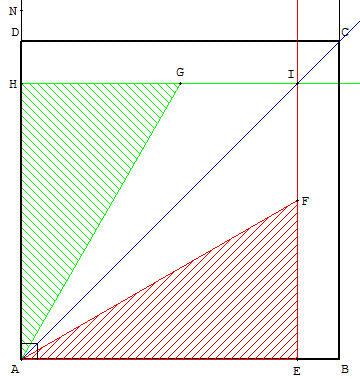
Tracer le côté [AB], puis en plaçant l'angle droit de
l'équerre en A, tracer la perpendiculaire (AN) à (AB).
Placer un des coins de l'équerre en A, un des petits
côtés [AE] sur (AB) et tracer une perpendiculaire [EF) à (AB).
Retourner l'équerre, ce même petit côté sur (AN),
tracer une deuxième perpendiculaire [HG) à (AN).
Ces deux perpendiculaires se coupent en I et font apparaître
un petit carré AEIH de diagonale [AI].
Il suffit par un agrandissement ou réduction (au lycée on parlera
d'homothétie de centre A) du carré AEIH, de trouver le carré ABCD.
Pour cela, tracer le sommet C intersection de la droite (AI),
diagonale du carré cherché, et de la perpendiculaire à (AB) en B.
La perpendiculaire à (AN) passant par C permet
de trouver le dernier sommet D du carré ABCD.
Autre tracé du carré à la règle et l'équerre
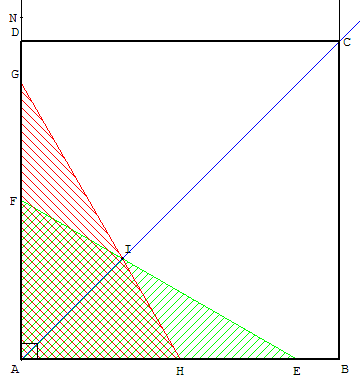
En plaçant l'angle droit d'une équerre, qui n'est pas
isocèle, en A, tracer la perpendiculaire (AN) à (AB)
et marquer l'hypoténuse [EF] sur la feuille.
Retourner l'équerre, en permutant les petits côtés,
faire un deuxième tracé de l'hypoténuse [GH].
Ces deux droites (EF) et (GH) se coupent en I et la
droite (AI) est la bissectrice de BAN. Les angles
BAI et NAI mesurent 45° et (AI) est une diagonale du carré.
Comme ci-contre, on construit le sommet C du carré,
intersection de (AI) et de la perpendiculaire à (AB)
en B, et on termine le côté [CD] du carré.
Retrouver ces constructions dans : carré avec deux sommets inaccessibles
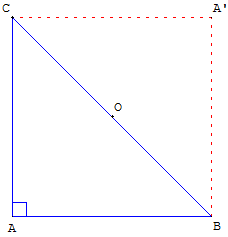
9. À la recherche du centre perdu
On ne dispose que d'une équerre et d'une règle non graduée,
retrouver le centre d'un cercle (c) ?
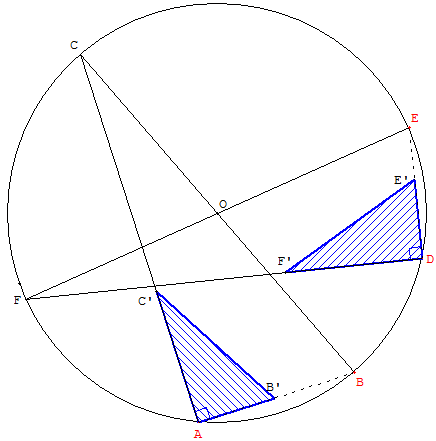
Indications
Placer deux points A et B sur le cercle et, en plaçant l'équerre
AB’C’ en A le long de (AB), tracer la perpendiculaire en A à (AB).
Cette perpendiculaire recoupe le cercle en C.
Le triangle ABC, rectangle en A, est inscrit dans un demi-cercle.
[AC] est donc un diamètre de (c).
De même construire deux autres points D et E et le triangle
rectangle DEF, inscrit dans (c).
[EF] est un deuxième diamètre.
Les deux diamètres se coupent en O, centre du cercle.
Construction avec les médiatrices de deux cordes : le cercle au collège
Construction avec la « règle à bords parallèles » : à la recherche du centre perdu
Construction du centre au « compas seul » : problème de Napoléon
Table des matières
Dans d'autres pages du site
Constructions à la règle et au compas
Collège Problèmes de construction
Tracer la perpendiculaire à une droite lorsque
le point de concours n'est pas sur la feuille.
Carré avec deux sommets inaccessibles
Construction à l'équerre du milieu d'une corde
Lieux géométriques : l'équerre contre un mur
(classes de quatrième - de seconde - épreuve pratique de terminale S)
Sur ordinateur, cette page en grand écran
Google friendly
|
|
Page no 115, réalisée le 11/12/2007 |