 Descartes et les Mathématiques
Descartes et les Mathématiques
Le cercle au collège
Dix exercices de géométrie plane sur le cercle avec la géométrie dynamique.
Sommaire
1. Définitions
– en un point du cercle
– passant par un point donné (constructions d'Euclide)
4. Une réalisation : construire un cercle tangent à trois droites
– Cercle tangent à une droite en un point de la droite,
passant par un autre point extérieur à cette droite
– Cercle tangent à deux droites sécantes, de centre donné
– Cercle tangent à deux droites, passant par un point donné
6. Tangentes communes à deux cercles
Tangente commune à deux cercles tangents
1. Définitions
Un cercle est une courbe plane constituée des points situés
à égale distance d'un point nommé centre.
La valeur de cette distance est appelée rayon.
On nomme aussi rayon un segment joignant le centre à un point du cercle.
Un diamètre est un segment d'une droite passant par le centre
et dont les extrémités sont deux points d'intersection de la
droite avec le cercle. Le diamètre est aussi la longueur de ce
segment, égale au double du rayon.
Un disque est la région du plan à l'intérieur d'un cercle.
Un arc est une partie de cercle délimitée par deux points.
Une corde est un segment joignant les extrémités d'un
arc du cercle. La corde sous-tend l'arc de cercle.
Une flèche est le segment reliant les milieux d'un arc
de cercle et de la corde qui le sous-tend.
Médiatrice d'une corde
Dans un cercle, la droite qui joint le milieu d'une corde
au centre du cercle est la médiatrice de cette corde.
Justification
Cercle de centre O.
I milieu de la corde AB.
En effet, (OI), médiane du triangle isocèle OAB,
est aussi la médiatrice de [AB].
![]() Figure interactive dans GeoGebraTube : médiatrice d'une corde
Figure interactive dans GeoGebraTube : médiatrice d'une corde
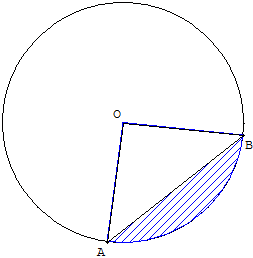
Un secteur circulaire est
une partie du disque comprise
entre deux rayons.
Un angle au centre est
l'angle formé par deux
rayons du cercle.
C'est l'angle du secteur
angulaire correspondant.
Un segment circulaire
(segment de cercle) est
la figure mixtiligne
comprise entre un arc
de cercle et la corde
qui le sous-tend
(le segment circulaire, déterminé par les points A et B,
est hachuré en bleu sur la figure ci-dessus, c'est la surface
comprise entre l'arc AB et la corde [AB]).
Un angle inscrit est un angle ayant pour sommet un point d'un
cercle, angle formé par les demi-droites joignant ce sommet
à deux autres points du cercle.
Une lunule est une portion de surface délimitée par deux
cercles non concentriques de rayons différents, formant
un croissant de lune en forme de ménisque :
convexe d'un côté et concave de l'autre.
2. Construction de cercles
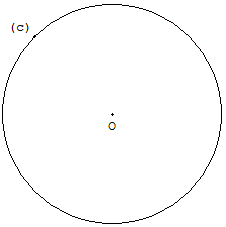
Cercle passant par un point
Deux points O et C1 du plan.
(c) est le cercle de centre O,
passant par C1.
Placer, l'étiquette (c)
sur le point C1.
Deux cercles sécants
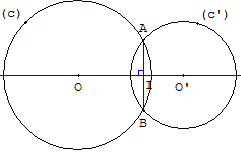
O, O’, C1, C2, sont
quatre points du plan.
Les cercles (c), de
centre O, passant
par C1,
et (c’),
de centre O,
passant par C2,
se coupent en A et B.
La ligne des centres (OO’) est la médiatrice de [AB].
Si les cercles (c) et (c’) ont pour rayons r et r’,
ils sont sécants si : |r − r’| < OO’ < r + r’
Deux cercles tangents
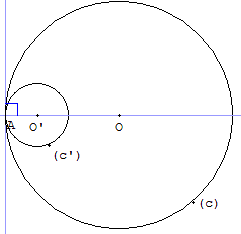
Deux points O et O’.
A est un point variable
de la droite des
centres (OO’).
Les cercles (c) et (c’)
de centres O et O’
sont tangents en A.
La perpendiculaire
en A à (OO’) est la
tangente commune
aux deux cercles.
Si les cercles (c) et (c’) ont pour rayons r et r’,
alors r + r’ = OO’ si les cercles sont tangents extérieurement,
|r − r’| = OO’ si les cercles sont tangents intérieurement.
3. Constructions géométriques de tangentes
3.a. Tangente en un point du cercle
Comment construire une tangente à un cercle
Classe de quatrième
D'un point A, situé sur un cercle de centre O, on peut mener
une tangente à ce cercle, en traçant la perpendiculaire en A au rayon [OA].
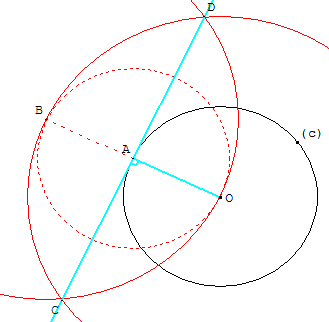
Construction à la « règle et au compas » (sans équerre).
Tracer le point B, symétrique de O par rapport à A,
puis la médiatrice de [BO].
Indications
Le point B est le deuxième point d'intersection de
la droite (OA) avec le cercle de centre A passant par O.,
passant par O, se coupent en C et D. La droite (CD),
médiatrice de [BO], est la tangente cherchée.
Construction d'un cercle de centre donné, tangent à une droite
Les cercles de centre O, passant par B, et de centre B
Étant donné une droite (d) et un point O à l'extérieur de cette
droite, tracer le point H projection orthogonale de O sur (d).
Le cercle de centre O, passant par H, est tangent à la droite (d).
3.b. Tangentes à un cercle passant par un point donné
Classe de 3e
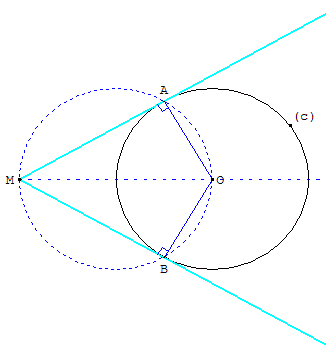
D'un point M extérieur à un cercle,
on peut mener deux tangentes à ce cercle ;
si A et B sont les points de contact avec le cercle,
les rayons [OA] et [OB] sont perpendiculaires aux tangentes
et on a MA = MB : le point M est équidistant de A et B.
Égalité des tangentes :
D'un point M, extérieur au cercle, on peut mene
deux segments tangents de même longueur.
La droite (MO) est un axe de symétrie de la figure,
c'est la bissectrice de l'angle AMB et la médiatrice de [AB].
Le quadrilatère MAOB est un cerf-volant (géométrie)
ayant deux angles droits.
C'est un carré si (OA) et (OB) sont perpendiculaires.
Euclide, livre I, proposition 17
Étant donné un cercle (c) de centre O et un point M à l'extérieur
du cercle, les points de contact A et B des tangentes issues de M
sont les points d'intersection du cercle (c) et du cercle de diamètre [MO].
Une réciproque : construction d'un cercle
de centre O tangent à une droite (MA)
Soit (c’) un cercle de diamètre [MO], A un point de ce cercle
(OA < MA) et (c) le cercle de centre O, passant par A.
La droite (MA) est tangente au cercle (c), en A.
Propriété :
Deux autres cercles tangents à ces droites
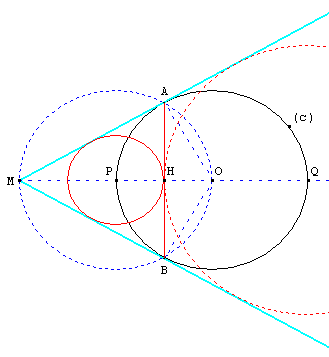
Soit P et Q les points d'intersection du cercle (c) et
de la droite (OM) et H le milieu de la corde [AB].
Les cercles de centre P et Q passant par H
sont tangents aux droites (OA) et (OB).
Le cercle de centre P est inscrit dans le triangle isocèle
MAB, le cercle de centre Q est exinscrit dans ce triangle.
3.c. Autre construction de la tangente en un point du cercle
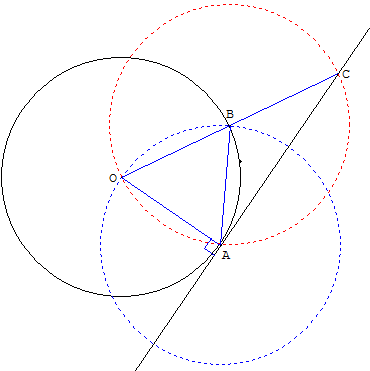
Principe : à partir du rayon [OA], tracer le triangle équilatéral
OAB, puis le triangle OAC, avec C symétrique de O par rapport
à B. OAC est un triangle rectangle en A. (AC) est la tangente en A.
À partir d'un point A du cercle (c) de centre O, placer, sur le
cercle (c), le point B tel que AB = OB. B est un des points
d'intersetion du cercle (c) et du cercle de centre A passant par O.
Soit C le point symétrique de O par rapport à B, deuxième point
d'intersection de la droite (OB) et du cercle de centre B passant
par O (et par A).
La droite (AC) est tangente au cercle en O.
Indications
OAB est un triangle équilatéral et OB = BC.
Le triangle OAC est inscrit dans le demi-cercle de centre B.
Il est rectangle en A. La droite (AC) perpendiculaire
en A au rayon [OA] est tangente au cercle.
Étude du triangle rectangle OAC : voir Géométrie en quatrième
3.d. Construction d'Euclide des tangentes issues d'un point
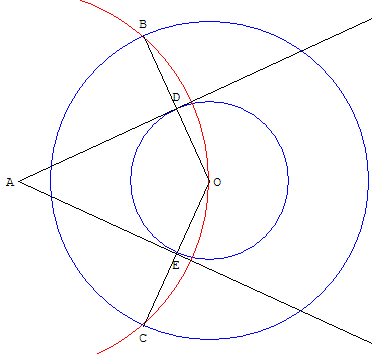
On donne un cercle (c) de centre O et de rayon r
et un point A extérieur au cercle.
Le cercle de centre O et de rayon 2r rencontre le cercle de
centre A passant par O aux points B et C.
Les segments [OB] et [OC] rencontrent le cercle (c) en D et E.
Démontrer que les droites (AD) et (AE) sont tangentes au cercle (c).
Indications
Les rayons issus de A sont de longueur égale, d'où AB = AC = AO.
Les triangles AOB et AOC sont isocèles.
OD = OE = r et OB = OC = 2r.
D et E sont les milieux de [OB] et [OC].
Les droites (AD) et (AE), médianes issues de A des triangles
isocèles AOB et AOC, sont les médiatrices de [OB] et [OC].
Elles sont perpendiculaires aux rayons (OD) et (OE).
Ces droites sont tangentes au cercle (c) en D et E.
4. Une réalisation :
construire un cercle tangent à trois droites
Les trois bissectrices intérieures d'un
triangle ABC sont concourantes en I.
Le point I est le centre du cercle inscrit dans le triangle ABC,
tangent aux trois côtés de ce triangle.
Programme de la classe de quatrième
Droites remarquables d'un triangle : construire les bissectrices,
les hauteurs, les médianes, les médiatrices d'un triangle ;
en connaître une définition et savoir qu'elles sont concourantes.
4.b. Construction avec la géométrie dynamique
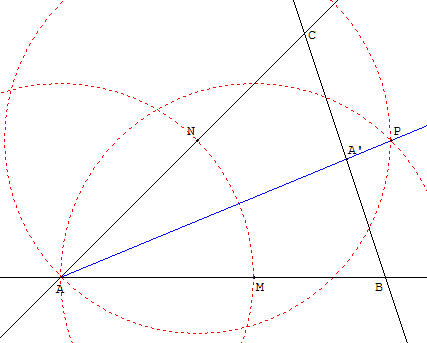
Il existe des commandes pour tracer la bissectrice d'un angle,
le cercle inscrit et le centre de ce cercle.
Il est aussi possible de réaliser la « construction
à la règle et au compas » comme suit :
Tracer la bissectrice de l'angle BAC en utilisant
la configuration du losange :
Placer un point M sur le côté (AB).
Tracer le cercle de centre A passant par M qui coupe le
deuxième côté (AC) en N.
Tracer les deux cercles de centre M et N passant par A.
Ces deux cercles se recoupent en P.
La droite (AP) est la bissectrice cherchée.
Elle coupe le côté [BC] au point A’.
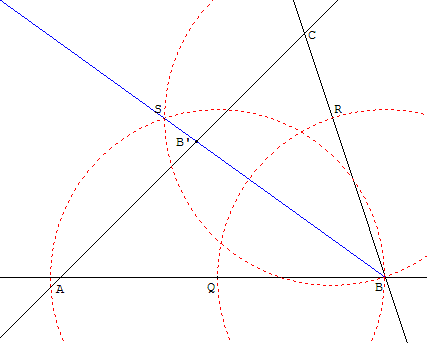
De même, tracer une deuxième bissectrice, celle de l'angle ABC.
La bissectrice (AS) coupe le côté [AC] en B’.
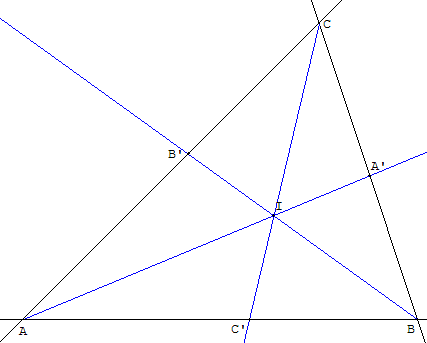
Ces deux bissectrices se coupent en I.
La droite (CI) est la troisième bissectrice.
Elle coupe [AB] en C’.
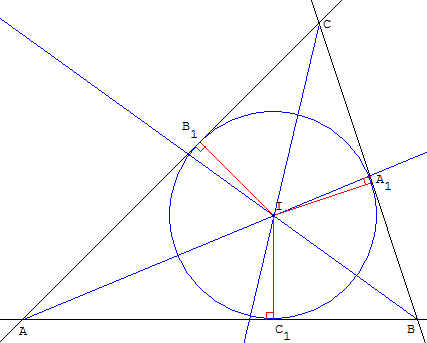
Par projection orthogonale du point I, par exemple sur le côté (AB),
on obtient un point en C1qui permet de construire le cercle inscrit.
Au lycée, on construira aussi les trois cercles exinscrits du
triangle avec les bissectrices extérieures, voir : géométrie du triangle
5. Problèmes de contact
Tracer un cercle tangent à une ou deux droites,
passant par un ou deux points.
5.1. Cercle tangent à une droite et un autre point
Cercle tangent à une droite en un point de cette droite,
passant par un autre point extérieur à la droite
Classe de quatrième
Cas particulier du problème de contact PPD :
nbsp; cercle tangent à une droite passant par deux points
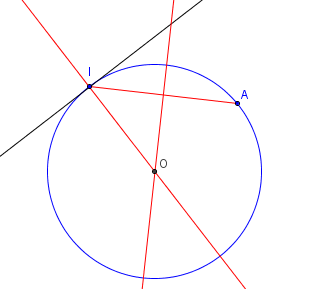
On donne une droite (d), un point I situé sur cette droite
et un point A à l'extérieur de la droite.
Tracer le cercle tangent à (d) en I, passant par A.
Indications
Tracer la droite (d’) perpendiculaire en I à (d).
Si A est sur la perpendiculaire (d’), le cercle de
diamètre [IA] est la solution.
Sinon tracer la médiatrice de [IA]. Cette médiatrice
coupe la perpendiculaire (d’) en O.
Le cercle de centre O, passant par A (et I), est l'unique solution.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
Cercle tangent à une droite et deux points
5.2. Cercle tangent à deux sécantes, de centre donné
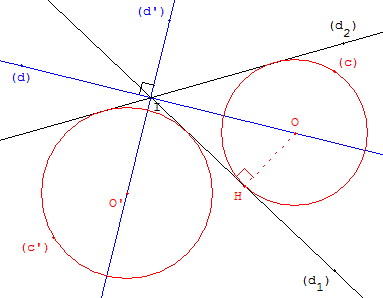
On donne deux droites (d1 ), (d2) sécantes, et un point
O de leurs bissectrices, construire un cercle tangent
à ces deux droites, centré en O.
Indications
Le centre du cercle appartient à une des bissectrices
(d) ou (d’) de l'angle des deux droites.
Le centre O étant choisi, on trouve un des points H du cercle
par projection orthogonale du centre sur une des sécantes.
5.3. Cercle tangent à deux droites, passant par un point
Tracer un cercle tangent à deux droites
Construction classique à la règle et au compas utilisant une
configuration faisant intervenir, de façon implicite, l'homothétie.
Pour le lycée, on trouve une autre construction de ce problème
de contact PDD : cercle passant par un point tangent à deux droites
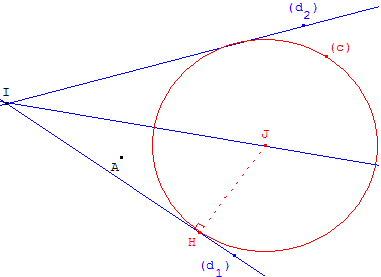
On donne deux droites (d1 ), (d2 ) sécantes et un point A
n'appartenant pas à ces droites.
Existe-t-il un cercle (c) passant par A tangent à ces deux droites ?
Combien y a-t-il de solutions à ce problème ?
Analyse
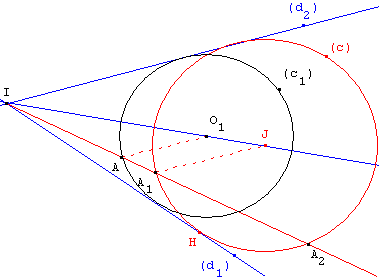
Placer un point J sur la bissectrice de (d1, d2), située dans le
même secteur angulaire que A, et tracer le cercle (c), passant
par H projection orthogonale de J sur la droite (d1).
Ce cercle est tangent aux deux droites.
Il suffit de déplacer le point J pour trouver deux solutions.
Construction
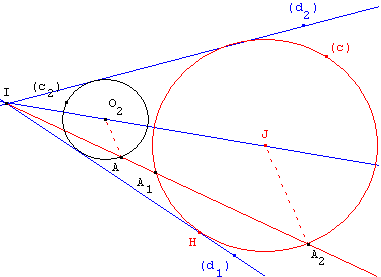
Étant donné un cercle (c), la droite (IA) rencontre (c) en deux points A1 et A2.
La droite parallèle à (A1J), passant par A, rencontre (IJ) en O1.
Le cercle (c1), de centre O1 passant par A, est tangent à (d1) et (d2).
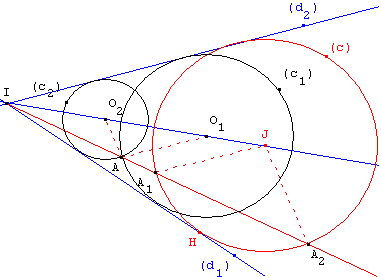
De même, la droite parallèle à (A2J), passant par A,
rencontre (IJ) en O2.
Le cercle (c2), de centre O2 passant par A, est la deuxième
solution du problème.
6. Tangentes à deux cercles
6.1. Tangentes communes à deux cercles
6.1.a. Cercles d'un même côté des tangentes
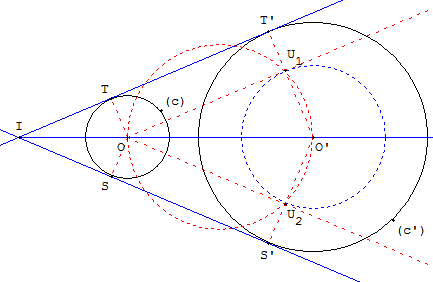
Soit (c) et (c’) sont deux cercles de centres O
et O’ et de rayons r et r’ tel que r < r’,
le petit cercle (c) n'est pas à l'intérieur de (c’) :
r + OO’ > r’.
Le cercle de centre O’ et de rayon la différence r’ − r
et le cercle de diamètre [OO’] se coupent en U1 et U2.
Les perpendiculaires, issue de O et O’ à la tangente auxiliaire
(OU1) permet de déterminer les points de contact T et T’.
La droite (TT’) est une tangente commune.
De même (OU2) permet de déterminer la tangente (SS’).
6.1.b. Tangentes entre deux cercles
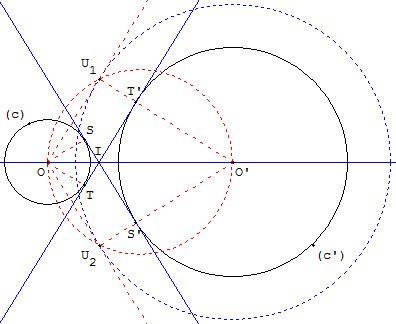
Cercles, non sécants, de part et d'autre des tangentes
Le cercle de centre O’ et de rayon la somme r’ + r et
le cercle de diamètre [OO’] se coupent en U1 et U2.
On détermine ainsi les tangentes auxiliaires (OU1) et (OU2)
qui permettent de tracer les tangentes communes (TT’) et (SS’).
Voir aussi : construction des tangentes par homothéties
Adaptation au collège de cette construction par homothéties
6.2. Tangente commune à deux cercles tangents
6.2.a. Triangle rectangle
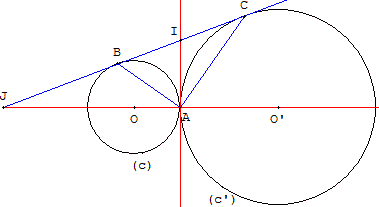
Deux cercles sont tangents extérieurement en A.
Une tangente commune à ces deux cercles touche
le premier cercle en B et le deuxième en C.
Calculer l'angle BÂC.
Solution
La tangente en A aux deux cercles coupe (BC) en I.
Les deux tangentes à (c) issues de I sont de même longueur : IB = IA.
De même, pour les tangentes au cercle (c’), on a IA = IC.
Le point A est sur le demi-cercle de diamètre [BC].
Le triangle BAC est rectangle et l'angle BÂC est droit.
6.2.b. Cercle de diamètre [OO’]
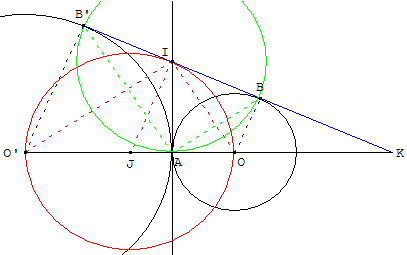
Deux cercles (c) et(c’) de centres O et O’ sont tangents
extérieurement en A. Les deux cercles sont d'un même
côté d'une tangente commune, tangente en B
au cercle (c) et en B’ au cercle(c’).
Le milieu I de [BB’] est sur la tangente en A,
commune aux deux cercles. BAB’ est un triangle rectangle
en A et le cercle de diamètre [BB’] est tangent en A à la
droite des centres (OO’).
Construction
Soit J le milieu de [OO’] et I un point d'intersection du cercle
de diamètre [OO’] et de la perpendiculaire en A à la ligne des
centres (OO’). La tangente en I à ce cercle, perpendiculaire
à (IJ) est la droite (BB’) cherchée.
6.2.c. Chercher un rectangle
Chercher un rectangle : L@ feuille à problèmes
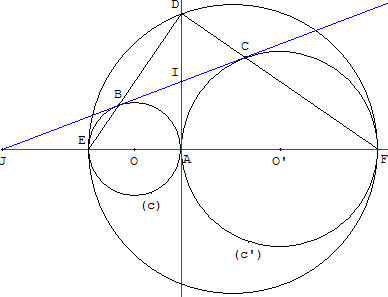
Deux cercles (c) et (c’) sont tangents en A. (c) recoupe
la ligne des centres (OO’) en E et (c’) en F.
La perpendiculaire à (OO’) passant par A coupe en D
le cercle de diamètre [EF].
Le cercle (c) coupe [ED] en B et le cercle (c’) coupe [DF] en C.
Prouver que la droite (BC) est tangente aux cercles (c) et (c’).
Preuve
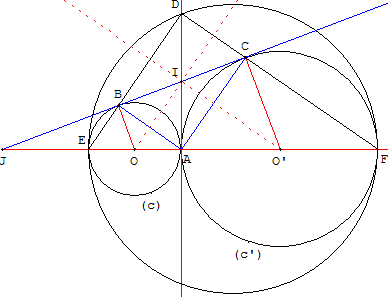
L'angle EDF, inscrit dans le demi-cercle de diamètre [EF],
est droit, de même pour EBA inscrit dans le demi-cercle
de diamètre [EA] et ACF inscrit dans le demi-cercle de diamètre [AF].
Le quadrilatère ACDB, ayant trois angles droits, est un rectangle.
Les diagonales de longueurs égales se coupent en leur milieu I et IA = IB = IC.
On a aussi OA = OB, rayon du cercle (c), donc (OI) est la médiatrice de [AB].
OAIB est un cerf-volant (géométrie) d'axe de symétrie (OI).
L'angle OBI, symétrique de OAI, est droit.
La droite (BC) est perpendiculaire au rayon [OB], elle est tangente au cercle (c).
On montre de même que O’AIC est un cerf-volant d'axe de symétrie (O’I).
La droite (BC) est perpendiculaire au rayon [O’C],
elle est tangente au cercle (c’).
7. Cercle et carré
7.a. Un carré
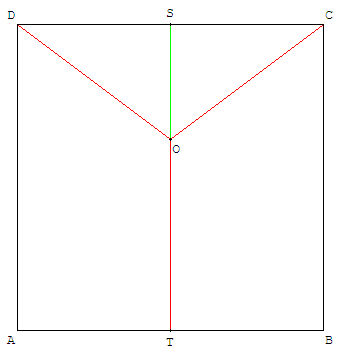
ABCD est un carré.
À l'intérieur, un point O est situé à égale distance des
sommets C et D et du milieu T de [AB].
Si OC = OD = OT = 10, montrer que le côté du carré est 16.
Indication
Étudier le triangle rectangle ayant pour hypoténuse [OA], et
comme côté la moitié de celui du carré, avec le milieu S de [CD].
Avec r = OA et x est le côté du carré, le théorème de Pythagore
dans ce triangle rectangle OSC permet d'écrire :
r2 = (x/2)2 + (x - r)2.
Équation qui a pour solution strictement positive x = 8/5 r.
Au collège on simplifie le calcul en prenant 10 pour le paramètre r
et on trouve x = 16.
7.b. Un cercle autour d'un carré
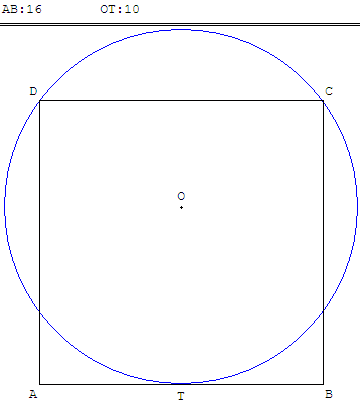
ABCD est un carré de côté 16.
Un cercle est tangent au milieu d'un des côtés du carré
et contient les deux sommets du carré.
Le cercle a pour rayon 10.
San Gaku :
Cercles tangents, tangents aux côtés d'un triangle
Trois cercles dans un cercle : théorème de Descartes
7.c. Un Sangaku simple
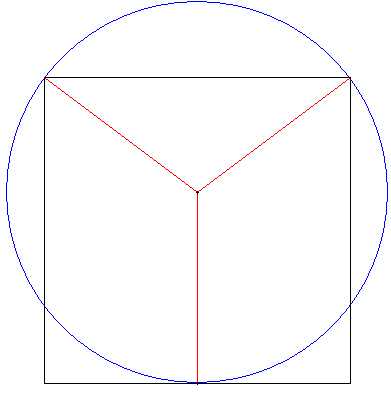
7.d. Quatre cercles autour d'un carré
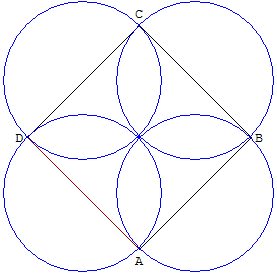
Reproduire cet autre San Gaku.
8. Triangle isocèle
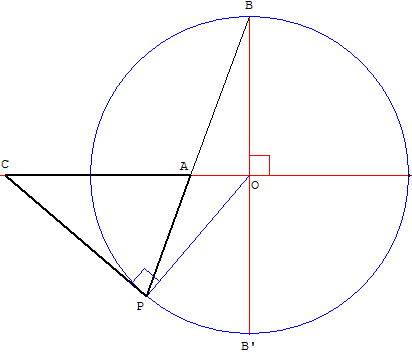
A étant un point quelconque du diamètre d'un cercle (c),
B l'extrémité d'un rayon perpendiculaire à ce diamètre,
on mène une droite (BA) qui coupe le cercle en P,
puis la tangente au point P qui coupe en C le diamètre prolongé.
Démontrer que CA = CP.
Indications
Le triangle OBP est isocèle donc OBP = OPB = α.
L'angle OPC est droit donc APC = 90° − OBP = 90° − α.
Dans le triangle rectangle OAB,
OAB = 90° − α comme complément de OBP.
Comme angles opposés par le sommet on a CAP = OAB = 90° − α.
Les angles APC et CAP étant égaux à 90° − α,
le triangle CAP est isocèle et CA = CP.
9. Projection de deux points d'un cercle
Affaire de symétrie : L@ feuille à problèmes
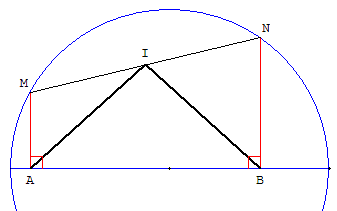
M et N sont deux points quelconques d'un cercle,
A et B leurs projections orthogonales sur
un diamètre du cercle, I le milieu de [MN].
Prouver que le triangle ABI est isocèle.
Indication
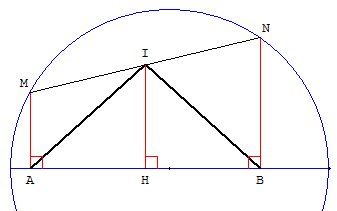
Soit H la projection orthogonale de I sur le diamètre.
Comme I est le milieu de [MN], H est le milieu de
[AB], (HI) est la médiatrice de [AB] et ABI est isocèle.
10. Retrouver le centre
10.1. Construction de deux médiatrices
Dessiner avec la géométrie dynamique
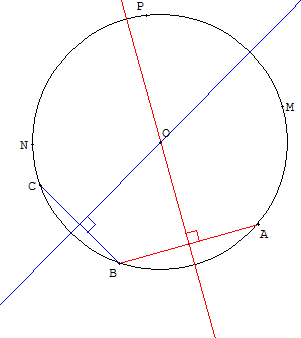
Étant donné un cercle (par exemple,
le cercle circonscrit au triangle MNP),
trouver le centre de ce cercle.
Trouver le centre avec GeoGebra
L'instruction « milieu ou centre » permet de
trouver directement le centre d'un cercle.
Dessiner les deux médiatrices
Placer trois points distincts A, B et C sur le cercle,
tracer les médiatrices des cordes [AB] et [BC].
Le point O, intersection de ces deux médiatrices,
est le centre du cercle.
![]() Figure interactive dans GeoGebraTube : centre d'un cercle
Figure interactive dans GeoGebraTube : centre d'un cercle
10.2. Dessiner les médiatrices
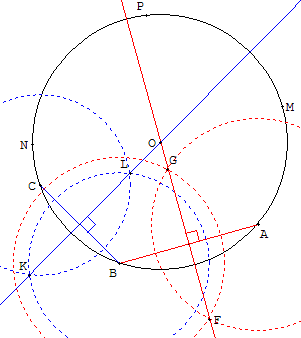
Construction à la « règle et au compas » des médiatrices
Pour la construction de la médiatrice de [AB],
tracer deux cercles de même rayon,
suffisamment grand, de centres A et B.
Ces deux cercles se coupent en F et G.
La droite (FG) est la médiatrice de [AB].
De même, pour la médiatrice de [BC],
tracer deux cercles de même rayon de centres B et C.
Ces deux derniers cercles se coupent en K et L.
La droite (KL) est la médiatrice de [BC].
Le point d'intersection O de ces deux droites
(FG) et (KL) est le centre du cercle.
Voir aussi : « règle à bords parallèles »
- À la recherche du centre perdu d'un cercle
Construction du centre au « compas seul » : problème de Napoléon
Table des matières
Dans d'autres pages du site
Tangentes communes à deux cercles
Cercle passant par trois points
Sur ordinateur, cette page pour grand écran
![]() Mobile friendly
Mobile friendly
|
|
Page no 73, |