 Descartes et les Mathématiques
Descartes et les Mathématiques
Volume d'un tronc de cylindre couché
Un cylindre couché est partiellement rempli de liquide. Quel est le volume contenu dans la cuve en fonction du niveau ?
Sommaire
1. Volume du tronc de cylindre couché
2. Calculs théoriques du volume du cylindre couché
4. Volume du cylindre couché avec un tableur
5. Volume partiel du cylindre posé horizontalement
6. Technique GéoPlan : arc de cercle - segment circulaire
1. Volume du tronc de cylindre
Problème sur la hauteur de mazout dans une cuve
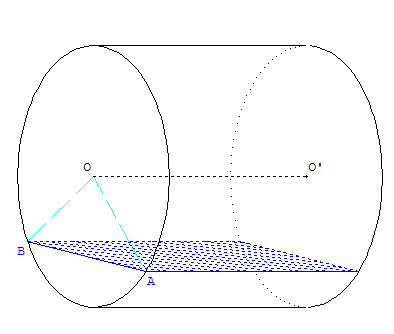
Un cylindre, de hauteur L, a pour base B un cercle de rayon R.
Son volume base × hauteur est V = B × L = π R2 × L.
La figure ci-contre représente une cuve horizontale de hauteur H = 2R et de longueur L.
Cette cuve est remplie de liquide jusqu'au niveau AB.
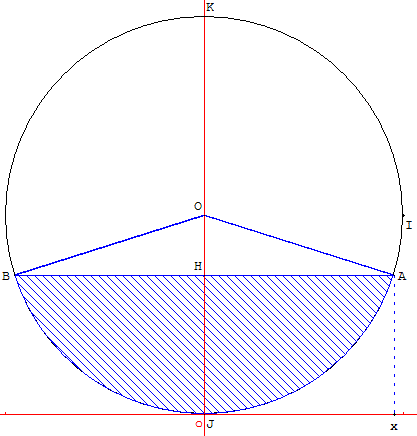
La cuve contient alors un volume b × L de liquide où b représente l'aire du segment circulaire (ou lunule) : surface hachurée comprise entre l'arc de cercle AB et la corde [AB] qui le sous-tend (figure à droite ci-dessous).
L'aire b est égale à l'aire du secteur circulaire compris entre les demi-droites [OA), [OB) et l'arc AB à laquelle selon les cas, on ajoute ou on retranche l'aire du triangle OAB.
![]() Télécharger la figure GéoSpace cuve_cyl.g3w
Télécharger la figure GéoSpace cuve_cyl.g3w
2. Calcul du volume d'un cylindre couché
Comment calculer de volume dans un réservoir horizontal ?
Où l'on trouve quatre formules avec Arc sin, Arc cos ou Arc tan :
a. V = vR2× L = (![]() ) R2× L,
) R2× L,
b. V = [2 R2 Arc tan![]() –
– ![]() (R – h)
(R – h) ![]() ] × L,
] × L,
c. V = ![]() × π R2 × L avec a = 1 –
× π R2 × L avec a = 1 – ![]() ,
,
d. V = [R2 Arc cos(1 – ![]() ) – (R – h)
) – (R – h) ![]() ] × L.
] × L.
2.a. Dans un repère d'unité égale au rayon OI, on calcule
le rapport v = ![]() tel que b = vR2 donnant un volume de liquide égal à vR2× L.
tel que b = vR2 donnant un volume de liquide égal à vR2× L.
Soit α l'angle AÔH en radians (AÔB =2α).
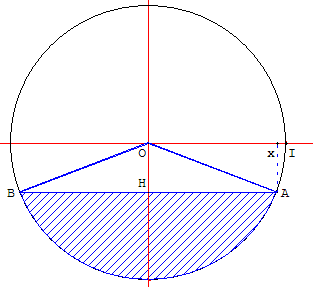
En choisissant l'unité égale à OI, on a x = HA = sin α et h = – cos α (dans ce paragraphe h varie de –1 à 1. Si H est au-dessous de O comme dans la figure ci-dessus, h est négatif).
h = – cos α donc α = Arc cos(– h), mais on préfère avec le sinus du complémentaire écrire :
h = − cos α = − sin(![]() – α) = sin(α –
– α) = sin(α – ![]() ) et donc α =
) et donc α = ![]() + Arc sin h (en radians).
+ Arc sin h (en radians).
Les coordonnées du point A(x, h) vérifient x2 + h2 = 1, donc x = ![]() .
.
L'aire du secteur circulaire est α et le triangle OAB a pour aire ![]() OH×AB (unité d'aire : le carré de côté OI).
OH×AB (unité d'aire : le carré de côté OI).
L'aire du segment circulaire hachuré est :
v = α ± ![]() OH×AB = α + h × x =
OH×AB = α + h × x = ![]() =
= ![]() .
.
En revenant aux unités d'origine on a : b = vR2 = (![]() ) R2
) R2
et un volume de liquide égal à V = vR2× L = (![]() ) R2× L
) R2× L
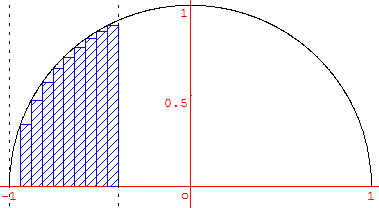
En terminale S l'aire se calcule par l'intégrale 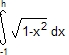 : l'intégrale de –1 à h de la fonction
: l'intégrale de –1 à h de la fonction ![]() représente l'aire comprise entre la courbe, l'axe (Ox) et les deux droites verticales d'équation x = −1 et x = h.
représente l'aire comprise entre la courbe, l'axe (Ox) et les deux droites verticales d'équation x = −1 et x = h.
Un calcul approché de cette aire par la méthode des rectangles est représenté par la figure ci-contre.
L'intégration, par parties, de v = 2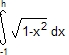 permet de retrouver exactement
permet de retrouver exactement
v = ![]() .
.
![]() Télécharger les figures GéoPlan cyl_cer1.g2w, integrale_un_moins_x2.g2w
Télécharger les figures GéoPlan cyl_cer1.g2w, integrale_un_moins_x2.g2w
2.b. Autre calcul de volume d'un cylindre couché
Trouver le volume d'une partie de cylindre, avec une intégrale
Par Michel Tornier, Commandant MONTE D'ORO
Le cercle de centre O et de rayon R a pour équation de cercle
x2 + y2 = R2.
Par un changement d'origine J(– R, 0) l'équation du cercle devient
x2 + y2 = 2Rx.
L'équation du quart d'arc de cercle positif JI dans le repère (J, x, O) est alors y = ![]() .
.
L'aire du segment circulaire hachuré est pour une sonde verticale H est alors le double l'intégrale de 0 à h de 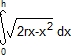 .
.
Une intégration par partie permet de trouver :
B = 2 R2 Arc tan![]() –
– ![]() (R – h)
(R – h) ![]()
2.c. Le calcul de la primitive de ![]() se fait aussi avec un changement de variable en posant sin u = 1 –
se fait aussi avec un changement de variable en posant sin u = 1 – ![]() .
.
On trouve alors le pourcentage du volume avec la formule :
![]() où a = 1 –
où a = 1 –![]() est le cosinus de α.
est le cosinus de α.
2.d. Calcul du volume du cylindre sans intégrale
L'aire b du segment circulaire est égale à l'aire du secteur circulaire compris entre les demi-droites [OA), [OB) et l'arc AB à laquelle selon les cas, on ajoute ou on retranche l'aire du triangle OAB.
En fait, on calcule la moitié de b en cherchant l'aire hachurée en bleu du triangle curviligne HAJ égale à l'aire du secteur circulaire compris entre les demi-droites [OA), [OJ) plus ou moins l'aire du triangle OHA.
Soit α l'angle AOJ en radians. Le secteur angulaire a pour aire ![]() R2α.
R2α.
Mais comme cos α = ![]() =
= ![]() = 1 –
= 1 – ![]() , on a α = Arc cos (1 –
, on a α = Arc cos (1 – ![]() ).
).
AH est la hauteur du triangle rectangle AJK, donc AH2 = HJ × HK = h(2R – h) donc AH = ![]() .
.
Le triangle OHA a pour aire ![]() OH × AH =
OH × AH = ![]() |R – h|
|R – h| ![]() .
.
L'aire b = R2 Arc cos(1 –![]() ) – (R – h)
) – (R – h) ![]() ; l'aire du triangle se retranche ou s'ajoute selon le signe de (R – h).
; l'aire du triangle se retranche ou s'ajoute selon le signe de (R – h).
Le volume s'obtient en multipliant par L.
3. Hauteur de jauge
Cylindre horizontal : volume par rapport à la hauteur
Problème sur la hauteur d'e liquiude dans un cylindre horizontal
Visualisation du volume d'un cylindre couché
Formule du volume d'un cylindre couché
Soit une cuve de hauteur JK = 2R.
Dans le paragraphe 2, les calculs théoriques ont été faits avec un paramètre h variant de –1 à 1.
Dans la suite de cette page, les calculs pratiques se font avec un nouveau paramètre
h = ![]() =
= ![]() .
.
h est positif, variant de 0 à 2, et est égal à la hauteur du liquide divisé par le rayon de la cuve.
On calcule alors v = 2 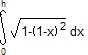 =
= ![]() .
.
![]() Télécharger la figure GéoPlan cyl_cer2.g2w
Télécharger la figure GéoPlan cyl_cer2.g2w
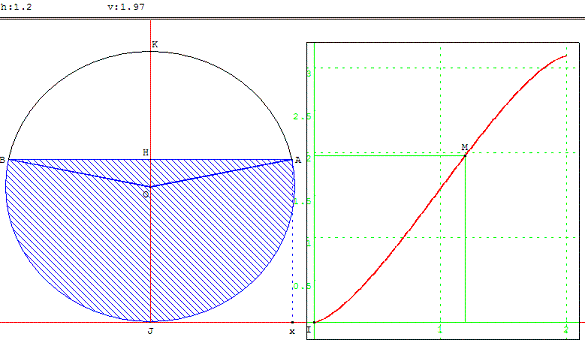
Le multiplicateur v, variant de 0 à π, est donné par la fonction dont le graphe est représenté ci-dessus avec GéoPlan et ci-dessous avec le logiciel Derive :
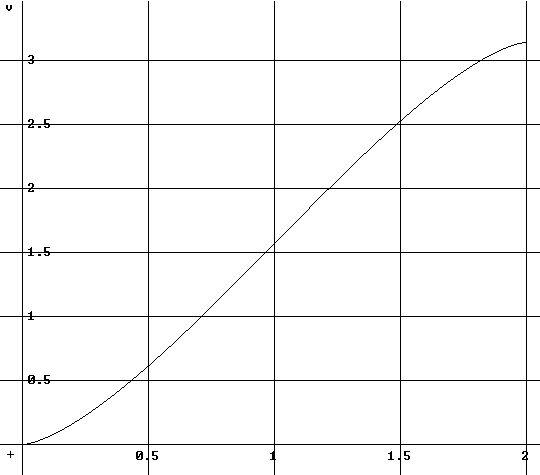
Pour ne pas trop compliquer les calculs, le paramètre h de ce paragraphe a été choisi variant entre 0 et 2. Dans la pratique, les jauges étant souvent étalonnées de 0 à 1, on divise par 2 et on calcule sur des fractions de la hauteur de la cuve en utilisant ![]() qui varie de 0 à 1.
qui varie de 0 à 1.
Pour une hauteur H de la jauge, on a h = ![]() . Cela représente une fraction
. Cela représente une fraction ![]() de la hauteur de la cuve,
de la hauteur de la cuve,
le volume de liquide est alors V = v R2 × L conformément au tableau suivant :
h/2 |
v |
h/2 |
v |
| 0,05 | 0,05872590703 | 0,55 | 1,770462497 |
| 0,1 | 0,1635011092 | 0,6 | 1,968113433 |
| 0,15 | 0,2954988410 | 0,65 | 2,161670748 |
| 0,2 | 0,4472952192 | 0,7 | 2,348919236 |
| 0,25 | 0,6141848510 | 0,75 | 2,527407813 |
| 0,3 | 0,7926734274 | 0,8 | 2,694297445 |
| 0,35 | 0,9799219153 | 0,85 | 2.846093824 |
| 0,4 | 1,173479230 | 0,9 | 2.978091557 |
| 0,45 | 1,371130166 | 0,95 | 3,082866760 |
| 0,5 | 1,570796331 | 1 | 3,141592687 |
4. Volume d'un cylindre couché avec un tableur
Bonjour
c'est avec plaisir que je suis tombé sur votre page, car elle correspond à mon problème : déterminer le volume d'engrais liquide (je suis agriculteur) qui reste dans ma cuve. Le pb est que je ne suis pas très calé en math. Quelle est la formule la plus simple à appliquer ?
Par exemple, si ma cuve couchée fait 5 mètres de diamètre et 22 mètres de long. Je mesure 1,75 mètre dans ma cuve, quel est le volume restant dans la cuve
L'objectif étant de créer une jauge.
Merci de votre aide
Laurent.
Solution : volume d'une portion de cylindre
Les données du problème sont L = 22 et 2R = 5, d'où R = 2,5.
Dans le tableau suivant, on lit que 1,75 m de hauteur de la jauge correspond à un volume de 135 m3.
En effet, on a calculé R2 × L = 137,5 et, en multipliant par π, le volume de la cuve est V = π R2 × L = 432 m3.
Pour une hauteur H = 1,75 alors 1,75/5 = 0,35 = ![]() . h = 0,7 et,
. h = 0,7 et,
en multipliant par v = 0,979,
on trouve le volume restant égal à 0,979 × 137,5 = 135 m3.
h/2 |
H |
v |
V |
h/2 |
H |
v |
V |
| 0,05 | 0,25 | 0,058 |
8 |
0,55 | 2,75 | 1,770 | 243 |
| 0,1 | 0,5 | 0,163 |
22 |
0,6 | 3 | 1,968 | 271 |
| 0,15 | 0,75 | 0,295 |
41 |
0,65 | 3,25 | 2,161 | 297 |
| 0,2 | 1 | 0,447 |
62 |
0,7 | 3,5 | 2,348 | 323 |
| 0,25 | 1,25 | 0,614 |
84 |
0,75 | 3,75 | 2,527 | 348 |
| 0,3 | 1,5 | 0,792 |
109 |
0,8 | 4 | 2,694 | 370 |
| 0,35 | 1,75 | 0,979 |
135 |
0,85 | 4,25 | 2.846 | 391 |
| 0,4 | 2 | 1,173 |
161 |
0,9 | 4,5 | 2.978 | 409 |
| 0,45 | 2,25 | 1,371 |
189 |
0,95 | 4,75 | 3,082 | 424 |
| 0,5 | 2,5 | 1,570 |
216 |
1 | 5 | 3,141 | 432 |
Cas particulier
Pour un cas particulier il suffit avec un tableur de recopier le tableau ci-dessous en complétant la deuxième colonne en multipliant par la hauteur de la cuve avec la formule :
= C(–1)L * 5 (multiplier la cellule de gauche par la hauteur 5 de la cuve et recopier la formule 20 fois vers le bas)
ou avec une référence absolue :
= A2 * 5
Calculer W = R2 × L (dans l'exemple précédent, on trouve 137,5). Compléter la quatrième colonne en multipliant ce résultat par le coefficient v avec la formule :
= C(–1)L * 137,5 (multiplier la cellule v = 0,058 par R2 × L soit 137,5 et recopier la formule 19 fois vers le bas)
ou
= C2 * 137,5
A |
B |
C |
D |
|
1 |
h/2 |
H |
v |
V |
2 |
0,05 |
0,058 |
||
3 |
0,1 |
0,163 |
||
4 |
0,15 |
0,295 |
||
5 |
0,2 |
0,447 |
||
6 |
0,25 |
0,614 |
||
7 |
0,3 |
0,792 |
||
8 |
0,35 |
0,979 |
||
9 |
0,4 |
1,173 |
||
10 |
0,45 |
1,371 |
||
11 |
0,5 |
1,570 |
||
12 |
0,55 |
1,770 |
||
13 |
0,6 |
1,968 |
||
14 |
0,65 |
2,161 |
||
15 |
0,7 |
2,348 |
||
16 |
0,75 |
2,527 |
||
17 |
0,8 |
2,694 |
||
18 |
0,85 |
2.846 |
||
19 |
0,9 |
2.978 |
||
20 |
0,95 |
3,082 |
||
21 |
1 |
3,141 |
La première colonne A du tableur ci-dessus contient ![]() de 0,05 à 1, avec 21 graduations pour la jauge ce qui est souvent suffisant.
de 0,05 à 1, avec 21 graduations pour la jauge ce qui est souvent suffisant.
Dans la colonne B, on calcule H = h/2 * D avec les formules = C(–1)L * D ou = A2 * L à recopier vers le bas.
Dans la colonne C, on trouve le calcul du multiplicateur v avec la formule ![]() .
.
Les habitués de tableur utiliseront la formule :
= ASIN(2*C(–2)L – 1) + PI()/2 + (2*C(–2)L – 1) * SQRT(2*C(–2)L *(2 –C(–2)L)) avec des adresses de cellule relatives.
Avec des adresses absolues nous obtenons dans la cellule C2 la formule :
= ASIN(2*A2 – 1) + PI()/2 + (2*A2 – 1) * RACINE(2*A2 *(2 – 2*A2))
Dans la colonne D, on calcule V= v * R2 × L = v * W avec les formules
= C(–1)L * W ou = C2 * W à recopier vers le bas.
Dans les tableaux, à télécharger ci-dessous, modifier cellule F2 la valeur de L et cellule F3 la valeur de D.
![]() Télécharger le tableau OpenOffice volume_cylindre.ods
Télécharger le tableau OpenOffice volume_cylindre.ods
Télécharger le tableau Excel volume_cylindre.xls
5. Volume partiel d'un cylindre posé horizontalement
Bonjour
tout d'abord merci pour la qualité de votre site.
Mais malheureusement étant nul en math je n'ai pas réussi à calculer la formule dont j'ai besoin.
Vous serait-il possible de m'aider sachant que :
j'ai une cuve à fioul avec un fond de cuve.
elle a une contenance de 3000 litres
un diamètre de 120 cm
une longueur de 230 cm
J'ai un niveau de fioul au fond de 30 cm et j'aimerai savoir ce que cela peut représenter en quantité.
Merci pour votre aide.
Solution : tableau des valeurs du volume en fonction de la hauteur de la jauge
Multiplier les cellules de gauche par la hauteur 1,2.
Calculer R2 × L (on trouve 0,828). Compléter la quatrième colonne en multipliant le coefficient v de la troisième colonne par ce résultat 0,828.
h/2 |
H |
v |
V |
0,05 |
0,06 |
0,058 |
0,049 |
0,1 |
0,12 |
0,163 |
0,135 |
0,15 |
0,18 |
0,295 |
0,245 |
0,2 |
0,24 |
0,447 |
0,370 |
0,25 |
0,30 |
0,614 |
0,509 |
0,3 |
0,36 |
0,792 |
0,656 |
0,35 |
0,42 |
0,979 |
0,811 |
0,4 |
0,48 |
1,173 |
0,972 |
0,45 |
0,54 |
1,371 |
1,135 |
0,5 |
0,60 |
1,570 |
1,301 |
0,55 |
0,66 |
1,770 |
1,466 |
0,6 |
0,72 |
1,968 |
1,630 |
0,65 |
0,78 |
2,161 |
1,790 |
0,7 |
0,84 |
2,348 |
1,945 |
0,75 |
0,90 |
2,527 |
2,093 |
0,8 |
0,96 |
2,694 |
2,231 |
0,85 |
1,02 |
2.846 |
2,357 |
0,9 |
1,08 |
2.978 |
2,466 |
0,95 |
1,14 |
3,082 |
2,553 |
1 |
1,20 |
3,141 |
2,601 |
On peut lire sur le tableau ci-dessus qu'un fond de 30 cm correspond à un demi-mètre cube (509 litres).
Technique GéoPlan
6. Arc de cercle - segment circulaire ou segment de cercle
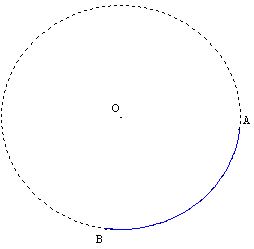
Arc de cercle : un arc est une partie de cercle délimitée par deux points.
Pour GéoPlan les arcs sont orientés et tracés dans le sens trigonométrique en partant du premier point nommé (l'origine) vers le deuxième point (l'extrémité).
Tracé d'un arc non orienté
Placer deux points A1 et B1 à la place de A et B tels que l'arc A1B1 soit direct.
Lorsque l'angle t = (![]() ,
, ![]() ) est positif, µ(t>0) = 0, les translations de vecteur nul créent deux points A1 et B1 à la place de A et B.
) est positif, µ(t>0) = 0, les translations de vecteur nul créent deux points A1 et B1 à la place de A et B.
Lorsque t est négatif, µ(t<0) = 1, les translations de vecteurs ![]() et
et ![]() placent A1 et B1 à la place de B et A.
placent A1 et B1 à la place de B et A.
Voici les instructions GéoPlan :
t mesure de l'angle de vecteurs (vec(O,A),vec(O,B)) en radian A1 image de A par la translation de vecteur µ(t<0)*vec(A,B) Objet dessinable A1, particularités: non dessiné B1 image de B par la translation de vecteur µ(t<0)*vec(B,A) Objet dessinable B1, particularités: non dessiné a arc d'origine A1 et d'extrémité B1 sur le cercle c
![]() Télécharger la figure GéoPlan arc.g2w
Télécharger la figure GéoPlan arc.g2w
Secteur circulaire : partie du disque comprise entre deux rayons.
Segment circulaire (segment de cercle) : dans un cercle, figure mixtiligne comprise entre un arc de cercle AB et la corde [AB] qui le sous-tend.
Calcul de l'aire d'un segment de cercle :
L'aire du segment circulaire AB, sur un cercle de centre O, est celle du secteur circulaire compris entre les demi-droites [OA), [OB) et l'arc AB à laquelle selon les cas, on ajoute (figure 4 ci-dessous) ou on retranche (figure 2) l'aire du triangle OAB.
Réalisation d'un segment circulaire avec GéoPlan :
a arc d'origine A et d'extrémité B sur le cercle c Objet dessinable a, particularités: bleu, hachures diagonales t mesure de l'angle de vecteurs (vec(O,A),vec(O,B)) en radian A1 image de A par la translation de vecteur vec(A,A)/µ(t>0) Objet dessinable A1, particularités: non dessiné t1 polygone OA1B Objet dessinable t1, particularités: rempli avec la couleur du fond A2 image de A par la translation de vecteur vec(A,A)/µ(t<0) Objet dessinable A2, particularités: non dessiné t2 polygone OA2B Objet dessinable t2, particularités: bleu, hachures diagonales
Lorsque l'arc est plus petit qu'une demi-circonférence, l'angle t est positif, µ(t>0) vaut 1, la translation de vecteur nul vec(A,A)/µ(t>0), créé un point A1 à la place de A et le triangle t1 = OA1B = OAB créé avec la couleur de fond efface les hachures sur OAB.
µ(t<0) vaut 0, la translation de vecteur vec(A,A)/µ(t<0) n'existe pas, pas de point A2 ni de triangle t2.
Lorsque l'arc est plus grand qu'une demi-circonférence, l'angle t est négatif, µ(t>0) vaut 0, la translation de vecteur vec(A,A)/µ(t>0) n'existe pas, pas de point A1 ni de triangle t1.
µ(t<0) vaut 1, la translation de vecteur nul vec(A,A)/µ(t<0), créé un point A2 à la place de A et le triangle t2 = OA2B = OAB complète les hachures sur OAB.
Coloriage d'un secteur circulaire
Figure 1
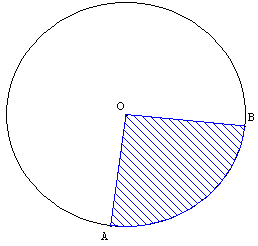
Avec GéoPlan, un motif sur arc AB d'un cercle de centre O hachure le secteur circulaire compris entre les demi-droites [OA), [OB) et l'arc avec l'instruction :
a arc d'origine A et d'extrémité B sur le cercle c Objet dessinable a,
particularités: bleu, hachures diagonales
Coloriage d'un segment circulaire
Figure 2
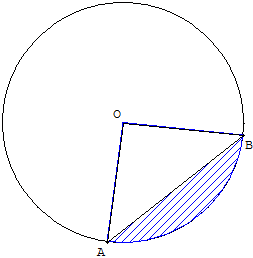
Instruction GéoPlan pour la suppression des hachures sur le triangle OAB :
t polygone OAB Objet dessinable t, particularités: rempli avec la couleur du fond
Figure 3
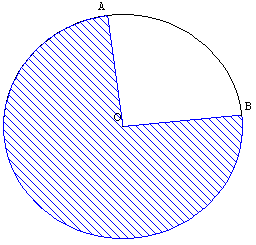
Coloriage d'un secteur circulaire d'un arc de longueur supérieure à la demi-circonférence.
Figure 4
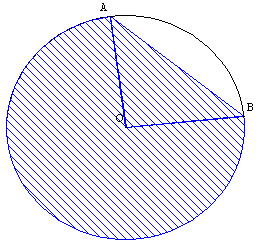
Coloriage d'un segment circulaire d'un arc de longueur supérieure à la demi-circonférence
Le triangle OAB est colorié avec le même motif que l'arc.
![]() Télécharger la figure GéoPlan seg_cir.g2w
Télécharger la figure GéoPlan seg_cir.g2w
Table des matières
Téléchargement
![]() Télécharger volume_integrale.doc : ce document au format « .doc »
Télécharger volume_integrale.doc : ce document au format « .doc »
![]() Télécharger volume_integrale.pdf : ce document au format « .pdf »
Télécharger volume_integrale.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image,
mais Google trouve une erreur de type "soft 404".
La copie ne devrait pas être référencée et
Google devrait choisir l'original au lieu du piratage !
Copyright 2005 - © Patrice Debart
Expressions clefs : volume cylindre couché,
volume partiel d'un cylindre, volume d'une cuve horizontale,
calcul volume réservoir horizontal,segment circulaire
Excel : cylindre horizontal volume par rapport hauteur
On plonge dans l'eau cylindre de bois de diamètre d.
Calculer la hauteur h de la partie immergée.
Données numériques: d = 20cm ; densité du bois 0,65
![]() Google friendly
Google friendly
|
|
Page no 86, créée le 7/10/2005 |