Descartes et les Mathématiques

Calcul d'intégrales
avec la méthode des trapèzes

Géométrie plane en terminale S :
deux exercices et le calcul approché d'intégrales avec GéoPlan.

Sommaire

1. Intégrale de f entre a et b par la méthode des rectangles

f(x) =

2. Encadrement

2.1. f(x) = x²
2.2. f(x) =

3. Méthode des trapèzes f(x) =

Intégration

1. Intégrale de f entre a et b par la méthode des rectangles

    f(x) =

Avec le menu :
créer>numérique>fonction numérique>une variable, modifier la fonction f.

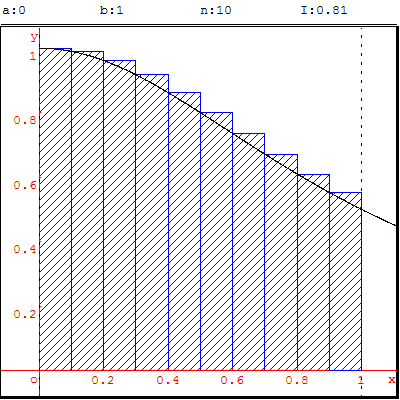
Calcul d'une valeur approchée d'intégrale

On décompose le segment [a, b] en n segment de même longueur h = (b−a)/n
et on note u₀ = a, u₁, u₂, u₃…, u_n = b, la suite des extrémités de ces intervalles.

Pour une valeur x₀ égale à un des u_i on trace
deux extrémités A(x₀, 0) et A’(x₀+h, 0) sur l'axe (Ox),
Les points M(x₀, f’(x₀)) et M’(x₀+h, f’(x₀))
permettent de tracer le rectangle AA’M’M nommé R.
Les points N(x₀, f’(x₀+h)) et N’(x₀+h, f’(x₀+h))
permettent de tracer le rectangle AA’N’N nommé R’.

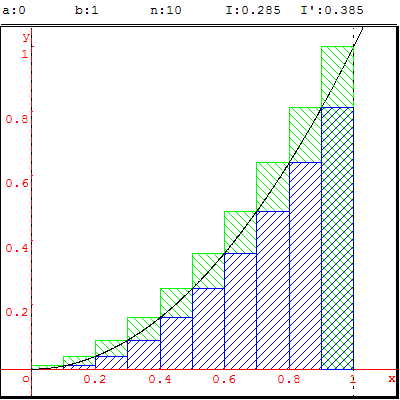
2. Encadrement

Comme en mode trace, un rectangle AA’N’N
efface le rectangle AA’M’M précédent,
il faut deux programmes distincts pour les fonctions croissantes sur [a, b]
et pour les décroissantes où les rôles de R et R’ sont échangés.

2.1. Fonction croissante : f(x) = x² sur R⁺

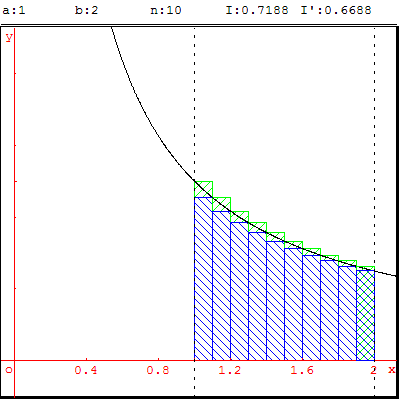
2.2. Fonction décroissante : f(x) =

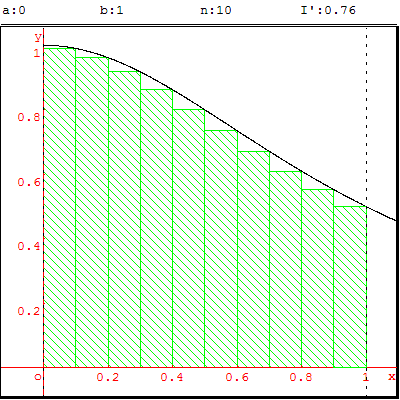
3. Méthode des trapèzes

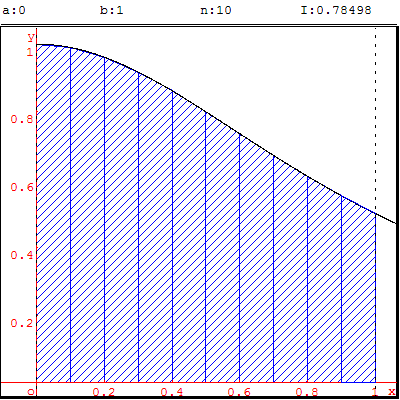
Une valeur approchée de l'intégrale se trouve en faisant
la somme des aires des trapèzes AA’M’M de sommets, pour une valeur x₀,
les points A(x₀, 0) et A’(x₀+h, 0) sur l'axe (Ox)
et les points M(x₀, f’(x₀)) et M’(x₀+h, f’(x₀+h)).

Pour la fonction f(x) = , étudiée ci-contre sur [0, 1],
on a une excellente approximation sachant que ≈ 0,7853.

Table des matières

Voir dans d'autres pages du site

Mathématiques en terminale

Tangente à une courbe

Épreuve pratique :

Famille de cercles

Recherche d'un lieu géométrique

La géométrie à l'épreuve pratique

Épreuve pratique dans l'espace 2009

Mobile friendly ; sur ordinateur : version desktop