René Descartes Descartes et les Mathématiques

Constructions élémentaires

à la « règle et au compas »

Deux constructions au collège avec la géométrie dynamique : hauteur, division d'un segment…

Constructions géométriques

1. Hauteur d'un triangle

2. Diviser un segment en parties égales

Voir aussi dans d'autres pages du site

Partage d'un segment en trois

Partages du cercle en 2, 3, 4, 6…

Partage du demi-cercle en trois, en cinq…

Médiatrice d'un segment

Losange à partir d'une diagonale

Constructions géométriques de tangentes : voir cercle au collège

Construction uniquement à la règle seule

Report d'un angle

Constructions de perpendiculaires et de parallèles :

Perpendiculaire abaissée d'un point sur une droite

Perpendiculaire élevée d'un point à une droite

Parallèle à une droite passant par un point donné

Parallèle à une droite située à une distance donnée

en : compass and straightedge constructions.
de : Konstruktion mit Zirkel und Lineal.

À l'école les constructions géométriques de figures simples à la règle, à l'équerre et au compas sont au programme du cours moyen.
Il est essentiel de montrer que le compas ne sert pas uniquement à tracer des cercles, mais aussi à reporter des longueurs égales.

1. Construction d'une hauteur d'un triangle

construction elementaire - tracer une hauteur au compas - copyright Patrice Debart 2003

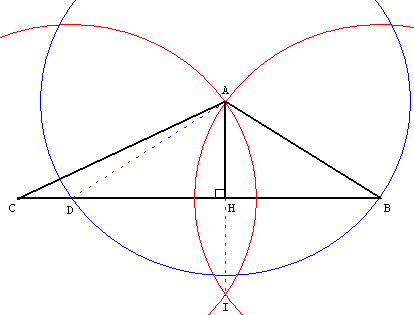
Comment tracer les hauteurs d'un triangle avec un compas

Pour tracer des droites perpendiculaires à la « règle et au compas », il faut souvent se ramener à la construction de la médiatrice d'un segment.

Pour trouver, à la « règle et au compas », la hauteur relative au côté [BC] d'un triangle ABC tel que AC > AB, construire un triangle isocèle ABD où le point D est l'intersection du cercle de centre A passant par B avec la droite (BC).

Avec les cercles de centres B et D passant par A, tracer la médiatrice (AI) de [BD]. Le point I, deuxième point d'intersection de ces deux derniers cercles, est le symétrique de A par rapport à la droite (BC).

La médiatrice (AI) coupe (CD) en H et (AH) est la hauteur cherchée.

2. Partage d'un segment en parties égales

Diviser un segment [AB] en n parties égales

Classes de quatrième et troisième

2.a. Configuration de Thalès

construction elementaire - division d'un segment en cinq - copyright Patrice Debart 2003

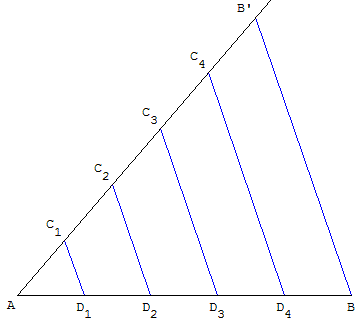
Cet exercice repose sur la propriété de Thalès, mais peut être utilisé avant de l'avoir justifiée.

Comment partager un segment en 5 parties égales

Tracer sur demi-droite issue de A, 5 segments égaux [AC₁], [C₁C₂]…, [C₄B’].

Cas général : partager un segment en n parties égales

Tracer sur demi-droite issue de A, n segments de mêm longueur [AC₁], [C₁C₂]…, [C_n-1B’].
Ce tracé se fait facilement, à la règle et au compas : placer un point C₁ à l'extérieur de (AB), et sur la demi-droite [AC₁), tracer le symétrique C₂ de A par rapport à C₁, puis le symétrique C₃ de C₁ par rapport à C₂ et ainsi de suite jusqu'à B’.

Tracer le segment [BB’] et les parallèles à (BB’),
passant par C₁, C₂…, C_n-1.

Les points D₁, D₂…, D_n-1 partagent [AB] en n parties égales.

Cas partiliers : partager un segment en 4 parties égales
Comme ci-dessus, tracer 4 segments égaux [AC₁], [C₁C₂], [C₂C₃], [C₃B’].

partage d'un segment en trois

Télécharger la figure GéoPlan diviser_segment.g2w

Méthode de la règle à bords parallèles : partage d'un segment en parties égales

3.b. Construction d'une des parallèles

construction elementaire - diviser un segment aux deux-cinquiemes - copyright Patrice Debart 2003

Pour trouver avec précision une des divisions sur le segment [AB],
par exemple ici le point D₂ aux deux cinquièmes de [AB], utiliser la construction suivante :

Placer, comme ci-contre à gauche, n points (5 points) sur [AB’].
Placer deux points M et N sur [BB’] tel que BM = MN.

Tracer le symétrique P de B par rapport à C₂, puis le milieu I de [PN].

La droite (IC₂) coupe (AB) en D₂ situé aux 2 n^ième de [AB]. (Dans la figure ci-dessus, D₂ est situé aux de [AB])