Descartes et les Mathématiques

Constructions à la règle à deux bords parallèles

Constructions uniquement avec une règle, non graduée, à deux bords parallèles.

Sommaire

1. Configuration du losange
    a. Bissectrice d'un angle
    b. Médiatrice
2. Partage d'un segment en n parties égales

3. Milieu d'un segment
    a. Construction de Hilbert
    b. Milieu d'une corde
4. À la recherche du centre perdu d'un cercle

5. Tiers d'un segment

6. Parallèle à une droite

7. Symétrique d'un point par rapport à une droite
    Perpendiculaire abaissée d'un point sur une droite
8. Triangle équilatéral dans une bande rectangulaire
    Triangle équilatéral avec la règle à bords parallèles
9. Construction du pentagone régulier

0. La règle avec deux bords parallèles

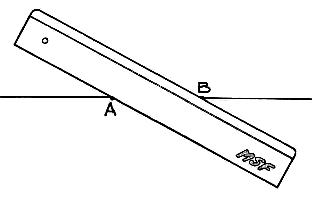
Avec seulement une règle, à bords parallèle, de largeur l, on peut :
    • tracer une droite par deux points connus ;
    • tracer une droite parallèle à une droite connue, à distance égale à largeur de la règle ;
    • tracer par deux points A et B, tels que AB > l, une droite telle que le point A est sur un des bords de la règle et B sur l'autre bord.

On a la structure affine du plan : la règle à bords parallèles seule permet toutes les constructions de points et de droites constructibles à la règle et au compas.
Dans la pratique, en raison de la complexité des constructions, c'est souvent inutilisable. Nous présentons dans cette page huit constructions relativement simples.

Constructions de la règle

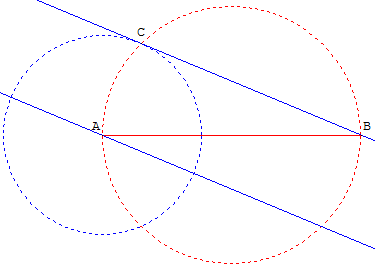
Construction de la règle passant par deux points situés sur les deux bords

Avec GéoPlan, pour placer une règle à bords parallèles entre deux points A et B (AB ≥ l), nous tracerons le cercle de diamètre [AB] puis, par exemple, le cercle de centre A et de rayon l.

Choisir le point C, un des points d'intersection de ces deux cercles. C est situé sur un des bords de la règle.

L'autre bord s'obtient en traçant la parallèle à (BC) passant par A.

Télécharger la figure GéoPlan deux-points_sur_2bords.g2w

Construction avec trois cercles

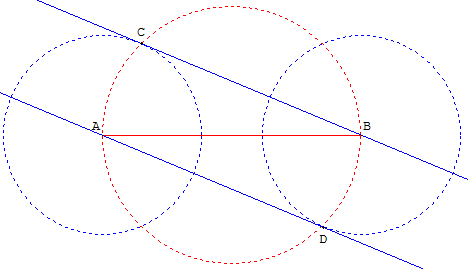
L'autre bord peut aussi s'obtenir en traçant le cercle de centre B et de rayon l, avec le point d'intersection D des cercles, et tracer le bord (AD).

Télécharger la figure GéoPlan deux-points_sur_2bords2.g2w

Remarque : il est clair que ces outils cercle ne font pas partie de la géométrie de la règle et les constructions sont à gommer.

Avec GéoPlan, nous simulerons la règle, de largeur l = 1, avec la macro « règle à bords parallèles » qui, à partir d'un des bords (d₁), tracera l'autre bord une droite (d₂) avec l'instruction :

d2 deuxième bord de la règle d1.

L'orientation induite par GéoPlan sur la droite (d₁) déterminant le côté où la règle sera tracée.

1. Configuration du losange

Construction avec une bande parallèle :
l'intersection de deux bandes parallèles de même largeur est toujours un losange.

1.a. Tracer la bissectrice d'un angle BÂC

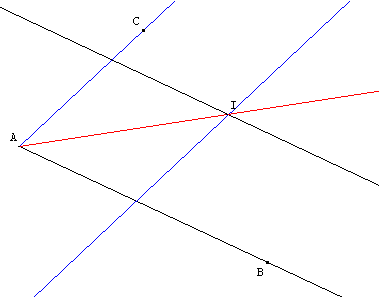
Placer la règle sur chaque côté de l'angle BAC.
Les deux droites tracées avec l’aube bord se coupent en I formant
un losange de diagonale [AI].

(AI) est donc la bissectrice de BÂC.

Télécharger la figure GéoPlan regle_bissectrice.g2w

Voir aussi : constructions de la bissectrice au compas

Bissectrice de deux droites ayant une intersection inaccessible

1.b. Médiatrice de [AB], milieu de [AB]

Soit [AB] un segment de longueur supérieure à la largeur de la règle.

Construction d'un losange de diagonale [AB] :
On incline la règle de telle façon que A et B soient situés chacun sur un bord de la règle.
Les deux couples de parallèles ainsi créés se rencontrent en C et D.
ACBD est un losange.
(CD) est la médiatrice de [AB].
[AB] coupe [CD] en son milieu

Cinquante problèmes pour les élèves de 4^ème et 3^ème : problème 23 de l'IREM de Lyon.

1.c. Deux tracés du milieu d'un segment

Comment peut-on construire le milieu du segment [AB] ?

La règle est supposée « aussi longue que nécessaire ».
Deux idées simples :
    – tracer un triangle de base [AB] et ses médianes ;

    – tracer un parallélogramme ACBD de diagonale [AB] :
la figure ci-dessus permet ainsi de trouver le milieu de [AB], intersection des deux diagonales du losange ACBD.

Télécharger la figure GéoPlan regle_losange.g2w

Pb 23 : cinquante problèmes 4^e-3^e

2. Partage d'un segment en parties égales

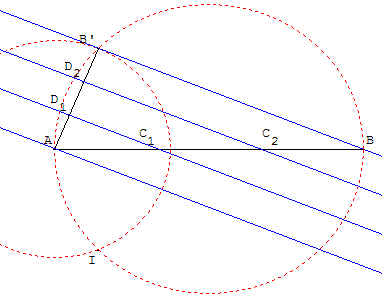
Cette méthode, plus théorique que pratique, permet de partager un segment de longueur supérieur à n fois la largeur de la règle. Dans la pratique, pour diviser le segment [AB], utiliser n règles identiques formant un réseau de droites parallèles et faire pivoter un des bords du réseau autour de A, jusqu'à ce que l'autre bord rencontre B.

Construction

Trouver B’ un des points d'intersection du cercle de diamètre [AB] et du cercle de centre A et de rayon égal à n fois la largeur de la règle.

Le réseau de parallèles à (BB’) partage [AB].

Télécharger la figure GéoPlan regle_diviser.g2w

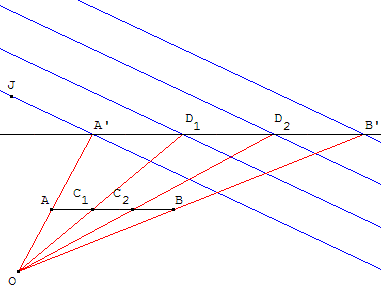
Lorsque le segment est trop petit, à partir d'un point A’,
tracer un faisceau de n + 1 parallèles qui partage [A’B’], parallèle à [AB], en n parties égales.
Rabattre la division à partir du point O, intersection de (AA’) et (BB’).

Télécharger la figure GéoPlan regle_petit_diviser.g2w

3. Milieu d'un segment a. Construction de Hilbert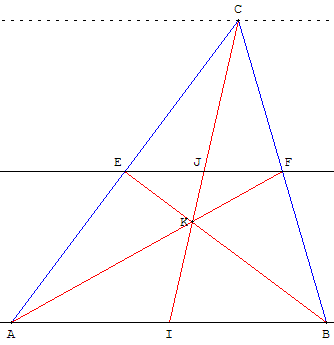 Grundlagen der Geometrie Avec une simple règle, sans compas on ne peut pas déterminer précisément le milieu d'un segment. Tout change si la règle non graduée est à bords parallèles. Elle permet alors non seulement de tracer une droite, mais aussi une parallèle à cette droite. Avec une règle à bords parallèles, comment est-il possible de construire le milieu d'un segment donné ? Pour construire le milieu, lorsque le segment est trop court, à défaut de la construction du losange, on a les constructions suivantes : Cas général : tracer une parallèle à [AB] et placer un point C (presque quelconque)   – Avec la règle à bords parallèles tracer une parallèle (d) à (AB)       et placer un point C à l'extérieur de ces deux droites.   – Mener deux sécantes (CA) et (CB) qui coupent (d) en E et F.   – Tracer (BE) et (AF) qui se coupent en K.   – Le point I, intersection de (AB) et (CK), est le milieu de [AB]. Cas particulier : tracer une parallèle à [AB] et placer un point C (tel que la distance de C à cette parallèle soit égale à la distance des deux droites : on a alors les trois médianes de ABC)   – Avec la règle à bords parallèles tracer une parallèle (d) à (AB), et une deuxième parallèle (d2) à (d).   – Le point C est placé sur cette deuxième parallèle.   – E et F sont alors les milieux de [AC] et [BC]. Les médianes (BE) et (AF) du triangle ABC se coupent en K son centre de gravité.   – La troisième médiane (CK) rencontre [AB] en son milieu I.

Télécharger la figure GéoPlan regle_milieu.g2w Construction du milieu, avec le compas seul Réciproque : construire une parallèle avec règle et milieu

Problème 23 de l'IREM de Lyon     Autre méthode : tracer un parallélogramme de diagonale [AB]. WikiPédia : construction du milieu d'un segment

3.b. Milieu d'une corde

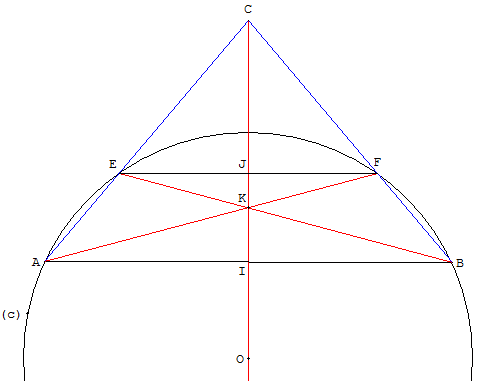
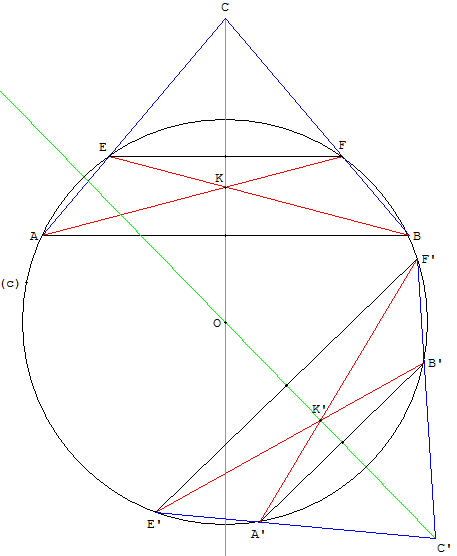
Trouver le milieu d'une corde [AB] d'un cercle suffisamment grand, avec une règle à bords parallèles.

  – Avec la règle à bords parallèles tracer une parallèle (d) à (AB).
  – Si la droite (d) coupe le cercle en deux points E et F et si les droites (AE) et (BF) se coupent en C ; réaliser la construction analogue à la figure ci-dessus.
  – Tracer les segments (BE) et (AF) qui se coupent en K.
  – La droite (CK) coupe [AB] en son milieu I.

J est aussi le milieu de la corde [EF].

Le centre du cercle est situé sur la droite (CK).

Télécharger la figure GéoPlan milieu_corde.g2w

4. Retrouver le centre d'un cercle

Comment trouver le centre d'un cercle sans compas : ?

Napoléon Bonaparte est censé avoir découvert comment à l'aide exclusive d'un compas, on pouvait retrouver le centre d'un cercle.
Comment trouver le même résultat avec une règle à bords parallèles ?

4.a. Configuration du milieu d'une corde

Réaliser deux fois la construction ci-contre de médiatrices :
le centre du cercle est à l'intersection des droites (CK) et (C’K’).

Télécharger la figure GéoPlan centre_cercle_corde.g2w

Voir aussi : retrouver le centre perdu avec les médiatrices de deux cordes

Construction du centre au « compas seul » : problème de Napoléon

Construction avec une équerre

4.b. Trouver un diamètre avec la configuration du losange

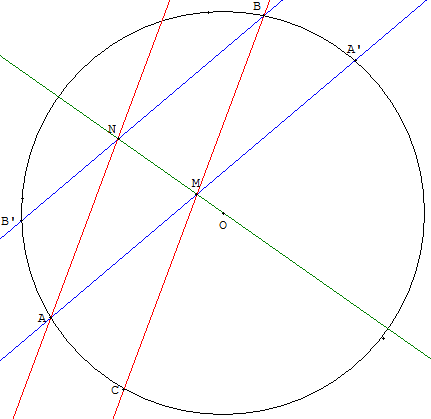
Comment tracer un diamètre avec une règle de largeur inférieure au diamètre du cercle ?

Solution

On place la règle sur le cercle et on trace les deux parallèles (en bleu) le long de ses deux bords. Le premier bord rencontre le cercle en A, le deuxième bord à l'opposé en B.

On déplace la règle et on fait pivoter le bord inférieur autour de B jusqu'à ce que le bord supérieur rencontre A. On trace (en rouge) les deux parallèles le long des bords de la règle.

Les points d'intersection M et N ainsi déterminés sont sur un diamètre du cercle (médiatrice de [AB]).

Télécharger la figure GéoPlan mon_079.g2w

4.c. Retrouver le centre avec la configuration du losange

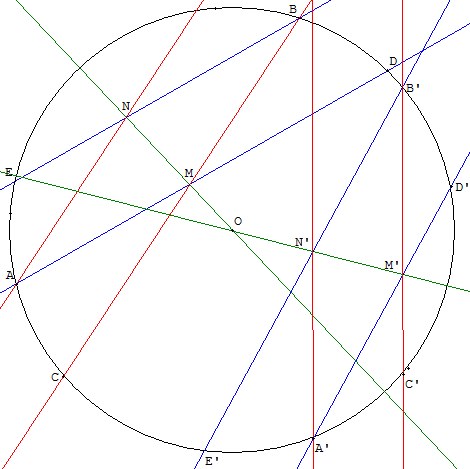
Comment retrouver le centre d'un cercle en traçant des losanges avec une règle à bords parallèles ?

Indication

Il suffit, comme ci-contre, de tracer deux diamètres (MN), puis (M’N’), pour obtenir le centre à leur intersection.

Télécharger la figure GéoPlan centre_cercle_losange.g2w

Comment trouver le centre d'un cercle sans compas :

Dessiner le centre perdu avec une équerre

Comment trouver le centre d'un cercle avec un compas :

Construction d'Euclide

Dessiner le centre perdu au « compas seul » : problème de Napoléon

5. Tiers d'un segment

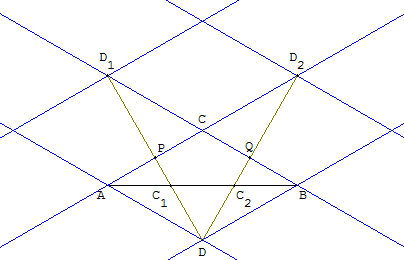
Comment réaliser un quadrillage de losanges

À l'aide de la règle, construire un réseau de losanges identiques, une diagonale d'un des losanges ayant pour sommets A et B.

En traçant les segments [DD₁] et [DD₂] reliant les sommets de ce réseau, on trouve les milieux P et Q des côtés du losange ACBD, et on en déduit les points C₁ et C₂ partageant le segment [AB] en trois parties égales.

On retrouve le partage en trois de la diagonale du parallélogramme ACBD par les droites (DD₁) et (DD₂) joignant D aux milieux des côtés opposés.

Télécharger la figure GéoPlan regle_diviser_3.g2w

Autres méthodes :

Pliage d'une feuille en trois parties égales : constructions - pliages en troisième

Tiers d'un segment avec la règle à bords parallèles

6. Parallèle à une droite

6.a. Deux parallélogrammes

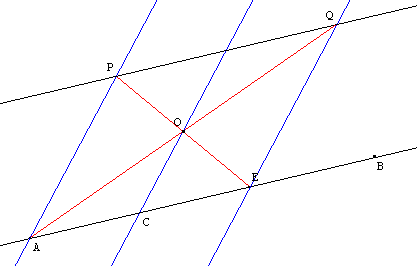
Pour tracer la parallèle à la droite (AB), passant par un point P, il suffit de tracer, avec la règle à bords parallèles, un faisceau de trois droites parallèles à (AP) qui coupent (AB) en A, C et E.

P, A et E sont les trois premiers sommets d'un parallélogramme de centre O, O intersection de la deuxième parallèle et de (PE).

La droite (AO) coupe la troisième parallèle en Q, quatrième sommet du parallélogramme.

La droite (PQ) est la parallèle à (AB) cherchée.

Télécharger la figure GéoPlan regle_parallele.g2w

6.b. Configuration de Desargues

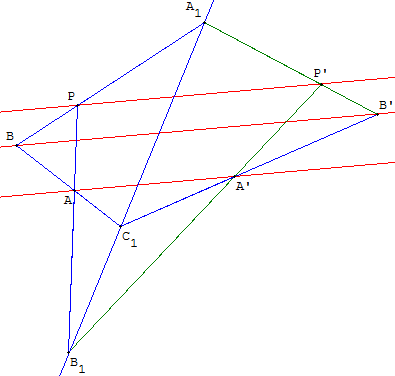
On se donne deux droites parallèles distinctes (d) et (d’), tracées avec une règle à bords parallèles et un point P extérieur de ces droites.

Tracer, avec la règle seule, la parallèle à la droite (d), passant par P.

Construction

Placer deux points A, A’ et B, B’ sur (d) et (d’). Les droites (AB) et (A’B’) se coupent en C₁.

Sur la droite (PA), placer un point B₁.

Les droites (BP) et (B₁C₁) se coupent en A₁.
Les droites (B₁A’) et (A₁B’) se coupent en P’.

La droite (PP’) est la parallèle à (d) cherchée.

Télécharger la figure GéoPlan desargues_para.g2w

c. construction à la règle seule d'une parallèle à deux droites parallèles : cette méthode s'utilise en traçant, avec le deuxième bord de la règle à bords parallèles placée le long de (AB), une parallèle (d’). Terminer comme indiqué dans l'article, la construction de la parallèle passant par le point donné P.

7. Symétrique d'un point par rapport à une droite

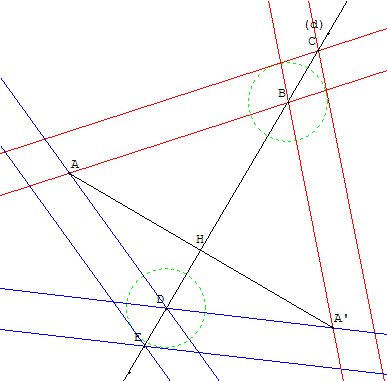
On donne une droite (d), un point A non situé sur (d),
construire le point A’ symétrique de A par rapport à (d), en utilisant la règle à bords parallèles.

Solution

Le point A sur un des bords de la règle, on trouve les points B et C intersections des bords de la règle avec (d). On retourne la règle de telle façon que B et C soient situés chacun sur l'autre bord de la règle. On obtient un tracé symétrique des deux positions de la règle en rouge avec un losange de diagonale [BC].

On recommence avec deux autres points D et E et obtient deux autres tracés en bleu où ces deux points sont sur les bords de la règle, en traçant le losange de diagonale [DE].

A’ est le symétrique de A : c'est l'intersection des droites (BA’) et (DA’) symétriques de (BA) et (DA) par rapport à (d).

Remarque : cette construction permet aussi de trouver la perpendiculaire abaissée du point A sur la droite (d) : la droite (AH).

Télécharger la figure GéoPlan regle_sym_point.g2w

Voir aussi : symétrique d'un point par rapport à une droite

8. Construction d'un triangle équilatéral avec deux cercles

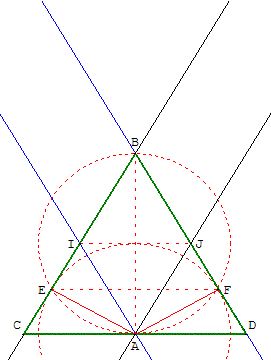
La règle à bords parallèles de largeur l permet de tracer un triangle équilatéral de hauteur AB = 2 l.

Tracer deux cercles de rayon l ; l'un de diamètre [AB] et l'autre de centre A. Ces deux cercles se coupent en E et F.

AE/AB = l/2l = ; c'est le sinus de l'angle ABE = 30°. L'angle EBF vaut 60°.

Les droites (BE) et (BF) et leurs parallèles, passant par A, forment un losange AIBJ.

En plaçant un bord de la règle sur [IJ], l'autre passe par A ou B. Pour A on obtient la perpendiculaire à (AB) qui coupe (BE) en C et (BF) en D.

BCD, ayant (AB) comme axe de symétrie et l'angle au sommet CBD de 60°, est un triangle équilatéral.

Télécharger la figure GéoPlan regle_equilateral.g2w

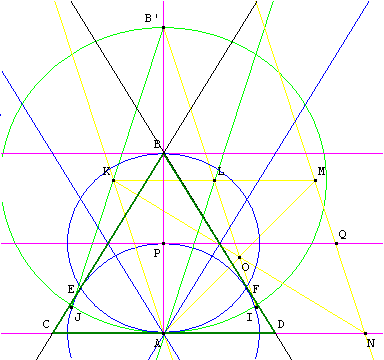
La règle à bords parallèles de largeur l permet la construction complète d'un triangle équilatéral d'axe (AB’).

Première étape : construction de la médiatrice (KL) de [AB’].
Comme ci-contre, tracer le cercle de diamètre [AB’] et le cercle c₂ de centre A et de rayon l ; ces cercles se coupent en I et J. Les bords de la règle placés sur A et (BI), puis sur (BJ) forment le losange AKB’L.

Deuxième étape : construction de (AN) parallèle à (KL) passant par A.
Comme au 2.3 avec la règle tracer la troisième parallèle à (KA) et (B’L) qui coupe (KL) en M. On complète le parallélogramme de sommets A, K, M et de centre O, par le quatrième point N.

Troisième étape : avec les bords de la règle construire les parallèles à (AN). Sur [AB’) on obtient les points P puis B tels que AP = l et PB = l.

Quatrième étape : terminer comme ci-contre.

Télécharger la figure GéoPlan regle_equilateral2.g2w

Voir : construction d'un triangle équilatéral par pliage d'une feuille rectangulaire

9. Pentagone régulier

Avec une règle à bords parallèles, il est possible de construire un pentagone régulier, voir mathafou.

En appliquant la méthode de Viète pour la trisection de l'angle,
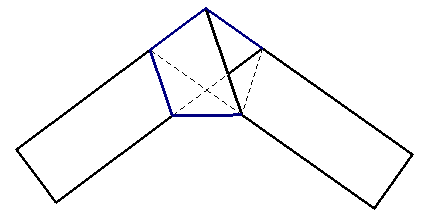
ci-dessous une construction avec quatre règles pivotant autour d'un sommet A en s'inspirant du pliage d'un nœud d'une bande.

Cette méthode de « coïncidence de points » qui s'inspire des « problèmes mécaniques du XVII^e » n'est pas une construction « à la règle et au compas ».

Les symétries sont difficiles à expliciter avec la règle, mais cette construction permet de visualiser les bandes, formées par quatre sommets consécutifs, articulées autour de losanges. Par exemple les bandes ABDE et ABCE, dessinant le losange ABA’E, sont les bandes passant de part et d'autre des points A et A’.

Construction du pentagone

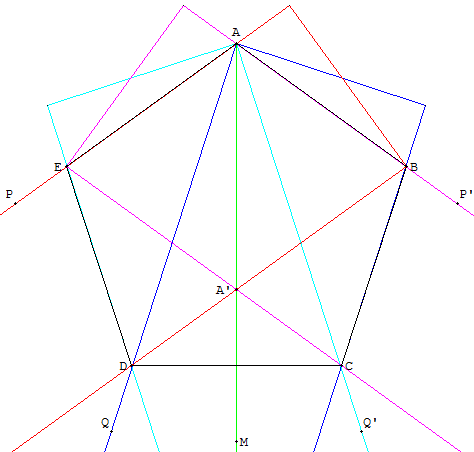
Construction à partir d'un sommet A et l'axe de symétrie (AM).

Choisir deux points P et Q (à l'extérieur de l'axe) et placer deux règles le long de (AP) et (AQ).

De façon symétrique, avec P’ et Q’ symétriques de P et Q par rapport à (AM), on place deux autres règles le long de (AP’) et (AQ’).

Il suffit ensuite de déplacer P et Q de telle façon que trois des règles soient concourantes en E d'une part et en D d'autre part.

Terminer le tracé avec le segment [CD]. ABCD est un pentagone régulier.

Télécharger la figure GéoPlan regle_pentagone.g2w

Constructions à la règle seule

Le point de concours de deux droites étant situé hors de la feuille, construire une droite passant par cette intersection inaccessible

Construction, avec la règle à bords parallèles, d'une bissectrice d'un angle de sommet inaccessible

Construction, à la règle et l'équerre, d'une perpendiculaire ou d'un carré passant par un point inaccessible

Construction au compas seul

Problèmes de construction au collège

Constructions à l'équerre

Tiers d'un segment

Mobile friendly