Descartes et les Mathématiques

Point inaccessible

Figures tronquées : constructions de géométrie, sans utiliser un point situé hors de la page.

Construire une droite passant par un point extérieur à la feuille

Deux droites concourantes se coupent en un point situé hors de la feuille (hors de l'écran). Dans cette page, on demande de faire des constructions sans utiliser ce point inaccessible.
Des situations à mettre en œuvre au collège en deux à trois heures suivant les niveaux et les objectifs.

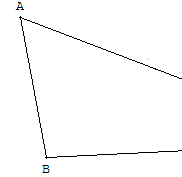
Par exemple, le sommet C d'un triangle ABC est en dehors de la feuille, construire malgré tout le centre de gravité et les médianes du triangle, la hauteur issue de C.

La grande supériorité de GéoPlan sur beaucoup de logiciels de géométrie est qu'il permet de concevoir des objets sans les visualiser.
      Avec GéoPlan, il est possible de créer le point d'intersection C des côtés, situé hors de l'écran, puis de tracer des droites passant par le pont C, sans y accéder.

Par contre avec Cabri, on devra faire des zooms arrière jusqu'à trouver le point C et revenir à la situation d'origine par des zooms avant.

1. Angle de deux droites

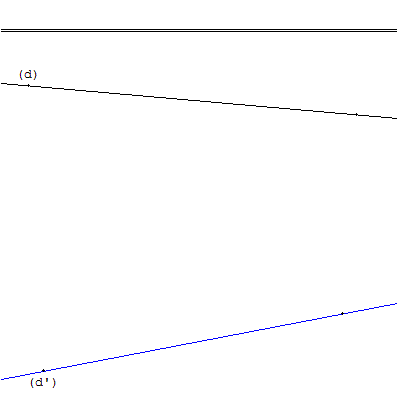
Détermination de l'angle de deux droites avec la symétrie centrale, accessible au collège dès la classe de cinquième.

Sachant que (d) et (d’) ne se coupent pas sur la feuille, comment déterminer l'angle des deux droites ?

Construction

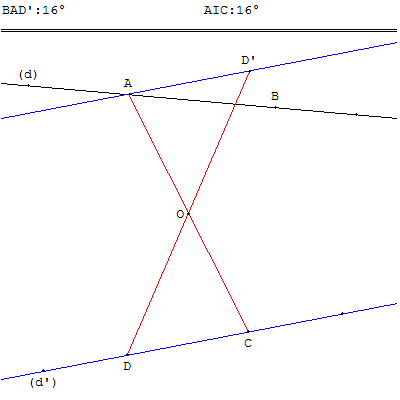
Placer des points A et B sur (d), C et D sur (d’).
Tracer le segment [AC], son milieu O et le point D’, symétrique de D par rapport à O.

La droite (AD’) est parallèle à (d’) et l'angle BÂD’ représente l'angle des droites (d) et (d’).

En effet, les angles alternes-internes BÂD’ et AÎD, par rapport à la sécante (AI), sont égaux.

Télécharger la figure GéoPlan angle_droites.g2w

Avec GéoPlan, il est possible de créer le point I d'intersection hors de l'écran :

I point d'intersection des droites d et d'

Commandes :
taper S pour afficher la solution.
taper A pour afficher l'angle des droites :

 Af1 affichage d'une mesure (en degré) de l'angle AIC

2. Tracer le symétrique d'un triangle

Symétrie centrale en classe de cinquième

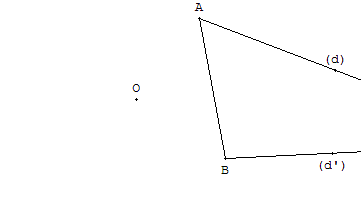
ABC est un triangle, mais le sommet C est en dehors de la feuille.
Construire, malgré tout, le symétrique du triangle ABC par rapport à O.

Télécharger la figure GéoPlan sym_triangle.g2w

Construction

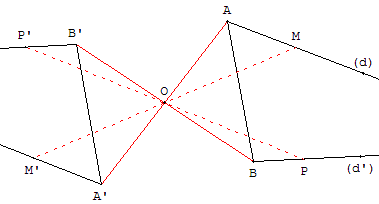
Placer deux points M sur (d) et P sur (d’), convenablement choisis, dont les images sont situées dans la feuille.
Les symétriques M’ et P’, de M et P par rapport à O, permettent de tracer les droites (A’M’) et (B’P’), symétriques de (d) et (d’).
Elles se coupent en C’ symétrique de C par rapport à O.

Bien que situés hors de l'écran, avec GéoPlan, il est possible de créer le point C, troisième sommet du triangle, et son symétrique C’.

3. Diagonale d'un parallélogramme

Classe de quatrième

Constructions dans un parallélogramme dont un sommet est inaccessible :
« en détachant précipitamment la feuille de son bloc, Pierre déchire une partie de son parallélogramme ; retrouver les diagonales ! »

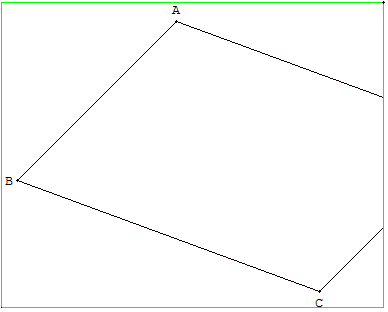
ABCD est un parallélogramme.
Seuls les points A, B, C sont situés sur la feuille.
Tracer la diagonale [BD] sans utiliser le point D.

Plus difficile

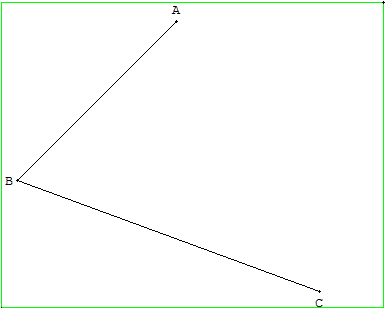
ABCD est un parallélogramme, D est une intersection inaccessible.
Seuls les points A, B, C et les segments [AB] et [BC] sont tracés.

Tracer la diagonale [BD] et les côtés [CD] et [AD], sans utiliser le point D.

Indications

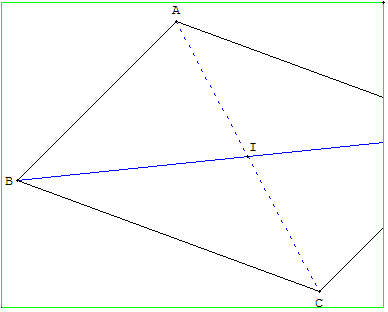
Tracer la diagonale [AC] et son milieu I.

La droite (BI) est la diagonale cherchée.

Télécharger la figure GéoPlan diag_para.g2w

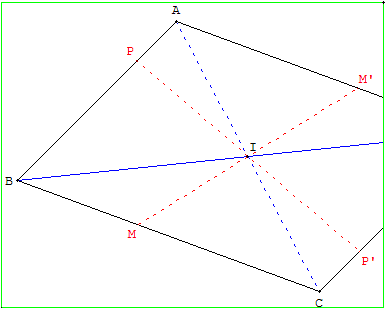
Comme ci-contre, tracer [AC], son milieu I et la diagonale [BD].

Utiliser la symétrie de centre I, pour tracer les côtés [CD] et [AD], en choisissant convenablement deux points sur [BA] et [BC] dont les images sont situées dans la feuille.

4. Bissectrice d'un angle inaccessible

Construction d'une bissectrice de l'angle de deux droites ayant une intersection inaccessible

Deux droites (d) et (d’) concourantes, inscrites sur une feuille, se coupent en un point I situé hors de la feuille, construire une bissectrice de (d, d’).

4.a. Bissectrices d'un triangle inaccessible

Comment tracer une bissectrice intérieure ou extérieure sans utiliser l'origine de l'angle

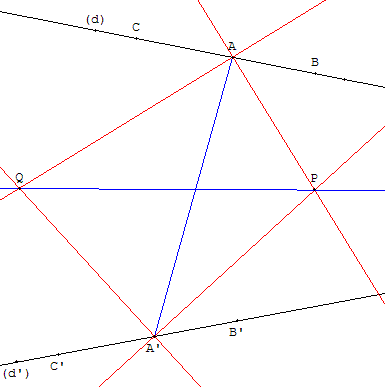
Placer deux points A sur (d) et A’ sur (d’).

Les bissectrices du triangle AA’I, issues de A et A’ se coupent en P, centre du cercle inscrit.

Les bissectrices extérieures du triangle AA’I, issues de A et A’ se coupent en Q, centre d'un cercle exinscrit.

La droite (PQ), troisième bissectrice intérieure du triangle AA’I est la bissectrice de (d) et (d’) cherchée.

Le tracé est possible lorsque les points P et Q sont situés sur la feuille.

Remarque technique :
GéoPlan permet uniquement de tracer les bissectrices d'un angle défini par trois points. Pour cela, on place les points B et C sur sur (d), puis B’ et C’ sur (d’) et on utilise des instructions comme :

d1 bissectrice de l'angle A’AB

Télécharger la figure GéoPlan bissectrice.g2w

4.b. Construction de deux parallèles équidistantes

Placer deux points M sur (d) et P sur (d’).

Sur la perpendiculaire en M à (d), reporter une longueur l et placer le point N à l'intérieur de l'angle des deux droites.
De même sur la perpendiculaire en P à (d’), placer le point Q.

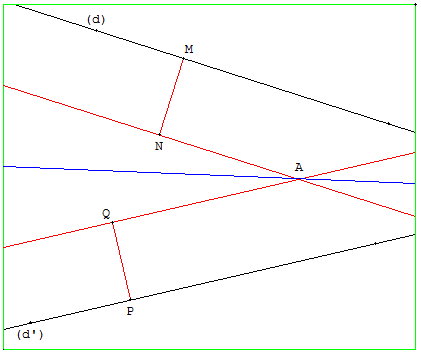
Par N, on trace la parallèle (d₁) à (d) et par D, on trace la parallèle (d₂) à (d’).

Lorsque l et les points M et P sont convenablement choisis, les deux parallèles sont sécantes en A.
Le point A, équidistant de (d) et (d’), est situé sur la bissectrice cherchée.

Ensuite, il suffit de tracer la bissectrice de (d₁) et (d₂), qui est la bissectrice de (d) et (d’) cherchée, passant par I.

Télécharger la figure GéoPlan bissectrice_2_para.g2w

Remarque : cette figure correspond à la construction de la bissectrice avec une règle à deux bords parallèles

Variante : il est aussi possible de tracer un deuxième point d'intersection B, avec deux autres parallèles.
Voir la figure ci-dessous.

4.c. Règle à bords parallèles

Tracer deux paires de droites parallèles aux droites données (d) et (d’) situées à des distances égales de ces mêmes droites.

Construction

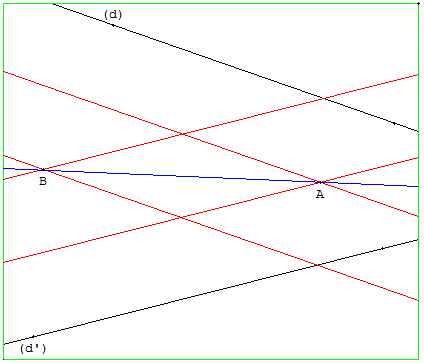
Cette construction se fait facilement avec une règle à bords parallèles de taille convenable.

Dans le réseau de losanges ainsi formé, on place les sommets opposés A et B d'un losange.

La droite (AB) est la bissectrice cherchée.

Télécharger la figure GéoPlan bissectrice_para.g2w

4.d. Pliage

(d) et (d’) étant inscrites sur une feuille, amener (d) en coïncidence avec (d’), la trace du pli donne la bissectrice.

Construction par pliage de la droite passant par un point M et par l'intersection inaccessible de deux droites (d) et (d’)
Les pliages permettent de résoudre le problème dans le cas où M est entre (d) et (d’) :
Le pliage donne une droite (d₃). Si M est entre (d) et (d₃) on recommence en amenant (d) sur (d₃) pour obtenir un pli (d₄), et ainsi de suite en rabattant l'une sur l'autre les deux droites entre lesquelles le point M est situé… Au bout de 5 ou 6 pliages maxima, la position de droite (IM) sera connue au millimètre près.

5. Perpendiculaire

Classe de sixième

Tracés à la règle et à l'équerre.

Tracer la perpendiculaire à une droite lorsque le point de concours n'est pas sur la feuille.

Tracer la droite passant par A, perpendiculaire à la droite (PQ).
Le tracé se fera avec une règle et une équerre (non graduées).

On se limite aux tracés à l'intérieur de l'écran et on s'interdit les zooms.
Avec GéoPlan, on n'utilisera pas la commande :
créer > droite perpendiculaire passant par A.

Télécharger la figure GéoPlan perpendiculaire.g2w

Solution à la règle et à l'équerre

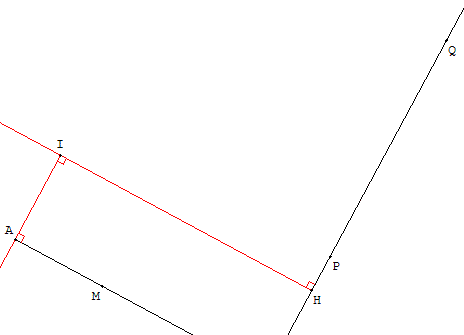
Placer l'équerre le long de la droite (PQ), le sommet de l'angle droit en un point H et tracer une droite (HI) perpendiculaire à (PQ).

Placer ensuite un des petits côtés de l'équerre sur cette perpendiculaire et la faire glisser, jusqu'à ce que l'autre petit côté passe par A.
Tracer la perpendiculaire (IA).

Enfin, tracer la droite (AM), perpendiculaire en A à (IA).
Cette droite est la solution perpendiculaire à (PQ).

5.b. Tracé d'un carré avec deux sommets inaccessibles

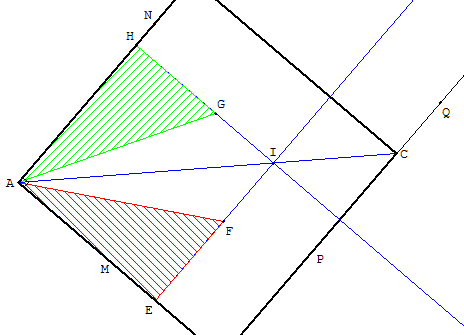
Construire, à l'équerre, un carré de sommet A, ayant un côté situé sur la droite (PQ)

Le point A et la droite (PQ) sont situés de telle façon que le sommet C sera le seul autre sommet du carré ABCD situé sur la feuille, les sommets B et D ne seront pas dessinés.

Tracer, comme ci-dessus, la droite (AM) passant par A, perpendiculaire à (PQ),
puis en plaçant l'angle droit de l'équerre en A, tracer la perpendiculaire (AN), droite parallèle à (PQ).
Placer un des coins de l'équerre en A, un des petits côtés [AE] sur (AM) et tracer une perpendiculaire [EF) à (AM).
Retourner l'équerre, ce même petit côté sur (AN), tracer une deuxième perpendiculaire [HG) à (AN).
Ces deux perpendiculaires se coupent en I et font apparaître un petit carré AEIH, de diagonale [AI].

La droite (AI), diagonale du carré cherché, coupe (PQ) en C sommet de ce carré.
La perpendiculaire en C à (PQ) est le dernier côté du carré ABCD.

Télécharger la figure GéoPlan carre1.g2w

Retrouver cette construction dans : tracé du carré à la règle et l'équerre

5.c. Autre tracé à la règle et à l'équerre

Avec une équerre, qui n'est pas isocèle, il est possible de tracer, comme ci-dessus, la droite (AM) passant par A, perpendiculaire à (PQ).
Placer l'angle droit de l'équerre en A, tracer la perpendiculaire (AN) et marquer l'hypoténuse [EF] sur la feuille.

Retourner l'équerre, en permutant les petits côtés, faire un deuxième tracé de l'hypoténuse [GH].

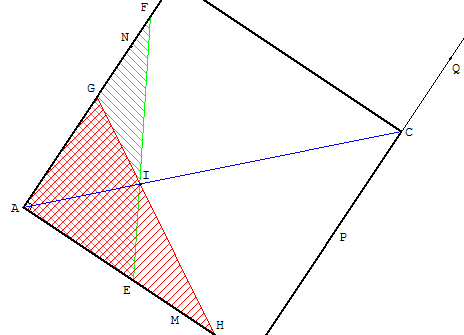
Ces deux droites (EF) et (GH) se coupent en I et la droite (AI) est la bissectrice de MAN. Les angles MAI et NAI mesurent 45° et (AI) est une diagonale du carré.

Comme ci-contre on construit le sommet C du carré, intersection de (AI) et (PQ),
et en plaçant l'angle droit de l'équerre en C, la perpendiculaire tracée est le dernier côté du carré.

Télécharger la figure GéoPlan carre2.g2w

Retrouver cette construction dans : autre tracé du carré à la règle et l'équerre

5.d. Axes de symétrie

Classe de sixième

Sans prolonger les côtés de la figure hors du cadre, tracer tous les axes de symétrie du carré.

Indications : tracer un des axes de symétrie : dans cette figure la diagonale (AC).
Placer le centre de symétrie O, milieu de [AC].
Tracer la deuxième diagonale perpendiculaire en O à (AC).
Terminer avec les deux médianes du carré, perpendiculaires aux côtés, passant par O.

6. Triangle tronqué

Centre de gravité d'un triangle tronqué

Tracer les médianes

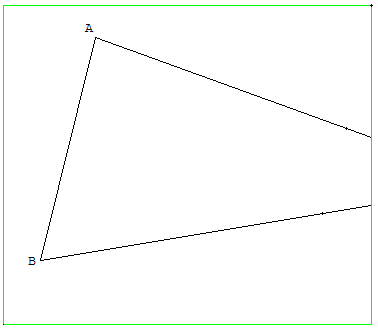
ABC est un triangle dont le sommet C est inaccessible
Tracer le centre de gravité G de ce triangle.

Télécharger la figure GéoPlan centre_gravite.g2w

Variante

Pour un triangle tronqué, tracer le cercle circonscrit et son centre en utilisant la construction des milieux A’ et B’ ci-contre.

Droites des milieux

Indications

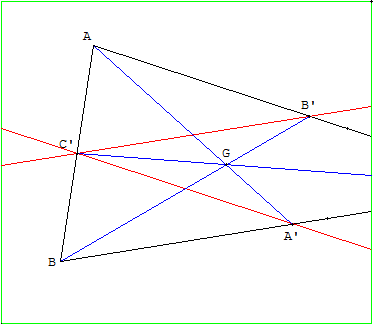
Tracer le milieu C’ du segment [AB].

Tracer les parallèles aux côtés (AC) et (BC), passant par C’.
Ces parallèles coupent [AC] en son milieu B’ et coupe [BC] en son milieu A’.

Si les points A’ et B’ sont situés dans l'écran, il est possible tracer les médianes [BB’] et [CC’].
Leur intersection est le centre de gravité G.

La droite (C’G) est la troisième médiane qui passe par le sommet inaccessible C.

Remarque

Cette construction demande que les milieux A’, B’ et C’ soient situés dans l'écran.
Elle est facile avec un triangle dont il manque un seul sommet.

Avec cette condition, il est encore possible de trouver le centre de gravité d'un triangle dont il manque deux sommets :
Si le point A est situé dans l'écran, il suffit de tracer la droite des milieux (B’C’) comme droite parallèle au côté (BC), située à mi-distance entre ce côté et A.
Tracer la droite des milieux (A’C’) comme droite parallèle au côté (AC), passant par C’.
G, aux deux tiers de la médiane [AA’], peut être tracé avec la médiane (CC’) qui passe par le milieu de [B’C’].

Périmètre du triangle tronqué

Déterminer le périmètre du triangle ABC.

Indication : il suffit de tracer, dans le cadre, un triangle semblable : par exemple ici, doubler le périmètre du triangle moitié AB’C’.

Table des matières