Descartes et les Mathématiques
Calculs d'aire - Théorème de Pick
Des images aux formules : calcul de l'aire d'un polygone.
Sommaire
1. Aire d'un triangle à l'intérieur d'un parallélogramme
La planche à clous comme géoplan
Parabole dans un géoplan 5 × 5
Le théorème de Pick donne une formule pour calculer l'aire d'un polygone sur une grille du plan,.avec le nombre i de points intérieurs au polygone et du nombre b de points sur le bord du polygone :
.S = i + b/2 - 1
1. Aire d'un triangle à l'intérieur d'un parallélogramme
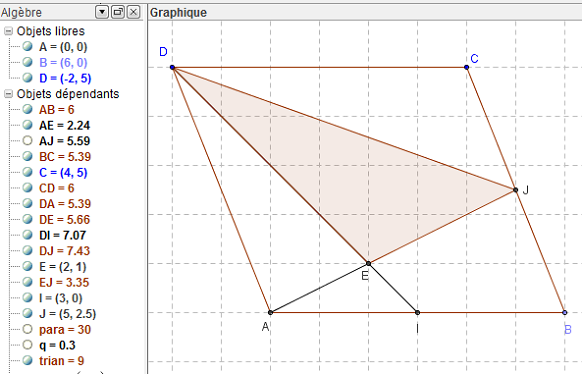
ABCD est un parallélogramme ; soit I le milieu de [AB] et J le milieu de [AB]. les droites (AJ) et (DI) se coupent en E
Quelle fraction de l'aire du parallélogramme représente l'aire du triangle DEJ ?
Ayant réalisé une figure avec GeoGebra, on peut calculer le rapport :
q = 
= Aire[trian]/ Aire[para] = 
.
En déplaçant les points A, B ou D, on remarque que le résultat est indépendant du parallélogramme.
En effet, le quotient d'aire est une propriété affine qui se conserve par ces déplacements.
On peut donc travailler avec des parallélogrammes particuliers, où les points sont placés sur le quadrillage ; comme le parallélogramme ci-dessus de côté AB = 6 et de hauteur 5 ; ici le point E est aussi un point du quadrillage.
Figure interactive dans GeoGebraTube : triangle construit dans un parallélogramme
2. Calculs d'aire
2.a. Calcul de l'aire du triangle DEJ
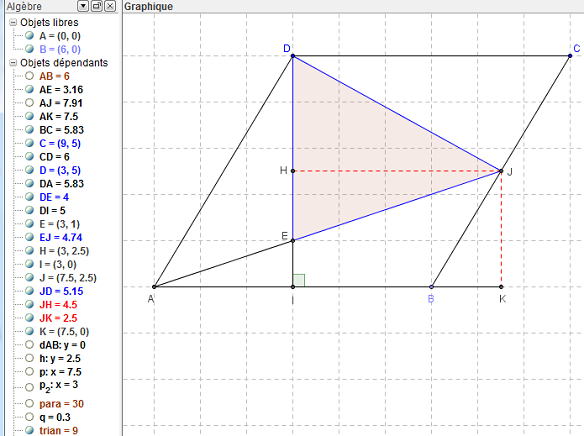
Il est possible de calculer dans le parallélogramme ci-dessus où le sommet D se projette en I,
avec AB = 6 et DI = 5.
Dans le repère d'origine A, les coordonnées sont B(6, 0) et D(3, 5).
E et J ont alors pour coordonnées sont E(3, 1) et J(7,5 ; 2,5).
J se projette sur (DI) en H(3 ; 2,5).
Aire(ABCD) = Aire[para]
= AB × DI = 6 × 5 = 30.
Aire(DEJ) = Aire[trian]
= 
DE × HJ = × 4 × 4,5 = 9.
On retrouve le rapport
q = = .
Figure interactive dans GeoGebraTube : aire d'un triangle dans un parallélogramme
2.b. Autre calcul : la propriété des proportions
Le triangle DAJ a une aire égale à la moitié de celle du parallélogramme.
Le rapport des aires des triangles DAJ et DEJ est égal au rapport de leurs bases 
.
Ce rapport se calcule facilement avec Thalès dans le triangle AKJ, avec la parallèle (IE).
= 
= 
, donc 
= et = × = .
3. Théorème de Pick (1899)
Georg Pick 1859-1942
Figure interactive dans GeoGebraTube : théorème de Pick
Soit un polygone non croisé, construit sur une grille de points équidistants, tel que tous ses sommets soient des points de la grille ; le théorème de Pick fournit une formule simple pour calculer l'aire S de ce polygone, en se servant du nombre i de points de la grille à l'intérieur du polygone et du nombre b de points sur le bord du polygone :
S = i + b – 1.
Cette formule simple peut être utilisée par des enfants de l'école élémentaire, en dessinant des polygones dont les sommets sont sur un quadrillage, ou en étirant des élastiques sur un planche à clous.
3.a. Calcul de l'aire du triangle DEJ
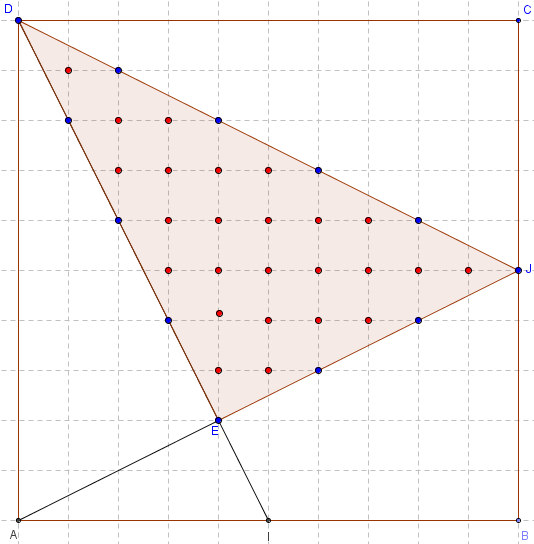
Il est possible de réaliser la figure dans un carré 10 × 10.
Il y a 25 points à l'intérieur du triangle et 12 points sur les côtés du triangle.
On a donc S = 25 + × 12 – 1 = 30.
On a encore le rapport q = = 
=
3.b. La propriété des proportions
On visualise sur cette figure le rapport = des bases des triangles DAJ et DEJ et on a bien = .
On pourrait aussi vérifier que :
Aire(AED) = × AD × hauteur = × 10 × 4 = 20
et Aire(DEJ) = Aire(ADJ) – Aire(AED) = 50 – 20 = 30.
WikiPédia : Théorème de Pick
Dans d'autres pages du site
Collège :
Calcul d'aires
Aires du parallélogramme et du trapèze
Aire d'un triangle inscrit dans un carré
Démonstrations avec la méthode des aires :
théorème de Thalès
théorème de Pythagore
Triangles en seconde :
Multiplication de l'aire d'un triangle,
Google friendly
|
. |
Page no 195, réalisée le 8/11/2012 |