Calculs et découpage d'aires - Angles avec la géométrie dynamique
Des idées de situations pour faire et enseigner des mathématiques avec un logiciel de géométrie dynamique.
…Calculs d'aire – Formulaire
Aire maximale d'un triangle
Aires au collège
Calculs d'aires par découpage
Quadrilatère orthodiagonal, cerf-volant
Multiplication de l'aire d'un parallélogramme
Aires au lycée en seconde
Multiplication de l'aire d'un triangle
Aire formée par deux segments circulaires
Calculs d'aires dans un rectangle
Calcul de π dans le papyrus de Rhind : fractions égyptiennes
Optimisation : aire entre deux triangles équilatéraux
GeoGebraBook
Calculs et découpage d'aires
Méthode des aires : démonstration utilisant la propriété d'Euclide : « les triangles qui ont la même hauteur sont l'un relativement à l'autre comme leurs bases ».
Démonstrations avec la méthode des aires :
théorème de Thalès
théorème de Pythagore
Calcul de l'aire d'un quadrilatère non convexe :
prenons de la hauteur
Transformer un quadrilatère en triangle de même aire - Olympiades 2008
Classe de première
Calcul d'aire minimum : minimum-maximum
Analyse en option 1ère L - TL
Un partage équitable - Olympiades 2008
Terminale S : calculs d'aires et de volumes
Intégration par la méthode des rectangles ou des trapèzes
Calculs du volume d'une cuve
Avec GeoGebra au collège
Avec GeoGebra au lycée
Optimisation d'aires en seconde
Aire minimale d'un triangle inscrit dans un rectangle
Géométrie du triangle
Angles au collège
Angles-Trigo (hors programme)
Angles Rotations
Culture
mathématique
WikiVersity
Calculs d'aire - Formulaire
L'aire est une mesure de grandeur des figures du plan ou des surfaces de l'espace. La figure de base pour le calcul d'une aire est le carré unité, de côté 1.
Quadrature : construire, à la « règle et au compas », un carré d'aire égale à celle d'une figure donnée.
Triangle
L'aire d'un triangle a pour mesure le demi-produit d'un côté par la hauteur perpendiculaire à ce côté.
Aire(ABC) = 
base × hauteur b × h = AC × BH avec la base BC = b et la hauteur issue de A : AH= h.
Comme h = AB sin A = c sin A, on a aussi Aire(ABC) = bc sin A.
Formule de Héron d'Alexandrie en fonction des longueurs des trois côtés :
p = (a + b + c) désigne le demi-périmètre : Aire(ABC) = 
.
Formule des aires : Aire(ABC) = S = pr et r = 
= 
où r est le rayon du cercle inscrit.
GéoPlan calcule directement l'aire du triangle avec le menu : « Créer>Numérique>Calcul géométrique>Aire d'un triangle ».
Triangles particuliers : aire d'un triangle rectangle,
l'aire d'un triangle équilatéral de côté a est 
a2 ;
quadrature du triangle équilatéral
Quadrilatères particuliers
Carré : l'aire du carré de côté a est a2.
Rectangle : l'aire du rectangle de longueur L et de largeur l est égale au produit Ll.
Quadrature du rectangle
Parallélogramme : l'aire d'un parallélogramme a pour mesure le produit de la base par la hauteur,
ou bien l'aire d'un parallélogramme est aussi égale au double de l'aire d'un des triangles, formé par une diagonale et les deux côtés consécutifs correspondants.
Losange : l'aire d'un losange a pour mesure le produit de la base par la hauteur
ou bien l'aire est aussi égale à la moitié du produit des longueurs des diagonales.
Trapèze : l'aire d'un trapèze est le produit de la moyenne des bases par sa hauteur.
Quadrilatère croisé : le décomposer en deux triangles de part et d'autre du point d'intersection des côtés.
Quadrilatère et diagonales : L'aire d'un quadrilatère convexe est égale au demi-produit des diagonales multiplié par le sinus de l'angle qu'elles forment.
Cerf-volant : l'aire d'un cerf-volant (géométrie) est égale à la moitié du produit des longueurs des diagonales.
Quadrilatère orthodiagonal : l'aire d'un quadrilatère orthodiagonal, non croisé, est égale au demi-produit des longueurs des diagonales.
Quadrilatère convexe quelconque : le décomposer en deux triangles le long d'une des diagonales, ou bien transformer ce quadrilatère en un triangle.
Polygone convexe
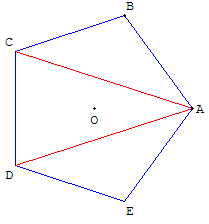
Pour calculer l'aire d'un polygone convexe, le découper en triangles, ou bien transformer ce polygone en triangle.
Pentagone :
calcul de l'aire du pentagone par découpage : faire la somme des aires des trois triangles ci-contre.
Voir la quadrature du pentagone
Cercle
Cercle : l'aire du disque de rayon r est πr2.
Secteur circulaire : surface du disque comprise entre deux rayons.
Calcul de l'aire d'un secteur circulaire : multiplier la moitié de l'angle (exprimé en radian) par le carré du rayon :
si OAB = α, l'aire du secteur est 
.
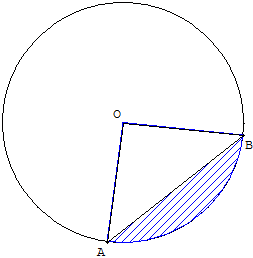
Segment circulaire (segment de cercle, parfois appelé lunule) : figure mixtiligne comprise entre l'arc de cercle AB et la corde [AB] qui le sous-tend.
Calcul de l'aire d'un segment de cercle :
l'aire du segment circulaire AB, sur un cercle de centre O, est celle du secteur circulaire compris entre les demi-droites [OA), [OB) et l'arc AB à laquelle selon les cas, on ajoute ou on retranche l'aire du triangle OAB.
Quadrature de la parabole par la méthode d'Archimède
Lien colle maths ts : problème de minimum ouvert :
On se demande pour quelle valeur de l'ouverture l'aire du triangle est égale à celle de la surface comprise entre la droite (AB) et le cercle.
Aire maximale d'un triangle
GéoPlan permet la mise en place de situations qui pourraient paraître complexes, mais auxquelles la dynamique de la figure permet de donner du sens. Certains de ces exercices seront alors abordables au collège en classe de troisième.
Utilisation du logiciel gratuit GéoPlan pour une recherche
Dans ces exercices est utilisée la technique GéoPlan d'une seule figure avec deux cadres : un cadre pour le triangle, un cadre pour la fonction représentative de l'aire.
La recherche d'un triangle d'aire maximale se fait en deux étapes.
Dans un premier temps, en déplaçant un des sommets du triangle, on trouve, en général, une première condition d'optimisation du problème, assez fréquemment un triangle isocèle.
On validera cette hypothèse par une méthode analytique (maximum de fonction lu graphiquement avec GéoPlan ou calculé avec une dérivée) ou par des considérations géométriques.
Dans un deuxième moment, on reprend la figure assujettie à cette hypothèse et on recommence la recherche avec deux points fixes et un point variable.
Souvent l'énoncé proposera d'emblée cette situation avec un seul point mobile.
Triangle d'aire maximale
Aire maximale d'un triangle inscrit dans un carré
Triangle inscrit dans un rectangle :
pliage du coin d'une feuille, un devoir qui ne fait pas un pli !
Aire maximale d'un triangle isocèle inscrit dans un cercle
Aire maximum d'un triangle de périmètre fixé :
optimisation en troisième
aire maximale d'un triangle isocèle à l'épreuve pratique de TS
Rectangle d'aire maximale
Aire maximale d'un rectangle inscrit dans un triangle rectangle - démonstration par l'étude d'une parabole - démonstration géométrique
Aire maximale d'un rectangle inscrit dans un trapèze
Le plus grand rectangle inscrit dans un triangle isocèle
Carré d'aire maximale, voir : olympiades Versailles 2005
Calculs de volume de polyèdres
Le volume d'un solide de l'espace est sa mesure. L'unité de volume n'apparaît pas dans les formules. Elle est implicitement donnée par le volume du cube unité.
Cubature : transformation d'un solide en un cube de même volume.
Volume du cube de côté a : V = a3.
Volume d'un parallélépipède rectangle : Volume(ABCDEFGH) = Aire de la base × hauteur = Aire(ABCD) × AE = AB × AD × AE.
Volume d'un prisme droit : Aire de la base × hauteur = B × h.
Volume d'un cylindre : Aire de la base × hauteur = B × h.
Volume d'une pyramide (d'un tétraèdre ou d'un cône) : V = 
× aire de la base × hauteur = × Abase × h.
Volume d'un tétraèdre régulier : V = × Abase× h = a2 × 
a = 
a3.
Volume d'un tronc de pyramide (ou d'un tronc de cône) : un tronc de grande base B, de petite base b et de hauteur h, a pour volume V = 
[B + b + 
].
Page créée le 9/10/2009,
modifiée le 12/5/2010