René Descartes Descartes et les Mathématiques

La géométrie du triangle V

Relations métriques dans le triangle

Sommaire

1. Inégalités triangulaires
Théorème d'Al-Kashi

2. Somme des angles d'un triangle

3. Loi des sinus

4. Formule de Héron d'Alexandrie

5. Formule des aires

6. Cercles inscrit et exinscrit - Distances entre les sommets et les points de contact

Relation d'Euler (théorème d'Euler)

7. Théorème japonais de Carnot

Soit ABC un triangle tel que BC = a, AC = b et AB = c ; p = (a + b + c) désigne le demi-périmètre.
On note Â, et les angles du triangle.

1. Inégalités triangulaires

|b − c| < a < b + c

Les inégalités sont strictes pour un triangle non aplati.
Réciproquement, lorsque l'on a une égalité, les points A, B et C sont alignés.

Théorème d'Al-Kashi

geometrie du triangle - triangle quelconque - copyright Patrice Debart 2012

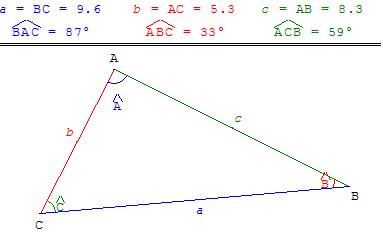
Télécharger la figure GéoPlan tri_quel.g2w

Formules de Pythagore généralisées dans le triangle quelconque :

geometrie du triangle - angles d'un triangle quelconque - copyright Patrice Debart 2012

a² = b² + c² − 2 b c cos(Â),
b² = a² + c² − 2 a c cos(B),
c² = a² + b² − 2 a b cos(C).

Avec ces formules on peut calculer les cosinus des angles du triangle à partir des longueurs des côtés a, b, c.
Par exemple, cos C = .

Télécharger la figure GéoPlan tri_quel2.g2w

2. Somme des angles d'un triangle

La somme des angles géométriques d'un triangle est un angle plat :

+ + = 180°.

L'angle extérieur d'un triangle est égal à la somme des deux angles intérieurs non adjacents.

Démonstration et figures, en classe de cinquième, voir : triangle au collège ; construction par pliage

Télécharger la figure GéoPlan somme_angles.g2w

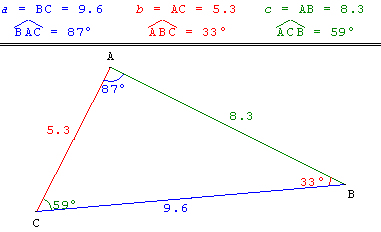
Problème d'arrondi

Avec les angles BAC = 87°, ABC = 33°, ACB = 59°, la somme de ces angles est égale à 179°. Plus haut, il est dit que la somme des angles d'un triangle est égale à 180° ?

Les calculs étant faits « au degré près », GéoPlan arrondit les trois angles par défaut et on perd un degré pour l'arrondi de la somme.
Avec un calcul au dixième les angles BAC = 87,5°, ABC = 33,5° sont arrondis par excès et ACB = 59,0° par défaut : la somme est bien arrondie à 180,0°.

3. Loi des sinus

S est l'aire du triangle ABC, R est le rayon du cercle circonscrit à ABC :

= = = = 2R,

d'où abc = 4RS.

4. Formule de Héron d'Alexandrie (60 ap. J.-C.)

Aire du triangle en fonction des longueurs des trois côtés.

p = (a + b + c) désigne le demi-périmètre.

S =

Cette formule aurait été connue d'Archimède. Dans son traité « sur le dioptre », Héron en donne la plus ancienne démonstration connue.

Formule de l'aire d'un triangle avec la hauteur

L'aire d'un triangle a pour mesure le demi-produit d'un côté par la hauteur perpendiculaire à ce côté.

S = base × hauteur.

Calcul des hauteurs du triangle

Si h_A, h_B, h_C sont les longueurs des trois hauteurs d'un triangle ABC, des calculs des aires ci-dessus S = a h_A = b h_B = c h_C,
on tire h_A = = , h_B = = …, h_C = = …

5. Formule des aires

Cercle inscrit

Les trois bissectrices (At_A), (Bt_B), (Ct_C) d'un triangle ABC sont concourantes en I, centre du cercle inscrit (c).

Soit r le rayon du cercle inscrit.

Le cercle (c) est tangent aux côtés du triangle en i_A, i_B et i_C.

Le triangle ABC est décomposable en trois triangles IBC, ICA, IAB,
de sommet I et de hauteurs Ii_A, Ii_B, Ii_C; de même longueur r.

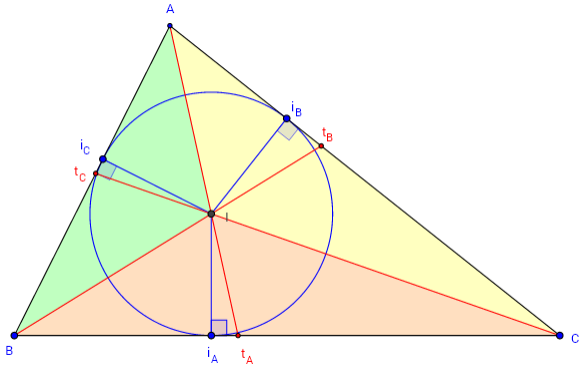
Formule des aires

L'aire S du triangle ABC est donc :

S = Aire(IBC) + Aire(IAC) + Aire(IAB)

S = ar + br + cr
= (a + b + c) × r = p × r.

Donc S = pr et r = = .

Avec la formule de Héron on a : r = = .

Avec la formule de l'aire du triangle S = bc sin A,
on trouve que le rayon du cercle inscrit est r = = .

Figure interactive dans GeoGebraTube : formule des aires

Cercle exinscrit

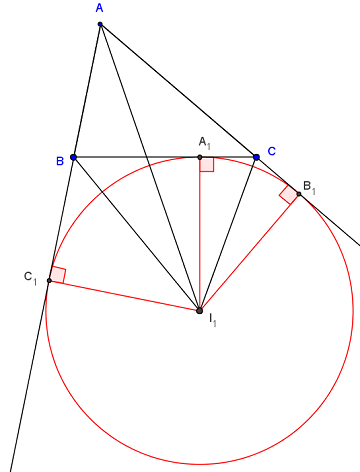
Soit I₁ le centre du cercle exinscrit dans l'angle BÂC du triangle et r₁ son rayon.
L'aire du triangle ABC est décomposable avec trois aires : la somme des aires des triangles I₁AB, et I₁CA moins l'aire de I₁BC,
de sommet I₁ et de hauteurs I₁C₁, I₁A₁, I₁B₁ de même longueur r₁.

S = A(I₁CA) + A(I₁AB) – A( I₁BC).

L'aire du triangle ABC est donc
S = br₁ + cr₁ – ar₁ = (b + c – a) × r₁ = (p – a) × r₁.

Donc S = (p – a) r₁.

On trouverait de même pour les deux autres cercles exinscrits :
S = (p – b) r₂ pour le cercle de rayon r₂ exinscrit dans l'angle B,
S = (p – c) r₃ pour le cercle de rayon r₃ exinscrit dans l'angle C.

Figure interactive dans GeoGebraTube : cercle exinscrit du triangle

6. Cercles inscrit et exinscrit

Distances entre les sommets et les points de contact

Cercle inscrit
Longueurs des segments

AB₁ = AC₁ = p – a = (– a + b + c),
BA₁ = BC₁ = p – b = (a – b + c),
CA₁ = CB₁ = p – c = (a + b – c).

geometrie du triangle - cercle inscrit - figure Geogebra - copyright Patrice Debart 2012

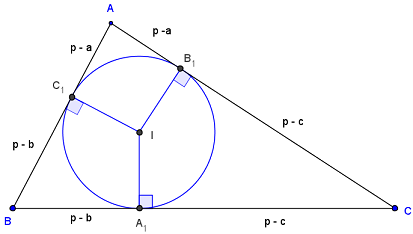
Preuve

En effet, pour chacun des sommets, les deux tangentes sont de longueurs égales :
AB₁ = AC₁ ; ainsi que BA₁ = BC₁ et CA₁ = CB₁.

Avec AB₁ + AC₁ + BA₁ + BC₁ + CA₁ + CB₁ = 2p,
on a AB₁ + BA₁ + CA₁ = p, soit AB₁ + a = p et AB₁ = p – a.

Figure interactive dans GeoGebraTube : cercle inscrit dans un triangle et distances

Voir cas particulier du triangle rectangle

Voir points de Gergonne et de Nagel

milieux des segments joignant les centres des cercles inscrit et exinscrits

Cercles inscrit et exinscrit

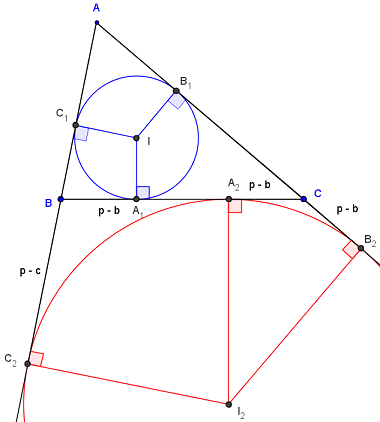
BA₂ = BC₂ = p – c,
CA₂ = CB₂ = p – b.

En effet, 2p = b + c + BA₂ + CA₂ = AC₂ + AB₂,
avec AC₂ = AB₂ = p.

On peut en déduire que B₁B₂ = B₁C + CB₂ = (p – c) + (p – b) = a = BC.
On a donc B₁B₂ = C₁C₂ = BC.

On a vu ci-contre que BA₁ = p – b ; les points A₁ et A₂ sont symétriques par rapport au milieu C’ de [AB].

Figure interactive dans GeoGebraTube : cercles inscrit et exinscrit du triangle

Relation d'Euler (théorème d'Euler)

Distance entre les centres des cercles inscrit et circonscrits

Si le cercle circonscrit d'un triangle a pour centre O et pour rayon R et le cercle inscrit a pour centre I et pour rayon r, la relation d'Euler permet de calculer le carré de la distance des deux centres :

OI² = R² – 2Rr.

Si d = OI alors d² = R(R – 2r).

Démonstration : voir la puissance du point I par rapport au cercle circonscrit (c) et un cercle (Γ).

Voir : quatre relations d'Euler

Théorème de Steiner−Lehman

Si deux bissectrices d'un triangle ont même longueur, le triangle est isocèle.

7. Théorème japonais de Carnot - angles aigus

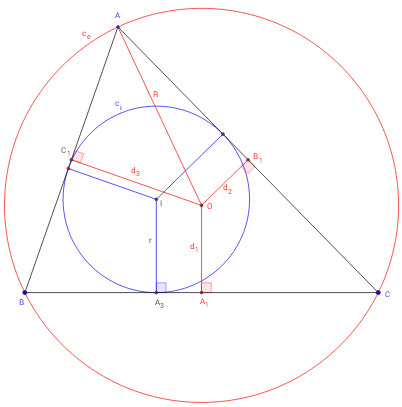
Théorème japonais de Carnot - angles aigus - figure GeoGebra - copyright Patrice Debart 2016

ABC est un triangle, C_eson cercle circonscrit de centre O et de rayon R et C_i son cercle inscrit de centre I et de rayon r.

Cas particulier où le triangle ABC a tous ses angles aigus.

Les projetés orthogonaux de O sur les côtés [BC], [AC] et [AB] sont A₁, B₁ et C₁.

Les distances du centre O aux côtés du triangle sont notées par d₁, d₂ et d₃.

La somme des distances du centre O aux côtés du triangle est donnée par

d₁ + d₂ + d₃ = R + r.

Figures interactives dans GeoGebraTube :
théorème japonais de Carnot - triangle avec des angles aigus

théorème japonais de Carnot - triangle avec un angle obtus

démontration du théorème japonais de Carnot

Voir : Théorème japonais de Carnot dans le triangle rectangle

Voir aussi

Théorème de la bissectrice :
Si I et J sont les pieds des bissectrices sur (BC),
alors IB/IC = JB/JC = c/b ;
et on les relations métriques :
bc = AI² + IB × IC et bc = JB × JC – AJ².

Théorèmes de la médiane

Théorème de Thalès

Théorème de Céva

Théorème de Ménélaüs

Triangle rectangle

Théorème de Pythagore : a² = b² + c² pour un triangle rectangle en A.

Relations métriques dans le triangle rectangle

Résoudre un triangle

Ces formules permettent de résoudre un triangle, c'est-à-dire d'en calculer les différents éléments à partir, d'en général, de trois données particulières.