Descartes et les Mathématiques

Triangles remarquables

Isocèle, équilatéral, médian, orthique, tangentiel…

Triangle

Définition

Un triangle est une figure plane, formée par trois points appelés sommets. Les côtés sont les segments qui joignent les sommets deux à deux.

Triangle plat

Un triangle plat est un triangle dégénéré dont les trois sommets sont alignés.

Par la suite, nous considérons des triangles non plats.

Triangle acutangle

en : acute-angled

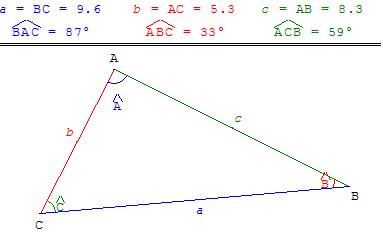
Triangle (non rectangle) dont les trois angles sont aigus.

Triangle obtusangle

Triangle ayant exactement un angle obtus.

Propriété : le centre du cercle circonscrit et l'orthocentre d'un triangle obtusangle sont situés à l'extérieur du triangle.

Triangle d'argent

Un triangle d'argent est un triangle isocèle ayant un angle 108°, les deux autres angles étant égaux à 36°.
Figure : voir triangle d'or

Triangle de Bevan

Pour un triangle donné, le triangle de Bevan formé par les bissectrices extérieures, a pour sommets les centres des cercles exinscrits au triangle.

Triangle bisocèle

Un triangle bisocèle est un triangle isocèle qui est partagé, par l'une de ses bissectrices, en deux triangles eux-mêmes isocèles.

Triangle équilatéral

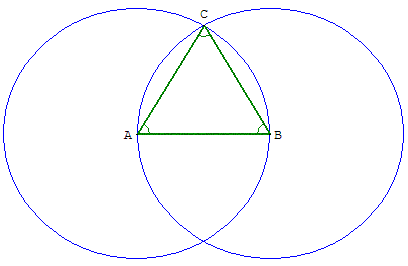
Un triangle équilatéral a ses trois côtés de même longueur,
les trois angles sont égaux et mesurent 60 degrés (soit radians).

Dans un triangle équilatéral, toutes les droites remarquables (médiane, hauteur, bissectrice, médiatrice) relatives à un même côté sont confondues.
Elles ont même longueur, égale à a, où a est la longueur du côté du triangle.
L'aire du triangle est égale à a².
Le centre de gravité du triangle équilatéral est confondu avec l'orthocentre et les centres des cercles inscrit et circonscrit.

Figure interactive dans GeoGebraTube : triangle équilatéral

Triangle de Feuerbach

Les quatre points de contact entre le cercle d'Euler et le cercle inscrit et les trois cercles exinscrits s'appellent les points de Feuerbach.
Les trois points de tangence des cercles exinscrits forment le triangle de Feuerbach du triangle.

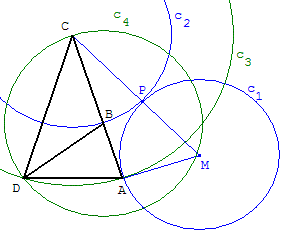
Triangle de Gergonne

Dans un triangle, le triangle de Gergonne a pour sommets les points de contact du cercle inscrit avec les côtés du triangle.

Triangle isocèle

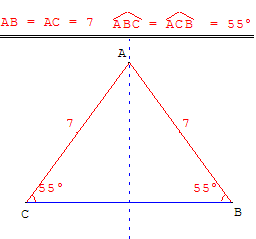
Un triangle isocèle a deux côtés de même longueur. Le troisième côté s'appelle la base.
Thalès a découvert que, dans un triangle isocèle, les angles à la base sont égaux.

Droites remarquables du triangle isocèle

La médiatrice de la base est axe de symétrie du triangle. Elle est aussi la médiane, la hauteur et la bissectrice relative à cette base.

L'orthocentre, le centre de gravité, le centre du cercle circonscrit et le centre du cercle inscrit sont tous situés sur cet axe de symétrie.

Figure interactive dans GeoGebraTube : triangle isocèle

Un triangle qui n'est pas isocèle est scalène : tous les côtés sont inégaux.

Un triangle équilatéral est un triangle isocèle particulier.

Triangle médian

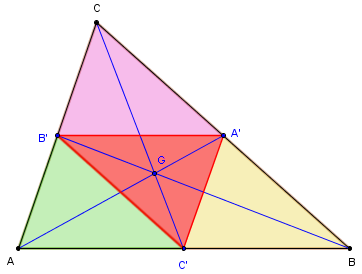
Le triangle qui joint les milieux des côtés d'un triangle est le triangle médian.

On l'appelle aussi triangle complémentaire ou triangle médial.

Figure interactive dans GeoGebraTube : triangle médian

Triangle de Nagel

Dans un triangle, le triangle de Nagel a pour sommets les points de contact des cercles exinscrits avec les côtés du triangle.

Triangle extérieur de Napoléon

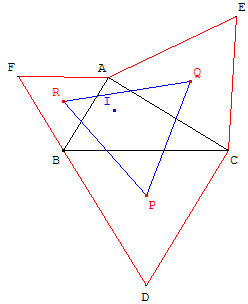
ABC est un triangle, dont tous les angles sont inférieurs à , bordé extérieurement par trois triangles équilatéraux BCD, ACE et ABF ayant pour centres de gravité respectifs P, Q et R.
Le triangle équilatéral PQR est le triangle extérieur de Napoléon.

Triangle d'or

Un triangle d'or est un triangle isocèle ayant un angle, au sommet, de 36° ; les deux autres angles, à la base, étant égaux à 72°.

Le triangles ACD et ABD sont d'or, BCD est d'argent.

Triangle orthique - Triangle de lumière

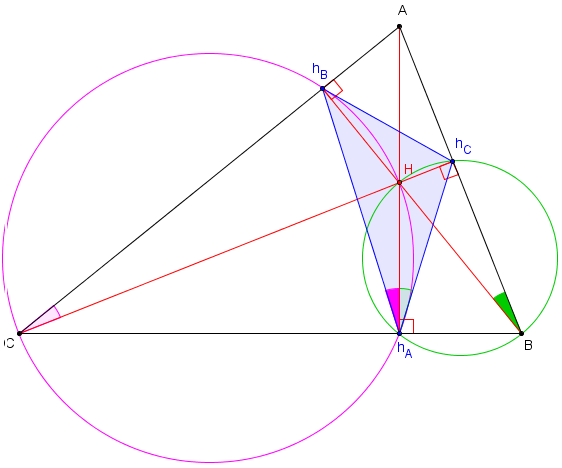
de : Höhenfußpunktdreieck

Le triangle qui joint les pieds des hauteurs d'un triangle ABC est le triangle orthique.

Dans un triangle ABC acutangle (non rectangle dont les trois angles sont aigus), les hauteurs (Ah_A), (Bh_B) et (Ch_C), concourantes en son orthocentre H, sont les bissectrices (h_AH), (h_BH) et (h_CH) du triangle orthique h_Ah_Bh_C.

Les côtés du triangle orthique sont perpendiculaires aux médiatrices du triangle ABC.

Le triangle inscrit dans un triangle qui a le plus petit périmètre est le triangle orthique.

Triangle de lumière : les côtés du triangle orthique se réfléchissent sur les bords du triangle ABC à la façon de rayons lumineux

Télécharger la figure GéoPlan t_orthiq3.g2w

WikiPédia : triangle orthique

Triangle pédal

en : cevian triangle

Le triangle pédal est parfois appelé triangle cévian.

Dans un triangle, une cévienne est une droite issue d'un sommet.

Soit ABC un triangle et un point I distinct des sommets. Les céviennes (AI), (BI) et (CI) coupent - en général - les côtés opposés du triangle en trois points A’, B’ et C’.

Le triangle A’B’C’, qui joint les pieds des trois céviennes (AA’), (BB’) et (CC’) concourantes en I, est le triangle pédal du point I par rapport au triangle ABC. Son cercle circonscrit est appelé cercle pédal de I par rapport au triangle ABC.

Le triangle pédal correspondant aux hauteurs est le triangle orthique, celui correspondant aux médianes est le triangle médian. Le cercle des neuf points est le cercle pédal de l'orthocentre et du centre de gravité.

Triangle rectangle

de : Rechtwinkliges Dreieck

Un des angles est droit, les deux autres angles sont aigus et complémentaires.

Le plus grand côté est l'hypoténuse : c'est le côté opposé à l'angle droit.
Les côtés adjacents à l'angle droit sont appelés cathètes

Thalès : un triangle rectangle s'inscrit dans un demi-cercle et réciproquement.
Cercle de Thalès du triangle rectangle : le demi-cercle dont le diamètre est l'hypoténuse.

Pythagore : la somme des carrés des longueurs des côtés de l'angle droit est égale au carré de la longueur de l'hypoténuse et réciproquement.

Triangles rectangles particuliers

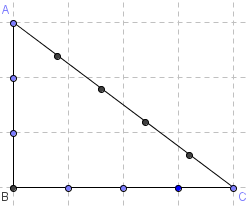
« Triangle égyptien » ou « triangle des arpenteurs »

Expressions clés :

Tracer un triangle rectangle avec une ficelle !
Tracer un angle droit avec une corde à 13 nœuds !
Tracer un angle droit sans équerre !
Tracer un rectangle sans équerre !
Équerre sans équerre.

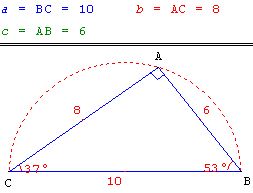
Le triangle rectangle de côtés (3, 4, 5), connu depuis l'Antiquité. Avec une « corde à 13 nœuds  » ou « corde égyptienne », les Anciens s'en servaient comme équerre, entre autres, pour reconstituer les champs après les crues du Nil.
Ce triangle a été utilisé de façon empirique pendant 2 000 ans, jusqu'à ce que Pythagore montre qu'il était rectangle.
Ce triangle est aussi appelé « triangle cosmique de Platon », « triangle sacré » ou encore « triangle d'Isis » nommé « triangle isiaque ».
C'est le plus petit « triangle de Pythagore » : triangles dont les longueurs des côtés sont des entiers.

Construction du triangle égyptien 

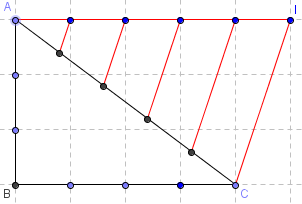
Le quadrillage de l'écran GeoGebra permet de répartir les points sur les petits côtés du triangle.

Pour le partage en cinq de l'hypoténuse, on peut utiliser une configuration de Thalès à partir du segment [AI] de longueur 5, en traçant les parallèles à (IC) et leurs quatre points d'intersections avec [AC].

Figures interactives dans GeoGebraTube : construction du triangle égyptien

« Demi-carré » ou « Triangle 45-45-90

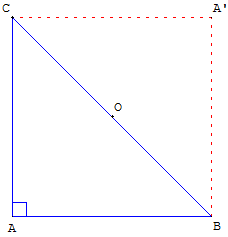
 »: c'est le triangle rectangle isocèle d'angles aigus de 45°,
de côtés (1, 1, ), c'est le format d'un certain nombre d'équerres.

La longueur de l'hypoténuse du triangle rectangle isocèle est égale à la longueur des petits côtés multipliée par racine de 2.

« Triangle de l'écolier » ou « Triangle 30-60-90 »

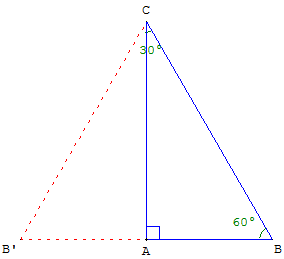
Demi-triangle équilatéral d'angles de mesures 30°, 60° et 90° ; format d'autres équerres utilisées à l'école.

Une autre construction avec un triangle équilatéral et un triangle isocèle, voir : exercices de géométrie au collège

Figure interactive dans GeoGebraTube : triangle de l'écolier

Triangle quelconque

Par nature, un triangle est quelconque.

Un triangle est dit « triangle quelconque » s'il n'est ni rectangle, ni isocèle (ce qui exclut également le cas équilatéral).

Un triangle peut posséder ou non des propriétés de triangles particuliers. Si on précise triangle quelconque, on peut penser que les côtés sont inégaux et qu'il n'y a pas d'angle droit.

Triangle scalène

Un triangle qui n'est pas isocèle est dit « scalène »

Un triangle scalène est un triangle :

• dont les trois côtés sont de longueurs inégales ;
• dont les trois angles sont de mesures différentes ;
• qui n'a pas d'axe de symétrie.

Un triangle scalène peut aussi être rectangle.

Un triangle qui n'est pas scalène est isocèle : deux ou trois côtés sont de longueurs égales.

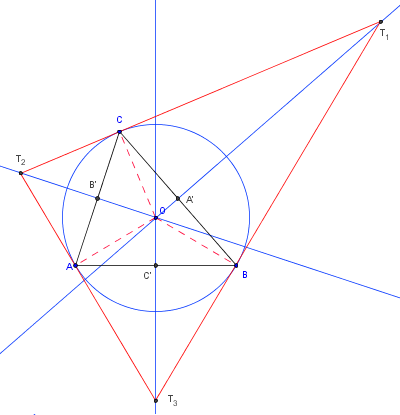
Triangle tangentiel

Pour un triangle ABC, de cercle circonscrit (c), les tangentes à (c) aux sommets A, B et C forment un triangle dit tangentiel du triangle ABC.

Triangle tangentiel et médiatrices

Les sommets T₁, T₂, T₃ sont situés sur les médiatrices (OA'), (OB'), (OC').
On a T₁B = T₁C ; T₂A = T₂C et T₃A = T₃B.

Triangle tangentiel et symédianes

Les symédianes joignent les sommets du triangle aux sommets du triangle tangentiel.
Elles sont concourantes et leur point de concours est le point de Lemoine.

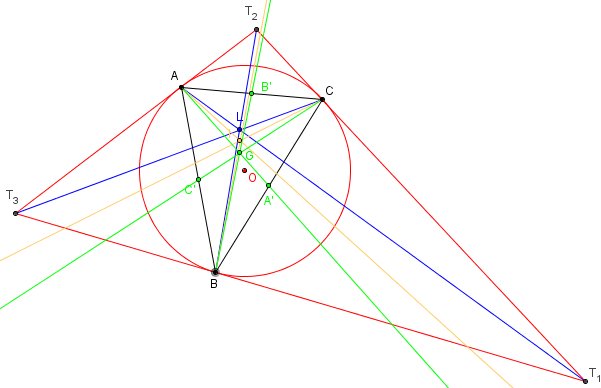
Les symédianes joignent les sommets du triangle aux sommets du triangle tangentiel.

Elles sont concourantes et leur point de concours est le point de Lemoine

Figures dans GeoGebraTube : triangle tangentiel

     symédianes et point de Lemoine

      point de Lemoine,

Figure exportée dans WikiPédia : triangle tangentiel

Voir aussi :

Polygone tangentiel : les côtés du polygone sont tangents à un même cercle, inscrit dans le polygone.
Quadrilatère tangentiel (ou circonscriptible) : Les quatre côtés sont tangents à un même cercle, inscrit dans le quadrilatère.

Trilatère

Un triangle est une figure trilatère (Euclide)

Table des matières

Dans d'autres pages du site

La géométrie du triangle

Retrouver un triangle à partir de trois droites remarquables

Construction de triangles en 5^e

Moteur de recherche

La fin du triangle : pour la recherche du mot « triangle », seulement trois résultats sur dix concernent la géométrie, et sans WikiPédia, le triangle mathématique disparaîtrait complètement !

Que penser de bing qui propose comme premier choix une boite d’intérim ?

Google friendly