Descartes et les Mathématiques

La géométrie du triangle II
Points caractéristiques

Points de Terquem, de Gergonne, de Nagel, de Bevan, de Brocard.

Sommaire

II. Points caractéristiques du triangle

1. Points de Terquem
    Céviennes
    Théorème de Céva
    Triangle pédal et cercle pédal

2. Droites antiparallèles, droites isogonales
    Quadrangle inscriptible

3. Symédianes
      Point de Lemoine
4. Points isogonaux
      Triangle podaire
5. Point de Gergonne

6. Point de Nagel

7. Point de Bevan

8. Points de Brocard

    Axe et cercle de Brocard

Points remarquables du triangle

1. Points de Terquem

Giovanni Céva (1648-1734)

Cévienne

Dans un triangle, une cévienne est une droite issue d'un sommet :
    – les hauteurs, médianes, bissectrices sont des céviennes,
    – les médiatrices ne sont pas des céviennes.

Théorème de Céva

Énoncé avec des mesures algébriques

Dans un triangle ABC, soit trois céviennes, distinctes des côtés.
La première passe par A et coupe le côté (BC) en A’,
la seconde passe par B et coupe le côté (AC) en B’ et
la troisième passe par C et coupe le côté (AB) en C’.

Les trois droites (AA’), (BB’) et (CC’) sont concourantes
(ou parallèles) si et seulement si :

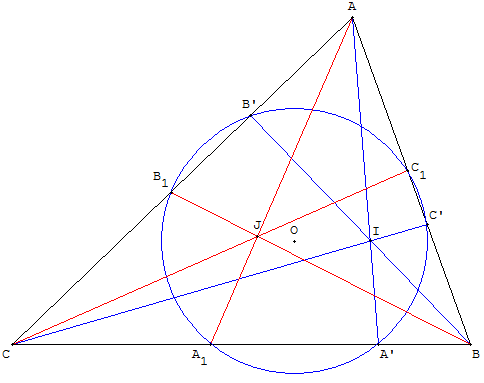
Trois céviennes concourantes en un point I,
coupent les côtés du triangle en A’, B’ et C’.
Le cercle pédal de I recoupe les côtés en A₁, B₁ et C₁.

Ces trois autres points A₁, B₁ et C₁ sont également les pieds de trois céviennes
concourantes en un point J , appelé conjugué cyclocévien de I.

Les points de Terquem sont les six points A’, B’, C’, A₁, B₁ et C₁.

WikiPédia : Théorème de Terquem

Énoncé avec des distances

À l'intérieur d'un triangle ABC, une première cévienne passe par A
et coupe le côté [BC] en A’, une seconde passe par B et coupe
le côté [AC] en B’ et une troisième passe par C et coupe le côté [AB] en C’.
Les trois céviennes (AA’), (BB’) et (CC’) sont concourantes
(ou parallèles) si et seulement si : A’B/A’C × B’C/B’A × C’A/C’B = 1.

Applications : le théorème de Céva permet de montrer
facilement que les médianes, les hauteurs
ou les bissectrices d'un triangle sont concourantes.
Il permet aussi de démontrer que les trois céviennes qui aboutissent
aux points de contact des côtés d'un triangle avec
le cercle inscrit sont concourantes au point de Gergonne.

On démontre de même que les trois céviennes qui aboutissent
aux points de contact des côtés d'un triangle avec
les cercles exinscrits sont concourantes au point de Nagel.

Triangle pédal

en : cevian triangle ; le triangle pédal est parfois appelé triangle cévian

Soit ABC un triangle et un point I distinct des sommets.
Les céviennes (AI), (BI) et (CI) coupent − en général −
les côtés opposés du triangle en trois points A’, B’ et C’.

Le triangle A’B’C’, qui joint les pieds des trois céviennes (AA’), (BB’) et (CC’)
concourantes en I, est le triangle pédal du point I par rapport au triangle ABC.
Son cercle circonscrit est appelé cercle pédal
(ou cercle de Terquem) de I par rapport au triangle ABC.

Le triangle pédal correspondant aux hauteurs est le triangle orthique,
celui correspondant aux médianes est le triangle médian.

Cercle pédal

Le cercle pédal d'un point est le cercle circonscrit
au triangle pédal correspondant.

Le cercle pédal, du centre du cercle inscrit, passe
par le point de Feuerbach du triangle.

Théorème de Terquem

Terquem Olry (1782-1862)

Soit ABC un triangle et trois céviennes
du triangle concourantes en un point I.
Le cercle pédal de I par rapport à ABC, passant par les pieds
de ces céviennes, détermine trois autres points sur les côtés du triangle.
Ces trois autres points sont également les pieds
de céviennes concourantes (en J sur la figure ci-dessus).
Ces six points sont appelés points de Terquem.

Cas particuliers

Lorsque les céviennes sont confondues deux à deux, le
cercle pédal est le cercle inscrit dans le triangle.
En effet, le cercle pédal touche le triangle en trois points
doubles qui sont les points de tangence.
Ces céviennes sont concourantes au point de Gergonne.

Lorsqu'un des triplés est formé par les médianes,
l'autre l'est par les hauteurs ou réciproquement ;
le cercle pédal de l'orthocentre et du centre de gravité
est alors le cercle des neuf points(cercle de Terquem).

L'orthocentre est le conjugué cyclocévien du centre de gravité.

Démonstration

D'après le théorème de Céva, si les trois droites (AA’),
(BB’) et (CC’) sont concourantes on a :

La puissance du point A par rapport au cercle circonscrit
à A’B’C’ est ,
d'où les rapports égaux : .
De même, la puissance de B permet d'écrire .
Enfin, la puissance de C permet d'écrire .
Le produit des rapports de gauche est égal à –1,
d'où produit des rapports de droite est aussi égal à –1,
d'où :

D'après la réciproque du théorème de Céva, les trois
droites (AA₁), (BB₁) et (CC₁) sont concourantes.

Céviennes isotomiques − Points réciproques

Avec les notations de l'article précédent, deux céviennes issues
d'un même sommet (A par exemple) sont dites isotomiques
lorsque leurs pieds A’ et A₁ sont symétriques par rapport au milieu du côté [BC].

Lorsque trois céviennes sont concourantes,
les trois céviennes isotomiques sont aussi concourantes.

Soit I le point de concours de trois céviennes (AA’), (BB’)
et (CC’), I non situé sur les côtés du triangle,
les trois céviennes isotomiques (AA₁), (BB₁) et (CC₁)
sont concourantes en J. Les points I et J sont dits réciproques l'un de l'autre.
Si le point I a pour coordonnées barycentriques (x ; y ; z), alors J,
le point réciproque de I a pour coordonnées barycentriques (1/x ; 1/y ; 1/z).

Les points de Gergonne et de Nagel sont deux points réciproques.

2.a. Droites antiparallèles, droites isogonales

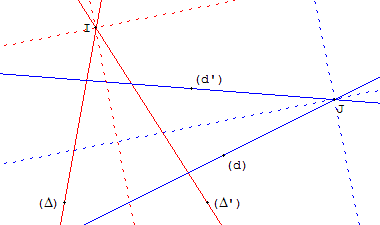
Droites antiparallèles

Deux couples de droites (d, d’) et (Δ, Δ’) sont antiparallèles
s'ils ont les mêmes directions de bissectrices.
Les angles de droites (d, Δ) et (Δ’, d’) sont égaux (modulo π).
On dit que (d’) est antiparallèle à (d) par rapport à (Δ, Δ’).

Figure exportée dans Wiki Pédia : droites antiparallèles

nl : Antiparallel

vièt : Điểm đẳng giác

Wiktionnaire : antiparallèle

2.b. Points cocycliques

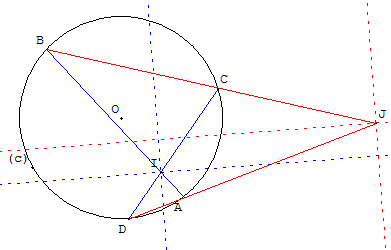
Quatre points A, B, C et D tels que trois d'entre eux ne sont pas alignés
sont cocycliques si et seulement si les droites (AB) et (DC) sont
antiparallèles par rapport aux droites (AD) et (BC).

2.c.Droites isogonales

Couple de droites isogonaux

en : isogonal conjugate

Deux couples de droites concourantes (d, d’)
et (Δ, Δ’) sont isogonaux s'ils sont antiparallèles.
Les angles de droites (d, Δ) et (Δ’, d’) sont égaux (modulo π).
On dit que (d’) est isogonale à (d) par rapport à (Δ, Δ’).

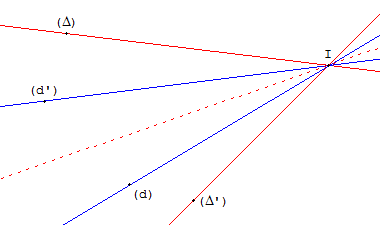
Si deux couples de droites (d, d’) et (Δ, Δ’) sont antiparallèles
et concourants, on dit qu'ils sont isogonaux.

Ils ont les mêmes bissectrices.
Les angles de droites (d, Δ) et (Δ’, d’) sont égaux (modulo π).

Application

Soit (d), (Δ), (Δ’) trois droites concourantes. La droite (d’) symétrique
de (d) par rapport à la bissectrice intérieure de (Δ) et (Δ’)
est isogonale à (d) par rapport à (Δ, Δ’).

Avec GéoPlan, il est facile de construire un prototype qui,
à partir deux droites (AB) et (AC) sécantes en A, d'un point M
et d'une droite (d), trace la droite (d’) passant par M,
antiparallèle à (d) par rapport à (AB) et (AC).

2.d.Quadrangle

Un quadrangle est la figure formée par quatre points A, B, C, D
tels que trois quelconques d'entre eux ne soient pas alignés :
ce sont les sommets du quadrangle.
Les six droites joignant ces points deux à deux sont les côtés du quadrangle.
Deux côtés qui n'ont pas de sommet en commun sont dits opposés.
Deux côtés opposés (non parallèles) ont un
point commun appelé point diagonal du quadrangle.
Un quadrangle complet (dont les côtés ne sont pas parallèles)
a quatre sommets, six côtés et trois points diagonaux.

Le quadrangle est à distinguer du quadrilatère complet
qui a six sommets, quatre côtés, trois diagonales et trois points diagonaux.

Dans un espace projectif, le dual d'un quadrangle
est un quadrilatère complet et réciproquement.

Quadrangle orthocentrique

Si H est l'orthocentre du triangle ABC,
A est l'orthocentre de BCH, B de ACH, C de ABH.

ABCH est un quadrangle orthocentrique.

2.e.Quadrangle inscriptible

Un quadrangle est inscriptible, si ses quatre sommets sont sur un même cercle.

Pour qu'un quadrangle soit inscriptible, il faut et il suffit que deux
couples decô tés opposés soient antiparallèles.
Le troisième couple est alors antiparallèle à chacun des deux autres.

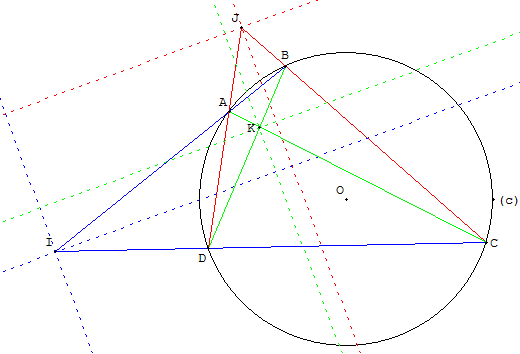
Soit ABCD un quadrangle dont les côtés opposés (AB) et (CD) se coupent en I.

ABCD est inscriptible si et seulement si :
IA × IB = IC × ID.

IA × IB est la puissance du point I par rapport au cercle circonscrit au quadrangle.

Les angles IÂD et ICB sont égaux. Les triangles IAD et ICB sont (inversement)
semblables (les angles inscrits DCB et DAB sont supplémentaires
dans la figure ci-dessus ou égaux dans la figure ci-dessous).

WikiPédia : Quadrangle

2.f. Droites antiparallèles aux côtés d'un triangle

Lorsqu'une droite est antiparallèle à un côté d'un triangle par rapport aux
deux autres on sous-entend assez souvent les deux derniers côtés.
On dira : « dans le triangle ABC la droite (d) est antiparallèle à (AB)»
à la place de «la droite (d) est antiparallèle à (AB) par rapport à (CA) et (CB) ».

Trois droites (d₁), (d₂) et (d₃) sont antiparallèles aux côtés d'un triangle ABC si :
la droite (d₁) est antiparallèle à (BC) par rapport à (AB) et (AC),
la droite (d₂) est antiparallèle à (AC) par rapport à (BA) et (BC),
la droite (d₃) est antiparallèle à (AB) par rapport à (CA) et (CB).

2.g. Points sur deux droites isogonales

Soit (Δ) et (Δ’) deux droites concourantes en A,
M et N deux points sur deux droites (d) et (d’) concourantes en A.

M₁ et N₁ sont les projections orthogonales de M et N sur (Δ), M₂ et N₂ sur (Δ’).

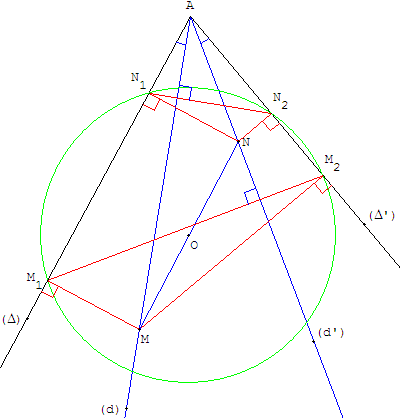
Théorème

Les deux couples de droites (Δ, Δ’) et (d, d’) sont isogonaux si
et seulement si les points M₁N₁M₂N₂ sont cocycliques.

Indications

Le centre O du cercle est le milieu de [MN].

(N₁N₂) est orthogonale à (d), (M₁M₂) est orthogonale à (d’).

3. Symédianes et point de Lemoine

Définition

La symédiane issue du sommet A d'un triangle ABC est la droite (d) telle
que l'angle, formé par cette droite (d) et la médiane (AA’)
issue de A, ait pour bissectrice la bissectrice de BÂC.
C'est l'isogonale de la médiane par rapport aux côtés de l'angle Â.

Point de Lemoine (1873)

Lemoine Émile, mathématicien français
spécialiste de la géométrie du triangle, 1840-1912

Les trois symédianes d'un triangle sont concourantes.

Leur point de concours est le point de Lemoine, ou point de Grebe
ou encore point symédian du triangle (point X(6) dans ETC).

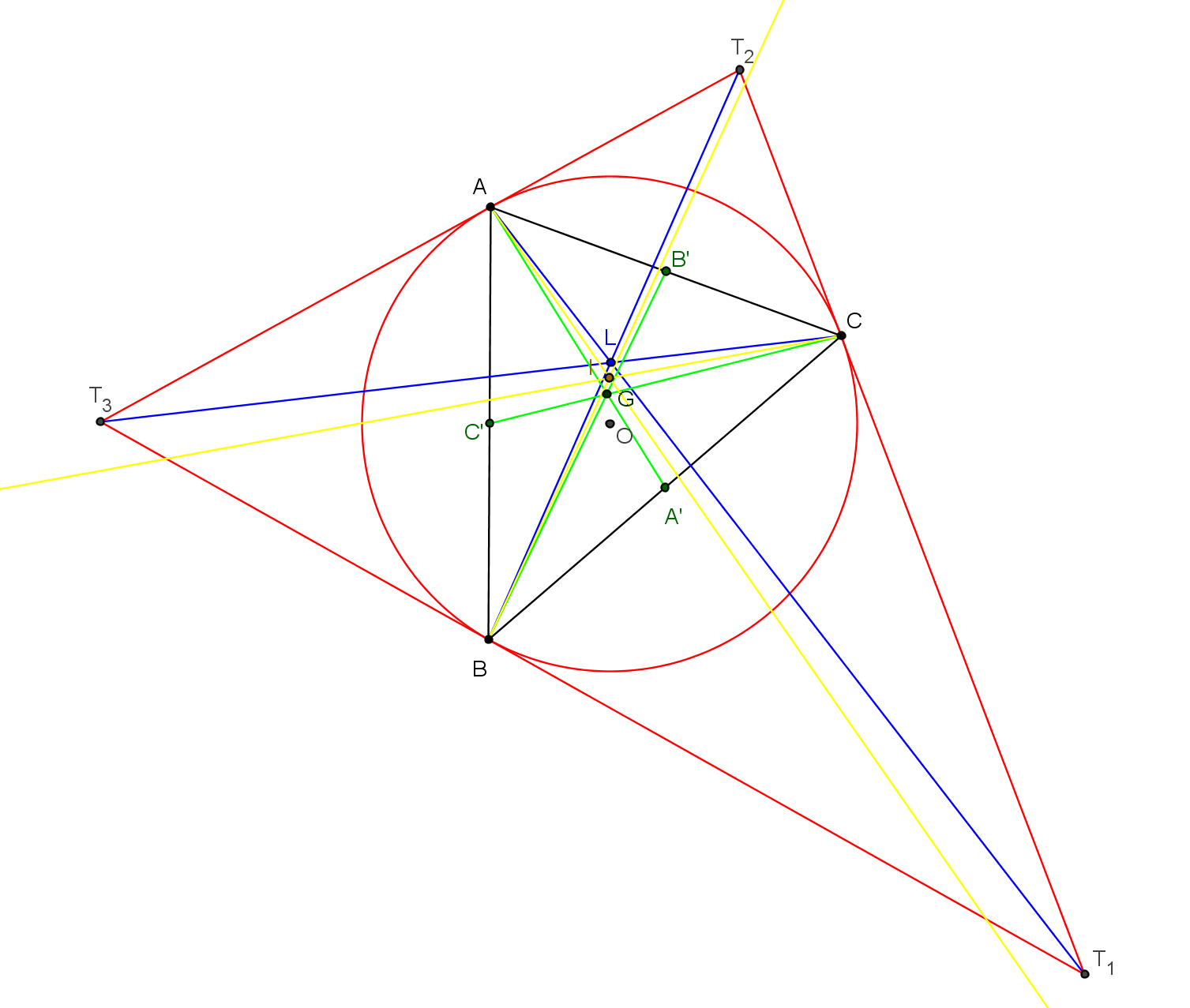
Les symédianes joignent les sommets du triangle aux sommets du
triangle tangentiel formé par les tangentes à son cercle circonscrit (Γ).

Les distances de ce point aux trois côtés du triangle
sont proportionnelles aux côtés.
Le point de Lemoine du triangle ABC, de côtés a = BC, b = CA
et c = AB est le barycentre du système pondéré (A, a²) ; (B, b²) ; (C, c²).
Le point de Lemoine est le point dont la somme des
carrés des distances aux côtés du triangle est minimale.

Le point de Lemoine L est le point de Gergonne du triangle tangentiel
(point X(7)).

Figures dans GeoGebraTube : point de Lemoine,

      triangle tangentiel

Figure exportée dans WikiPédia: symédiane

Voir : construction avec trois carrés autour d'un triangle,

cercles de Tücker

 Glossaire publimath

Propriétés du point de Lemoine

Les distances de ce point aux trois côtés du triangle
sont proportionnelles à ses côtés.
Le point de Lemoine du triangle ABC,
de côtés a = BC, b = AC et c = AB est le barycentre
du système pondéré (A, a²) ; (B, b²) ; (C, c²).
C'est le point L dont la somme des carrés des
distances aux côtés du triangle est minimale.

Droite de Lemoine

Intersection des côtés du triangle avec ceux du triangle tangentiel.

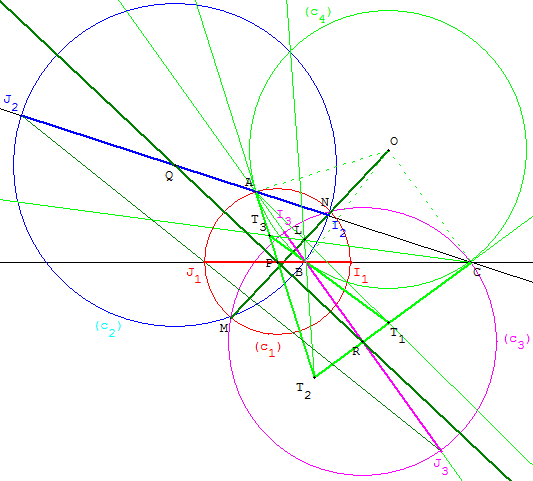
La tangente en A au cercle circonscrit coupe le côté (BC) en P,
la tangente en B coupe (AC) en Q, la tangente en C coupe (AB) en R.

Ces trois points sont alignés sur la droite de Lemoine du triangle ABC,
qui est la polaire du point de Lemoine par rapport à
ce cercle circonscrit au triangle.

Les points P, Q, R sont les centres des cercles d'Apollonius du triangle ABC.

L'axe de Brocard du triangle est la droite (OL) passant par
le centre du cercle circonscrit et par le point de Lemoine.
Il contient les centres isodynamiques M et N,
points d'intersection des cercles d'Apollonius ;
l'axe de Brocard est perpendiculaire à la droite de Lemoine (PQ).

Voir : cercles de Tücker,  

cercles de Lemoine,  

figure de Vecten

Milieu d'une antiparallèle

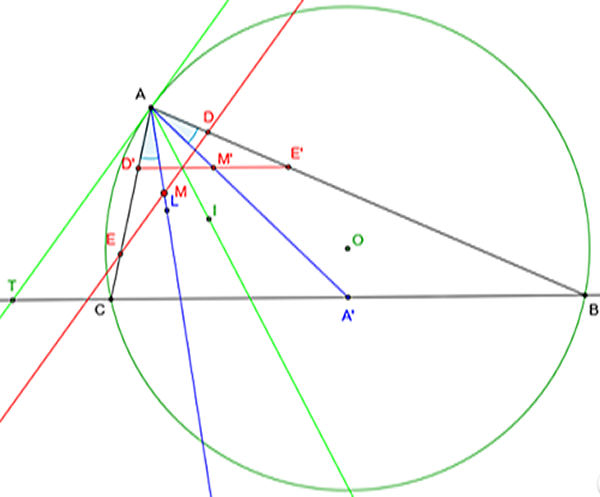
La symédiane coupe une antiparallèle au côté opposé en son milieu.

En effet, dans le triangle ABC, soit (DE) une antiparallèle à (BC)
qui coupe la symédiane de sommet A en M. L'antiparallèle (DE)
est parallèle à la tangente en A au cercle circonscrit de ABC.

Par la symétrie d'axe la bissectrice (AI) de BÂC, les points D, M, E
ont pour images D’, M’, E’. (D’E’) est parallèle à (BC). M’,
situé sur la médiane [AA’], est le milieu de [D’E’].
Par symétrie réciproque, M est le milieu de [DE].

Figure dans GeoGebraTube :
symédiane et milieu d'une antiparallèle au côté d'un triangle

Autre démonstration

Dans le triangle ABC, soit M le milieu de (DE) une antiparallèle à (BC).
Montrons que (AM) est la symédiane passant par A :

En effet, la droite (AM) est conjuguée harmonique de la tangente en A à (Γ)
par rapport à (AB, AC). La droite (AM) est donc la polaire, par rapport à (Γ)
du point T, intersection de (BC) avec la tangente en A à (Γ).
Par réciprocité polaire, la droite (AM) contient le pôle T₁ de (BC).
(AM) est la symédiane issue de A.

4. Points isogonaux

Triangle podaire

en : pedal triangle ; à ne pas confondre avec le triangle pédal.

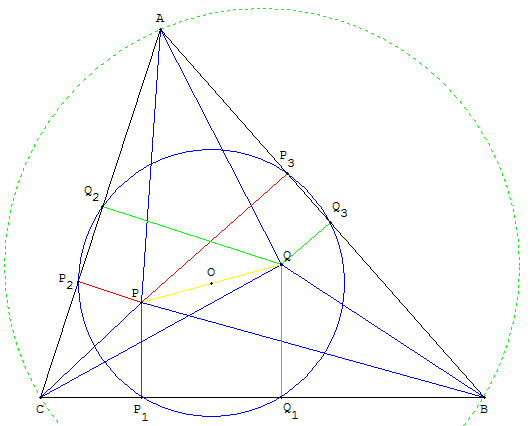
Soit P un point distinct des sommets du triangle ABC et n'appartenant pas au
cercle circonscrit, P₁, P₂, P₃ sont les projections orthogonales de P
sur les côtés du triangle.

P₁P₂P₃ est le triangle podaire du point P relativement au triangle ABC.

Le cercle circonscrit au triangle P₁P₂P₃ est le cercle podaire
du point P par rapport au triangle ABC.

Point conjugué isogonal

de : Isogonal konjugierte Punkte

Dans un triangle, deux points sont conjugués isogonaux
s'ils sont situés aux intersections de deux couples de
droites isogonales, issues de deux sommets.

Ils sont alors situés sur un couple de droites isogonales,
issues du troisième sommet.

Si un point P a pour coordonnées barycentriques (x ; y ; z),
alors Q, le conjugué isogonal de P a pour coordonnées
barycentriques (a²/x ; b²/y ; c²/z).

Les triangles podaires de deux points isogonaux P et Q sont
inscrits dans un même cercle de centre O, le milieu de [PQ].
Cette propriété permet la construction du
point isogonal par l'intermédiaire du cercle podaire.

WikiPédia : Conjugué isogonal

Wiktionnaire : isogonale

Dans un triangle, deux points sont conjugués isogonaux
s'ils situés aux intersections de deux couples de droites
isogonales, issues de deux sommets.
Ils sont alors situés sur un couple de droites isogonales,
issues du troisième sommet.

Exemples :

Les centres des cercles inscrit et exinscrits
coïncident avec leurs conjugués isogonaux
(ces cercles sont les cercles podaires de leur centre).

Le centre du cercle circonscrit est le conjugué isogonal de l'orthocentre
(une conséquence du théorème de Nagel, d'où des propriétés
intéressantes de la droite d'Euler et du cercle de Feuerbach).

Le point de Lemoine est le conjugué isogonal du centre de gravité.

Les deux points de Brocard sont des conjugués isogonaux.

5.a. Point de Gergonne

Gergonne Joseph (mathématicien français 1771-1859)

Le point de Gergonne est le point de concours des trois céviennes
qui aboutissent aux points de contact des côtés d'un
triangle avec le cercle inscrit (point X(7) dans ETC).

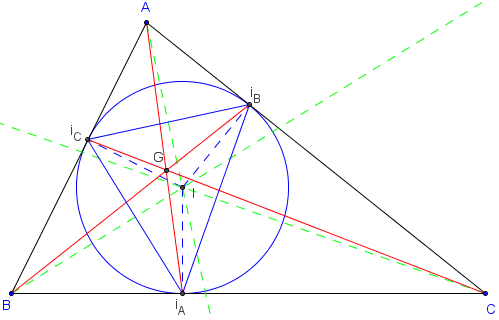
Les six céviennes sont alors confondues deux à deux,
les points de Terquem sont trois points doubles i_A, i_B et i_C points de contact
du cercle pédal qui est le cercle inscrit dans le triangle ABC.
Ce cercle est tangent intérieurement aux trois côtés du triangle en i_A, i_B et i_C.
Ces céviennes (Ai_A), (Bi_B) et (Ci_C) sont concourantes en un même point G,
point de Gergonne du triangle ABC.

Le point G est le barycentre de
(A, tan) ; (B, tan) ; (C, tan).

Le point G est son propre conjugué cyclocévien.

Le triangle i_Ai_Bi_C s'appelle le triangle de Gergonne
ou triangle de contact du triangle ABC.

Les trois bissectrices (intérieures) du triangle ABC sont concourantes en I,
centre du cercle inscrit dans le triangle.

Le triangle i_Ai_Bi_C s'appelle le triangle de Gergonne
ou triangle de contact du triangle ABC.

en : contact triangle

Le point de Gergonne G est le point de Lemoine
du triangle de Gergonne i_Ai_Bi_C.

Figure dans GeoGebraTube : point de Gergonne

Preuve

Pour chacun des sommets, les deux tangentes déterminent deux
segments, du sommet aux points de contact, de longueurs égales :
Ai_B = Ai_C, ainsi que Bi_A = Bi_C et Ci_A = Ci_B.

On a : Ai_C/Bi_C × Bi_A/Ci_A × Ci_B/Ai_B = 1.
La relation de Céva est donc vérifiée.

Les céviennes (Ai_A), (Bi_B) et (Ci_C) sont bien concourantes en G,
nommé point de Gergonne.

5.b. Droite de Gergonne

Le triangle de référence ABC et le triangle de Gergonne
i_Ai_Bi_C sont en perspective de pôle G, le point de Gergonne.

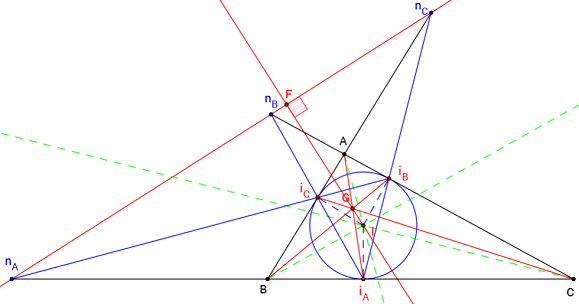
La forme forte du théorème de Desargues montre que les points de Nobbs,
points de concours n_A, n_B et n_C des côtés du triangle ABC
et du triangle de Gergonne, sont alignés sur la droite de la
perspective (perspectrix ou axe d'homologie) nommée droite de Gergonne.

La droite de Soddy (IG) (I centre du cercle inscrit) est perpendiculaire
en F (Point de Fletcher X(1323)) à la droite de Gergonne.

Figure dans GeoGebraTube : droite de Gergonne

6. Point de Nagel

Le point de Nagel est le point de concours des trois céviennes qui
aboutissent aux points de contact des côtés d'un triangle avec
les cercles exinscrits (Point X(8) dans ETC).

Cercles exinscrits

Deux bissectrices extérieures, associées à deux sommets,
et la bissectrice intérieure, associée au troisième sommet,
sont concourantes.

Leur point d'intersection est à égale
distance des trois côtés du triangle. Il permet de tracer
un cercle exinscrit, tangent aux trois côtés du triangle.

Soit (c₁), (c₂) et (c₃) les trois cercles exinscrits
au triangle ABC. Notons T_A, T_B et T_C leurs centres.

Notons u_A le point de contact de (c₁) avec [BC], u_B le point de
contact de (c₂) avec [AC] et u_C le point de contact de (c₃) avec [AB].

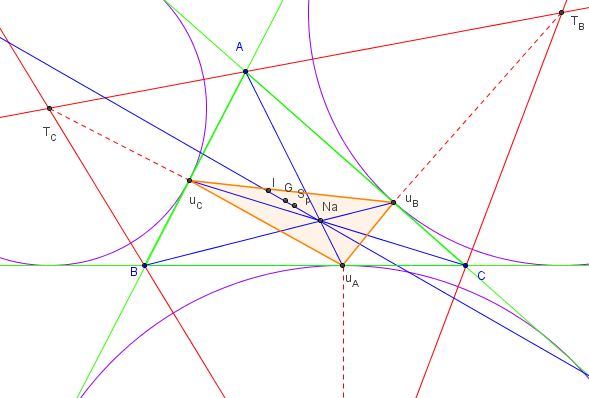
Le calcul des distances des sommets aux points de contact donne :
Bu_A = p – c ; Cu_A = p – b ; Au_B = p – c ;
Cu_B = p – a ; Au_C = p – b ; Bu_C = p – a.

On a : Au_C/Bu_C × Bu_A/Cu_A× Cu_B/Au_B = 1.
La relation de Céva est vérifiée :
les droites (Au_A), (Bu_B) et (Cu_C) sont concourantes ;
leur point d'intersection s'appelle le point de Nagel du triangle.

Le triangle u_Au_Bu_C qui a pour sommets les points de contact
des trois cercles exinscrits
avec les côtés du triangle ABC, est le triangle de Nagel du triangle ABC.

Point de concours

Les céviennes (Au_A), (Bu_B) et (Cu_C) sont concourantes au point de Nagel N_a.

Figure dans GeoGebraTube : point de Nagel

Droite de Nagel

La droite de Nagel passe par le centre de gravité G,
le centre du cercle inscrit I et le point de Nagel N_a.

Le point G est au tiers de IN_a, à partir de I.

Le centre de Spieker (X(10)) est aussi sur cette droite.
c'est le centre du cercle inscit dans le triangle médian.

Cercle inscrit dans le triangle médian

Le point de Nagel est le barycentre de :

(A, – a + b + c) ; (B, a – b + c) ; (C, a + b – c).

Points de contact des cercles inscrit
et exinscrit avec un côté du triangle

On a vu, dans la page cercles inscrit et exinscrit, que le point de contact R
du cercle inscrit avec [AB] vérifie AR = p – a. Comme BC’ = p – a,
les points R et C’ sont symétriques par rapport au milieu C₁ de [AB].

Cercle inscrit dans le triangle médian

Le cercle inscrit dans le triangle médian du triangle ABC a son centre J
situé sur la droite de Nagel. J est le milieu de [NI].

Par homothétie de centre N et de rapport ,
le cercle inscrit dans le triangle ABC
a pour image le cercle inscrit dans le triangle médian du triangle ABC.

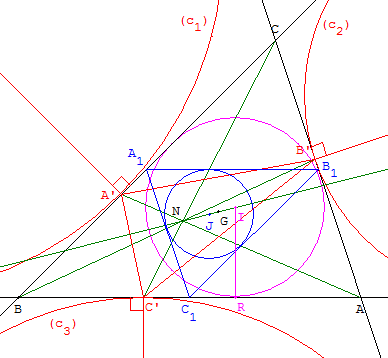
7. Point de Bevan

Soit A’B’C’ les points de contact des côtés d'un triangle
ABC avec les cercles exinscrits de centres I₁, I₂, I₃.

Les droites (I₁A’), (I₂B’) et (I₃C’) sont concourantes :
leur point d'intersection J s'appelle le point de Bevan
du triangle ABC (point X(40) dans ETC).

Le triangle I₁I₂I₃, formé par les bissectrices extérieures, de sommets
les centres des trois cercles exinscrits, s'appelle le triangle de Bevan
du triangle ABC.

en : excentral triangle or extriangle

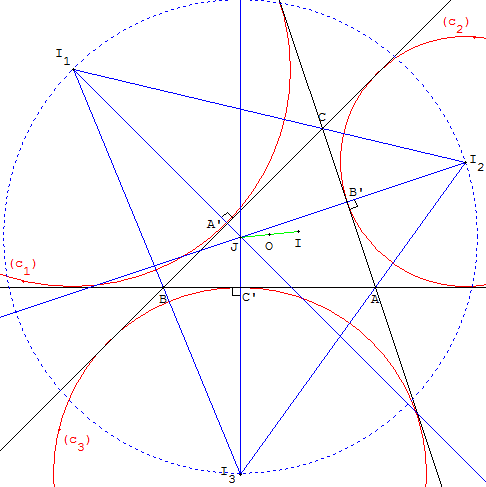
Propriétés du point de Bevan

Le point de Bevan J est le symétrique du centre I du cercle
inscrit par rapport au centre O du cercle circonscrit à ABC.

Le point de Bevan est le centre du cercle circonscrit
au triangle de Bevan I₁I₂I₃.
Le rayon du cercle circonscrit au triangle de Bevan est
le double de celui du cercle circonscrit au triangle ABC.

Figure interactive dans GeoGebraTube : point de Bevan

Hauteurs du triangle de Bevan

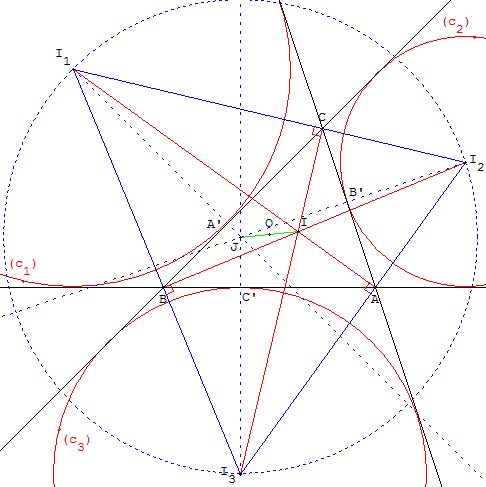
Le centre I du cercle inscrit est l'orthocentre du triangle de Bevan.

Le triangle ABC est le triangle orthique du triangle de Bevan.

Le point de Bevan est le centre du cercle inscrit dans le triangle J₁J₂J₃
construit avec les tangentes communes aux cercles exinscrits.

en : extangents triangle.

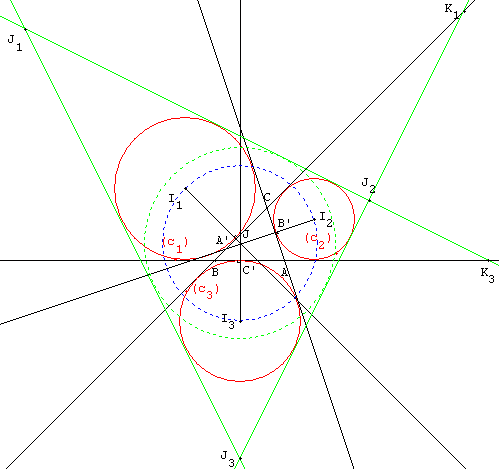
Ces tangentes sont trois droites, symétriques des côtés
par rapport aux lignes des centres :
    – la droite (J₁J₂), symétrique de (AB) par rapport à (I₁I₂),
rencontre (AB) en K₃ ;
    – (J₂J₃), symétrique de (BC) par rapport à (I₂I₃), passant par K₁
    – et (J₁J₃), symétrique de (AC) par rapport à (I₁I₃), passant par K₂.

Triangles de Bevan et Gergonne

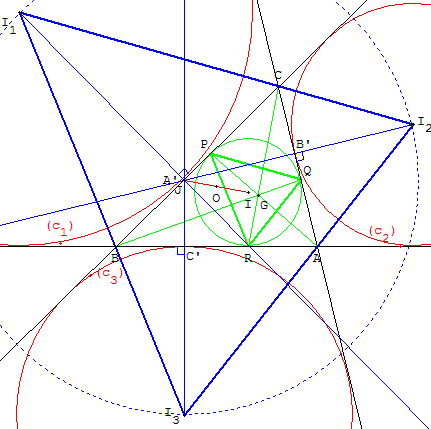
P, Q et R sont les points de contact du cercle inscrit
dans ABC. G est le point de Gergonne de ABC.

Le triangle de Bevan I₁I₂I₃ et le triangle de Gergonne PQR
sont homothétiques.

Triangle médian du triangle de Bevan

Les milieux A₁, B₁, C₁des côtés du triangle I₁I₂I₃ de
Bevan sont situés sur le cercle circonscrit à ABC.

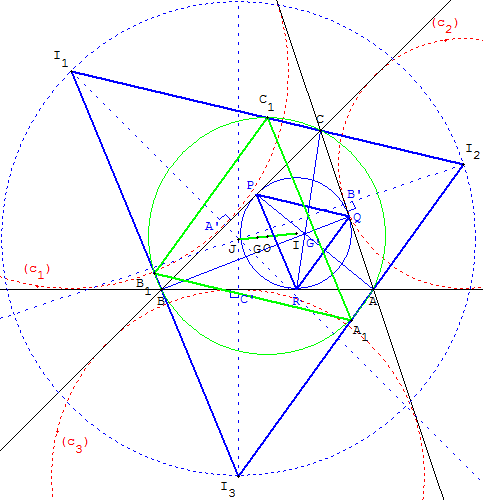
Le triangle médian A₁B₁C₁ est homothétique au triangle
de Bevan I₁I₂I₃ et au triangle de Gergonne PQR.

J est le point de Bevan. O est le centre du cercle circonscrit à ABC.
G est le centre de gravité du triangle de Bevan I₁I₂I₃,
G’ est le point de Gergonne de ABC.

Le rayon du cercle circonscrit au triangle I₁I₂I₃ est le double
de celui du cercle circonscrit au triangle ABC.

Voir aussi : problèmes d'antan

Triangle de Bevan d'un triangle rectangle

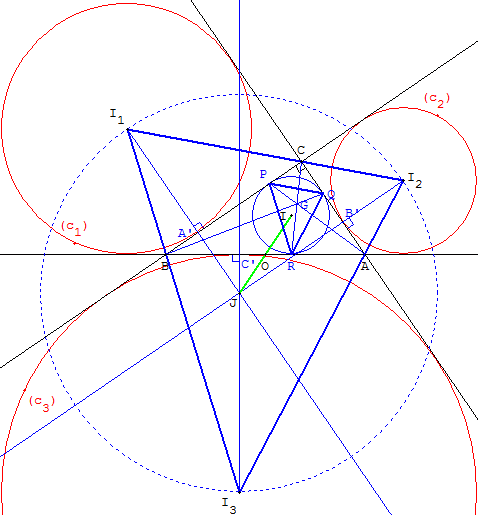
Pour un triangle rectangle, le point de Bevan est le symétrique
du centre du cercle inscrit par rapport au milieu de l'hypoténuse.

I est le centre du cercle inscrit dans ABC,
G est le point de Gergonne de ABC.

8. Points de Brocard

Ces points tirent leur nom du mathématicien Henri Brocard.
Ils ont été trouvés, en réalité par Jacobi et, en 1816, par Crelle.

Le premier point de Brocard d'un triangle ABC est le point Ω,
tel que les angles ΩAB, ΩBC et ΩCA orientés positivement soient égaux.

Le second point de Brocard du triangle est le point Ω’, tel que
les angles Ω’BA, Ω’CB et Ω’AC orientés positivement soient égaux.

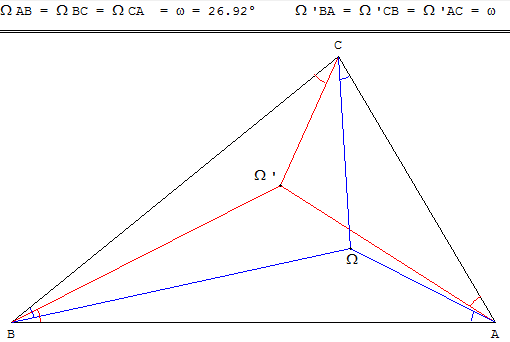
Les segments joignant les points Ω et Ω’ aux sommets
du triangle constituent des isogonales du triangle ABC.
Les angles ΩAB, ΩBC,ΩCA ; Ω’BA, Ω’CB et Ω’AC quelles définissent
avec les côtés du triangle sont tous égaux à l'angle de Brocard du triangle, noté ω.

Cet angle ω peut être calculé au moyen de sa cotangente par la formule :
cotan ω = cotan + cotan + cotan = où S désigne l'aire du triangle,
tan ω = .

Enfin, on appelle droite de Brocard l'une quelconque des droites
joignant un sommet du triangle à l'un des points de Brocard.

Le premier point de Brocard est le barycentre
de (A, ) ; (B, ) ; (B, )
et le second point de Brocard est le barycentre
de (A, ) ; (B,) ; (B, ).

Les points de Brocard sont " bicentric " ; ce ne sont pas des " centres "
du triangle et ils ne sont pas associés à des nombres de Kimberling.

Premier point de Brocard - construction géométrique

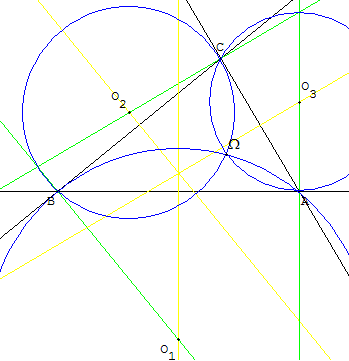
Étant donné un triangle ABC,
tracer le cercle passant par A et B et tangent à (BC),
le cercle passant par B et C et tangent à (CA)
et le cercle passant par C et A et tangent à (AB).

Ces trois cercles sont sécants en Ω, premier point de Brocard du triangle ABC.

Figure exportée dans WikiPédia : Premier point de Brocard

Deuxième point de Brocard

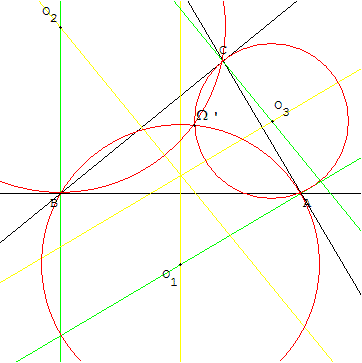
De même, tracer le cercle passant par A et B et tangent à (AC),
le cercle passant par B et C et tangent à (BA)
et le cercle passant par C et A et tangent à (CB).

Ces trois cercles sont sécants en Ω’, second point de Brocard du triangle.

Figure exportée dans WikiPédia : Deuxième point de Brocard

Axe et cercle de Brocard

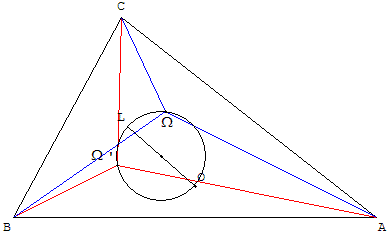
L'axe de Brocard du triangle est la droite passant par le centre
du cercle circonscrit et par le point de Lemoine.

Les points de Brocard, le point de Lemoine L
et le centre O du cercle circonscrit
sont sur un même cercle, cercle de Brocard du triangle.
[OL] est un diamètre de ce cercle, dit diamètre de Brocard.

Les points de Brocard sont symétriques
par rapport à l'axe de Brocard (OL).

Les deux points de Brocard sont conjugués isogonaux l'un de l'autre.

La médiane, issue d'un sommet du triangle ;
la symédiane, issue d'un second sommet ;
et une des droites de Brocard, issue d'un
troisième sommet, sont concourantes.

Remarque : ne pas confondre les droites de Brocard
(AΩ), (AΩ’), (BΩ’)… et l'axe de Brocard (OL).

Théorème d'Alasia

Cristoforo Alasia mathématicien italien 1869-1918

Théorème d'Alasia :
Le triangle ABC est isocèle en C si, et seulement
si, la droite (ΩΩ’) est parallèle à la base (AB).

Table des matières

Dans d'autres pages du site

Géométrie du triangle

I.  Droites remarquables

III. Droite et cercle d'Euler

     Cercles - Feuerbach

IV. Lieux géométriques

 V. Relations métriques

Triangle rectangle

Triangle équilatéral

Théorème de la médiane

Exercices

Construction de triangles en cinquième,

      au lycée

Le triangle au collège

Le triangle en seconde

Recherche de triangles connaissant des droites remarquables,
les pieds de droites remarquables

Droites de Simson et de Steiner (ménéliennes)

Google friendly ; sur ordinateur, version desktop