Descartes et les Mathématiques
Polaire par rapport à deux droites, à un cercle
Polaire d'un point par rapport à une paire de droites, par rapport à un cercle.
Sommaire
1. Polaire d'un point par rapport à deux droites
Transformation par polaires réciproques
5. Transformation des médianes d'un triangle
6. Transformation des hauteurs d'un triangle
Hors programme du lycée :
page destinée aux étudiants du CAPES et aux professeurs du secondaire
La notion projective de « polaire d'un point par rapport à une paire de droites » est complétée par la « polaire d'un point par rapport à un cercle ». Elle peut se généraliser à celle de « polaire d'un point par rapport à une conique ».
Dualité : si un point M a pour polaire une droite (d), alors tout point de (d) a une polaire qui passe par M. Toute droite qui passe par M à son pôle sur (d).
Réciprocité polaire : un point M est sur une droite (d) si et seulement si la polaire de M contient le pôle de (d).
Transformation par polaires réciproques : c'est la correspondance entre point et droite définie par l'association pôle et polaire.
Cette transformation renverse les incidences : trois pôles alignés correspondent à trois polaires concourantes et réciproquement.
Quatre points alignés en division harmonique correspondent à un faisceau harmonique de quatre droites.
1. Polaire par rapport à deux droites
Définition : étant donné deux droites (d) et (d’) et deux points M et M1 distincts, non
situés sur ces droites, la droite (MM1’) rencontre respectivement (d) et (d’) en P et P’ distincts.
On dit que M et M1 sont conjugués harmoniques par rapport à (d) et (d’) si [M, M1, P, P’] forme une division harmonique.
Définition : étant donné deux droites (d) et (d’) distinctes et concourantes en un point I du plan affine et un point M non situé sur ces droites, l'ensemble des conjugués harmoniques du point M par rapport à (d) et (d’) est une droite, passant par I. On appelle cette droite la polaire de M par rapport à (d) et (d’).
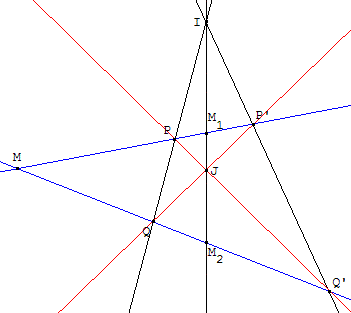
Construction de la polaire (à la règle seule) : étant donné deux droites (d) et (d’), concourantes en I, et un point M non situé sur ces droites, placer deux points P et Q, distincts et différents de I,
sur (d) et tracer les deux droites (MP)
et (MQ). Ces droites coupent d’ respectivement en P’ et Q’. On obtient le quadrilatère complet MPP’Q’QI. Ses diagonales Δ = (PQ’) et Δ’ = (P’Q) se coupent en J. La droite (IJ) est la polaire de M par rapport à (d) et (d’).
Démonstration : si M1 est le conjugué de M par rapport à P et P’ et M2 le conjugué de M par rapport à Q et Q’, la polaire de M par rapport à (d) et (d’) est la droite (M1M2) ; les points I, M1 et M2 sont alignés. De même, la polaire de M par rapport à Δ et Δ’ est la droite (M1M2) ; les points J, M1 et M2 sont alignés et la polaire de M par rapport à (d) et (d’) est la droite (IJ).
Réciprocité polaire : si la polaire de M passe par J, alors la polaire de J passe par M.
Télécharger la figure GéoPlan polaire.g2w
Applications
– Constructions par polaires réciproques :
droites concourantes : intersection inaccessible
droites parallèles : construction à la règle seule
– Construction d'un conjugué harmonique en utilisant la figure ci-dessus
Étant donné trois points distincts alignés M, P et P’, pour trouver le conjugué harmonique M1 de M par rapport à P et P’ :
– placer un point I à l'extérieur de (MP),
– tracer les droites (IP) et (IP’),
– placer un point Q sur la droite (IP) ; La droite (MQ) coupe (IP’) en Q’.
– les diagonales (PQ’) et (P’Q) du quadrilatère complet ainsi formé se coupent en J,
– la droite (IJ) coupe (MP) en M1. [P, P’, M, M1] est la division harmonique cherchée.
Images exportées dans WikiPédia : division harmonique
2. Faisceau et division harmonique
2.a. Faisceau harmonique - Définition
[A, B, C, D] étant une division harmonique située sur une droite (d) et O un point à l'extérieur de (d), les droites (OA), (OB), (OC) et (OD) forment un faisceau harmonique.
Comme [A, B, C, D] = -1, on écrit par convention [OA, OB, OC, OD] = −1.
Un faisceau harmonique découpe sur toute droite, non parallèle à un des rayons, une division harmonique.
Une parallèle à un des rayons du faisceau est divisée par les trois autres en deux segments égaux (condition nécessaire et suffisante).
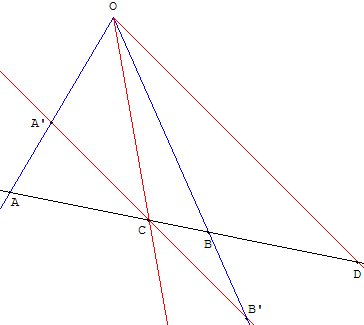
Explication
Soit la droite (A’B’) parallèle au rayon (OD) passant par C.
On a CA’ = CB’.
Pour le démontrer, voir les triangles semblables ACA’ et ADO d'une part, BCB’ et BDO d'autre part,
et utiliser la relation : 
= − 
.
Télécharger la figure GéoPlan faisceau_harmonique.g2w
2.b. Construire le quatrième point d'une division harmonique
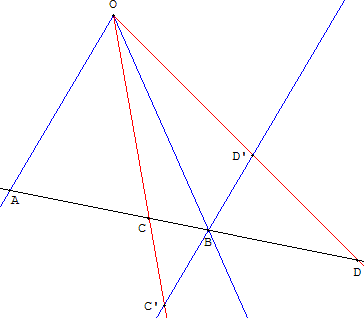
Application
Les trois points alignés A, B, C étant donnés, construire le quatrième point D tel que :
[A, B, C, D] = 
= −1.
Soit O un point non aligné avec les points précédents ; la parallèle à (OA) passant par B coupe (OC) en un point C’.
Soit D’ le symétrique de C’ par rapport à B, alors (OD’) coupe (AB) en D qui est le point cherché.
Figure interactive dans GeoGebra Tube : Division harmonique - Construction
2.c. Bissectrices intérieure et extérieure d'un angle
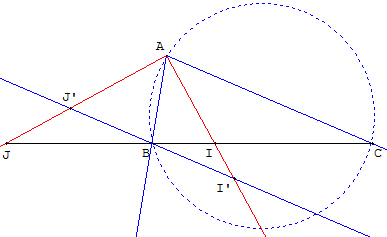
Dans un triangle ABC, les bissectrices intérieure (AI) et extérieure (AJ) coupent le côté (BC) en I et J. On dit que les points I et J divisent harmoniquement le segment [BC].
[B, C, I, J] est une division harmonique est équivalent au fait que les droites (AB, AC, AI, AJ) forment un faisceau harmonique.
Démonstration
En construisant une parallèle au côté (AC) passant par B, qui coupe les deux bissectrices en deux points I’ et J’, on montre, en étudiant les angles, que les triangles ABI’ et ABJ’ sont isocèles en B. Le point B est le milieu de [I’J’]. Une parallèle à un des rayons du faisceau est divisée par les trois autres en deux segments égaux, donc (AB, AC, AI, AJ) est un faisceau harmonique et [B, C, I, J] est une division harmonique.
Télécharger la figure GéoPlan bissect2.g2w
2.d. Quadrilatère complet
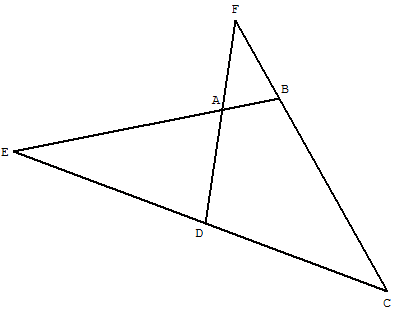
Définition : un quadrilatère complet est formé de quatre droites du plan se coupant, deux à deux, en six points.
Dans la suite de cet article nous considérons le quadrilatère complet strict où deux quelconques des quatre droites ne sont pas parallèles, trois quelconques ne sont concourantes :
A, B, C et D sont quatre points du plan formant un quadrilatère convexe (qui n'est pas un trapèze), les droites (AB) et (CD) se coupent en E, puis (AD) et (BC) en F.
Les quatre droites (AB), (AD), (CB) et (CD) déterminent un quadrilatère complet ayant les six sommets A, B, C, D, E et F.
Les trois droites (AC), (BD) et (EF) sont les diagonales du quadrilatère complet, leurs points d'intersection I, J, K sont les points diagonaux.
Figure interactive dans GeoGebra Tube : quadrilatère complet
2.e. Divisions harmoniques du quadrilatère complet
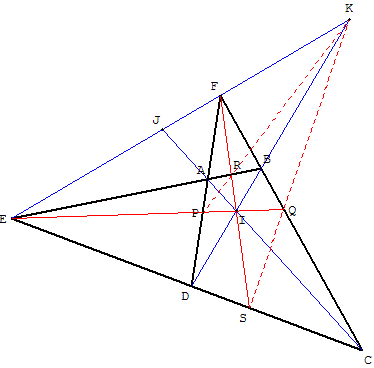
Deux côtés, la diagonale passant par leur point d'intersection et la droite joignant ce sommet au point d'intersection des deux autres diagonales forment un faisceau harmonique.
Par exemple, la droite (FI) est la polaire de E par rapport aux droites (FD), (FC).
(FD), (FC), (FE), (FI) est un faisceau harmonique.
[A, B, E, R] ; [P, Q, E, I] et [D, C, E, S] sont des divisions harmoniques.
(EI) est la polaire de F par rapport à (EB), (EC).
(EB), (EC), (EF), (EI) est aussi un faisceau harmonique.
[A, D, F, P] ; [R, S, F, S] et [B, C, F, Q] sont des divisions harmoniques.
Les points K, R, P sont alignés ; de même, les points K, Q, S sont aussi alignés.
Figure interactive dans GeoGebra Tube : Divisions harmoniques du quadrilatère complet
Feuille de travail dynamique avec GeoGebra
WikiPédia : quadrilatère complet
3. Conjugués harmoniques par rapport à un cercle
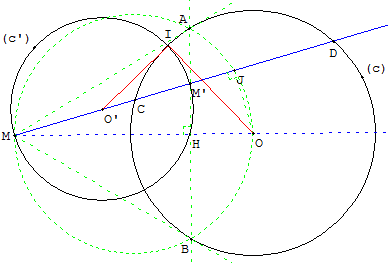
On dit que deux points M et M’ sont conjugués harmoniques par rapport à un cercle (c)
si la droite (MM’) rencontre le cercle (c) en deux points C et D
tels que la division [M, M’, C, D] soit harmonique.
Une droite passant par M coupe le cercle (c) de centre O en C et D.
Soit J le milieu de [CD]. J est la projection orthogonale de O sur la corde [CD].
D'après la formule de Mac-Laurin le conjugué M’ de M par rapport à C et D vérifie MM’ × MJ = MC × MD.
Le cercle (c’) de diamètre [MM’] est orthogonal au cercle (c).
Par extension, on dit que deux points M et M’ sont conjugués harmoniques par rapport à un cercle (c) si le cercle de diamètre [MM’] est orthogonal au cercle (c).
Télécharger la figure GéoPlan conjugue_cercle.g2w
4. Polaire d'un point par rapport à un cercle
Polaire d'un point M par rapport à un cercle : droite définie comme l'ensemble des points M’ conjugués harmoniques de M par rapport au cercle.
Construction à la règle seule
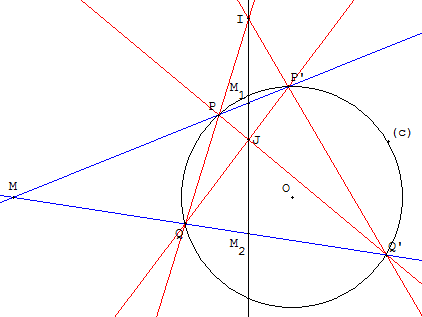
On applique la méthode de construction de la polaire par rapport à deux droites.
D'un point M, tracer deux sécantes au cercle (MP) et (MQ) qui recoupent le cercle respectivement en P’ et Q’.
On obtient le quadrilatère complet MPP’Q’QI. Ses diagonales (PQ’) et (P’Q) se coupent en J. La droite (IJ) est la polaire de M par rapport à (d) et (d’).
La droite (IJ) coupe (MP) en M1 et (MQ) en M2.
Comme M1 est le conjugué de M par rapport à P et P’; les points M et M1 sont conjugués par rapport au cercle (c).
De même, M2 est le conjugué de M par rapport à Q et Q’ ; les points M et M2 sont conjugués par rapport au cercle (c).
La droite (IJ) est la polaire de M par rapport au cercle (c).
Télécharger la figure GéoPlan polaire_cercle_d.g2w
Utilisation des tangentes au cercle
Point M à l'extérieur du cercle
Soit M un point à l'extérieur d'un cercle (c) de centre O. Les tangentes issues de M coupent le cercle en A et B. La droite (AB) est la polaire de M par rapport à (c).
Construction d'Euclide : les points A et B sont les points d'intersection du cercle (c) et du cercle de diamètre [MO].
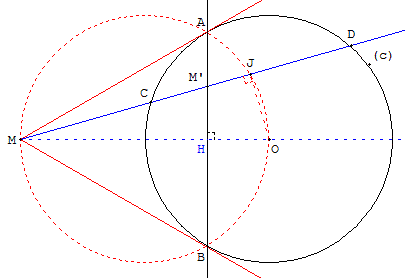
Démonstration : soit M’ un point du segment [AB]. La droite (MM’) coupe le cercle (c) en C et D.
La puissance du point M par rapport au cercle (c) est MC × MD = MA2.
Soit H le milieu de [AB], point d'intersection des droites (AB) et (MO), et α l'angle des droites (MO) et (MM’).
Dans le triangle rectangle MHM’, on a MM’ = MH/cos α.
Dans le triangle rectangle MOJ, MJ = MO cos α.
De ces deux dernières égalités on déduit MM’ × MJ = MH × MO.
Dans le triangle rectangle MAO; le côté MA de l'angle droit est moyenne proportionnelle entre l'hypoténuse MO et sa projection sur l'hypoténuse MH :
MA2 = MH × MO.
D'où MM’ × MJ = MC × MD d'après la relation de Mac-Laurin M et M’ partagent harmoniquement [CD].
M’ est un point la polaire de M.
Télécharger la figure GéoPlan polaire_cercle.g2w
Point M à l'intérieur du cercle
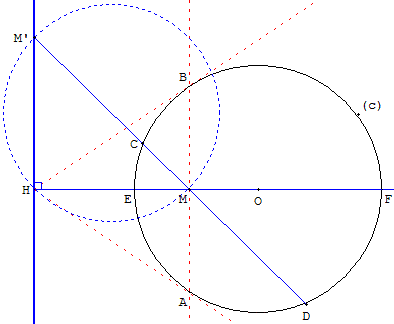
La perpendiculaire en M à (OM) rencontre le cercle en A et B.
Les tangentes au cercle en A et B et la droite (OM) sont concourantes en H.
La polaire de M est la droite (d) perpendiculaire en H à (OM).
Rappel : une condition nécessaire et suffisante pour que deux cercles soient orthogonaux, est qu'il existe un diamètre de l'un d'entre eux qui soit divisé harmoniquement par l'autre cercle.
Démonstration : Une droite quelconque passant par M rencontre le cercle (c) en C et D.
Soit M’ le point conjugué harmonique de M par rapport à C et D.
Le cercle (c’) de diamètre [MM’] est orthogonal à (c).
Le cercle (c’) divise harmoniquement le diamètre [EF] du cercle (c).
Mais comme M est sur la polaire de H par rapport à (c), M et H sont conjugués harmoniques par rapport à E et F.
Le deuxième d'intersection du cercle (c’) avec (OM), conjugué harmonique de M est donc le point H.
Le triangle M’HM, inscrit dans un demi-cercle, est rectangle. Le point M’ est sur la perpendiculaire en H à (OM).
Télécharger la figure GéoPlan polaire_cercle_2.g2w
Conclusion : soit un point M distinct de O, l'ensemble des points M’ conjugués harmoniques de M par rapport à un cercle c(O, R) est une droite (d) appelée polaire de M par rapport à (c). Le point M est le pôle de (d) par rapport à (c).
La polaire de M est la droite perpendiculaire à (OM) au point H de [OM) tel que OH × OM = R2.
Réciprocité polaire : si la polaire (d) de M passe par M’, alors la polaire (d’) de M’ passe par M.
Les points M et M’ sont conjugués par rapport au cercle.
Les droites (d) et (d’) sont conjuguées par rapport au cercle.
Polaires de l'orthocentre au cercle circonscrit et au cercle d'Euler
Étant donné un cercle (c), dit directeur, on appelle ainsi la transformation qui :
– à tout point M, fait correspondre la polaire de M par rapport à (c) ;
– à toute droite (d), fait correspondre le pôle de (d) par rapport à (c).
Par l'association pôle/polaire, à une figure (γ) formée de points et de droites, on fait correspondre une figure (Γ) formée de droites et de points.
Si quatre points forment une division harmonique, leurs transformés forment un faisceau harmonique et réciproquement.
La « polarisation » échange les notions de droites concourantes et de droite passant par deux points :
deux droites et leur point d'intersection sont transformées en deux points (les deux pôles) et une droite (la polaire du point d'intersection, joignant ces deux points) et réciproquement.À toute propriété d'alignement de points ou de concours de droites dans (γ), correspond une propriété corrélative de concours de droites ou d'alignement de points dans (Γ).
Les propriétés d'angles ou de distances ne se conservent pas ;
toutefois quand deux droites sont perpendiculaires, les points transformés sont vus du cercle directeur sous un angle droit et vice versa.
Si un point M se déplace sur courbe (γ), les polaires (d) de M sont tangentes à une courbe polaire (Γ), enveloppe de ces polaires ;
la polaire (Γ) est aussi le lieu des pôles des tangentes à la courbe (γ) : les polaires, transformées des points de (Γ), sont les tangentes à la courbe (γ).
La courbe (γ) et sa polaire (Γ) sont réciproques l'une de l'autre, d'où l'appellation « transformation par polaires réciproques ».
5. Transformation des médianes d'un triangle
Soit un triangle ABC. Prenons pour cercle directeur le cercle (c) circonscrit à ABC de centre O.
Les sommets ABC ont pour transformés les tangentes à (c) en A, B et C, formant le triangle tangentiel A1B1C1, circonscrit à ABC.
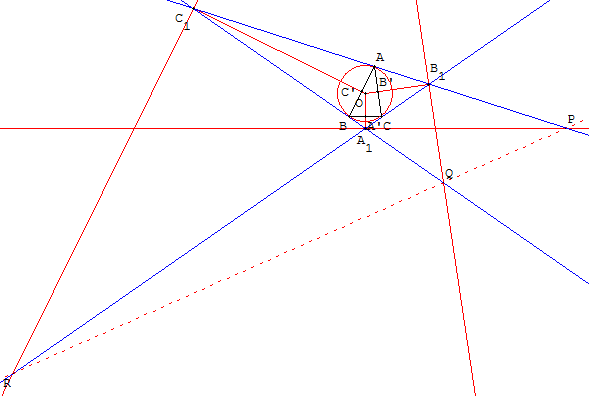
La médiane AA’ se transforme en un point P. P est situé sur la tangente (B1C1), transformée de A, et P est situé sur la polaire (d1) de A’ qui est la droite parallèle à (BC) passant par A1, droite qui est perpendiculaire à (OA1).
Q pôle de BB’ est le point d'intersection de (A1C1) et de la polaire (d2) de B’ : la droite parallèle à (AC) passant par B1,
R pôle de CC’ est le point d'intersection de (A1B1) et de la polaire (d3) de C’ : la droite parallèle à (AB) passant par C1.
Le concours des médianes se transforme en l'alignement des points P, Q et R.
Bissectrices extérieures du triangle tangentiel
Le point O, centre du cercle (c) inscrit dans le triangle tangentiel A1B1C1, est le point de concours des bissectrices intérieures (A1O), (B1O),
(C1O). Les droites (d1), (d2), (d3), respectivement perpendiculaires à ces bissectrices intérieures, sont les bissectrices extérieures du triangle tangentiel A1B1C1.
Ce triangle A1B1C1 est quelconque. On peut donc énoncer :
Dans tout triangle (non équilatéral), les bissectrices extérieures coupent les côtés opposés en trois points alignés (pour un triangle isocèle, un des points peut être rejeté à l'infini).
Télécharger la figure GéoPlan polaire_mediane.g2w
6. Transformation des hauteurs d'un triangle
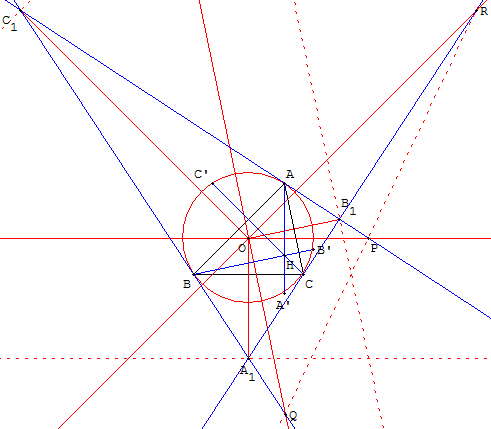
Soit un triangle ABC. Prenons pour cercle directeur le cercle (c) circonscrit à ABC de centre O.
Les sommets ABC ont pour transformés les tangentes à (c) en A, B et C, formant le triangle tangentiel A1B1C1 circonscrit à ABC.
La hauteur (AH) se transforme en un point P situé sur la tangente (B1C1), transformée de A, et sur la perpendiculaire en O à (AH), c'est-à-dire la parallèle à (BC), passant par O, perpendiculaire à la bissectrice intérieure (OA1) de A1B1C1.
Q pôle de (BH) est le point d'intersection de (A1C1) et de la parallèle à (AC), passant par O,
R pôle de (CH) est le point d'intersection de (A1B1) et de la parallèle à (AB), passant par O.
Le concours des hauteurs se transforme en l'alignement des points P, Q et R.
Parallèles aux bissectrices extérieures du triangle tangentiel
Le triangle A1B1C1 est quelconque. On peut donc énoncer :
Dans tout triangle (non équilatéral), les parallèles aux bissectrices extérieures, menées par le centre du cercle inscrit, coupent les côtés opposés en trois points alignés (pour un triangle isocèle, un des points peut être rejeté à l'infini).
Télécharger la figure GéoPlan polaire_hauteur.g2w
Table des matières
Dans d'autres pages du site
Division harmonique Plan projectif
Intersection inaccessible : Polaires réciproques
Épreuve pratique de terminale S
Google friendly
Page no 150, extraite de l'article plan projectif le 3/8/2009