Descartes et les Mathématiques

Construction de triangles

Résolution d'un triangle par la donnée de trois des éléments (côté, hauteur, médiane, rayon du cercle circonscrit…).

Résolution d'un triangle

Classe de première L

En géométrie, la résolution d'un triangle consiste en la détermination des différents éléments d'un triangle (longueurs des côtés, mesure des angles…) à partir de certains autres.

Historiquement, la résolution des triangles fut motivée

• chez les Grecs en géométrie euclidienne, pour la résolution de nombreux problèmes de géométrie ;
• en cartographie, pour la mesure des distances par triangulation ;
• pour le point en navigation, qui utilise des calculs de coordonnées terrestres et astronomiques (trigonométrie sphérique).

La donnée de trois des éléments du triangle (côté, hauteur, médiane, rayon du cercle circonscrit…), dont au moins un côté, est nécessaire et, en général, suffisante à la résolution du triangle. On se pose en particulier le problème de l'unicité, les cas de résolution pouvant admettre plusieurs solutions.

Ces casse-tête géométriques sont en principe toujours solubles, parfois au prix de calculs ardus qui font intervenir les relations classiques dans le triangle comme le théorème d'Al-Kashi, la loi des sinus, la somme des angles et la trigonométrie.

1. Construire un triangle connaissant un côté et le rayon du cercle circonscrit

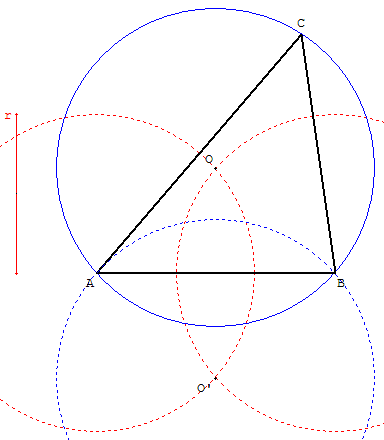
Construire un triangle connaissant le côté [AB] et le rayon r du cercle circonscrit.

Tracer les cercles de centres A et B de rayon r.

Soit O et O’ les points d'intersection de ces deux cercles lorsqu'ils existent (2r > AB).

Les cercles circonscrits sont les cercles (c) et (c’) de centres O et O’ passant par A.

En choisissant n'importe quel point C sur un de ces deux cercles (sauf les points A et B) on obtient une solution.

Télécharger la figure GéoPlan cote_rayon_cir.g2w

2. Construire un triangle connaissant deux côtés et le rayon du cercle circonscrit

Construire un triangle connaissant le côté [AB], la longueur b du côté [AC] et le rayon r du cercle circonscrit.

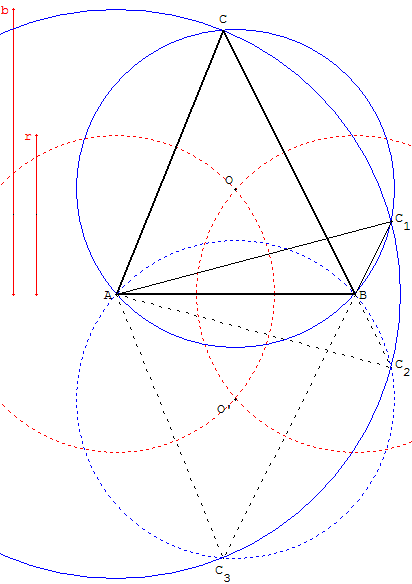
Tracer les cercles de centres A et B de rayon r.

Soit O et O’ les points d'intersection de ces deux cercles,
lorsqu'ils existent (2r > AB).

Les cercles circonscrits sont les cercles (c) et (c’) de centres O et O’ passant par A.

Le cercle, de centre A et de rayon b, peut couper les cercles circonscrits aux points C, C₁, C₂ et C₃, permettant de trouver jusqu'à quatre triangles solutions, symétriques par rapport à (AB).

Télécharger la figure GéoPlan 2cotes_rayon_cir.g2w

3. Construire un triangle connaissant un côté et l'angle opposé

Construire un triangle connaissant le côté [BC] et l'angle BÂC = xÎy.

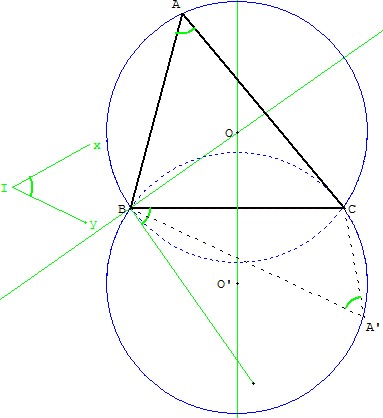
Reporter l'angle xÎy le long de [BC) et on trouve une tangente au cercle circonscrit.

La perpendiculaire en B à cette tangente rencontre la médiatrice de [BC] en O, centre du cercle circonscrit.

Le point A appartient aux arcs capables,
d'où l'on « voit » le segment [BC] suivant l'angle xÎy.

Télécharger la figure GéoPlan cote_angle.g2w

4. Construire un triangle connaissant un côté et deux médianes

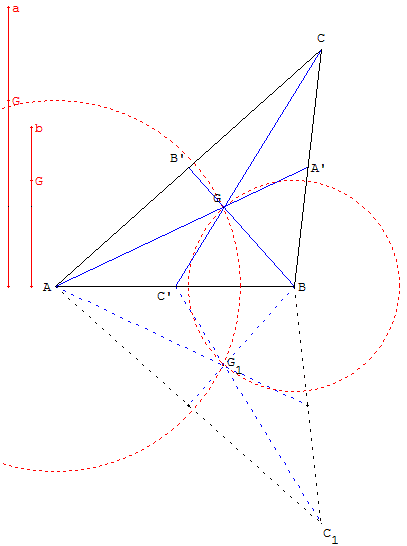
Construire un triangle connaissant un côté [AB] et les longueurs a et b des deux médianes issues de A et B.

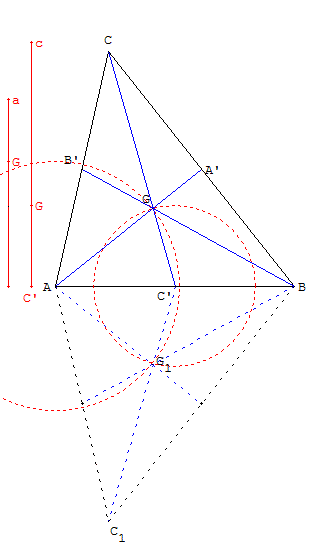
Le centre de gravité G du triangle ABC est un des points d'intersection, lorsqu'il existe, des cercles de centre A, de rayon a et de centre B, de rayon b.

Télécharger la figure GéoPlan cote_2medianes_a.g2w

Construire un triangle connaissant un côté [AB] et les longueurs a et c des deux médianes issues de A et C.

Le centre de gravité G du triangle ABC est un des points d'intersection des cercles de centre A, de rayon a et de centre C’, milieu de [AB], de rayon c.

Télécharger la figure GéoPlan cote_2medianes_b.g2w

5. Construire un triangle connaissant un côté et deux hauteurs

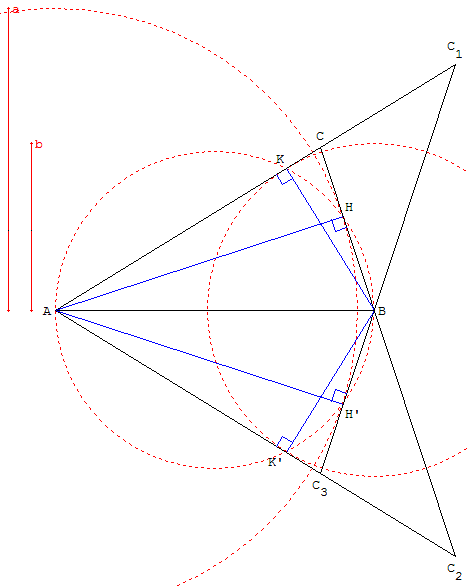
Construire un triangle connaissant un côté [AB] et les longueurs a et b des deux hauteurs issues de A et B.

Le pied H de la hauteur issue de A est un des points d'intersection, lorsqu'il existe, du cercle de diamètre [AB] et du cercle de centre A et de rayon a.
De même, le pied K de la hauteur issue de B est une des intersections du cercle de diamètre [AB] et du cercle de centre B et de rayon b.

Le sommet C est l'intersection des côtés (AK) et (BH). Il y a jusqu'à quatre solutions symétriques, deux à deux, par rapport à (AB).

Télécharger la figure GéoPlan cote_2hauteurs_a.g2w

Construire un triangle connaissant un côté [AB] et les longueurs b et c des deux hauteurs issues de B et C.

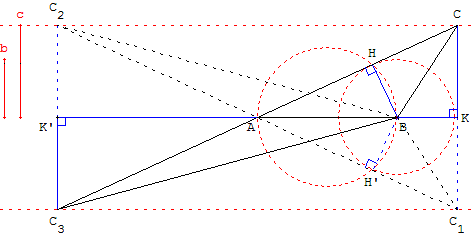
Le pied H de la hauteur issue de B est un des points d'intersection, lorsqu'il existe, du cercle de diamètre [AB] et du cercle de centre B et de rayon b.

Le sommet C est l'intersection du côté (AH) et d'une des parallèles à (AB) située à une distance c de (AB).

Il y a jusqu'à quatre solutions symétriques, deux à deux, par rapport à (AB).

Télécharger la figure GéoPlan cote_2hauteurs_b.g2w

Extrait de l'ancien programme de quatrième (2007)