 Descartes et les Mathématiques
Descartes et les Mathématiques
Optimisation en classe de seconde
Ce qui aurait pu être des contenus pour l'enseignement de mathématiques.
Sommaire
Quels problèmes au lycée ?
Exemples de contenu de TP pour la seconde
Exemples de TP d'optimisation
1. Stade constitué d'une pelouse rectangulaire
Maximisation de volume avec une surface minimale
2. La casserole
Calcul d'aire
Quels problèmes au lycée ?
Document d'accompagnement 2nde 2009
Deux familles de problèmes :
• type no1 : un problème se ramenant à une équation du type f (x) = k (fonction donnée ou non),
• type no2 : un problème d'optimisation ou du type « f (x) > k » (résolution exacte ou approchée, graphique ou algébrique).
Dans les deux cas, toute autonomie peut être laissée pour associer au problème une fonction.
Comment ?
• Identifier deux quantités qui varient tout en étant liées.
• Expliciter le lien entre ces deux quantités de diverses manières (tableau de valeurs, nuage de points, courbe, formule).
• Identifier les avantages et les inconvénients de tel ou tel aspect d'une fonction – tableau de valeurs, nuage de points, courbe, formule – selon la question initialement posée.
Un exemple : optimisation d'aires
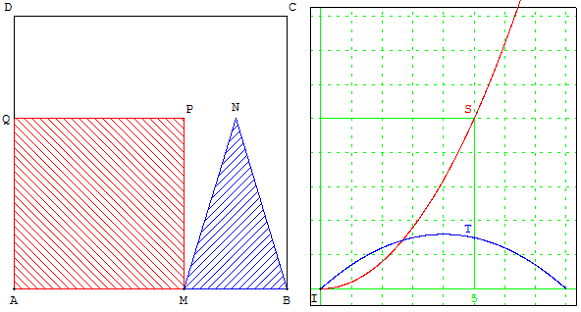
Une même situation pour divers problèmes
Le carré ABCD a un côté de longueur 8 cm.
M est un point du segment [AB]. On dessine comme ci-dessus dans le carré ABCD un carré de côté [AM] un triangle isocèle de base [MB] et dont la hauteur a même mesure que le côté [AM] du carré.
On s'intéresse aux aires du carré, du triangle, du motif constitué par le carré et le triangle :
• Problème du type no1 : On voudrait que le motif ait une aire égale à la moitié de celle du carré ABCD.
Quelles dimensions faut-il donner au motif ?
• Problème du type no1 : Est-il possible que l'aire du triangle soit égale à l'aire du carré ? (AM = 8/3)
• Problème du type no2 : Est-il possible de faire en sorte que l'aire du triangle soit la plus grande possible ? Si oui, préciser dans quel(s) cas ?
• Problème du type no2 : Est-il possible de faire en sorte que l'aire du triangle soit plus grande que l'aire du carré ?
Si oui, préciser dans quels cas c'est possible.
• Problème du type no2 : Comment évolue l'aire du motif en fonction de AM ? En fonction de MB ?
![]() Figure interactive dans GeoGebraTube : optimisation des aires d'un carré et d'un triangle
Figure interactive dans GeoGebraTube : optimisation des aires d'un carré et d'un triangle
![]() Feuille de travail dynamique avec GeoGebra
Feuille de travail dynamique avec GeoGebra
Exemples de contenu de TP pour l'enseignement de mathématiques dans la nouvelle seconde
Thèmes de la consultation nationale
Ces contenus ont été rédigés avant que l'on connaisse les thèmes proposés par la consultation nationale du projet de programme de mathématiques de seconde pour 2009-2010.
Ces thèmes sont :
1. Cryptologie et codage
2. Utilisations de la théorie des graphes
3. Phénomènes d'évolution
Aucun thème de géométrie n'est proposé, effectivement que faire avec uniquement des droites ?
Malgré tout, notons de façon positive que :
« L'entrée dans le thème doit privilégier une activité de recherche et d'expérimentation autour d'un questionnement.
Les problèmes étudiés doivent combiner des activités de recherche, d'expérimentation – notamment avec des outils logiciels –, de raisonnement, de communication et doivent permettre de mettre en œuvre, selon le thème, des méthodes
variées : numériques, graphiques, géométriques, logiques ou algorithmiques.
…
L'évaluation peut prendre en compte, par exemple : la réalisation et la présentation d'un programme informatique. »
Programme de géométrie
Presque vide, uniquement des droites dans le plan (au vu de ces programmes, on regrette que Descartes ait inventé l'analytique). Une performance : pratiquement impossible à réaliser avec Cabri !
Finis les configurations du triangle, les transformations et les vecteurs.
Sans géométrie dans l'espace, « il s'agit aussi renforcer la vision dans l'espace des élèves ». Comment ?
1. Le stade
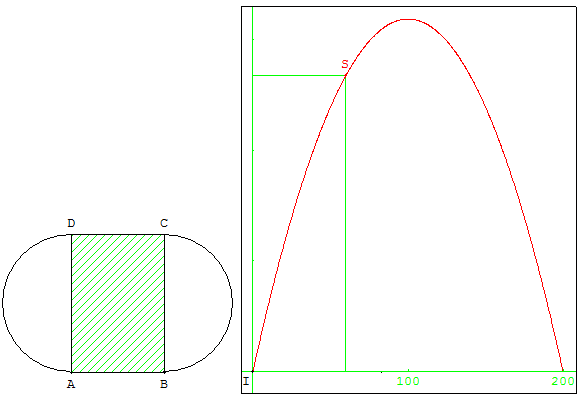
Utilisation de deux cadres dans GéoPlan : un pour visualiser une situation géométrique, l'autre pour tracer une fonction.
Optimisation de la surface d'un stade
Un stade est constitué d'une pelouse centrale rectangulaire ABCD, complétée par deux demi-disques de diamètre [AD] et [BC]. Ce terrain est entouré par une piste de course à pied de longueur égale à 400 m.
Quelles doivent être les dimensions du rectangle ABCD si l'on veut que son aire soit maximale ?
![]() Télécharger la figure GéoPlan stade.g2w
Télécharger la figure GéoPlan stade.g2w
Indications
Les élèves donnent les noms l à la longueur AB et r au rayon des demi-cercles.
Le périmètre vaut : 2 l + 2π r = 400.
Ce qui permet d'en déduire soit : |
l = 200 − π r, |
soit |
r = (200 − l) / π, |
et fournit l'aire à optimiser soit sous la forme |
A = 2 l (200 – l) / π, |
soit sous la forme |
A = 2 (200 − π r) r. |
Le maximum est atteint pour |
l = 100 m |
ou pour |
r = 100/ π. |
Les pistes de course à pied sont bien construites ainsi : deux lignes droites de 100 m, et deux « virages » de 100 m.
Le terrain de foot central a alors une aire maximale.
Maximisation de volume avec une surface minimale
2. La casserole
Optimisation du volume d'une casserole
Pourquoi les batteries de casseroles que l'on trouve dans le commerce sont-elles toutes du même type ? Prenons par exemple la casserole de deux litres. Pourquoi a-t-elle à peu près 9 cm de haut pour un diamètre de 17 cm quelle que soit la marque achetée ?
La tôle d'une casserole coûte cher ! Pour minimiser son coût de fabrication, il faut minimiser la quantité de métal utilisée et donc l'aire de la casserole.
Montrer que pour un volume V donné, la casserole « économique » est celle dont le rayon est égal à la hauteur.
Indications
On nomme h la hauteur du cylindre, r son rayon.
À volume V fixé, on cherche les valeurs de r et h telles que l'aire du fond et du côté du cylindre soit minimale.
Il suffit d'exprimer le volume en fonction de r et h : V = πr2h,
de calculer h dans cette formule : h = V/(πr2).
Puis exprimer l'aire A en fonction de r et h : A = πr2 + 2πrh.
On substitue h pour exprimer l'aire en fonction de r et du volume V : A = πr2 + 2V/r.
En classe de première, on utilise la dérivée A’ = dA/dr : A’ = 2πr - 2V/r2 = (2πr3 - 2V)/r2.
L'aire est extrémale lorsque A’ s'annule : on obtient donc une relation entre r et V : 2πr3 - 2V = 0, soit r3 = V/π.
Mais comme d'après le calcul du volume V/π = πr2h, on a : h = r.
On a donc r = h = (V/π)^(1/3).
En classe de seconde, on fixe une valeur du volume V, par exemple 2000 cm3. On peut travailler avec un grapheur ou une calculatrice où les modèles, même les plus simples, fournissent les coordonnées des extrema avec une grande précision.
On peut aussi utiliser un tableur avec un pas de 1, puis de 0,1 :
Dans la case B1, taper le volume 2000.
Ligne 3, dans les cases B3 et C3 taper 1 et 2, sélectionner ces deux cases et les tirer vers la droite jusqu'a 10.
Ligne 4 dans la case B4 introduire la formule
=PI()*B3^2+2*$B$1/B3
en écrivant des $B$1 pour que le volume B1 soit une case absolue. Déplacer cette formule vers la droite.
Le minimum est entre 8 et 9, les deux plus petites valeurs de A.
Recommencer ligne 3, dans les cases B3 et C3 taper 8 et 8.1, sélectionner ces deux cases et les tirer vers la droite jusqu'a 9.
| V= | 2000 |
| r | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pi r^2+2V/r | 4003 | 2013 | 1362 | 1050 | 879 | 780 | 725 | 701 | 699 | 714 |
| r | 8 |
8.1 |
8.2 |
8.3 |
8.4 |
8.5 |
8.6 |
8.7 |
8.8 |
8.9 |
9 |
| pi r^2+2V/r | 701.1 | 699.9 | 699.0 | 698.4 | 697.9 | 697.6 | 697.5 | 697.6 | 697.8 | 698.3 | 698.9 |
On obtient une casserole de 8,6 cm de hauteur, et de diamètre 17,2 cm.
Ce sont bien les dimensions intérieures d'une casserole ordinaire.
Télécharger le fichier Excel casserole.xls
3. La boite de maïs
Une variante du problème précédent est fournie par l'optimisation des dimensions d'une boite de maïs.
Pourquoi de maïs ? Les boites de conserve ordinaires, disons de petits pois, n'ont pas des dimensions optimisées. Mais le maïs est conservé sous vide, et requiert donc une tôle plus épaisse que les autres boites. Les industriels ont donc optimisé les dimensions pour réduire le coût.
On impose un volume V donné et le même genre de calculs conduit dans ce cas à la boite « économique » dont le diamètre est égal à la hauteur.
C'est bien le cas des boites de maïs usuelles.
Indications
On nomme h la hauteur du cylindre, r son rayon.
À volume V fixé, on cherche les valeurs de r et h telles que l'aire du cylindre soit minimale.
Il suffit d'exprimer le volume en fonction de r et h : V = πr2h,
de calculer h dans cette formule : h = V/(πr2).
Puis exprimer l'aire A en fonction de r et h : A = 2πr2 + 2πrh.
On substitue h pour exprimer l'aire en fonction de r et du volume V : A = 2πr2 + 2V/r.
En classe de première, on utilise la dérivée A’ = dA/dr : A’ = 4 πr - 2V/r2 = (4πr3 - 2V)/r2.
L'aire est extrémale lorsque A’ s'annule : on obtient donc une relation entre r et V : 4 πr3 - 2V = 0, soit r3 = V/(2π).
Mais comme d'après le calcul du volume V/π = πr2h, on a : h = 2r.
On a donc 2r = h = {V/(2π)}^(1/3).
En classe de seconde, voir ci-dessus pour l'utilisation de moyens de calcul.
4. Partage en deux d'un trapèze rectangle
ABCD est un trapèze rectangle de grande base [AB].
Trouver un point M du segment [AB] tel que [CM] partage le trapèze ABCD en deux parties d'aires égales.
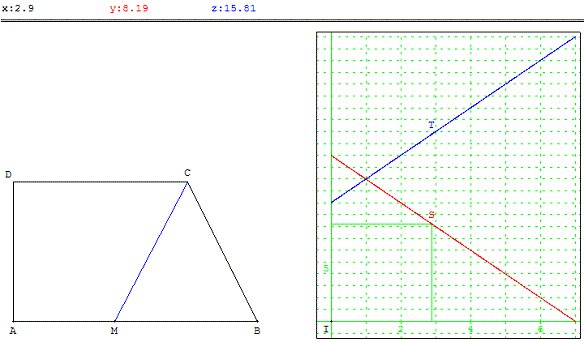
On note :
• x la longueur AM
• f(x) l'aire du triangle CMB
• g(x) l'aire du trapèze AMCD.
Le graphique de droite représente ces deux aires en fonction de x.
En vous aidant du graphique, retrouvez la position du point M.
![]() Télécharger la figure GéoPlan trapeze.g2w
Télécharger la figure GéoPlan trapeze.g2w
Indications : cas particulier AB = 7 et DC = 5
AB = b = 7, AM = x, DC = c = 5, AD = h = 4.
L'aire du triangle CMB est ![]() MB × AD =
MB × AD = ![]() (b - x)× h.
(b - x)× h.
L'aire du trapèze AMCD est ![]() (AM + CD) × AD =
(AM + CD) × AD = ![]() (x + c) × h.
(x + c) × h.
f(x) = 2(7 - x) et g(x) = 2(x + 5). L'égalité des aires est vérifiée pour x = 1.
Cas général AB = b et DC = c
On trouve x = (b − c)/2. La solution est indépendante de la hauteur du trapèze.
5. Autre partage d'un trapèze rectangle
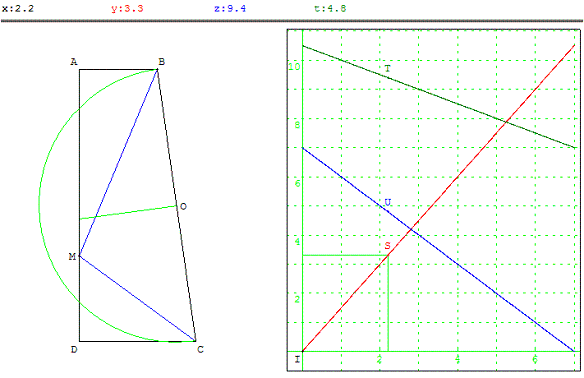
ABCD est un trapèze rectangle de bases [AB] et [CD] et de hauteur [AD] tel que AB = 2, AD = 7 et DC = 3.
M est un point mobile du segment [AD].
On appelle T1 le triangle DMC ; T2 le triangle BCM et T3 le triangle ABM.
Partie 1
a. Trouver la position de M pour que l'aire de T1 soit égale à ![]() (touche 1 avec GéoPlan).
(touche 1 avec GéoPlan).
b. Dans ce cas préciser la nature de T2, justifier.
c. Y a-t-il une autre position de M pour que T2 soit de même nature ? (touche 2 avec GéoPlan)
Partie 2
Déterminer toutes les positions de M pour que :
a. Aire(T3) < Aire(T1)
b. Aire(T1) < Aire(T2)
c. Aire(T3) < Aire(T1) < Aire(T2)
Partie 3
Peut-on trouver M sur [AD] pour que T2 soit isocèle en M ? (touche 3 avec GéoPlan)
![]() Télécharger la figure GéoPlan trapeze2.g2w
Télécharger la figure GéoPlan trapeze2.g2w
Table des matières
Dans d'autres pages du site
Menu optimisation
1ère S : Problèmes d'optimisation
La géométrie en seconde
Plus court chemin Fonctions distance
![]() Aire délimitée par un périmètre de baignade
Aire délimitée par un périmètre de baignade
![]() Aire minimale de deux carrés dans un carré
Aire minimale de deux carrés dans un carré
![]() Aire minimale d'un triangle inscrit dans un rectangle
Aire minimale d'un triangle inscrit dans un rectangle
Quels contenus pour l'enseignement des mathématiques au lycée
Exemples de TP pour l'enseignement de mathématiques en seconde
Carré et triangles équilatéraux - Prouver des alignements
Le plus grand rectangle inscrit dans un triangle rectangle
Le plus grand rectangle inscrit dans un triangle isocèle
Le plus grand triangle isocèle inscrit dans un cercle
Algorithme de Babylone : pourquoi une telle vitesse ?
Volume maximal d'un cylindre inscrit dans un cône
Capes : recherche d'extremum
![]() Google friendly
Google friendly
|
|
Page no 139, créée le 24/3/2009 |