Descartes et les Mathématiques

Optimisation en classe de troisième

Aire maximale d'un triangle

De nombreuses situations menant à des problèmes d'optimisation :
à partir de figures géométriques, études de longueurs ou d'aires
et recherche d'extrema.

Sommaire

1. Aire maximale de triangles de périmètre constant
    a. Aire de triangles de base et périmètre constant
    b. Aire de triangles isocèles de périmètre constant
2. Aire maximum d'un triangle

3. Le plus petit triangle

4. L'hypoténuse variable

5. Aire maximale d'un rectangle de diagonale constante

Technique GéoPlan : dans plusieurs exercices de cette page est utilisée une seule figure avec deux cadres : le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction.

Isopérimétrie

Problème issu du mythe de la reine Didon lors la création de Carthage :
trouver la forme géométrique qui maximise son aire avec un périmètre fixé.

1. Aire maximale de triangles de périmètre constant

Objectif

À l'aide d'un logiciel de géométrie dynamique, approcher la notion de fonction par la représentation graphique de l'aire d'un triangle.

Pour un périmètre constant, la recherche d'un triangle d'aire maximale se fait en deux étapes. Dans un premier temps, en supposant la base de longueur constante, on montre que le triangle d'aire maximale est isocèle. Dans une deuxième étape, à partir d'un triangle isocèle, on montre que l'aire est maximale pour un triangle équilatéral.

Ces études sont à envisager en classe de troisième ou seconde. En classe de première ou terminale, il est possible d'expliciter les fonctions et de réaliser leur étude. Pour la classe de troisième, il est conseillé de sauter la première étape et de ne faire que l'étude pour des triangles isocèles.

Le résultat établi est que, pour périmètre donné, c'est le triangle équilatéral qui a l'aire maximale.

1.a. Aire de triangles de base et périmètre constant

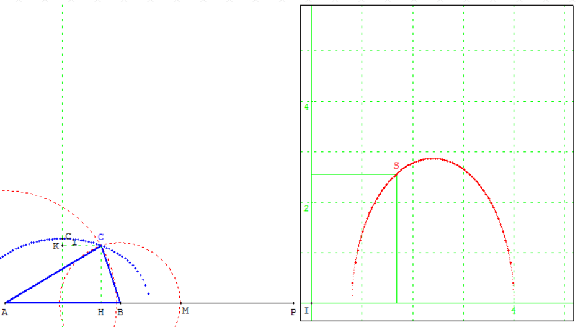
Étudier comment varie l'aire d'un triangle de base et de périmètre constant.

Travaux pratiques

On considère un triangle ABC, de base [AB] fixe et de périmètre fixe égal à une longueur AP.

Choisir un point M variable sur le segment [BP] et tracer, lorsque cela est possible, le triangle ABC de côté BC = BM et AC = MP.
On représente, en fonction de x = BM, l'aire y du triangle ABC.

Télécharger la figure GéoPlan aire_triangle_1.g2w

Solution

L'aire est égale à AB × CH. Elle est maximale lorsque CH maximale. Le maximum est atteint lorsque M est au milieu de [BP], le point C est alors en C₁, situé sur la médiatrice de [AB], c'est-à-dire lorsque ABC est un triangle isocèle.

En classe de première, on remarque que comme AC + CB est constant, égal à BP, le point C est situé sur une ellipse. Le sommet C₁ rend maximum la hauteur CH.

1.b. Aire de triangles isocèles de périmètre constant

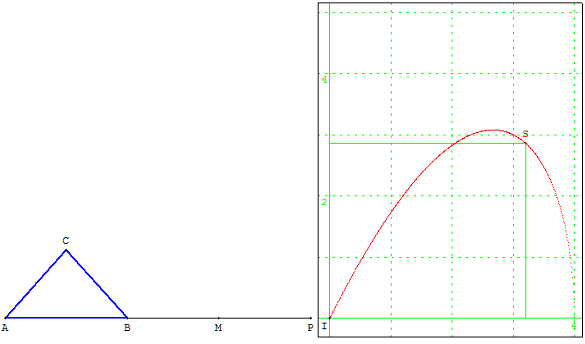
Maximiser l'aire d'un triangle à périmètre constant.

Étudier comment varie, en fonction de la base, l'aire d'un triangle isocèle de périmètre constant.

On considère un triangle ABC isocèle en C, de base [AB] et de périmètre fixe, égal à la longueur BP.

À partir du milieu M de [CP], construire le point C, intersection du cercle de centre B, passant par M, avec la médiatrice de [AB].

On représente, en fonction de x = AB, l'aire y du triangle ABC et l'on fait varier le point B.

Télécharger la figure GéoPlan aire_triangle_2.g2w

Solution

L'aire maximale est atteinte pour un point B situé au tiers de [AP], c'est-à-dire pour un triangle équilatéral.

2. Aire maximum d'un triangle

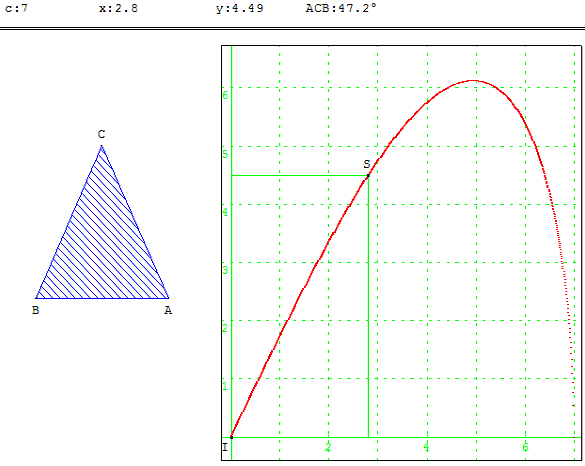
Maximiser l'aire d'un triangle isocèle.

Le triangle ABC de base [AB] variable, isocèle au sommet C, a deux côtés de longueur fixe c telle que AC = BC = c (ici c est initialisé à 7).
Peut-on construire un triangle isocèle d'aire maximum ?

Utilisation du logiciel GéoPlan

L'intérêt est de visualiser comment l'aire du triangle varie, en fonction de la longueur de la base.
Le point A est libre ; x la demi-base , y est l'aire A(x) du triangle ABC. Dans le cadre est représenté le point S(x, y).

Solution (lycée)

L'aire A(x) du triangle ABC demi-produit de la base AB par la hauteur AH est donnée par la fonction :

A(x) = = ,       x ∈ [0, 10].

L'aire du triangle est aussi égale à = .

Cette aire est maximale lorsque sin C est maximal, c'est-à-dire lorsque l'angle ACB est droit.

Le maximum correspond à un triangle rectangle isocèle. L'hypoténuse 2x est alors égale c, soit x = c.

Télécharger la figure GéoPlan max_aire_triangle.g2w

3. Le plus petit triangle

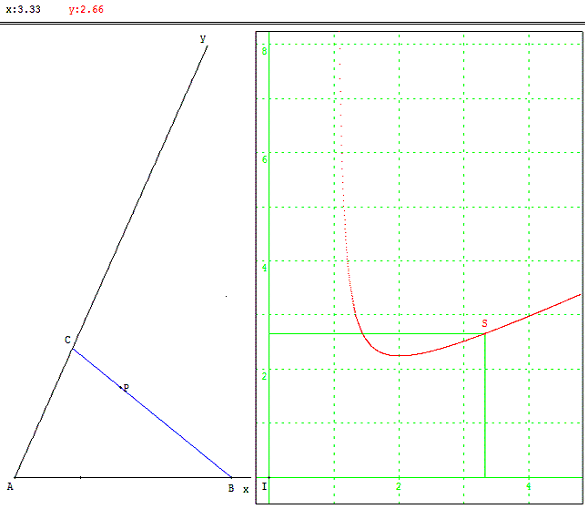
On fixe deux demi-droites formant un angle aigu en A, ainsi qu'un point P à l'intérieur du secteur angulaire qu'elles délimitent.
Une droite variable passant par le point P coupe les deux demi-droites en B et C.

Comment choisir cette droite de façon à rendre minimale l'aire du triangle ABC ?

Le triangle minimal est obtenu lorsque P est le milieu de BC.

Télécharger la figure GéoPlan plus_petit_triangle.g2w

Preuve

On construit le symétrique D du point A par rapport à P et le parallélogramme AB’DC’ de centre P ayant les deux demi-droites [Ax) et [Ay) comme côtés.
Le triangle AB’C’ formé de deux côtés et d'une diagonale est minimal.

En appelant B₁ le deuxième point d'intersection d'une autre sécante (BC) avec le parallélogramme, on compare, dans la configuration de la figure ci-dessus, les triangles ABC et AB’C’.
Les triangles PB’B₁ et PC’C, symétriques par rapport à P, sont égaux.
Le triangle B’B₁B représente l'excédent de l'aire du triangle ABC par rapport à AB’C’.

AB’C’ est le triangle d'aire minimale.

4. L'hypoténuse variable

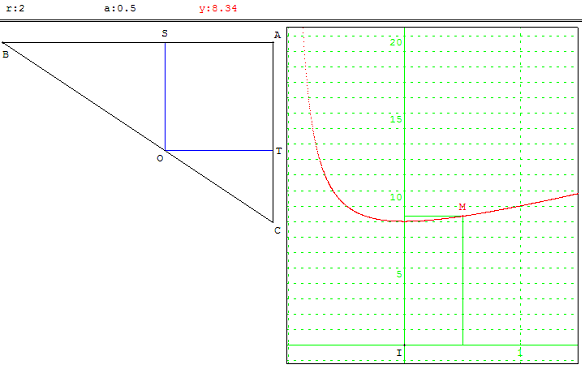
On considère tous les triangles rectangles ABC dont les côtés de l'angle droit prolongent ceux du carré (fixe) ASOT de côté r et dont l'hypoténuse passe par O.
Parmi eux, quel est le triangle d'aire minimum ?
Quelle est cette aire ?

Comme on pouvait s'y attendre, par raison de symétrie, le triangle d'aire minimum est le triangle rectangle isocèle construit autour du carré.
Son aire est égale à 2 r².

Télécharger la figure GéoPlan hypothenuse_variable.g2w

Solution algébrique (lycée)

Appelons t la tangente de l'angle ACB égale au rapport = .

L'aire du triangle ABC est égale à A = (2 + t + ).

On posant t = 1 + a,
t + = 1 + a + = = 2 + et A = 2 r² + .
Il est clair que la valeur minimale est obtenue pour a = 0, soit t = 1 = tan(ACB), d'où ACB = 45°.

Solution géométrique

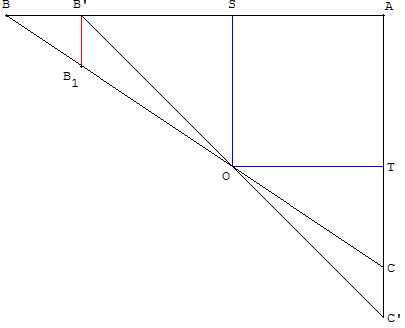
Si ABC est un triangle rectangle dont l'hypoténuse passe par O et AB’C’ le triangle rectangle isocèle construit autour du carré.

Dans la configuration de la figure ci-contre, on appelle B₁ le symétrique de C par rapport à O.

Les triangles OB’B₁ et OC’C, symétriques par rapport à O, sont égaux.
Le triangle BB₁B’ représente l'excédent de l'aire du triangle ABC par rapport à AB’C’.

AB’C’ est le triangle d'aire minimale.

Télécharger la figure GéoPlan hypotenuse_variable_geo.g2w

5. Aire maximale d'un rectangle de diagonale constante

L'aire d'un rectangle de diagonale donnée est inférieure à l'aire du carré de même diagonale.

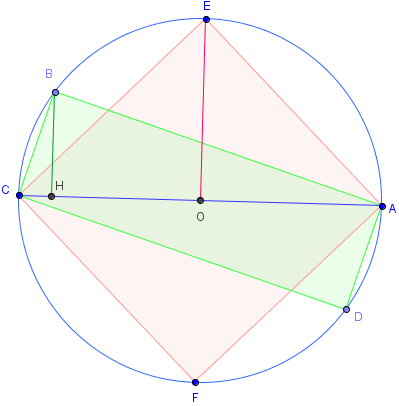
Soit ABCD est un rectangle de diagonale [AC] fixée, le point mobile B décrit le cercle de diamètre [AC].
L'aire du triangle ABC vaut AC × BH, avec H pied de la hauteur issue de B.
L'aire du rectangle est 2 A(ABC) = AC × BH.

Cette aire est maximale lorsque la hauteur est le rayon [EO].

Le rectangle maximal est le carré AECF, avec E et F milieux des demi-cercles de diamètre [AC].

Figure interactive dans GeoGebraTube : aire maximale d'un rectangle de diagonale constante

Soit ABCD un rectangle de diagonale de longueur fixée, le sommet C est situé sur un cercle de centre A.
Avec le même angle BÂD, un carré AEFG dont la diagonale [AF] a la même longueur que celle du rectangle ABCD.

Il suffit de vérifier que l'aire du rectangle GICD vert est inférieure à celle du rectangle BEFI rose pour conclure.

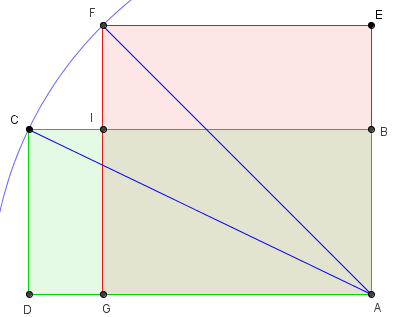
La longueur GI est inférieure à la longueur BI, égale au côté du carré.
La largeur CI est inférieure à la largeur FI car l'angle en F du triangle rectangle CIF est inférieur à 45°.

A(GICD) < A(BEFI) d'où A(GICD) + A(ABIG) < A(BEFI) + A(ABIG),
soit A(ABCD) < A(AEFG).

Figure interactive dans GeoGebraTube : aire d'un rectangle de diagonale constante

Table des matières

Menu optimisation

Optimisation en seconde

1S - TS : Problèmes d'optimisation

Dans d'autres pages du site

Partage d'un triangle en deux polygones de même aire

Aire maximale d'un rectangle dans un triangle rectangle

Distance ou périmètre minimum

Distance minmale dans un triangle avec GeoGebra

    GeoGebraTube : distance minimale dans un triangle rectangle

Google friendly