Descartes et les Mathématiques

Lieux géométriques au collège

Travaux pratiques de mathématiques assistés par ordinateur - recherche de lieux de points mobiles.

Deux figures-clefs proposées dans le « point de vue d'un auteur de manuel » de Terracher aux Journées Nationales de l'APMEP de Grenoble.

Sommaire

1. Lieu du transformé d'un point mobile sur un cercle

2.a. Milieu entre les sommets de deux triangles équilatéraux

2.b. Aires d'un triangle entre deux triangles équilatéraux et du quadrilatère qu'ils forment

3. Le carré mobile

4. Point variable dans un rectangle

1. Lieu du transformé d'un point mobile sur un cercle

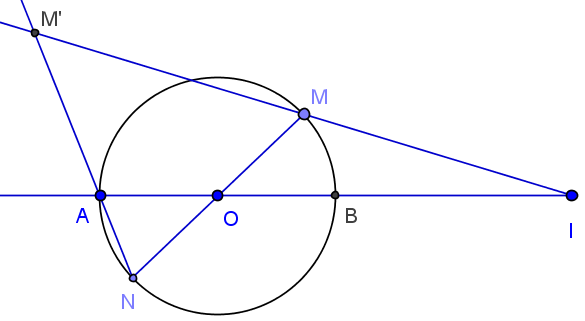
Énoncé du problème

Soit un cercle de centre O et un point I à l'extérieur du cercle, la droite (OI) coupe le cercle en A et B.

Étant donné un point M variable sur le cercle, le rayon (MO) recoupe le cercle en N.

Les droites (IM) et (NA) se coupent en M’.

Quel est le lieu du point M’ ?

Figure interactive dans GeoGebraTube : lieu piloté par un point sur un cercle

Solution : le lieu du transformé est un cercle

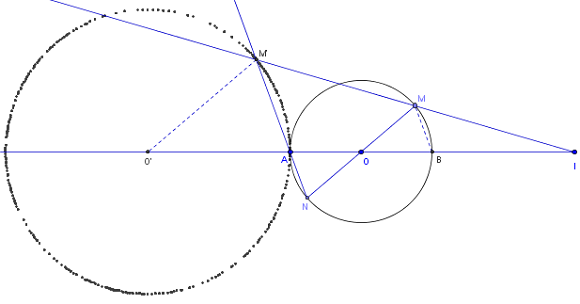
Dessiner le segment [BM]. On fait apparaître une configuration de Thalès. Les cordes [BM] et [AN] étant parallèles, dans le triangle IAM, on a :
IM’/IM = IA/IB ( = k).

En traçant la parallèle à (OM) passant par M’, qui coupe (IA) en O’, la configuration de Thalès dans le triangle IO’M’ permet d'écrire : O’M’/OM = IO’/IO = IM’/IM.
Quel que soit le point M, ce rapport reste égal à k = IA/ IB.
Le point O’ est fixe, avec IO’ = k IO.
Le point M est situé sur le cercle de centre O’ de rayon kr, où r = AB/2.

Autrefois on montrait la réciproque, en remarquant que tout point M’ de ce dernier cercle est image de M, l'un des points d'intersection de la droite (IM’) et du cercle de diamètre [AB].

Dualité

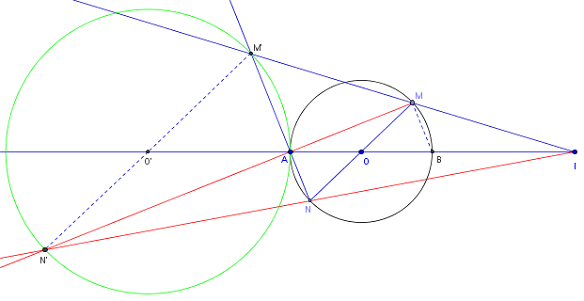
Il est possible de réaliser la même transformation avec le point N.
Les droites (IN) et (MA) se coupent en N’.
Le lieu des points M’ et N’ est le cercle de diamètre M’N’.

Figure interactive dans GeoGebraTube : lieu des transformés de deux points mobiles sur un cercle

Avant la réforme du lycée, il était possible de traiter ce lieu avec l'homothétie de centre I et de rapport IA/IB.

Voir aussi : cordes de cercles tangents et point fixe : angles - rotations

2.a. Milieu entre les sommets de triangles équilatéraux

Classe de troisième ou de seconde ; épreuve externe du CAPES

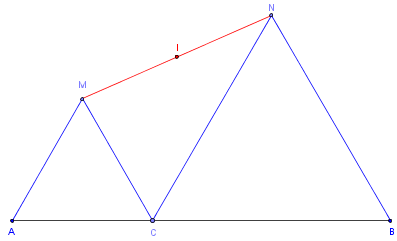
Énoncé

C est un point variable sur un segment [AB].
On trace les deux triangles équilatéraux « directs » ACM et CBN.

Quel est le lieu du point I, milieu de [MN], lorsque le point C est variable sur [AB].

Recherche en géométrie dynamique

Déplacer le point C. Le point I semble appartenir à une droite parallèle à (AB).

Le lieu du milieu est un segment

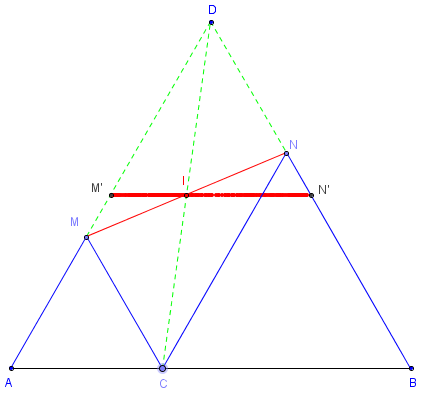
Démonstration

Tracer le triangle équilatéral direct ABD. Le quadrilatère MCND, ayant ses côtés deux à deux parallèles, est un parallélogramme. Le point I milieu de la diagonale [MN] est aussi le milieu de la diagonale [CD]. Le point I est aussi situé sur la droite [M’N’] où M’ et N’ sont les milieux de [AD] et [BD].

Réciproquement, on montre que quel que soit le point I du segment [M’N’], le point C intersection de (DI) et (AB) permet de trouver les deux triangles équilatéraux ACM et CBN correspondants à I.

Conclusion : le lieu du point I est le segment [M’N’].

Figure interactive dans GeoGebraTube : milieu entre les sommets de deux triangles équilatéraux

Voir aussi : cas particulier du triangle de Napoléon

2.b. Thème : optimisation - CAPES Externe de mathématiques 2011

Triangle entre deux triangles équilatéraux

L'exercice : aire maximale d'un triangle entre deux triangles équilatéraux et aire minimale du quadrilatère qu'ils forment

Soit [AB] un segment de longueur 1 et soit C un point de [AB] distinct de A et B.
On construit, du même côté du segment [AB], les triangles équilatéraux ACM et CBN.
1) Existe-t-il une position du point C telle que le triangle CMN ait une aire maximale ?
2) Expliquez pourquoi cette position du point C rend minimale l'aire du quadrilatère ABNM.

La solution proposée par un élève à la question 1) dans un devoir à la maison

Comme je ne trouvais rien malgré le temps qui passait, j'ai cherché « aire d'un triangle » sur WikiPédia et j'ai trouvé trois formules :
  • une qui utilise base fois hauteur mais je ne connais pas la hauteur de CMN, alors je l'ai éliminée ;
  • une autre la formule de Héron, mais il faut connaître les trois côtés et je n'en connais que deux ;
  • donc j'ai utilisé la troisième S = ab sin(C)

Je trouve S = x(1 – x) sin(60°) = x – x²

Le maximum est obtenu au sommet de la parabole pour x = = 0,5 et ce maximum vaut f(0,5) = .

Le travail à exposer devant le jury

1 – Quelles sont les connaissances et les compétences mises en jeu dans l'exercice ?
2 – Analysez la production de l'élève. En particulier
    – que dire de sa démarche ?
    – son raisonnement vous semble-t-il valable ?
    – comment pourriez-vous amener l'élève à justifier au niveau de la classe de seconde la formule de l'aire du triangle qu'il utilise ?
3 – Proposez une correction de la question 2) comme vous l'exposeriez devant une classe de seconde.
4 – Présentez deux ou trois exercices sur le thème « optimisation ».

Conjecture pour l'aire et le périmètre du triangle

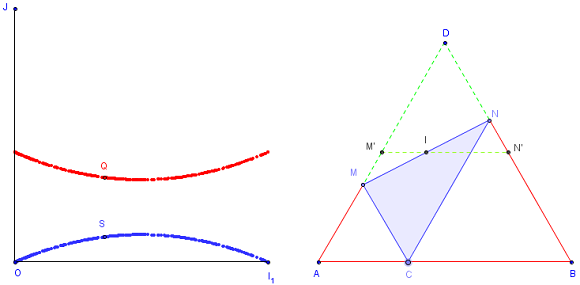
Pour résoudre ce problème d'optimisation :
deux cadres dans l'écran GeoGebra ; le cadre de droite pour la figure géométrique,
le cadre de gauche pour les fonctions permettant la recherche d'extrema.

Dans un repère (O, I₁, J), représenter les points S et Q d'abscisse x et d'ordonnées les aires de CMN et AMNB.
Les traces de S et Q permettent de conjecturer que les extremums se trouvent pour x = , lorsque C, M et N sont les milieux du triangle équilatéral ABD.

Figure interactive dans GeoGebraTube : aires entre deux triangles équilatéraux

Démonstration géométrique

Comme souvent dans ce site, aux calculs analytiques, je préfère une preuve synthétique par la méthode des aires.

À une symétrie près, par rapport à la médiatrice de [AB], choisir le point C sur [AC’] où C’ est le milieu de [AB].

Maximum de l'aire du triangle CMN

Soit C’, M’ et N’ les milieux du triangle équilatéral ABD.
Le triangle C’M’N’ a une aire maximale.

Démonstration

Pour montrer que l'aire du triangle variable CMN est inférieure à l'aire de C’M’N’, comparer l'aire de DMN et celle de DM’N’.

La symétrie de centre I, milieu du parallélogramme MCND, transforme le triangle CMN en DNM, triangles de même aire.
Le point M’, situé sur le côté [DM], a pour symétrique M₁, intersection de (M’N’) et de (CM).
Le triangle IMM’a pour symétrique INM₁, triangles de même aire.

Le triangle DMN a donc même aire que le quadrilatère DM’M₁N. En ajoutant, à cette surface, le triangle équilatéral NM₁N’,
de côté de longueur | – x|, on obtient le triangle DM’N’.

Les triangles C’M’N’ et DM’N’, symétriques par rapport à (M’N’) ont même aire.

L'aire de CMN est égale à l'aire de C’M’N’ diminuée de l'aire du triangle équilatéral NM₁N’. L'aire de ce triangle équilatéral est minimale lorsque N et N’ sont confondus. L'aire du triangle CMN est alors maximale pour x = , C est en C’.

Figure interactive dans GeoGebraTube : triangle maximum entre deux triangles équilatéraux

Minimum de l'aire du quadrilatère AMNB

De la symétrie des triangles IMM’et INM₁, on déduit que l'aire du quadrilatère AMNB est égale à l'aire du polygone AM’M₁NB.
Cette aire est égale à celle du quadrilatère AM’N’B, augmentée de celle du triangle équilatéral NM₁N’.
Cette aire est minimale lorsque le triangle équilatéral est plat, avec C en C’.

2.c. Un troisième triangle équilatéral

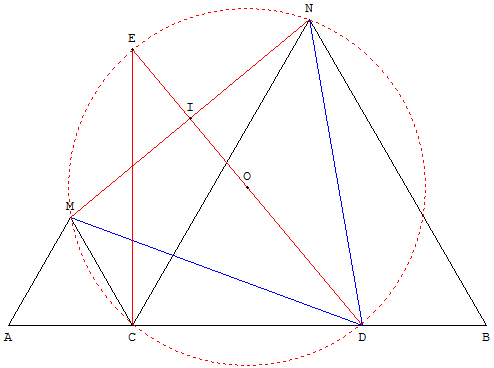
On construit ensuite un troisième triangle équilatéral NMD selon la figure ci-dessus (tels que les triangles ACM, CBM et NMC soient, par exemple, « directs »).

Montrer que le point D appartient à la droite (AB).

Télécharger la figure GéoPlan 3_tri_qui.g2w

Démonstration par les angles inscrits :

Tracer la droite (d) perpendiculaire à (AB) en C.
L'angle MDN étant égal à 60°, les points M, N C et D sont cocycliques. Traçons le cercle (c) en question qui recoupe (d) en E.

Les demi-droites [CM) et [CN) font avec (d) un angle de 30° : les angles inscrits MCE et ECN interceptent les arcs égaux ME et EN ; ME = EN et la médiatrice de [MN] coupe (d) en E.

La médiatrice [ED] de [MN] est un diamètre du cercle passant par D : le triangle ECD est rectangle en C.

Par construction la droite (CE) est perpendiculaire à (AB) ; on en déduit que le point D appartient à la droite (AB).

Autres figures-clefs proposées par Terracher :

    – deux carrés autour de BOA ;

    – aire délimitée par un périmètre de baignade

3. Le carré mobile

Variante du problème de l'équerre contre un mur proposé au lycée.

Classe de troisième

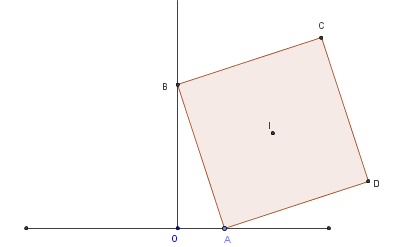
Un carré ABCD, de côté de longueur a, est placée de telle façon que le sommet A est un point variable de l'axe des abscisses (Ox) et le sommet B est sur le demi-axe des ordonnées [Oy).

On déplace le carré en « faisant glisser » les sommets A et B sur les axes.

Montrer que le centre I du carré se déplace sur une droite issue du point O.

Variantes

En classe de quatrième avec l'étude du déplacement du milieu d'une échelle glissant contre un mur vertical, on a montré que la trajectoire du milieu J de [AB] est un quart de cercle de centre O.

Figure interactive dans GeoGebraTube : échelle contre un mur

Le lieu est sur une droite

Indication

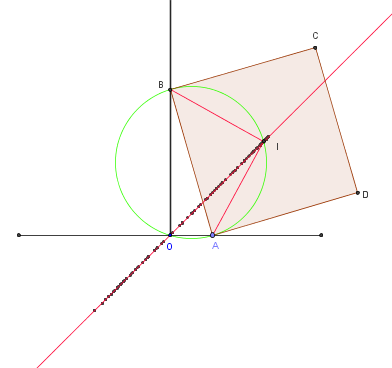
BIA et BOA sont deux triangles rectangles inscrits dans le cercle de diamètre [BA]. Dans ce cercle, les angles inscrits ABI et AOI sont égaux, égaux à 45°.

Le point I se trouve sur la droite fixe passant par O faisant cet angle égal à ABC avec l'axe (Ox).

Le lieu L des points est un segment porté par cette bissectrice des deux axes.

Figure interactive dans GeoGebraTube : carré mobile

Le lieu est une demi-ellipse

Terminale S (L'ellipse est hors programme)

On s'intéresse à l'étude du lieu de certains points du carré lorsque l'on fait glisser les points A et B.

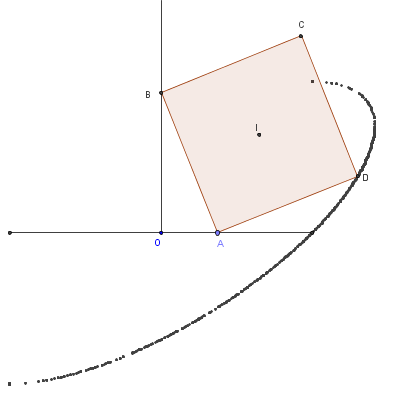
On a montré que pour un point G du carré situé sur le demi-cercle de diamètre [AB], le lieu est un segment porté par une droite passant par O, droite faisant un angle égal à ABG avec l'axe (Ox).

La trajectoire d'un point quelconque G du carré est une demi-ellipse.

Exemple : lieu du sommet D.

Télécharger la figure GéoPlan equerre5.g2w

Étude du lieu du sommet D avec GeoGebra

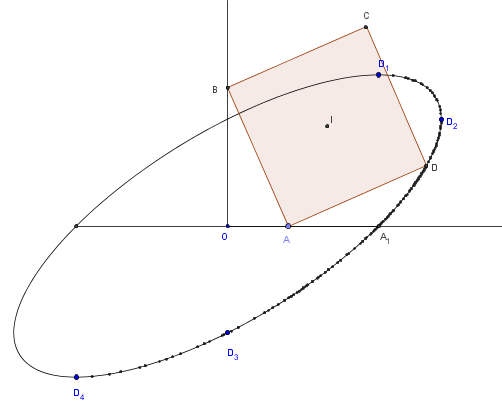
En déplaçant le point A, on peut conjecturer que le point D semble appartenir à une conique.

On trouve alors cinq positions particulières du point D :

A₁(a, 0) ; D₁(a, a) ; D₂(a, a) ; D₃(0, – a) ; D₄(–a, –a).

GeoGebra permet de tracer la conique passant par ces cinq points.
GeoGebra affiche cette demi-ellipse de D₁ à D₄ comme lieu du point D, qui se confond avec la courbe précédente.

4. Point variable dans un rectangle

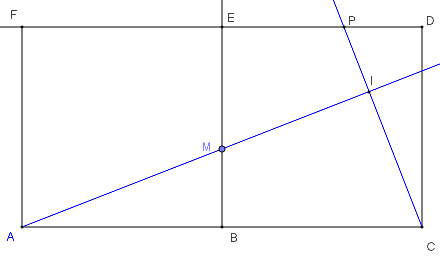
Deux carrés ABEF et BCDE forment un rectangle ACDF de longueur double de la largeur.

Un point M est variable sur la demi-droite [BE).
On reporte la longueur BM sur [DE) de telle sorte que DP = BM.

Déterminer le lieu géométrique du point I,
intersection des droites (AM) et (CP).

Figure interactive dans GeoGebraTube : point variable dans un rectangle

Le lieu est un demi-cercle

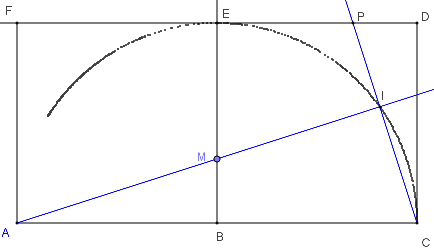
L'angle AIC est droit :
le point I est situé sur le demi-cercle de diamètre [AB].

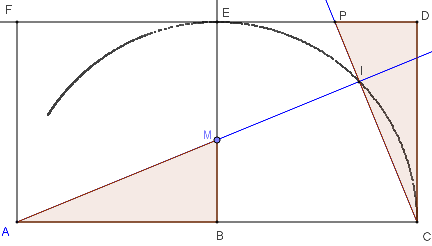
Montrer que les triangles ABM et CDP sont isométriques,
avec leurs côtés deux à deux perpendiculaires.

Autrefois, on montrait que la rotation de centre E et d'angle 90°
transformait ABM en CDP.

Table des matières

Dans d'autres pages du site

Diagonale variable d'un rectangle

Lieux géométriques au lycée

Bissectrice

Lieux des points remarquables dans un triangle

      Cercles d'Apollonius

Arc capable

Lieux faisant intervenir des paraboles

Exercices de-ci, de-là : un cercle comme lieu

Google friendly