Descartes et les Mathématiques
Lieux géométriques du plan avec la géométrie dynamique
Recherche de lieux de points mobiles : milieux, cercles, symétriques…
Lieux géométriques simples
1. Centres des cercles tangents à deux cercles
2. Intersection de deux cercles
3. Lieu du milieu d'un segment
4. Lieu d'un projeté orthogonal
5. Lieu des symétriques d'un point
6. Autre milieu
8. Le carré variable
Problèmes de lieux
Lieux de points remarquables dans le triangle
L'équerre contre un mur ou l'échelle glisse contre un mur
Lieu géométrique avec une rotation et une similitude
Lieu du centre d'un triangle équilatéral inscrit dans un carré
Un lieu géométrique est un ensemble de points satisfaisant certaines conditions, données par un problème de construction (par exemple à partir d'un point mobile sur une courbe) ou par des équations reliant des fonctions de points (notamment des distances).
Latin - English – lieu : locus – plural : lieux : loci
Extrait de l'ancien programme de 1ère S
La problématique des lieux géométriques sera présente dans tous les paragraphes de géométrie. Elle ne fera pas l'objet d'un chapitre indépendant.
Les logiciels de géométrie dynamique seront utilisés pour visualiser certains lieux.
Il s'agit de ne pas s'en tenir à une simple observation, mais de mobiliser les connaissances pour établir mathématiquement diverses caractéristiques géométriques.
On choisira quelques exemples mettant en évidence la diversité des méthodes de recherche : produit scalaire, transformations, géométrie analytique). On veillera à traiter des cas nécessitant de démontrer une double inclusion.
On s'appuiera, le cas échéant, sur le caractère bijectif des transformations ou sur une démarche d'analyse-synthèse.
1. Centres des cercles tangents à deux cercles tangents donnés
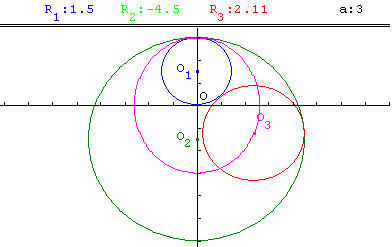
Un cercle variable C3(O3 ; |R3|) est tangent à deux cercles fixes C1(O1 ; |R1|) et C2(O2 ; |R2|), eux même tangents entre eux.
On cherche le lieu L des centres des cercles C3 lorsque R3 varie.
Avec GéoPlan, explorer la situation en faisant varier R1, R2 ou R3 (touches 1, 2 ou 3).
La courbe semble être une conique. Une étude bifocale, avec le calcul de O3O1 + O3O2, permettra dans certains cas de trouver facilement une ellipse.
Par contre, le calcul de la différence O3O1 - O3O2, pour l'étude bifocale de l'hyperbole, est plus délicat et dépasse les compétences d'un élève de 1ère S !
Paramètres modifiables : O1 centre du premier cercle ; des mesures algébriques R1, R2 et R3 correspondant aux rayons des trois cercles.
O est le milieu du segment [O1O2]. a est la moitié de la différence entre R1 et R2.
Figure ci-contre : C1 et C3 sont à l'intérieur de C2 ; L est une ellipse.
L est une branche d'hyperbole ; C1, C2 et C3 sont tangents extérieurement.
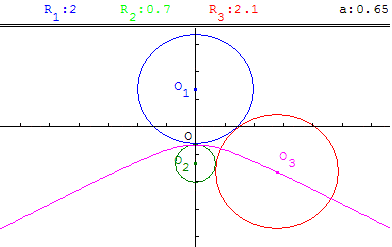
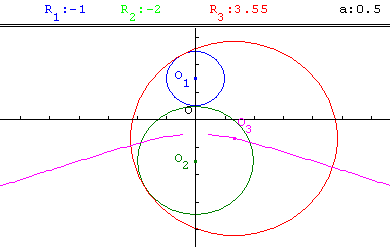
L est une partie d'une branche d'hyperbole “il manque un arc autour du sommet” ; C1 et C2 sont à l'intérieur de C3.
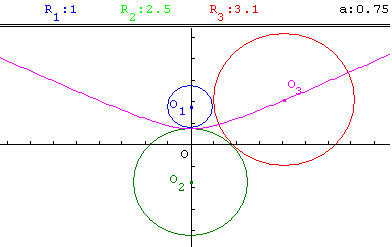
L est une branche d'hyperbole.
Télécharger la figure GéoPlan certang4.g2w
Cercle tangent à deux cercles, passant par un point : voir problème de contact PCC
Cas limite
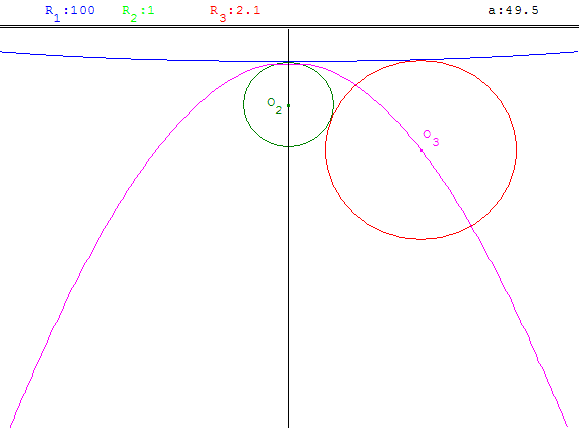
On n'a pas de parabole, mais lorsque R1 est grand par rapport à R2 on trouve la curieuse branche d'hyperbole suivante !
2. Intersection de deux cercles
Énoncé de l'exercice
Soit (d) une droite fixée du plan et un point A n'appartenant pas à (d).
Pour chaque point M de la droite (d) on considère les cercles (c) de centre M passant par A et (c’) de centre A passant par M.
Quels sont les lieux géométriques (L1) et (L2) des points M1 et M2, intersection des deux cercles ?
Méthode à mettre en œuvre
On considére les transformations T et T’ suivantes :
é tout point M de(d) on fait correspondre par T le point M1 intersection des cercles (c) et (c’) tel que la mesure de l'angle
orienté (
; 
) soit positif ;
et par T’ le deuxième point M2 d'intersection de ces deux cercles tel que la mesure de l'angle orienté
( ; 
) soit négatif.
AMM1 et AMM2 sont des triangles équilatéraux, T et T’ sont les rotations de centre A et d'angles
et - .
Les droites (L1) et (L2) sont les images par T et T’ de la droite (d).
Leur point d'intersection est le symétrique
de A par rapport à (d).
Note technique GéoPlan :
Points fixes : A ; B et C définissant la droite (d) = (BC),
point variable : M sur la droite (BC).
L'instruction : M point libre sur la droite (BC) ne permet pas de tracer les lieux L1 et L2 à la demande.
Pour visualiser ces lieux il faut faire varier M sur un segment [B1C1] de la droite (d) = (BC).
Nous avons donc calculé l'équation de la droite (d) et les coordonnées des deux points B1 et C1
de (d) d'abscisses mi et ma suffisamment grandes en valeurs absolues.
2.b. Deuxième point d'intersection de deux cercles
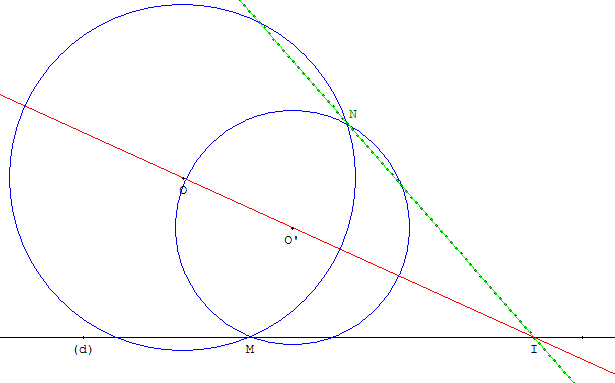
La droite (d) et les points O et O’ sont fixes.
À tout point M de (d) on associe le point N, deuxième intersection des cercles (c) et (c’) de centres O et O’ passant par M.
Quel est le lieu du point N lorsque M décrit la droite (d) ?
Solution
Les points M et N sont symétriques par rapport à la droite (OO’) axe de symétrie des deux cercles.
Le lieu (l) est la droite symétrique de (d) par rapport à (OO’).
3. Lieu du milieu d'un segment
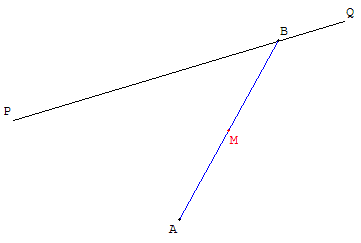
Deux exercices à réaliser …avec GéoPlan, dès la classe de quatrième.
Extrémité mobile sur une droite
Construire un point A fixe et un point B mobile sur une droite (PQ).
Quel est le lieu géométrique du point M ?
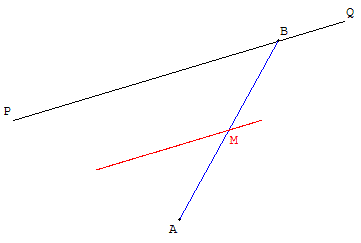
Tracer le milieu M de [AB].
Faire apparaître la figure décrite par le point M lorsque B se déplace sur (PQ).
Démontrer le résultat.
télécharger la figure GéoPlan mil_pt_sur_droite.g2w
Lieu du milieu d'un segment d'extrémité mobile sur un cercle
Construire le cercle (c) de centre O, passant par un point A fixe et placer un point B mobile sur ce cercle.
Tracer le milieu M de [AB].
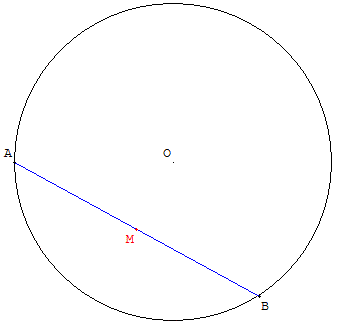
Faire apparaître la figure décrite par le point M lorsque B se déplace sur le cercle.
Quel est le lieu géométrique du point M ?
Démontrer que le lieu du milieu est un dercle
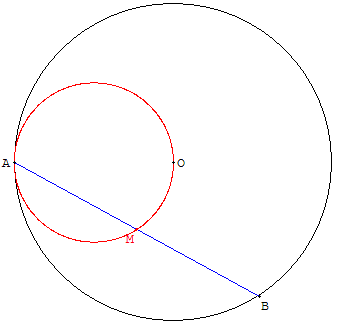
Pour cela, tracer les segments [OA], [OB] et [OM]. Le triangle OAB est isocèle et [OM] est une hauteur. Le triangle rectangle AOM est inscrit dans le cercle de diamètre [OA], lieu du point M.
Autres démonstrations
Tracer le point C diamétralement opposé au point A, le triangle rectangle ACB a pour médiatrice (OM) et on retrouve le triangle rectangle moitié AOM inscrit dans le cercle de diamètre [OA].
Transformation
L'homothétie de centre A et de rapport 
transforme B en C, le cercle (c) a pour image le lieu de M : le cercle de diamètre [OA].
Segment de longueur fixe
A, point libre (pilotable à la souris), varie sur un cercle de centre O et de rayon b.
Le segment [AB] est de longueur fixe a.
M est le milieu de [AB].
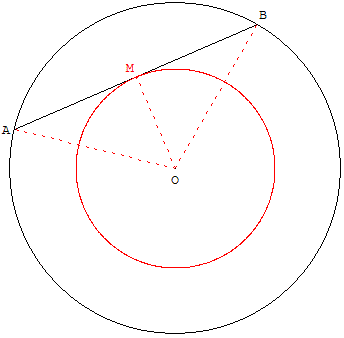
Étudier le triangle OMB lorsque a = 8 cm et b = 5 cm.
Quel est le lieu du point M lorsque le point A se déplace sur le cercle ?
Montrer que la droite (AB) est tangente au cercle fixe de centre O, passant par M.
Extrémités mobiles sur un cercle et une droite
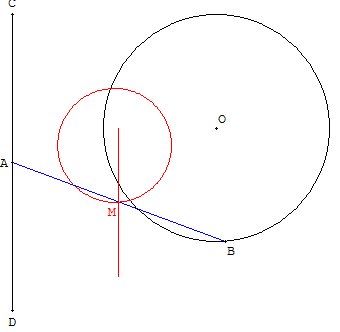
Le point A varie sur un segment [CD].
Le point B varie sur un cercle de centre O.
M est le milieu de [AB].
Étudier le lieu du point M quand A varie (B fixe) ou quand B varie (A fixe)
Extremiés sur les côtés d'un angle droit,
voir : l'échelle contre un mur
4. Lieu d'un projeté orthogonal
Cet exercice permet de proposer deux niveaux d'exploration :
• Analyse des hypothèses de construction pour conjecturer un résultat.
• Mise à l'épreuve de cette conjecture avec la recherche d'une réciproque.
Cette activité permet, de par la forme de son énoncé, de se familiariser avec les fonctionnalités de GéoPlan.
Soit un point P, un cercle (c) de centre O et un point M variable sur le cercle. Soit N le projeté orthogonal du centre O sur la droite (PM).
Quel est le lieu géométrique décrit par le point N, lorsque M décrit le cercle (c) ?
Projeté P à l'intérieur du cercle (c)
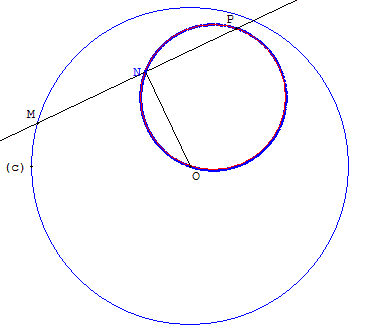
Remarque : O est un point du lieu, le lieu n'est pas vide.
L'angle ONP étant droit, on peut conjecturer que le lieu de N est inclus dans le cercle de diamètre [OP].
Remarque : le point N, milieu de la corde formée par le cercle et la droite (PN), est à l'intérieur du cercle (c).
Cas particulier : si P est sur le cercle, N est le milieu de [MP] et on retrouve le lieu du milieu d'un segment.
Projeté P à l'extérieur du cercle (c)
Réciproque
Si N est un point du cercle de diamètre [OP] et est à l'intérieur du cercle (c), alors la droite (NP), perpendiculaire à (ON) coupe le cercle (c) en un point M (et un point M’ si ce n'est pas une tangente). N, projeté orthogonal du centre O sur cette droite (NP) = (PM), est un point du lieu.
Conclusion
Si P est à l'intérieur du cercle (c), ou est situé sur ce cercle, le lieu est le cercle de diamètre [OP].
Si P est à l'extérieur du cercle (c), le lieu est l'arc du cercle diamètre [OP] situé à l'intérieur de (c), dont les extrémités A et B sont les points d'intersection des deux cercles (inclus dans le lieu).
5. Lieu des symétriques d'un point
A et B sont deux points fixes, la droite (d) est une droite variable passant par le point A.
B’ est l'image de B dans la symétrie par rapport à D.
Quel est le lieu du point B’ lorsque la droite (d) varie ?
6. Lieu d'un autre milieu
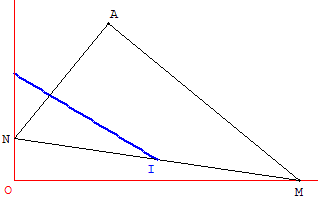
A est un point à l'intérieur du secteur xOy.
M point variable sur (Ox).
Soit N le point de (Oy) tel que MÂN soit droit.
I est le milieu de [MN].
Quel est l'ensemble des points I ?
Le mode trace permet de conjecturer que l'ensemble cherché est situé sur la médiatrice de [OA].
7. Demi-paraboles
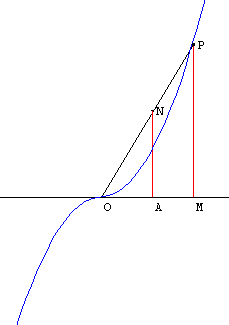
On place deux points O et A tels que OA = 1. Soit M un point variable sur la droite (OA).
Sur la demi-droite perpendiculaire en A à (OA) située dans P1, un des demi-plans de frontière (OA), on trace le point N tel que AN = OM.
La perpendiculaire à (OA) en M rencontre la droite (ON) au point P.
Quel est l'ensemble des points P ?
Le mode trace permet de conjecturer que l'ensemble cherché est constitué de deux demi-paraboles.
Voir : parabole
Épreuve pratique en TS
2007 : Tangente à une parabole
2008 : Points équidistants d'une droite et d'un point
2009 : Propriétés de la parabole
8. Le carré variable
8.a. Lieu du sommet opposé à M, si le côté [AM] varie
Classe de 2nde
Soit une droite (d) et un point fixe A à l'extérieur de (d).
Un point M est variable sur la droite (d).
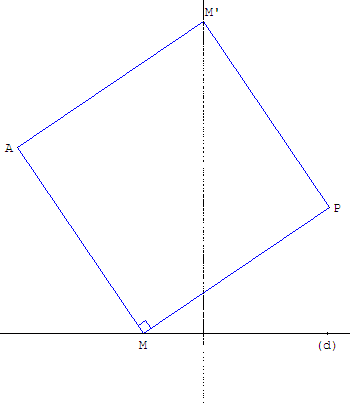
a. Placer les points M’ et P tels que MPM’A soit un carré direct.
On dilate le carré en « faisant glisser » M sur la droite (d).
Quel est le lieu géométrique du point M’, lorsque M se déplace sur (d).
Le mode trace permet de conjecturer que l'ensemble cherché est une droite perpendiculaire à (d).
Indication
Une rotation de centre A.
Variante : le point M se déplace sur un cercle.
8.b. Lieu du sommet consécutif de M, si le côté [AM] varie
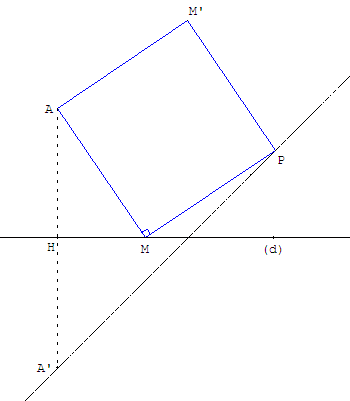
8.c. Lieu des sommets, si la diagonale [AM] varie
Terminale S
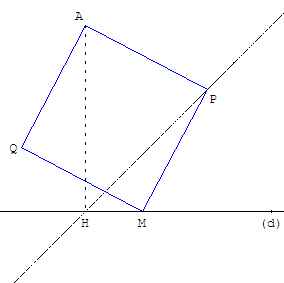
Étudier le lieu du point P à l'aide d'une similitude de centre A.
Placer les points P et Q tels que MPAQ soit un carré direct.
On dilate le carré en « faisant glisser » M sur la droite (d).
À l'aide de similitudes de centre A, dire quels sont les lieux géométriques des points P et Q lorsque M se déplace sur (d).
Voir aussi :
– le carré mobile
9. Quartique de Jules Verne
En 1863, Jules Verne avait anticipé les olympiades de mathématiques et avait proposé le problème suivant dans Paris au XXe siècle, roman non publié à l'époque, mais édité plus d'un siècle plus tard, par Hachette en 1994 et France Loisirs en 1995.
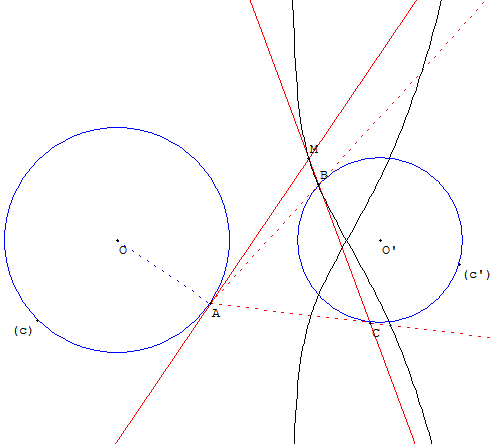
Soit (c) et (c’) deux cercles de centres O et O’.
D'un point A de (c), on mène deux tangentes à (c’). On joint les de contact B et C de ces tangentes.
On mène la tangente en A au cercle (c).
On demande le lieu du point M d'intersection de cette tangente avec la corde des contacts du cercle (c’).
Le lieu est une quartique : courbe algébrique de degré 4
openclassrooms forum probleme jules Verne et quartique
Table des matières
Google friendly
Dans d'autres pages du site
Exercices de-ci, de-là : un cercle comme lieu
Exemples de lieux du plan
La médiatrice d'un segment est le lieu des points équidistants des extrémités de ce segment.
La bissectrice d'un angle est lieu des points équidistants des côtés de cet angle.
Un arc capable est le lieu des points d'où l'on « voit » un segment selon un angle donné.
Les sections coniques pourraient être définies comme des lieux :
Le cercle est le lieu de points pour lesquels la distance au centre est égale au rayon.
L'ellipse est le lieu des points pour lesquels la somme des distances aux foyers est une valeur donnée.
L'hyperbole est le lieu de points dont la différence des distances aux foyers est une valeur donnée.
La parabole est le lieu de points pour lesquels les distances du foyer et à la droite directrice sont égales.
Tangentes de la parabole et lieu géométrique
Points équidistants d'une droite et d'un point
Constructions mécaniques de courbe : conchoïde de droite
Téléchargement des anciennes versions de 2008
Télécharger lieux_geometriques.doc : ce document au format « .doc »
Télécharger lieux_geometriques.pdf : ce document au format « .pdf »
Google considère l'URL comme une erreur de type "soft 404.
|
|
Page no 40, réalisée le 28/5/2003 |