Descartes et les Mathématiques

Épreuve pratique de terminale S

Sujets 2008 de géométrie plane

Banque de sujets de géométrie planeen TS proposés par ÉduSCOL en 2008.

Sommaire

Sujets corrigés

6. Tangentes à deux courbes

14. Distance d'un point à une courbe

20. Étude d'un lieu de points

21. Recherche d'un lieu géométrique

26. Positions relatives dans une configuration

39. Cercles et similitudes

45. Points équidistants d'une droite et d'un point

90. Étude de lieux géométriques

93. Triangle inscrit dans une courbe donnée

Sujets non retenus

15. Tangentes communes à deux courbes
27. Cercles et paraboles
46. Optimisation d'une aire
47. Étude d'un lieu géométrique
50, 52. Déformation d'une figure géométrique
59. Suite définie géométriquement
70. Étude d'un problème de géométrie dans le plan complexe
72, 78. Recherche d'un point fixe
84. Extremum
95. Étude d'un lieu géométrique

Mobile friendly

Corrigé des sujets retenus à l'épreuve de 2008

Ci-dessous la liste des « descriptions » et « fiches élèves » retenues en 2008 en géométrie plane.
Les sujets de géométrie dans l'espace se trouvent dans la page : l'épreuve pratique avec GéoSpace.

6. Tangentes à deux courbes

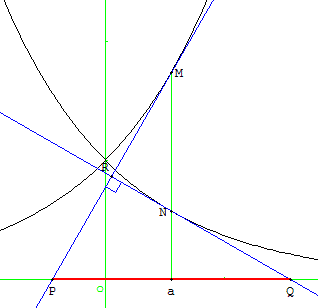
Situation
Dans un repère orthonormal du plan, on considère les courbes C₁ et C₂ représentatives de deux fonctions.
On désigne respectivement par M et N des points de C₁ et C₂ et par (T₁) et (T₂) les tangentes à C₁ et C₂ en M et N.
Il s'agit d'étudier des propriétés géométriques de ces tangentes.

Énoncé

Soit C₁ et C₂ les courbes d'équations respectives y = exp(x) et y = exp(−x) dans un repère
(O, , ) orthonormal du plan.
Soit a un nombre réel quelconque. On désigne respectivement par M et N les points de C₁ et C₂ d'abscisse a et par (T₁) et (T₂) les tangentes à C₁ et C₂ en M et N.
Les droites (T₁) et (T₂) coupent respectivement l'axe des abscisses en P et Q.

1. Avec un logiciel de géométrie dynamique (ou une calculatrice graphique) construire les courbes C₁ et C₂ et les droites (T₁) et (T₂).
Que peut-on remarquer pour les droites (T₁) et (T₂) ?
Appeler le professeur pour lui montrer le graphique créé et lui indiquer la conjecture faite au sujet de (T₁) et de (T₂).

2. À l'aide du logiciel, émettre une conjecture à propos de la longueur du segment [PQ].

3. Démontrer la conjecture émise à la question 2.

Indications

Les droites (T₁) et (T₂) sont perpendiculaires (produit des coefficients directeurs des droites ègal à −1). PQ = 2.

Télécharger la figure GéoPlan tangente_exponentielle.g2w

Compétences évaluées
Compétences TICE
  • Représenter graphiquement des courbes et leurs tangentes en un point donné ;
  • Émettre et tester des conjectures.

Compétences mathématiques
  • Équation de la tangente en un point d'une courbe ;
  • Techniques de géométrie analytique.

14. Distance d'un point à une courbe

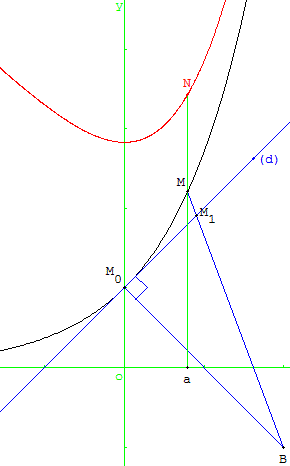
Situation
On considère dans le plan P, muni d'un repère orthonormal, la courbe C représentative d'une fonction. Il s'agit de déterminer la distance d'un point B donné à la courbe C.

Énoncé

Dans le plan P rapporté à un repère orthonormal (O ; , ) la courbe C est la courbe représentative de la fonction exponentielle et le point B a pour coordonnées (2 ; −1).
On admet que la distance BM admet un minimum quand M décrit C. Ce minimum est appelé distance du point B à la courbe C.
Le but de l'exercice est de trouver la distance du point B à la courbe C.

1. Réaliser à l'aide d'un logiciel une figure dynamique correspondant à cette situation.
Appeler l'examinateur pour une vérification de la figure réalisée.

(a) M est un point quelconque de la courbe C. Faire une conjecture sur la position du point M pour laquelle la distance BM semble minimale.
On appelle ce point M₀.
(b) Tracer la droite d perpendiculaire en M₀ à la droite (BM₀).
Quelle semble être la position particulière de la droite d ?
Appeler l'examinateur pour lui présenter les conjectures émises et lui indiquer la ou les méthodes de contrôle prévues à la question (c).
(c) Utiliser le logiciel pour contrôler les conjectures et, éventuellement, les rectifier.

2. On se propose de déterminer la valeur exacte de la distance du point B à la courbe C.
Appeler l'examinateur pour lui présenter les contrôles faits et lui proposer une méthode permettant à la fois de déterminer le point M₀ et la distance du point B à la courbe C.

(a) Déterminer, par le calcul, la position du point M₀.
(b) Quelle est la valeur exacte de la distance du point B à la courbe C ?

3. Vérifier, par le calcul, la conjecture formulée au 1.(b).

Indications

1. Le point M₀ a pour coordonnées (0, 1). Le point B se projette en M₀ sur la tangente d à C en M₀. d a pour équation y = x + 1.

2. On peut représenter le point N dont l'ordonnée est la distance BM et faire le tracé du lieu du point N. Vérifier que ce graphe admet un minimum.

Démonstration géométrique basée sur la convexité de la courbe exponentielle

Pour un point M sur C, le segment [BM] coupe la tangente d en M₁.
BM = BM₁ + M₁M ≥ BM₁ ≥ BM₀ et BM₀ est bien la distance minimale.

3. Démonstration algébrique

Il est enfin possible de calculer le carré de la longueur BM pour éviter des racines carrées.
On a h(x) = BM² = (x − 2)² + (exp(x) + 1)².

La dérivée h’(x) = e^2x + e^x + x - 2 est une somme de fonctions croissantes, donc une fonction croissante qui s'annule pour x = 0.
La fonction h admet donc son minimum pour x₀ = 0, correspondant au point M₀(0, 1), soit BM₀² = 8 et BM₀ = 2.

Télécharger la figure GéoPlan distance_point_courbe.g2w

Même exercice en 2009 à partir du point O.

Compétences évaluées
Compétences TICE
  • Utiliser un logiciel de géométrie dynamique ;
  • Visualiser une propriété à partir des fonctions du logiciel.

Compétences mathématiques
  • Connaître les fonctions usuelles ;
  • Déterminer le minimum d'une fonction.

20. Étude d'un lieu de points

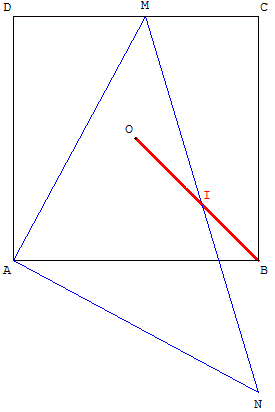
Situation
Détermination d'un lieu de points dans le plan orienté en utilisant des similitudes.

Énoncé

On considère le carré direct ABCD du plan orienté tel que (, ) = . On appelle O le centre du carré. Un point M décrit le segment [DC]. La perpendiculaire à la droite (AM) passant par A coupe (BC) en N. On appelle I le milieu de [MN].

On se propose de déterminer le lieu des points I lorsque M décrit le segment [DC].

1. Réaliser la figure avec un logiciel de géométrie dynamique.
2. Mettre en évidence, avec le logiciel, la nature du triangle AMN.
3. Faire afficher le lieu des points I, lorsque M décrit le segment [DC].

Partie démonstration
4. Démontrer que le triangle AMN est rectangle isocèle (on pourra utiliser une rotation de centre A).
5.    En déduire la nature du triangle AIM ; établir que le point I est l'image de M par une similitude S de centre A dont on précisera l'angle et le rapport.
6. Déterminer S(D) et S(C) puis conclure sur le lieu de points cherché.

Indications

Le point I se déduit de M par une similitude de rapport et d'angle = − .
On a : S(D) = O et S(C) = B. L'image de [DC] est le segment [OB].

Télécharger la figure GéoPlan lieu_similitude.g2w

Compétences évaluées
Compétences TICE
  • Construire une figure à l'aide d'un logiciel de géométrie dynamique ;
  • Tester les conjectures émises ;
  • Visualiser un lieu de points.

Compétences mathématiques (spécialité)
  • Reconnaître et utiliser une rotation et une similitude.

21. Recherche d'un lieu géométrique

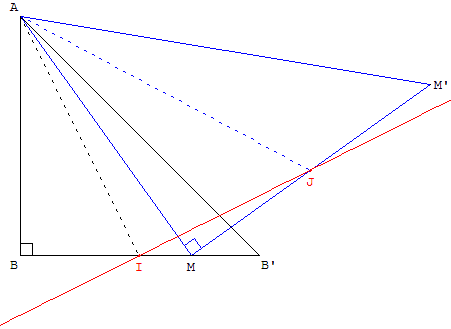
Situation
Dans le plan orienté, on considère un triangle rectangle isocèle. On considère divers points définis à partir d'un point variable sur un côté. L'objectif est de visualiser puis d'établir la nature du lieu de certains de ces points.

Énoncé

Dans le plan orienté, on considère un triangle rectangle isocèle ABB’ tel que : (BB’, BA) = . Soit M un point variable de la droite (BB’) et M’ l'image de A dans la rotation de centre M et d'angle − .
On note I le milieu de [BB’] et J le milieu de [MM’].
On cherche à déterminer le lieu du point J lorsque M décrit la droite (BB’).

1 (a) Réaliser une figure à l'aide d'un logiciel de géométrie dynamique.
   (b) Visualiser le lieu du point J quand M décrit la droite (BB’). Quelle conjecture peut-on émettre ?
   (c) Que peut-on conjecturer à propos des triangles ABI et AMJ ?

2. Soit S la similitude directe de centre A qui transforme B en I.
 (a) Déterminer l'image du point M par la similitude S.
 (b) En déduire le lieu du point J quand M décrit la droite (BB’).

Indications

Les triangles ABI et AMJ sont semblables.
La similitude S transforme donc M en J.
Donc, le lieu de J est l'image de la droite (BB’) par la similitude S : c'est une droite qui passe par I et par I’, l'image de B’ par cette similitude.
La similitude S est de rapport et d'angle atan().

Télécharger la figure GéoPlan lieu_similitude2.g2w

Compétences évaluées
Compétences TICE
  • Construction d'une figure à l'aide d'un logiciel de géométrie dynamique ;
  •  visualisation d'un lieu.

Compétences mathématiques (spécialité)
Reconnaître et utiliser :
  • des triangles semblables ;
  • des angles orientés ;
  • des similitudes directes.

26. Positions relatives dans une configuration

Situation
L'objet du problème est d'étudier, dans une configuration variable du plan, les longueurs et les positions relatives de deux segments.

Énoncé

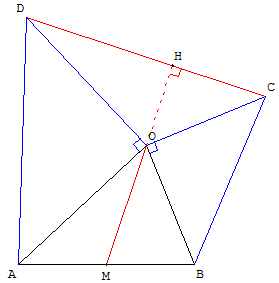
Dans le plan orienté, on définit le triangle direct BOA et on note M le milieu du segment [AB]. On construit les triangles AOD et OBC directs, rectangles et isocèles en O.
L'objet du problème est d’étudier les longueurs et les positions relatives des segments [OM] et [DC].

1. Construire la figure décrite précédemment à l'aide d'un logiciel de géométrie dynamique.

2. En modifiant le triangle OAB, émettre une conjecture concernant les longueurs OM et DC et une autre au sujet des positions relatives des droites (OM) et (DC).

3. Proposer une démonstration des conjectures faites.

Télécharger la figure GéoPlan tr_boa_26.g2w

Démonstration

Il semble que DC = 2OM et que DC et OM sont perpendiculaires.

Utilisation des complexes : dans un repère d'origine O, les affixes des points sont notées par les minuscules correspondantes.
a pour affixe z = (a + b)/2 et pour affixe c − d = i (a + b) donc (c−d)/z = 2i. Ce qui permet de conclure.

Voir une autre démonstration, avec une rotation, dans les problèmes du BOA : la médiane de l'un est la hauteur de l'autre

Compétences évaluées
Compétences TICE
  • Construire une figure à l'aide d'un logiciel ;
  • Émettre des conjectures.

Compétences mathématiques
  • Utiliser des notions de géométrie élémentaire dans le plan.

39. Cercles et similitudes

Situation
Un triangle équilatéral étant donné, on considère une similitude définie par son centre et l'image d'un point particulier.
On recherche l'image d'un cercle, puis le lieu du point d'intersection de deux droites.

Énoncé

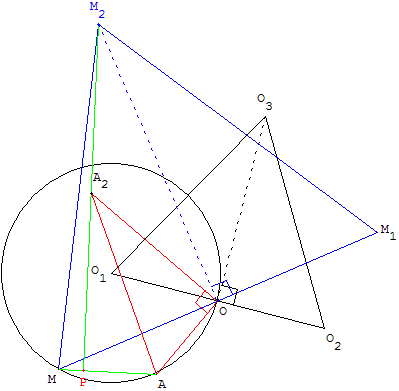
On considère un triangle équilatéral direct O₁O₂O₃, le milieu O du segment [O₁O₂] et le cercle (C) de centre O₁ passant par O. On note A un point du cercle C distinct du point O.
Pour tout point M du cercle (C), on note M₁ le point symétrique de M par rapport à O puis M₂ le point tel que le triangle MM₁M₂ soit équilatéral direct.

Partie expérimentale
1.  À l'aide d'un logiciel de géométrie dynamique, construire le triangle O₁O₂O₃, placer le point O et tracer le cercle (C).
2.  Le point A étant construit sur le cercle (C), construire le point A₂ associé au point A par le procédé indiqué dans le préambule.
3. Placer un autre point, noté M, sur le cercle (C) et construire le point M₂ associé à ce point.
Visualiser la courbe (ou lieu) que semble d’écrire le point M₂ lorsque le point M décrit le cercle (C) et émettre une conjecture à ce propos.
4. Lorsque les points M et A sont distincts, les droites (AM) et (A₂M₂) se coupent en un point P. Placer le point P sur la figure. Émettre une conjecture concernant le lieu décrit par le point P lorsque le point M décrit le cercle C privé du point A.

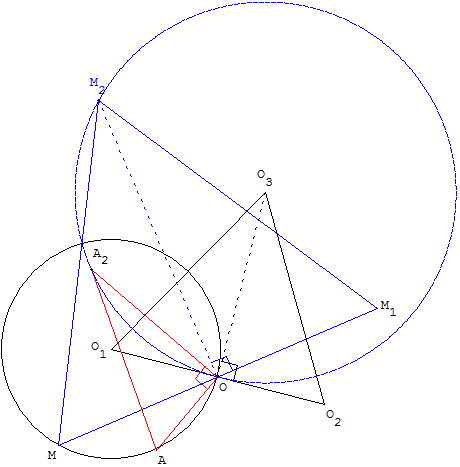
Télécharger la figure GéoPlan cercle_similitude.g2w

Démonstration

1. Montrer qu'il existe une similitude directe de centre O par laquelle le point M du cercle (C) a pour image le point M₂. Préciser l'angle et le rapport de cette similitude.
2. Déterminer le lieu du point M₂ lorsque le point M décrit le cercle C.
3. Préciser le lieu du point P lorsque le point M décrit le cercle C privé du point A.

Indications

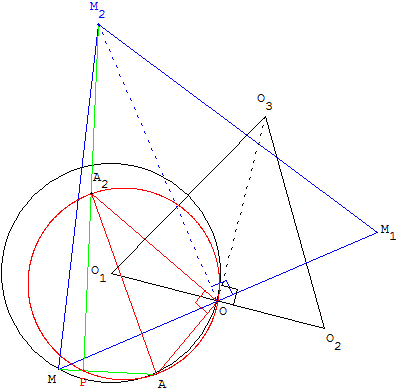
1. La similitude s de centre O, d'angle , de rapport transforme M en M₂.
2. Le lieu du point M₂ est le cercle (C₂) de centre O₃ passant par O.
Remarque : on retrouve ici la configuration classique d'alignement avec un point et son transformé dans une similitude

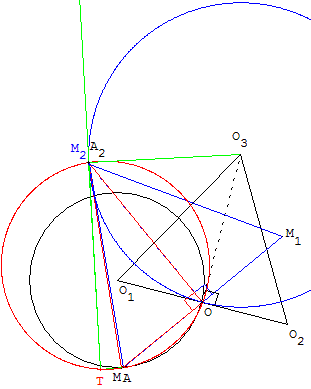
3. La similitude s transforme M en M₂ et A en A₂. La droite (AM) a pour image par s la droite (A₂M₂). Leur angle est , angle de la similitude. L'angle APA₂ est droit. Le point M est situé sur le cercle (C₃) de diamètre [AA₂].

Étant donné un point P du cercle de diamètre [AA₂], (AP) recoupe le cercle C en M, si la droite (PA₂) recoupe le cercle (C₂) en un point M₂, celui est associé au point M. C'est le cas pour tout point P du cercle (C₃), sauf pour le point T où la droite (TA₂) est tangente au cercle (C₂) en A₂. Le point M est alors en A.
Le lieu est donc (C₃) − {T}, avec T point d'intersection de (C₃) avec la perpendiculaire en A₂ à
(A₂O₃).

Remarque hors programme : les cercles (C₂) et (C₃), ainsi que (C₂) et (C), sont orthogonaux.

Compétences évaluées
Compétences TICE
  • Construire une figure avec un logiciel de géométrie ;
  • Visualiser un lieu de points.

Compétences mathématiques (spécialité)
  • Connaître les propriétés des similitudes ;
  • Reconnaître et utiliser une configuration usuelle.

45. Points équidistants d'une droite et d'un point

Situation
On considère dans le plan (P) une droite et un point non situé sur cette droite. Il s'agit de déterminer le lieu géométrique des points du plan équidistants de la droite et du point.
Dans un premier temps, on visualise le lieu à l'aide d'un logiciel de géométrie dynamique. Dans un deuxième temps, on détermine son équation.

Énoncé

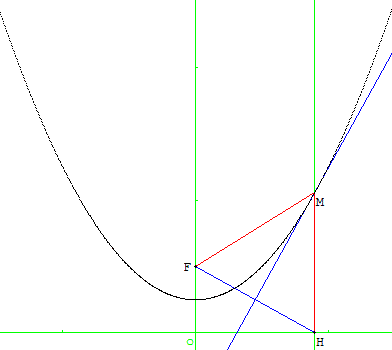
On considère dans le plan (P) une droite D et un point F non situé sur cette droite. Il s'agit de déterminer l'ensemble G, lieu géométrique des points du plan équidistants de D et de F.

Partie expérimentale
1. À l'aide d'un logiciel de géométrie dynamique, construire la droite D et le point F.
Construire également un point H sur la droite D et la droite T perpendiculaire à D en H.

2. Construire un point M de T équidistant de F et de H.
Construire le lieu géométrique du point M lorsque le point H décrit la droite D. Quelle conjecture peut-on faire sur la nature de G ?

3. On considère un repère orthonormal direct (O, , ) tel que D est la droite (O, ) et le point F est sur la droite (O, )
Pour un point M (x, y) quelconque du plan, on considère le point H, projeté orthogonal de M sur la droite D.
(a) Calculer MF² et MH² en fonction de x et y et en déduire une condition liant x et y pour que le point M soit équidistant de F et de D.
(b) Donner alors une équation de G et conclure.

Indication

M est situé à l'intersection de T et de la médiatrice de [HF].
G est l'ensemble des points M tels que MF = MH.
Le point F est appelé le foyer de la parabole et la droite D la directrice.
Dans le repère (O, , ), le point F a pour coordonnées (0, p) et la parabole a pour équation y = k x² + = x² + .

Technique GéoPlan : pour tracer le lieu géométrique, H ne peut pas être un point libre sur la droite D, mais doit être un point libre sur un segment.
Donc placer deux points H₁(0, −3) et H₂(0, 3) et créer le point H comme point libre dans le segment [H₁H₂].

Télécharger la figure GéoPlan pa_foyer.g2w

Voir : parabole

Tangente à une parabole : épreuve pratique 2007

Cercles et paraboles : épreuve pratique 2008

Propriétés de la parabole : épreuve pratique 2009

Compétences évaluées
Compétences TICE
  • Réaliser des constructions avec un logiciel de géométrie dynamique ;
  • Émettre des conjectures.

Compétences mathématiques
  • Équation de la médiatrice d'un segment ;
  • Équation cartésienne d'une parabole.

90. Étude de lieux géométriques

Situation
Étude du lieu de deux points définis comme des projetés orthogonaux d'un point M décrivant une figure simple.

Énoncé

Dans le plan muni d'un repère orthonormal direct (O, , ) on considère les points
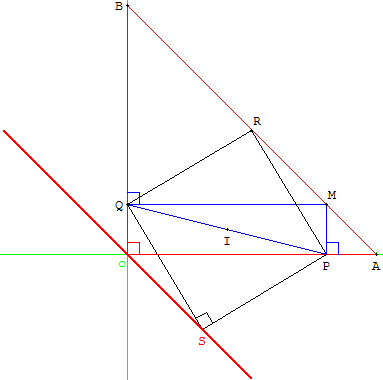
A(1 ; 0) et B(0 ; 1). À tout point M du segment [AB], on associe les points P et Q, projetés orthogonaux respectifs de M sur les droites (OA) et (OB), et les points R et S, sommets du carré PRQS de diagonale [PQ] tels que (, ) = . On note aussi I le milieu du segment [PQ].

Le but de l'exercice est d’étudier les lieux des points R et S lorsque M décrit le segment [AB].

1. (a) Réaliser une figure à l'aide d'un logiciel de géométrie dynamique.
    (b) Visualiser les lieux des points R et S quand M décrit le segment [AB], puis émettre une conjecture sur la nature de ces lieux.
    (c) Déterminer de manière expérimentale une équation du lieu du point S.

2. Dans cette question, on se propose d’étudier ces conjectures en se plaçant dans le plan complexe.

On appelle x l'abscisse du point M, avec x ∈ [0 ; 1].
    (a) Montrer que l'affixe de M est : x + i(1 − x).
    (b) Déterminer l'affixe de R ou celle de S. Justifier l'une des conjectures émises à la question 1.

Télécharger la figure GéoPlan lieu_projete.g2w

Production demandée
  • Visualisation à l'écran de la figure ;
  • Démarches et réponses argumentées pour les questions 2.(a) et 2.(b).

Compétences évaluées
Compétences TICE
  • Construction d'une figure avec un logiciel de géométrie dynamique ;
  • Visualisation d'un lieu.

Compétences mathématiques
  • Calculs avec les nombres complexes ;
  • Justification d'un alignement.

93. Triangle inscrit dans une courbe donnée

Situation
Il s'agit d'étudier quelques propriétés des triangles dont les trois sommets appartiennent à une courbe donnée.

Énoncé

Le plan est rapporté a un repère orthonormal (O ; , ).
On appelle G la courbe d’équation y = .

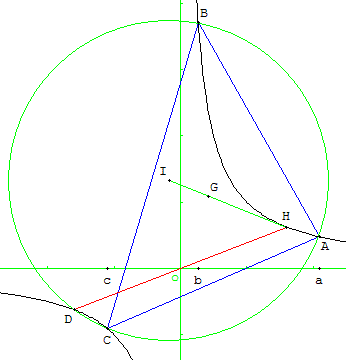
On désigne par a, b, c trois réels non nuls, deux à deux distincts, puis par A, B, C les points de G d'abscisses respectives a, b, c. Le point H est l'orthocentre du triangle ABC. On appelle C le cercle circonscrit au triangle ABC, son centre est le point E.
Le point D est le symétrique du point H par rapport à O.
Le but de l'exercice est d'observer la position de certains points de la figure et d’étudier celle du point H.

Indications

2. Démontrer la conjecture émise sur les coordonnées du point H.

H est situé sur la courbe G.

Sachant que les produits scalaires AH. = 0 et . = 0.

Avec les coordonnées A(a, 1/a) ; B(b, 1/b) ; C(c, 1/c) et H(h₁, h₂),
résoudre le système (linsolve avec Xcas) et trouver h₁ = −1/abc ; h₂ = − abc.

3. Proposer une démarche permettant de démontrer la (ou les) conjecture(s) faite(s) pour le point D (on ne demande
pas les calculs, mais uniquement le plan proposé).

D est à l'intersection de G et du cercle circonscrit à ABC.

Faire varier a, b, c et se contenter de la preuve par GéoPlan.
Sinon avec la relation d'Euler GH = 2 GI, I est le barycentre de (G, 3) ; (H, −1)
et I a pour coordonnées ((a+b+c + 1/abc)/2 ; (1/a+1/b+1/c + abc)/2).
Sachant que D a pour coordonnées (1/abc ; abc), on peut vérifier, avec GéoPlan, que ( (a+b+c − 1/abc)/2 ; (1/a+1/b+1/c − abc)/2) est de longueur égale au rayon du cercle circonscrit (peut-on faire le calcul, sachant que le rayon R est tel que abc = 4RS ?).

Télécharger la figure GéoPlan triangle_ds_hyperbole.g2w

Compétences évaluées
Compétences TICE
  • Construire une figure à l'aide d'un logiciel de géométrie dynamique ;
  • Tester une conjecture.

Compétences mathématiques
  • Connaître la notion de produit scalaire et ses propriétés.

Sujets de 2008 non retenus

15. Tangentes communes à deux courbes

Situation
On considère les représentations graphiques C et C’ de deux fonctions. L'objectif est de rechercher les tangentes communes à ces deux courbes.

Compétences évaluées
Compétences TICE
  • Représenter graphiquement des courbes et leurs tangentes en un point donné ;
  • Utiliser l'aspect dynamique du logiciel pour émettre des conjectures.

Compétences mathématiques
  • Lien entre dérivée en un point et tangente à la courbe représentative d'une fonction ;
  • Équation d'une tangente en un point de la courbe représentative d'une fonction.

27. Cercles et paraboles

Situation
Il s'agit de déterminer les conditions pour qu'une parabole et un cercle admettent une tangente commune en leur point de contact.

Voir : parabole
Tangente à une parabole : épreuve pratique 2007

Points équidistants d'une droite et d'un point : épreuve pratique 2008

Propriétés de la parabole : épreuve pratique 2009

Compétences évaluées
Compétences TICE
  • Construire une figure à l'aide d'un logiciel de géométrie dynamique ;
  • Conjecturer les positions relatives de deux courbes.

Compétences mathématiques
  • Mettre en équation un problème d'intersection ;
  • Résoudre une équation polynomiale.

46. Optimisation d'une aire

Situation
Le but est d'étudier les variations de l'aire d'un triangle inscrit dans une figure donnée et de rechercher la configuration rendant cette aire maximale.

Voir : triangle inscrit dans un carré

Compétences évaluées
Compétences TICE
  • Réaliser des constructions avec un logiciel de géométrie dynamique ;
  • Émettre des conjectures.

Compétences mathématiques
  • Calcul de longueurs et d'aires en géométrie plane ;
  • Lien entre dérivation et extremum ;
  • Résolution d'équations.

47. Étude d'un lieu géométrique

Situation
L'énoncé donne le programme de construction d'un triangle dont un sommet se déplace sur une droite donnée. Le problème conduit à étudier les diverses positions du cercle circonscrit à ce triangle et le lieu de son centre.

Voir : lieux de centres

Compétences évaluées
Compétences TICE

• Réaliser des constructions avec un logiciel de géométrie dynamique ;
• Visualiser le lieu d'un point ;
• Émettre des conjectures.

Compétences mathématiques

• Calculs en géométrie analytique ;
• Détermination d'un lieu géométrique.

48. Un problème de construction

Situation
Dans le plan, on considère un triangle ABC. On se propose de construire un carré inscrit dans le triangle.

Solution
Voir : homothétie
Exemple de sujet trop facile et classique : voir la géométrie à l'épreuve pratique de terminale S avec GéoPlan et GéoSpace.

Compétences évaluées
Compétences TICE
  • Réaliser des constructions avec un logiciel de géométrie dynamique ;
  • Émettre des conjectures.

Compétences mathématiques
  • Propriétés des transformations usuelles.

50, 52. Déformation d'une figure géométrique

Situation
L'objet de l'exercice est d'étudier les déformations d'un objet usuel en s'attachant en particulier au lieu de l'un des points de cet objet lors des déformations.

Compétences évaluées
Compétences TICE

• Réaliser une construction avec un logiciel de géométrie dynamique ;
• Reconnaître une courbe plane ;
• Représenter graphiquement une fonction.

Compétences mathématiques

• Déterminer des coordonnées de points dans le plan ;
• Caractériser l'appartenance à une courbe.

59. Suite définie géométriquement

Situation
À partir d'une figure géométrique simple, on définit un processus itératif de construction.
À chaque étape, on extrait une grandeur géométrique de la figure : on définit ainsi une suite numérique dont on étudie le comportement.

Voir : courbe des quatre chiens

Compétences évaluées
Compétences TICE
  • Déterminer les termes d'une suite ;
  • Reconnaître une courbe d'après son allure.

Compétences mathématiques
  • Étudier la convergence d'une suite définie par récurrence.

70. Étude d'un problème de géométrie dans le plan complexe

Situation
Dans le plan orienté, on considère deux points distincts O et A et le cercle de diamètre [OA]. Soit M un point de ce cercle, distinct de O et de A. On s'intéresse aux points images du point M par différentes transformations. Il s'agit de déterminer les lieux de ces différents points.

Compétences évaluées
Compétences TICE

• Réaliser des constructions avec un logiciel de géométrie dynamique ;
• Visualiser des lieux de points.

Compétences mathématiques

• Utiliser les transformations géométriques usuelles ;
• Élaborer une stratégie permettant de déterminer un lieu de points.

72, 78. Recherche d'un point fixe

Situation
Dans le plan orienté, on considère un triangle ABC et un cercle de centre A. Soit M un point de ce cercle, S une similitude et M’ le point image de M par la similitude S. Il s'agit d'étudier la position de la droite (MM’).

Compétences évaluées
Compétences TICE

• Réaliser des constructions avec un logiciel de géométrie dynamique ;
• Visualiser le lieu d'un point.

Compétences mathématiques (spécialité)

• Caractériser une similitude plane ;
• Utiliser des triangles semblables et des angles inscrits.

84. Extremum

Situation
On considère une fonction et sa courbe représentative.
Il s'agit de déterminer la position d'un point sur cette courbe qui optimise l'aire du domaine délimité par l'axe des abscisses, l'axe des ordonnées et la tangente en ce point.

Compétences évaluées
Compétences TICE

• Réaliser des constructions et des mesures avec un logiciel de géométrie dynamique ;
• Émettre et tester des conjectures.

Compétences mathématiques

• Faire le lien entre dérivée en un point et tangente à la courbe ;
• Élaborer une stratégie permettant de déterminer l'extremum d'une fonction.

95. Étude d'un lieu géométrique

Situation
Dans le plan orienté, un point M décrit un cercle. Une configuration géométrique varie avec le point M. À l'aide de transformations bien choisies, on recherche le lieu de points associés à M dans la configuration.

Compétences évaluées
Compétences TICE

• Construire une figure plane à l'aide d'un logiciel de géométrie dynamique ;
• Visualiser le lieu d'un point.

Compétences mathématiques (spécialité)

• Reconnaître des transformations usuelles dans une configuration ;
• Connaître les propriétés des translations et des rotations.

Sommaire 2008

Épreuve pratique

Épreuve pratique 2007

Épreuve pratique 2009

Épreuve pratique avec GéoSpace :Géométrie dans l'espace

Épreuve pratique Espace 2008

Épreuve pratique en 2° Rectangle inscrit dans un triangle

Lien

Frédérique Laroche

Revue SesaMath.net

La géométrie à l'épreuve pratique de terminale S avec GéoPlan et GéoSpace

Format PDF

Pubimath