 Descartes et les Mathématiques
Descartes et les Mathématiques
La géométrie dans l'espace en terminale S
Épreuve pratique de mathématiques supprimée
Mathématique avec GéoSpace en TS - Sujets 2007 et 2008 de géométrie dans l'espace à l'épreuve pratique.
Sommaire2004 24. Tétraèdre 2007 15. Distance de deux droites dans l'espace 23. Cube 33. Section plane d'un tétraèdre et optimisation d'une distance |
2008 29. Optimisation dans l'espace |
Sujets ÉduSCOL 2004
11. Plans perpendiculaires
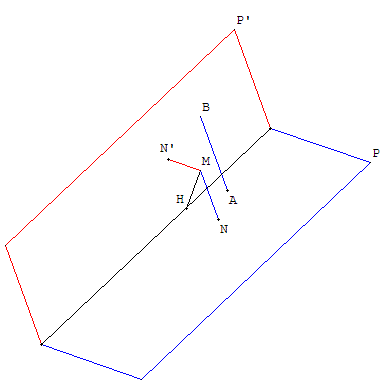
ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 11
L'espace est rapporté à un repère orthonormal (O, ![]() ,
, ![]() ,
, ![]() ).
).
• Déterminer une équation du plan P passant par le point A(1, 0, 1) et de vecteur normal ![]() (–1, 1, 1).
(–1, 1, 1).
• Soit P’ le plan d'équation x + 2y − z + 1 = 0 et M le point de coordonnées (0, 1, 1).
Sachant que deux plans sont perpendiculaires si un vecteur non nul normal à l'un est orthogonal à un vecteur non nul normal à l'autre, démontrer que les plans P et P’ sont perpendiculaires.
Calculer les distances d et d’ du point M aux plans P et P’ respectivement.
• Donner une représentation paramétrique de la droite D, intersection des plans P et P’.
Déterminer les coordonnées du point H de D tel que la droite (MH) soit perpendiculaire à la droite D.
Vérifier que MH2 = d2 + d’2.
![]() Télécharger la figure GéoSpace plans_perpendiculaires.g3w
Télécharger la figure GéoSpace plans_perpendiculaires.g3w
Indications
GéoSpace permet de créer la figure et de réaliser des calculs.
En plaçant le point B de coordonnées (0, 1, 2), le plan P est alors orthogonal au vecteur ![]() et a pour équation −x + y + z = 0.
et a pour équation −x + y + z = 0.
Le plan P’ a pour vecteur normal ![]() ’(1, 2, −1). Le produit scalaire
’(1, 2, −1). Le produit scalaire ![]() .
.![]() ’= −1×1 + 1×2 + 1×(−1) est nul, ces vecteurs sont orthogonaux et les plans P et P’ sont perpendiculaires.
’= −1×1 + 1×2 + 1×(−1) est nul, ces vecteurs sont orthogonaux et les plans P et P’ sont perpendiculaires.
Le point N, projection orthogonale de M sur P, a pour coordonnées (![]() ,
, ![]() ,
, ![]() ) car
) car ![]() est un vecteur directeur de la droite (MN) ; MN2 =
est un vecteur directeur de la droite (MN) ; MN2 = ![]() .
.
Le point N’, projection orthogonale de M sur P’, a pour coordonnées (−![]() ,
, ![]() ,
, ![]() ) ; MN’2 =
) ; MN’2 = ![]() .
.
Les équations paramétriques de la droite D sont : x = k, y = −![]() , z = k +
, z = k +![]() .
.
Le plan Q passant par M orthogonal à D a pour équation x + z = 1.
Pour k =![]() , on trouve le point H de coordonnées (
, on trouve le point H de coordonnées (![]() , −
, −![]() ,
, ![]() ) ; MH2 = 2. [HM] est la diagonale du rectangle MNHN’. MH2 = d2 + d’2 se vérifie par une relation de Pythagore.
) ; MH2 = 2. [HM] est la diagonale du rectangle MNHN’. MH2 = d2 + d’2 se vérifie par une relation de Pythagore.
24. Tétraèdre
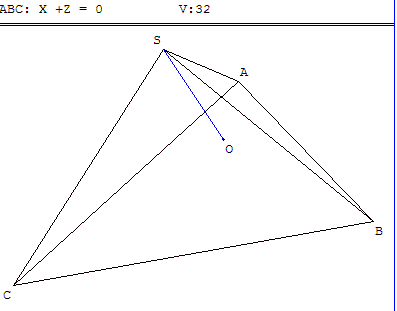
ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 24
L'espace est rapporté à un repère orthonormal (O ; ![]() ,
, ![]() ,
, ![]() ). On considère les points A, B, C et S de coordonnées respectives :
). On considère les points A, B, C et S de coordonnées respectives :
A(−1, 0, 1) ; B(1, 4, −1) ; C(3, −4, −3) ; S(4, 0, 4)
1. Démontrer que le triangle ABC est un triangle rectangle en A.
2. a) Montrer que le vecteur ![]() est orthogonal aux vecteurs
est orthogonal aux vecteurs ![]() et
et ![]() .
.
b) En déduire une équation cartésienne du plan (ABC).
3. a) Démontrer que le point O est le barycentre des points A, B, C, affectés de coefficients que l'on déterminera.
b) En déduire que le point O est situé dans le triangle ABC.
4. Calculer le volume V du tétraèdre SABC.
![]() Télécharger la figure GéoSpace tetraedre.g3w
Télécharger la figure GéoSpace tetraedre.g3w
Indications
![]() (2, 4, −2) ;
(2, 4, −2) ; ![]() (4, −4, −4) :
(4, −4, −4) : ![]() .
.![]() = 2 × 4 + 4 × (−4) + (−2) × (−4) = 0. Le produit scalaire est nul, les vecteurs sont orthogonaux. Le triangle ABC est un triangle rectangle en A.
= 2 × 4 + 4 × (−4) + (−2) × (−4) = 0. Le produit scalaire est nul, les vecteurs sont orthogonaux. Le triangle ABC est un triangle rectangle en A.
![]() (4, 0, 4) :
(4, 0, 4) : ![]() .
.![]() = 0 ;
= 0 ; ![]() .
.![]() = 0.
= 0. ![]() , orthogonal aux vecteurs
, orthogonal aux vecteurs ![]() et
et ![]() , est orthogonal au plan (ABC).
, est orthogonal au plan (ABC).
Un plan perpendiculaire au vecteur ![]() (a, b, c) a une équation de la forme ax + by + cz = d. Une équation du plan (ABC) est donc x + y = 0.
(a, b, c) a une équation de la forme ax + by + cz = d. Une équation du plan (ABC) est donc x + y = 0.
4![]() +
+ ![]() +
+ ![]() =
= ![]() , O est le barycentre de (A, 4) ; (B, 1) ; (C, 1). Les coefficients sont positifs, O est à l'intérieur du triangle. OS est une hauteur du tétraèdre.
, O est le barycentre de (A, 4) ; (B, 1) ; (C, 1). Les coefficients sont positifs, O est à l'intérieur du triangle. OS est une hauteur du tétraèdre.
V = ![]() s(ABC) × OS =
s(ABC) × OS = ![]() AB × AC × OS = 32.
AB × AC × OS = 32.
Sujets ÉduSCOL 2007
15. Perpendiculaire commune à deux droites
ÉduSCOL - Terminale S - Banque de sujets 2007 - Sujet 015
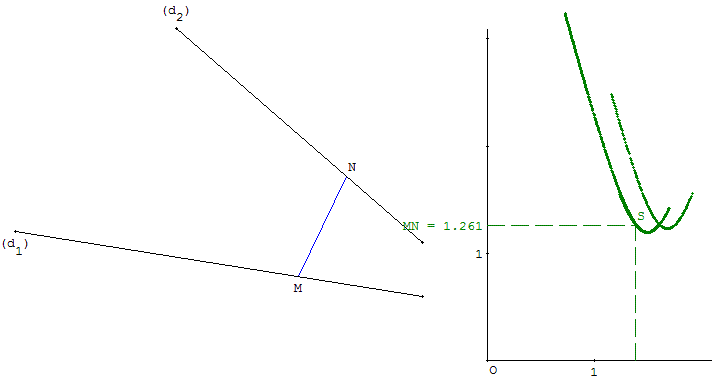
Situation
On définit, dans l'espace, deux droites particulières (d1) et (d2) non coplanaires.
On désigne par M un point variable de la droite (d1) et par N un point variable de (d2). Il s'agit de déterminer le minimum de la distance MN.
![]() Télécharger la figure GéoSpace dist_2_droites.g3w
Télécharger la figure GéoSpace dist_2_droites.g3w
Déplacer avec GéoSpace les points M et N afin de déterminer le minimum de la distance MN.
Commandes GéoSpace
Taper T pour activer le mode Trace du point S,
S, pour Sortir du mode trace,
P, pour tracer la perpendiculaire commune.
Déplacer les droites (d1) et (d2) en cliquant sur les extrémités des segments les représentant.
Fiche élève
- L'espace est rapporté à un repère orthonormal.
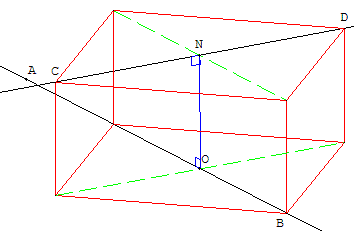
À l'aide d'un logiciel de géométrie dans l'espace, faire figurer les points A(−2 ; −2 ; 0) ; B(1 ; 1 ; 0) ; C(1 ; −1 ; 1) et D(−1 ; 1 ; 1), les droites (AB) et (CD),
un point M mobile sur la droite (AB) et un point N mobile sur la droite (CD). - Afficher la distance MN et essayer de placer des points M et N de façon à minimiser cette distance.
Donner une valeur approximative de cette distance minimale.
- Combien de couples de points (M ; N) répondant à cette condition de distance minimale semble-t-il y avoir ? Afficher les coordonnées de ces points.
- Quelles semblent être les positions respectives des droites (MN) et (AB) d'une part, et (MN) et (CD) d'autre part ?
Mettre en évidence cette conjecture, à l'aide du logiciel.
Calculer MN2 (on pourra écrire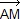 = t
= t 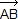 et
et 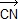 = k
= k 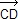 ).
).
Vos résultats confirment-ils certaines de vos conjectures ?
Indications
![]() =
= ![]() +
+ ![]() +
+ ![]() = − t
= − t ![]() +
+ ![]() + k
+ k ![]() avec
avec ![]() (3 ; 3 ; 0),
(3 ; 3 ; 0), ![]() (3 ; 1 ; 1) et
(3 ; 1 ; 1) et ![]() (−2 ; 2 ; 0),
(−2 ; 2 ; 0),
d'où ![]() (−3t + 3 − 2k ; −3t + 1 + 2k, 1)
(−3t + 3 − 2k ; −3t + 1 + 2k, 1)
et MN2 = (−3t + 3 −2k)2 + (−3t + 1 + 2k)2 + 12.
MN est minimal si −3t + 3 −2k = 0 et −3t + 1 + 2k = 0.
Ce système admet la solution t = ![]() et k =
et k = ![]() correspondant aux points M(0 ; 0 ; 0) et N(0 ; 0 ; 1).
correspondant aux points M(0 ; 0 ; 0) et N(0 ; 0 ; 1).
MN = 1 et ![]() (0 ; 0 ; 1) est orthogonal à
(0 ; 0 ; 1) est orthogonal à ![]() et
et ![]() ; la droite (MN) est la perpendiculaire commune à (AB) et (CD).
; la droite (MN) est la perpendiculaire commune à (AB) et (CD).
![]() Télécharger la figure GéoSpace dist_2_droites4.g3w
Télécharger la figure GéoSpace dist_2_droites4.g3w
Commentaires : les droites sont deux diagonales de faces d'un parallélépipède rectangle dont les côtés sont parallèles aux axes. Ces calculs sont un peu compliqués en regard de la facilité des droites données. Et encore, le texte original proposait O comme point A et le point de coordonnées (0 ; 0 ; 1) pour D : Quelle note mériterait l'élève qui, sans calcul, remarquerait que les deux droites sont contenues dans les plans d'équations z = 0 et z =1 ; OD =1, étant égal à distance des deux plans, est la distance minimale entre les deux droites ?
![]() Télécharger la figure GéoSpace dist_2_droites4.g3w
Télécharger la figure GéoSpace dist_2_droites4.g3w
Tracé de la perpendiculaire commune à deux droites
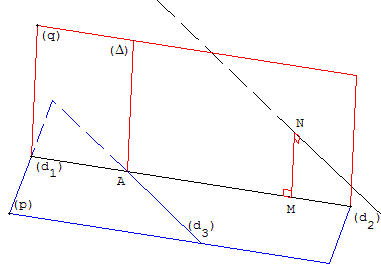
(d1) et (d2) étant deux droites non coplanaires de l'espace, il existe une droite et une seule, perpendiculaire à ces deux droites.
Pour la construire, la méthode consiste à choisir un point A sur (d1) et à tracer une droite (d3) parallèle à (d2) passant par A. Les droites (d1) et (d3) déterminent un plan (p) contenant A.
Soit (Δ) la perpendiculaire commune à (d1) et (d3) passant par A. (Δ) est la perpendiculaire en A au plan (p). (Δ) et (d1) déterminent un plan (q) perpendiculaire à (p).
Le plan (q) coupe (d2) en N. Dans le plan (q), la parallèle à (Δ) passant par N coupe (d1) en M.
(MN) est la perpendiculaire commune recherchée. MN est la distance minimale entre deux droites.
Commandes GéoSpace
Déplacer les droites (d1) et (d2) en cliquant sur les extrémités des segments les représentant.
Déplacer les profils des plans (p), (q) ou la marque (d3) en déplaçant leurs points d'ancrage.
![]() Télécharger la figure GéoSpace dist_2_droites2.g3w
Télécharger la figure GéoSpace dist_2_droites2.g3w
Compétences évaluées
Compétences TICE
• Construire une figure à l'aide d'un logiciel de géométrie dans l'espace ;
• Utiliser l'aspect dynamique pour faire des conjectures.
Compétences mathématiques
• Connaître la représentation paramétrique d'une droite ;
• Maîtriser l'orthogonalité dans l'espace.
19. Problème de Bergson
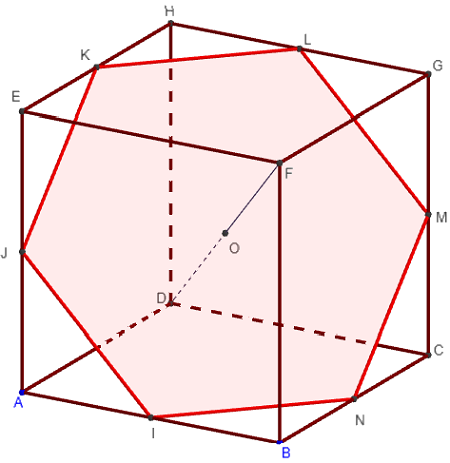
Problème donné au concours général de 1896 où Bergson eut le premier prix.
Les points I, J, K, L, M et N sont les milieux des arêtes du cube de centre O (cf. figure).
Quelle est la nature de l'hexagone IJKLMN ?
Indications
Il est facile de démontrer que les six segments sont égaux (à la moitié de la longueur d'une diagonale des faces du cube) et parallèle deux à deux :
par exemple (IJ) // (AC) // (EG) // (LM).
Dans un cube de côté 1, les côtés de l'hexagone sont de même longueur ![]() =
= ![]() .
.
19.a. En géométrie dans l'espace il faut montrer que les six points sont coplanaires : ils sont dans le plan (P) passant par O parallèle au plan (ACH).
Dans le rectangle ABGH, [IL] a pour milieu O est parallèle à [AH] donc [IL] est contenu dans le plan (P). Même
démonstration pour [JM] et [KN]. IJKLMN est donc contenu dans le plan (P) : c'est un hexagone régulier.
19.b. Une autre démonstration utilise le plan médiateur de [DF] comme plan (P) :
IF = ID comme hypoténuses de triangles rectangles ayant pour petits côtés un côté du cube et l'autre égal au demi-côté du cube. I est donc dans (P). De même pour J, K…
IJKLMN contenu dans le plan (P) est un hexagone régulier.
19.c. Aire de l'hexagone
L'hexagone est formé de six triangles équilatéraux de côtés ![]() .
.
La hauteur d'un de ces triangles mesure ![]() ×
× ![]() =
= ![]() / (2
/ (2![]() ).
).
L'aire de chaque triangle est ![]() ×
× ![]() ×
× ![]() / (2
/ (2![]() ) =
) = ![]() /8.
/8.
L'aire de l'hexagone est six fois cette aire, soit 6 ![]() /8 = 3
/8 = 3 ![]() /4.
/4.
![]() Figure 3D dans GeoGebraTube : hexagone de Bergson comme section plane du cube
Figure 3D dans GeoGebraTube : hexagone de Bergson comme section plane du cube
19.d. Calcul vectoriel et analytique
Soit ABCDEFGH un cube. On choisit le repère orthonormal (D ; ![]() ,
, ![]() ,
, ![]() ) avec
) avec ![]() =
= ![]() ,
, ![]() =
= ![]() et
et ![]() =
= ![]() .
.
On appelle I, J, K, L, M et N les milieux respectifs des segments [AB], [BC], [CG], [GH], [HE] et [EA].
– Déterminer les coordonnées des points I, K, M.
– Montrer que les six points I, J, K, L, M et N sont coplanaires, dans un plan que l'on notera (P) (on donnera une équation du plan (P) dans le repère choisi).
Montrer que le vecteur ![]() est un vecteur normal au plan (P).
est un vecteur normal au plan (P).
– Montrer que les projetés orthogonaux des points I, J, K, L, M et N sur la droite (DF) sont confondus en un même point. On appellera O ce point.
Déterminer la position du point O sur le segment [DF].
– Montrer que IJKLMN est un hexagone inscriptible dans un cercle dont on précisera le centre et le rayon et montrer que tous ses côtés ont même longueur.
– On considère la pyramide ayant pour base cet hexagone et pour sommet le point F.
Quelle fraction du volume du cube représente le volume de cette pyramide ?
Indications
Les coordonnées des milieux sont I(1, ![]() , 0) ; K(0, 1,
, 0) ; K(0, 1, ![]() ) et M(
) et M(![]() , 0, 1).
, 0, 1).
Le plan (P) a pour équation x + y + z = ![]() , ce plan est orthogonal au vecteur de coordonnées (1, 1, 1) : le vecteur
, ce plan est orthogonal au vecteur de coordonnées (1, 1, 1) : le vecteur ![]() .
.
L'hexagone régulier est situé sur un cercle de centre O, milieu de [DF], de rayon ![]() . La longueur des côtés est aussi
. La longueur des côtés est aussi ![]() .
.
L'aire de l'hexagone formé de six triangles équilatéraux de côtés ![]() est Sbase = 6 ×
est Sbase = 6 × ![]() .
.
La hauteur de la pyramide est OF = ![]() .
.
Le volume de la pyramide V est = ![]() × Sbase × hauteur =
× Sbase × hauteur = ![]() × (6 ×
× (6 × ![]() ) ×
) × ![]() =
= ![]() .
.
23. Orthogonalité dans le cube
23.a. Plan et droite orthogonaux dans le cube
Problème d'incidence
ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 23
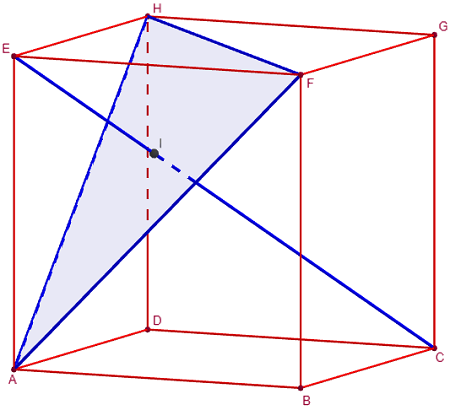
On considère un cube ABCDEFGH, d'arête de longueur a (a réel strictement positif).
Soit I le point d'intersection de la droite (EC) et du plan (AFH).
Montrer que la droite (EC) est perpendiculaire au plan (AFH).
Produit scalaire
1. Calculer, en fonction de a, les produits scalaires suivants :
![]() .
.![]() ,
, ![]() .
.![]() ,
, ![]() .
.![]()
2. En déduire que les vecteurs ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
On admettra, de même, que les vecteurs ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
3. En déduire que le point I est le projeté orthogonal de E sur le plan (AFH).
4. Justifier les résultats suivants : les droites (AF) et (EH) sont orthogonales, ainsi que les droites (AF) et (EI).
En déduire que la droite (AF) est orthogonale à la droite (HI).
Établir, de même, que la droite (AH) est orthogonale à la droite (FI).
5. Que représente le point I pour le triangle AFH ?
![]() Figure 3D dans GeoGebraTube : triangle équilatéral formé par trois diagonales de faces concourantes du cube
Figure 3D dans GeoGebraTube : triangle équilatéral formé par trois diagonales de faces concourantes du cube
Solutions - Problème d'incidence
La droite (HF) est orthogonale à (EC) :
Les deux diagonales (HF) et (EG) du carré EFGH sont perpendiculaires.
La droite (EA) perpendiculaire au plan EFH est perpendiculaire à la droite (HF) contenue dans ce plan.
La droite (HF) perpendiculaire aux droites (EG) et (EA) du plan AEG est perpendiculaire à ce plan.
(HF) est orthogonale à toute droite du plan AEG, en particulier à la droite (EC).
On démontre, de même, que la droite (AF) est orthogonale à (EC) : en effet, (AF) est perpendiculaire à (BE) et à (BC).
(AF) est donc perpendiculaire au plan EBC, et à la droite (EC) contenue dans ce plan.
La droite (EC) orthogonale aux deux droites concourantes (HF) et (AF) du plan AFH est orthogonale à ce plan.
Produit scalaire
![]() .
.![]() =
= ![]() .(
.(![]() +
+![]() ) = −
) = − ![]() 2 +
2 + ![]() .
.![]() = − a2+ 0 = − a2, car
= − a2+ 0 = − a2, car ![]() et
et ![]() sont orthogonaux,
sont orthogonaux,
![]() .
.![]() =
= ![]() .(
.(![]() +
+![]() ) = 0 +
) = 0 + ![]() 2 = a2,
2 = a2,
![]() est orthogonal au plan AEF, donc à
est orthogonal au plan AEF, donc à ![]() :
: ![]() .
.![]() = 0.
= 0.
![]() .
.![]() = (
= (![]() +
+![]() +
+![]() ).
).![]() = − a2 + a2 + 0 = 0,
= − a2 + a2 + 0 = 0, ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
La droite (EI) est perpendiculaire à la droite (AF).
La droite (EH) perpendiculaire au plan AEF est orthogonale à la droite (AF) contenue dans ce plan.
La droite (AF) perpendiculaire aux droites concourantes (EI) et (EH) est perpendiculaire au plan EHI contenant ces deux droites.
(AF) est perpendiculaire à la droite (HI) contenue dans ce plan.
Le point I intersection des hauteurs (HI) et (FI) du triangle AFH est l'orthocentre du triangle.
Les côtés du triangle AFH sont égaux comme diagonales des faces du cube de longueur a![]() , AFH est un triangle équilatéral, le point I est le centre du triangle.
, AFH est un triangle équilatéral, le point I est le centre du triangle.
Voir : produit scalaire dans l'espace
Sections planes d'un cube : l'espace en 3e, l'espace dans l'ancienne première S
23.b. Partage en deux d'un segment à l'intérieur du cube
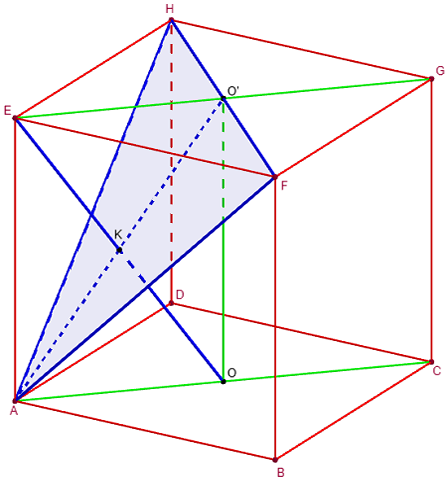
Plan coupant un segment en son milieu
Si O est le milieu du carré ABCD, la droite (EO) rencontre le plan (AFH) au point K.
Montrer que le point K est le milieu de [EO].
Indication
Si O’ est le milieu du carré EFGH, dans le plan (EAC) K est le point d'intersection des diagonales du rectangle EAOO’.
![]() Figure 3D dans GeoGebraTube : partage en deux d'un segment à l'intérieur du cube
Figure 3D dans GeoGebraTube : partage en deux d'un segment à l'intérieur du cube
Voir aussi coin de cube : cube en seconde
23.c. Partage en trois d'une diagonale du cube
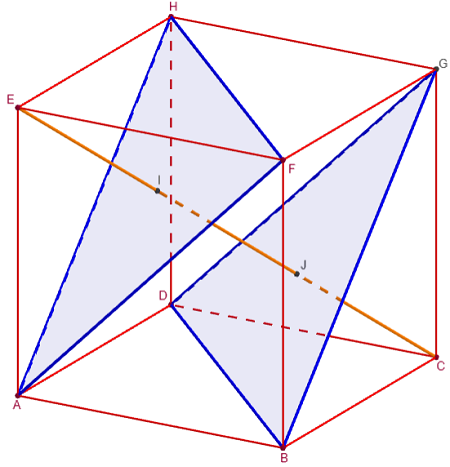
La droite (AF) perpendiculaire à deux côtés du triangle BCE est perpendiculaire au plan (BCE) et en particulier à la droite (EC).
De même, la droite (FH) perpendiculaire à deux côtés du triangle CEG est perpendiculaire au plan (CEG) et en particulier à la droite (EC).
(EC) perpendiculaire aux deux droites concourantes (AF) et (FH) est perpendiculaire au plan (AFH).
23.d. Généralisation
(EC) grande diagonale du cube est orthogonale aux plans (AFH) et (BDG). Ces deux plans sont parallèles.
La droite (EC) perce les triangles équilatéraux AFH et BDG en leurs centres I et J.
EI = IJ = JC.
![]() Figure 3D dans GeoGebraTube : partage en trois d'une diagonale du cube
Figure 3D dans GeoGebraTube : partage en trois d'une diagonale du cube
Généralisation : partage en trois d'une diagonale d'un parallélépipède
23.e. Brique de jus d'orange
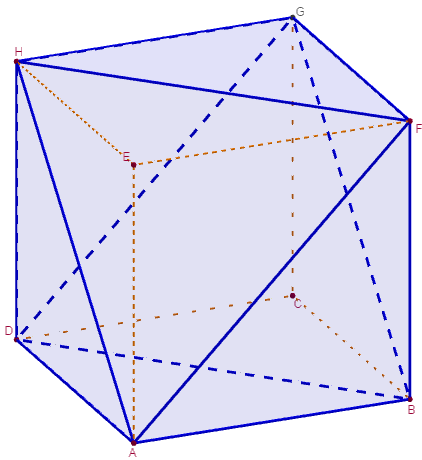
Jean Paul Guichard - Corol'aire 71 - décembre 2007
Pour lancer sa nouvelle marque de jus d'orange, un fabricant souhaite utiliser un emballage comme ci-dessus.
Le solide peut être considéré comme un cube dont on a ôté deux coins en forme de tétraèdre. La brique deux triangles équilatéraux comme bases et quatre demi-carrés comme faces latérales.
Quelle doit être, au mm près, la longueur de l'arête du cube pour que le volume de ce conditionnement soit d'un demi-litre ?
Soit a cette longueur, les coins de cube ont pour volume
![]() × Sbase × hauteur =
× Sbase × hauteur = ![]() , car Sbase est l'aire du demi-carré a2/2 et hauteur = a,
, car Sbase est l'aire du demi-carré a2/2 et hauteur = a,
le volume du solide est celui du cube moins deux fois celui des coins de cube : V = a3 − 2 ![]() =
= ![]() soit
soit ![]() .du volume du cube.
.du volume du cube.
Pour un volume de 0,5 L, on trouve a = 9,1 cm arrondi au mm le plus proche.
Pour la livraison, comment empiler ces briques dans un carton ?
![]() Figure 3D dans GeoGebraTube : brique de jus d'orange
Figure 3D dans GeoGebraTube : brique de jus d'orange
Descriptifs ÉduSCOL 2008
29. Optimisation dans l'espace
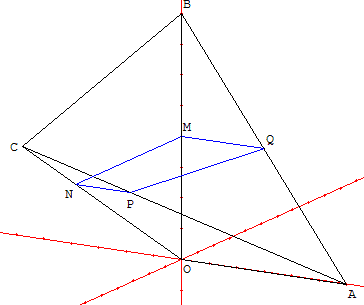
Situation
Il s'agit de déterminer à l'aide d'un logiciel de géométrie dynamique, quelle est la position d'un point mobile dans l'espace, qui rend maximale l'aire de la section d'un tétraèdre par un plan.
Énoncé
Dans l'espace rapporté à un repère orthonormal (O ; ![]() ,
, ![]() ,
, ![]() ) on considère les points A(0, 6, 0), B(0, 0, 8), C(10, 0, 8). M est un point appartenant au segment [OB]. Le plan (Π) passant par M et orthogonal à la droite (OB) coupe la droite (AC) en P.
) on considère les points A(0, 6, 0), B(0, 0, 8), C(10, 0, 8). M est un point appartenant au segment [OB]. Le plan (Π) passant par M et orthogonal à la droite (OB) coupe la droite (AC) en P.
Partie expérimentale
1. En utilisant un logiciel de géométrie, construire une figure traduisant l'énoncé.
2. On note respectivement N et Q les points d'intersection du plan (Π) avec les droites (OC) et (AB) et l'on admet que le quadrilatère MNPQ est un rectangle. En déplaçant le point M, émettre une conjecture quant à la position de ce point rendant maximale l'aire du rectangle.
On note t l'abscisse de M dans le repère (O, ![]() ).
).
En faisant bouger le point M, on conjecture que l'aire est maximum lorsque M est le milieu de OB (pour t = ![]() ).
).
![]() Télécharger la figure GéoSpace optimisation_espace.g3w
Télécharger la figure GéoSpace optimisation_espace.g3w
Démonstration
On note z = OM.
1. Exprimer en fonction de z les longueurs MN et MQ.
2. Démontrer la conjecture émise en 2
Compétences évaluées
Compétences TICE
- Réaliser une figure à l'aide d'un logiciel de géométrie dynamique dans l'espace ;
- Réaliser des affichages adaptés pour formuler des conjectures pertinentes.
Compétences mathématiques
- Choisir une méthode adaptée au problème posé et conduire les calculs à leur terme ;
- Déterminer le maximum d'une fonction numérique.
62. Tétraèdre trirectangle
Situation
Dans un tétraèdre, on étudie le lieu des projetés de l'un des sommets sur une droite variable, incluse dans la face opposée à ce sommet.
Énoncé
Dans l'espace rapporté à un repère orthonormé d'origine O, on construit le tétraèdre
OABC avec : A(2, 0, 0), B(0, 2, 0) et C(0, 0, 2).
Ce tétraèdre est dit « trirectangle » car trois de ses faces sont des triangles rectangles.
Pour tout point M du segment [AB], on construit le projeté orthogonal H
du point O sur la droite (MC).
Partie expérimentale
1. Proposer, à l'aide d'un logiciel de géométrie dynamique, une figure traduisant la situation et construire le lieu des points H lorsque le point M décrit le segment [AB].
Quel semble être le lieu du point H ?
2. Conjecturer les positions du point M sur le segment [AB] pour lesquelles la longueur CH semble maximale, minimale.
Compétences évaluées
Compétences TICE
- Réaliser une construction avec un logiciel de géométrie dynamique dans l'espace ;
- Reconnaître une courbe plane.
Compétences mathématiques
- Utiliser les projections orthogonales dans l'espace ;
- Calculer un produit scalaire dans l'espace ;
- Déterminer un extremum de fonction.
72. Étude de deux lieux géométriques
Situation
On considère un tétraèdre et un point M appartenant à une arête de ce tétraèdre.
Le but de l'exercice est d'étudier le lieu géométrique de deux points de la figure qui se déplacent lorsque M décrit un segment donné.
Énoncé
On considère un tétraèdre ABCD et un point I quelconque du segment [AB]. Le plan parallèle au plan (BCD) passant par I coupe la droite (AC) en J et la droite (AD) en K. On désigne par L l'isobarycentre des trois points I, J et K. On considère le point H projeté orthogonal du point C sur la droite (BL).
Le but de l'exercice est de déterminer le lieu géométrique du point L ainsi que celui du point H, lorsque le point I décrit le segment [AB].
Expérimentation
1. Réaliser à l'aide d'un logiciel une figure géométrique correspondant à cette situation.
2. Visualiser quelques positions du point L pour des positions différentes du point I sur
le segment[AB].
On aura intérêt à utiliser le mode « trace » si cette fonction est disponible dans le logiciel
utilisé.
Quel semble être le lieu géométrique du point L ?
3. Visualiser quelques positions du point H pour des positions différentes du point I sur
le segment[AB]. Quel semble être le lieu géométrique du point H ?
Démonstrations
4. Démontrer une des deux conjectures émises.
Compétences évaluées
Compétences TICE
- Constructions avec un logiciel de géométrie dans l'espace ;
- Visualisation d'un lieu de points.
Compétences mathématiques
- Propriétés du barycentre d'un système de points pondérés ;
- Utilisation des transformations géométriques usuelles ;
- Intersection de surfaces.
Table des matièresÉpreuve pratique 2009 : Cube et tétraèdre GéoSpace TS : Espace |
Géométrie plane à l'épreuve pratique de TS |
|
| |
|
|
Page no 134, créée le 9/12/2008, mise à jour le 31/8/2018 |