Descartes et les Mathématiques

Olympiades académiques 2008

Choix de sujets de géométrie des olympiades académiques de première et indications de solutions avec GéoPlan-GéoSpace

Cercles tangents

1. Deux cercles tangents, tangents à un carré

2. Cercle tangent à deux cercles tangents

3. Un problème d'Apollonius : cercle tangent à trois cercles

Sujets 2008 traités dans d'autres pages du site

Olympiades 2002 à 2005

Les olympiades académiques 2008
Brochure APMEP n^o 186

Les olympiades académiques 2009
Brochure APMEP n^o 190

Sujets 2008 traités dans d'autres pages du site

Un partage équitable

Sujet national

Transformer un quadrilatère en triangle

Amiens

Partage de l'angle d'un triangle en 4 : construction de-ci, de-là

Existe-t-il un triangle ABC tel que la hauteur, issue de A, la bissectrice de l'angle BÂC et la médiane relative au côté [BC] partagent l'angle BÂC en quatre angles de même mesure ?

Olympiades 2004 - Dijon

Réciproque : prouver qu'un triangle ayant angle partagé en 4 angles de même mesure par la hauteur, la bissectrice et la médiane, issues du sommet de cet angle, dans cet ordre, est obligatoirement rectangle.

Olympiades 2008 - Montpellier

Cloître

Construction d'une parabole, à la manière des compagnons bâtisseurs du Moyen-Âge.

Toulouse

Cercles tangents

1. Sangaku : deux cercles tangent inscrits dans un carré

Toutes séries ! Bordeaux

Sujet déjà posé à Poitiers aux olympiades 2002 (et au Kangourou en 2007).

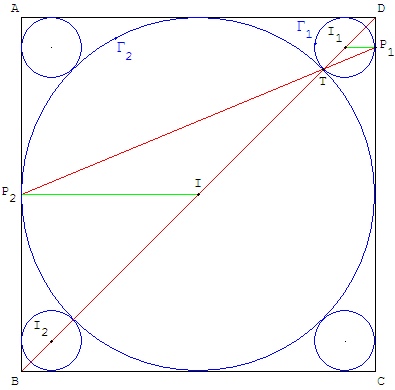
ABCD est un carré de côté a. Le cercle Γ₁ est tangent aux segments [AD] et [DC].

1. 1.a. Reproduire la figure 1 et construire un cercle Γ₂, contenu dans le carré ABCD, tangent à la fois au cercle Γ₁ et aux segments [AB] et [BC]. On indiquera le programme de construction.

1. 1.b. Expliquer pourquoi cette construction n'est pas possible sur la figure 2.

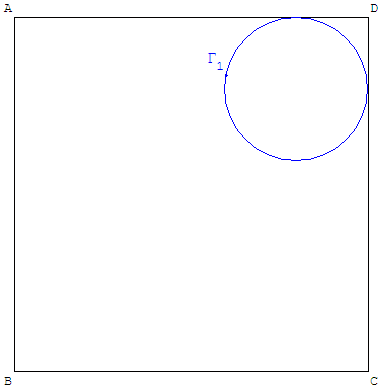
Figure 1

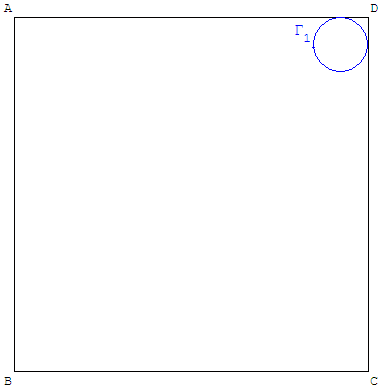
Figure 2

Trois cercles tangents dans un carré

Dans toute la suite de l'exercice on suppose que le cercle Γ₂ est contenu dans le carré ABCD, tangent à la fois au cercle Γ₁ et aux segments [AB] et [BC].
On désigne respectivement par R₁ et R₂ les rayons des cercles Γ₁ et Γ₂.

1. 2.a. Démontrer que R₁ + R₂ reste constant lorsque l'on fait varier les dimensions des deux cercles.

1. 2.b. Quelle est la valeur minimale et maximale de R₁ ?

1. 3. Soit S la somme des aires des disques limités par les cercles Γ₁ et Γ₂. Déterminer la valeur minimale et la valeur maximale de S.

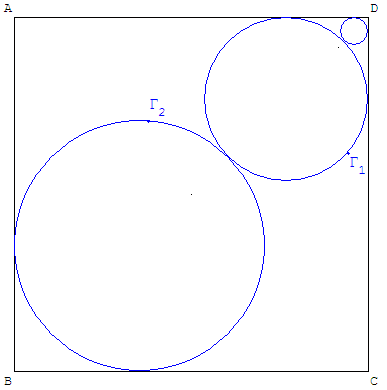
1. 4. Le petit cercle représenté sur la figure ci-contre est tangent au cercle Γ₁ et aux côtés [AD] et [DC].
Exprimer le rayon de ce cercle en fonction de R₁.

Indications avec une homothétie

Première construction, de la question 1. 1.a.

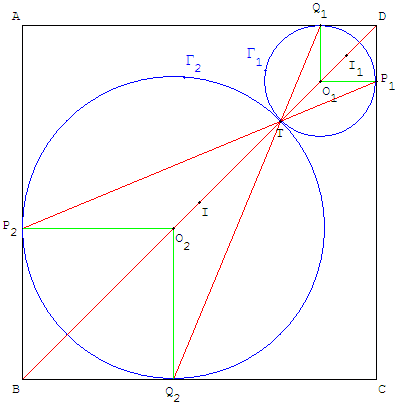
Les centres O₁ et O₂ des cercles étant à égale distance des côtés, ils sont situés sur la diagonale [BD] du carré. Soit I le milieu de [BD.

Pour n'importe quel point O₁ du segment [ID], les projections orthogonales P₁ et Q₁ de O₁ permettent de tracer le cercle Γ₁ de centre O₁ passant par P₁. Ce cercle, de rayon R₁= DP₁, coupe le segment [IO₁] en T.

L'homothétie de centre T, qui transforme D en B, transforme (DA) en (BC) et (DC) en (BA). P₁ et Q₁ ont pour images P₂ et Q₂, intersections des droites (P₁T) et (Q₁T) avec les deux côtés du carré.

Le cercle Γ₂ est l'image par cette homothétie du cercle Γ₁. On trouve son centre O₁ à l'intersection de la diagonale et de la perpendiculaire par exemple en P₂au côté (BA). Son rayon R₂= BP₂.

Cinq cercles et homothétie

Si BP₂ est supérieur à , alors R₂ > et le cercle Γ₂ n'est pas l'intérieur du carré, il ne convient pas.

La position limite est obtenue lorsque R₂ = . Le point de contact P₂ est le milieu de [AB]. La droite P₂T coupe le côté [CD] en P₁. R₁= DP₁ est la valeur minimale des rayons.
I₁ est la position extrême des centres des cercles Γ₁.

Le point O₁ doit rester sur le segment [II₁] pour la construction soit possible ce qui n'est pas le cas de la figure 2.

De même, O₂ appartient au segment [I₂I].

Constructions avec la tangente en T

Deuxième construction

Bissectrice de l'angle formé par deux tangentes

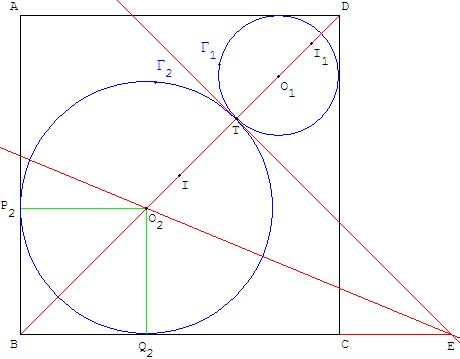
Le cercle Γ₁ de centre O₁ coupe le segment [IO₁] en T.
La tangente en T, perpendiculaire à (BD), coupe (BC) en E.
La bissectrice intérieure de l'angle BÊT coupe [BD] en O₂ centre du cercle Γ₂ cherché.

En effet les droites (ET) et (EB) sont tangentes au cercle Γ₂ et le centre est situé sur la bissectrice de l'angle formé par ces deux tangentes.

Troisième construction

Tangentes communes à un troisième cercle

Le cercle Γ₁ de centre O₁ coupe le segment [IO₁] en T.
La tangente en T, perpendiculaire à (BD), coupe (BC) en E.
Le cercle de centre E passant par T coupe [BC] en Q₂.

La perpendiculaire en Q₂ à (BC) coupe la diagonale [BD] en O₂.
Le point O₂ est le centre du cercle Γ₂ voulu.

En effet, les droites (O₂T) et (O₂Q₂) sont les deux tangentes au cercle de centre E, passant par T.
Les longueurs O₂T et O₂Q₂ sont égales, et sont égales au rayon de Γ₂.

Quatrième construction

Parabole lieu des centres

Le cercle Γ₁ de centre O₁ coupe le segment [IO₁] en T.

La parabole P est l'ensemble des centres M des cercles passants par le foyer T et tangents à la directrice (BC).

Le point O₂ est l'intersection de la parabole P avec la diagonale [BD] du carré.

Le point O₂ est le centre du cercle Γ₂ voulu.

Valeurs minimale et maximale des rayons et des aires

1. 2.a. Les rayons R₁ et R₂ des cercles vérifient :

DO₁ + R₁ + R₂+ O₂B = DB = a, avec DO₁ = R₁ et O₂B = R₂,

donc
(R₁ + R₂) (1 + ) = a.

C'est-à-dire : R₁ + R₂= a (2 - ).

1. 2.b. Les cercles étant situés à l'intérieur d'un carré de côté a, leurs rayons restent inférieurs à . Le minimum de R₁ est atteint lorsque R₂ est maximal égal à .
On en déduit que chaque rayon appartient à l'intervalle .

1. 3. La somme des aires des deux cercles est :

S = π(R₁² + R₂²) = [(R₁ + R₂)² - (R₁ - R₂)²] = [(6 - 4)a² - (R₁ - R₂)²].

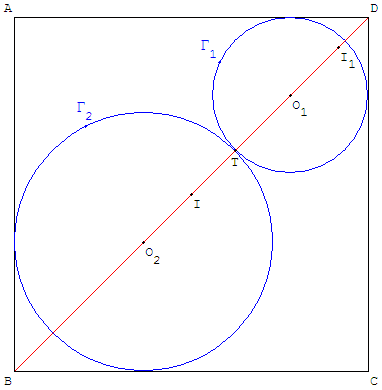
On en déduit immédiatement que cette aire est minimale quand :
R₁ = R₂= et vaut alors S_min = π(3 - 2 )a².
Le point T est le centre I du carré et les cercles Γ₁ et Γ₂ sont les cercles inscrits dans les triangles ADC et ABC.

L'aire est maximale quand R₁ est maximal et R₂minimal (ou inversement), c'est-à-dire quand R₁ = et R₂= .

On obtient alors S_max = [(6 - 4) a² - (-1 + )²a²] = (9 - 6)a².

Voir aussi : remplir un carré avec deux cercles de même rayon,

   Deux cercles de rayons l'un le double de l'autre : résoudre avec l'algèbre des problèmes de géométrie

   Les deux cercles dans le carré

Trois cercles tangents dans un carré

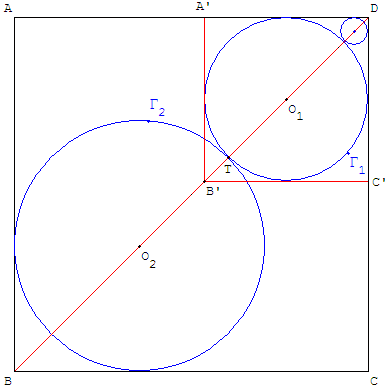
1. 4. Soit Γ₃ le petit cercle de centre O₃ représenté sur la figure ci-contre est tangent au cercle Γ₁ et aux côtés [AD] et [DC].

Le cercle Γ₁ est inscrit dans le carré A’B’C’D de sommet D.

Dans ce carré de côté a = 2R₁, Γ₃ est le cercle de rayon minimal R₃ = comme calculé ci-dessus.

Le rayon de ce cercle est donc R₃ = (3 - 2) R₁.

2. Cercle tangent à deux cercles tangents

Corse

Dans un repère (O, , ), on considère les points I(1, 0) et J(0, 1). Soit (C) le cercle de centre O et de rayon 1 et (C’) le cercle de diamètre [OI].

Dans cet exercice on étudie des cercles tangents intérieurement à (C) et tangents extérieurement à (C’) comme le montre cette figure.

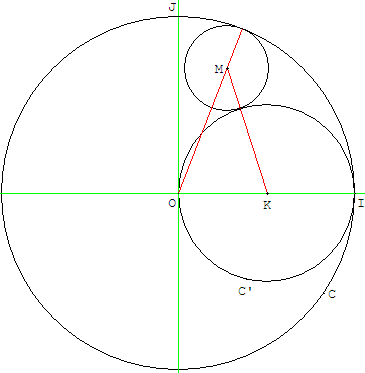
2. 1. Déterminer le rayon du cercle (C_A) tangent intérieurement à (C) et tangent extérieurement à (C’), dont le centre A est un point du segment [OJ].

2. 2. Déterminer le rayon du cercle (C_B) tangent intérieurement à (C) et tangent extérieurement à (C’), dont le centre B a pour abscisse .

2. 3. Soit M un point de coordonnées positives (x, y) centre d'un cercle (C_M) tangent intérieurement à (C) et tangent extérieurement à (C’) et à (C_A).
Déterminer le rayon de (C_M) et les coordonnées de son centre.

Cercle passant par un point tangent à deux cercles

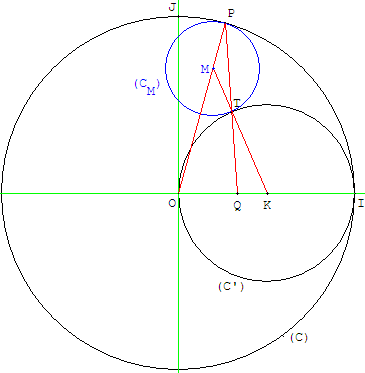
Cet exercice est un cas particulier de problème de contact PCC : construire le cercle (C_M) passant par un point P tangent à deux cercles (C) et (C’).

Soit Q le point de coordonnées (, 0). Une homothétie de centre Q de rapport -2 transforme le cercle (C’) en (C).

Un cercle (C_M) tangent intérieurement à (C) et tangent extérieurement à (C’) est globalement invariant
par l'inversion de pôle Q, de puissance k = 4/9, échangent les deux cercles (C’) en (C).

Les points de contact P et T sont alignés avec le pôle Q.

2. 1. Construire le cercle (C_A) tangent intérieurement à (C) et tangent extérieurement à (C’), dont le centre A est un point du segment [OJ] est tangent à (C) en J.

Le cercle (C_A) est tangent intérieurement à (C) au point J et tangent extérieurement à (C’) au point T situé sur le segment [QJ].
Le centre A est à l'intersection des droites (OJ) et (KT).

Le rayon de (C_A) est R = et son centre A a pour ordonnée .

Écrire la relation de Pythagore dans le triangle rectangle OAK sachant que :

OA = 1 - R ; OK = et KA = + R.

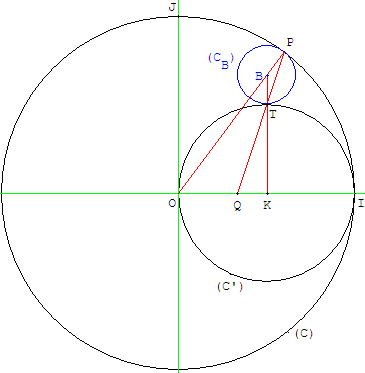
2. 2. Construire le cercle (C_B) tangent intérieurement à (C) et tangent extérieurement à (C’), dont le centre B a pour abscisse .

Le cercle (C_B) est tangent extérieurement à (C’) au point T abscisse . Il est tangent intérieurement à (C) au point P est situé sur le segment [QT].
Le centre B est à l'intersection des droites (OP) et (KT).

Le rayon (C_B) est R = et son centre B a pour ordonnée .

Écrire la relation de Pythagore dans le triangle rectangle OBK sachant que :

OB = 1 - R ; OK = et KB = + R.

3. Un problème d'Apollonius : cercle tangent à trois cercles

Cercles tangents dans un cercle

Sangaku

On aurait pu se contenter d'une simple vérification montrant que la somme des rayons des cercles (C_A) et (C_B) est égale à la distance AB entre les centres.

Beaucoup de calculs pour traiter analytiquement ce problème et on se prive de la deuxième solution qui était le symétrique de (C’), par rapport à O (voir les calculs dans la brochure APMEP).

En géométrie synthétique, on peut utiliser la méthode de Viète, assez difficile, présentée dans la page problèmes de contact :

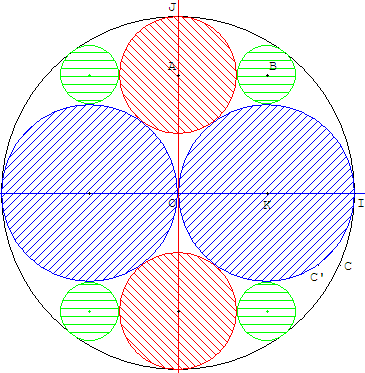
Soit R le rayon du plus petit cercle (C_A) des trois cercles donnés.
On substituera au cercle (C) une circonférence concentrique et rayon augmenté de R, et à (C’) une circonférence concentrique dont le rayon est diminué de R.
Avec les extrémités de deux rayons parallèles et de sens contraires, on trouve le centre S d'homothétie négative de ces deux cercles.

On se trouve dans le problème de contact PCC : tracer un cercle tangent à deux cercles de centres O et K passant par le centre A du dernier cercle.

Pour cela, on utilise l'inversion de centre S, qui, sur (OI), transforme les points Q₁ en Q₂.
Sur le cercle circonscrit à AQ₁Q₂ on trouvera le point A’, image de A par l'inversion, à l'intersection de la droite (SA).

Ce qui ramène au cas PPC : tracer un cercle passant par A et A’ et tangent en S₁ ou S₂ à un des cercles auxiliaires, en utilisant le point E de concours des tangentes.
Pour cela, choisir un point V sur le grand cercle. Le cercle circonscrit à VAA’ le recoupe en V’. Les droites (SA) et (VV’) se coupent en E. La tangente au cercle circonscrit donne la longueur des tangentes. Il suffit du cercle de centre E pour trouver les points S₁ et S₂. Diminuer de R les rayons des cercles circonscrits à AA’S₁ et AA’S₂ pour trouver les cercles (C_B) et (C_D) cherchés et leurs centres B et D.

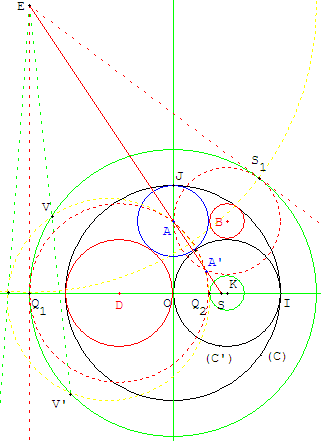
Cas particulier avec (C_A)

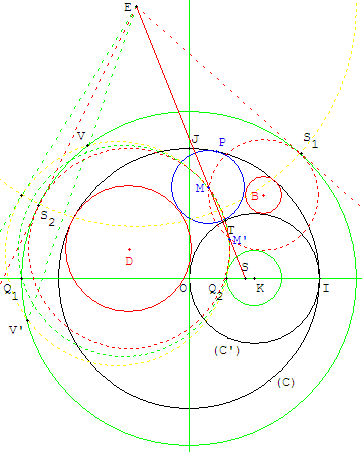
Cas général avec (C_M)

Télécharger les figures GéoPlan quatre_cercles_tangents.g2w, quatre_cercles_tangents_2.g2w

Table des matières

Google friendly

Dans d'autres pages du site

Faire de la géométrie dynamique en 1^ère S

Rectangle inscrit dans un rectangle