Descartes et les Mathématiques
Construction géométrique des nombres réels
Construire géométriquement les nombres rationnels et les racines de naturels sur la droite des réels.
Sommaire
1. a. Nombre rationnel a/b
b. Opérations : somme - produit - quotient
Racine d'un naturel
2. Naturel égal à une somme de carrés
3. Naturel égal à une différence de carrés
5. Racine de 7
6. Moyenne géométrique : puissance d'un point par rapport à un cercle
8. Construction d'un triangle rectangle d'un côté l'unité et d'hypoténuse 
Construction de réels
Sur la droite des réels, on peut construire les nombres rationnels et les racines de naturels.
1. Nombre rationnel a/b
Soit a un relatif et b un naturel non nul.
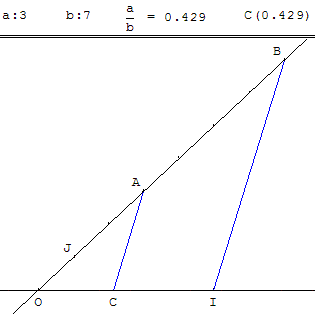
Sur une droite munie d'un repère (O, I), placer un point d'abscisse 
.
Figure pour un rationnel compris entre 0 et 1 :
Si n'est pas un décimal, réaliser la construction géométrique suivante :
Placer un point J à l'extérieur de la droite (OI) ;
sur la droite (OJ), muni du repère (O, J) placer les points A et B d'abscisses a et b.
La parallèle à (BI) passant par A coupe (OI) en C.
Comme les droites (AC) et (BI) sont parallèles, les triangles OCB et OIA sont semblables et on a l'égalité des rapports : 
.
D'où OC = 
.
Suivant le signe de a, on en déduit que C a pour abscisse .
Télécharger la figure GéoPlan fraction.g2w
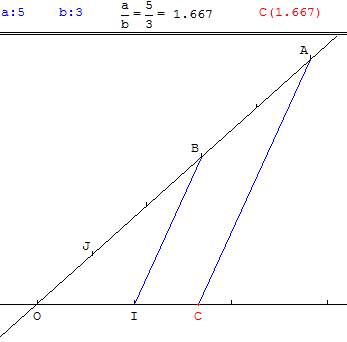
Rationnel plus grand que 1
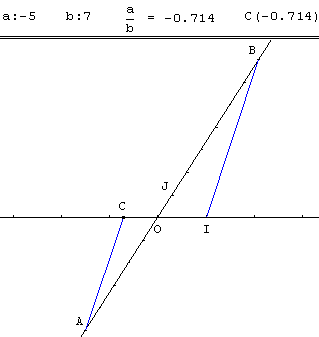
Rationnel négatif
1.b. Opérations : somme - produit - quotient
Construction à la règle et au compas de la somme, du produit et du quotient de deux nombres. (Les résultats de ces opérations sont constructibles.)
D'après une introduction géométrique du nombre - Xavier Gauchard - Plot no 18
Somme
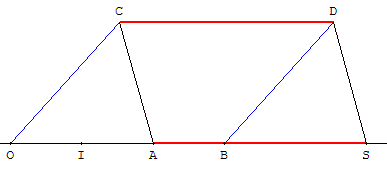
Sur la droite (OI), muni du repère (O, I) placer les points A et B d'abscisses a et b.
Placer un point C à l'extérieur de la droite (OI).
Le point D complétant le parallélogramme COBD permet de construire le vecteur 
= 
.
Le point S complétant le parallélogramme ACDS est l'image de A par la translation de vecteur .
L'abscisse s de S est égale à a + b.
Télécharger la figure GéoPlan somme.g2w
Thalès et construction de rectangles semblables
a et b sont deux nombres réels positifs.
Produit
Approche assez rare : le produit est construit comme une longueur et non comme une aire
Dans un repère orthonormé (O, I, J), tracer le rectangle OICB’ de longueur b et de largeur 1, son aire est b unités d'aire.
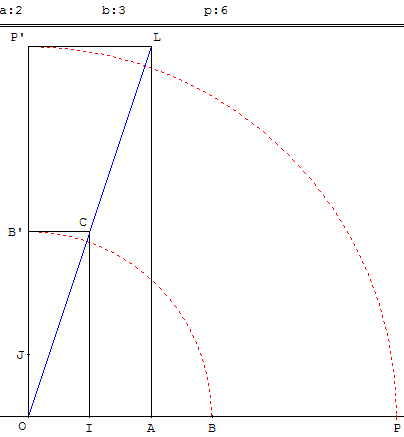
La diagonale (OC) rencontre la droite d'équation y = a en L.
A et L sont les images de I et C, par l'homothétie de centre O et de rapport a.
Le rectangle OALP, image de OICB’ par l'homothétie, est d'aire égale à b multiplié par a2, le carré du rapport d'homothétie, soit a2b.
Sa largeur est a, sa longueur est ab.
Télécharger la figure GéoPlan produit_1.g2w
Quotient
Dans un repère orthonormé (O, I, J), tracer le rectangle OBLJ de longueur OB = b et de largeur OJ = 1, son aire est b unités d'aire.
La diagonale (OL) rencontre la droite d'équation y = a en L.
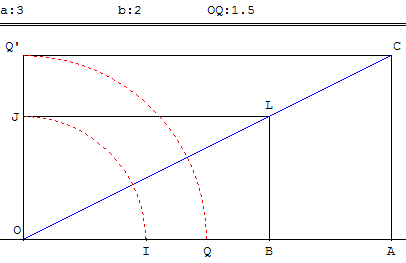
A et C sont les images de B et A, par l'homothétie de centre O et de rapport .
Le rectangle OACQ’ a une aire de b()2 = 
.
Sa longueur OA est a, sa largeur OQ’ est donc .
Télécharger la figure GéoPlan quotient_1.g2w
Voir : théorème de Thalès dans la Géométrie de Descartes
Autres triangles semblables
Produit
La figure ci-dessus est un cas particulier de la figure suivante :
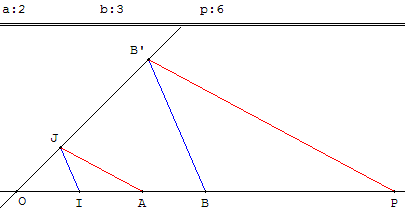
Dans un repère (O, I, J), placer les points A et B d'abscisses a et b.
La parallèle à (IJ) passant par B coupe (OJ) en B’,
la parallèle à (AJ) passant par B’ coupe (OI) en P.
Le point P a pour abscisse p = ab.
Se démontre avec Thalès ou avec l'homothétie de centre O de rapport b.
L'homothétie qui transforme I en B, transforme J en B’, la droite (JA) en (B’P) donc A en P.
De la relation vectorielle de l'homothétie 
= b 
,
on vérifie que OP = |b| OA = |ba|.
Télécharger la figure GéoPlan produit_2.g2w
Quotient
b ≠ 0
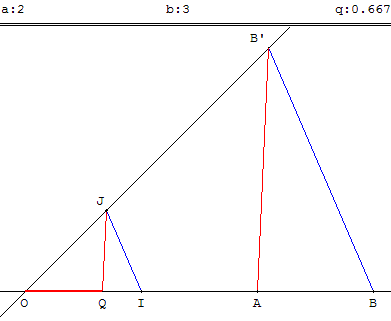
La parallèle à (IJ) passant par B coupe (OJ) en B’,
la parallèle à (B’A) passant par J coupe (OI) en Q.
Le point P a pour abscisse q = .
Preuves : Thalès ou l'homothétie de centre O, de rapport 
qui transforme B en I, B’ en J et A en Q.
Télécharger la figure GéoPlan quotient_2.g2w
Racine d'un naturel
2. Naturel égal à une somme de carrés
Utilisation de la propriété de Pythagore : construction de l'hypoténuse d'un triangle rectangle.
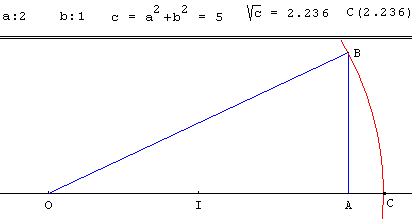
Soit un naturel c tel qu'il existe deux naturels a et b tels que c = a2 + b2.
Dans un repère (O, I, J) (orthonormé) placer les points A(a, 0) et B(a, b).
Le triangle OAB est rectangle en A et l'hypoténuse OB = c.
Le cercle de centre O, passant par B, coupe la demi-droite [OI] au point C d'abscisse 
.
Télécharger la figure GéoPlan racine_1.g2w
3. Naturel égal à une différence de carrés
Utilisation de la propriété de Pythagore : construction d'un des petits côtés d'un triangle rectangle.
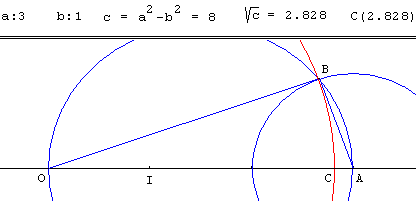
Soit un naturel c tel qu'il existe deux naturels a et b tels que c = a2 − b2.
Soit A le point abscisse a sur la droite munie du repère (O, I). Soit B un des points d'intersection du cercle de diamètre [OA] et du cercle de centre A et de rayon b.
Le triangle OAB est rectangle en B et le côté OB = c.
Le cercle de centre O, passant par B, coupe la demi-droite [OI] au point C, d'abscisse .
Télécharger la figure GéoPlan racine_2.g2w
4. Construction d'Euclide
Voici quatre figures montrant que la racine d'un naturel est constructible.
Moyenne géométrique - théorème de Thalès suisse :
Le carré de la hauteur issue de l'angle droit d'un triangle rectangle est égal au produit des longueurs des segments découpés sur l'hypoténuse.
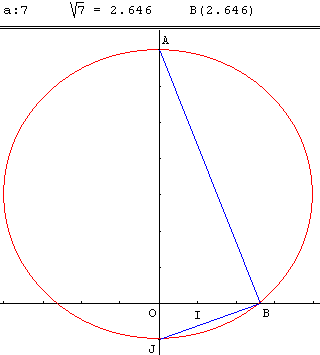
Dans un repère orthonormé placer sur l'axe des ordonnées les points J et A de part et d'autre de O tels que OJ = 1 et OA = a.
Le cercle de diamètre [AJ] coupe la demi-droite [OI) en B.
Le point B a pour abscisse 
.
La démonstration se fait dès la classe de 3e en remarquant que le triangle ABJ, inscrit dans un demi-cercle, est rectangle en B. Les tangentes des angles  et B des triangles rectangles semblables OAB et OBJ sont égales.
tan  = 
; tan B = 
,
d'où l'égalité des rapports
= .
Le produit des « extrêmes » est égal au produit des « moyens » :
OB2 = OA × OJ = OA × 1 = OA = a.
OB est la moyenne géométrique de OA et OJ : OB = 
= .
Remarque : comme dans la construction de Wallis ci-dessous, on retrouve la puissance du point O par rapport au cercle :
− OA × OJ = − OB2.
Télécharger la figure GéoPlan descartes.g2w
5. Racine de sept
Étant donné une longueur-unité, comment construire à l'aide d'une règle et d'un compas, un segment de longueur 
.
Comment, inversement, étant donnée une longueur égale à , retrouver avec quelle unité elle a été mesurée ?
Moyenne géométrique : construction d'Euclide reprise par Descartes
M:A.T.H. : Mathématiques Approchées par des Textes Historiques
IREM DE PARIS VII (1990).
À partir d'une unité a, construire le segment [BC] de longueur 7a et le point H à l'intérieur tel que BH = a. Tracer un demi-cercle de diamètre [BC].
La perpendiculaire en H à (BC) coupe le demi-cercle en A.
La longueur AH est égale à a.
Réciproque
Pour retrouver l'unité à partir d'une longueur
donnée, on utilise la même figure. On reporte la longueur sur la demi-droite [HA) de sorte que :
HD = .
La parallèle à (AB) issue de D coupe la droite (BC) en E.
EH est alors l'unité cherchée.
Télécharger la figure GéoPlan mon_369.g2w
6. Moyenne géométrique
Construction géométrique de la moyenne
6.a. Carré d'un petit côté d'un triangle rectangle
Dans un triangle rectangle, un côté de l'angle droit est moyenne proportionnelle entre l'hypoténuse et sa projection sur l'hypoténuse.
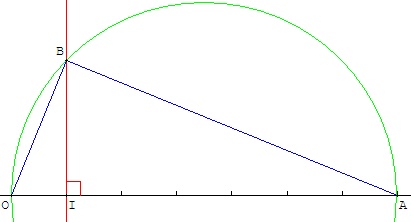
Sur une droite, munie du repère (O, I) placer le point A d'abscisse a = 7.
Tracer le cercle (c) de diamètre [OA] et la perpendiculaire en I à (OA).
Ce cercle et cette droite ont B comme point d'intersection.
[BI] et la hauteur du triangle rectangle ABO.
On a : OB2 = OI × OA = a, d'où OB = = .
Télécharger la figure GéoPlan moyen_geom2.g2w
6.b. Construction de Wallis - Puissance d'un point par rapport à un cercle
Notion disparue de l'enseignement français au lycée.
Construction de la moyenne géométrique en utilisant la puissance d'un point par rapport à un cercle.
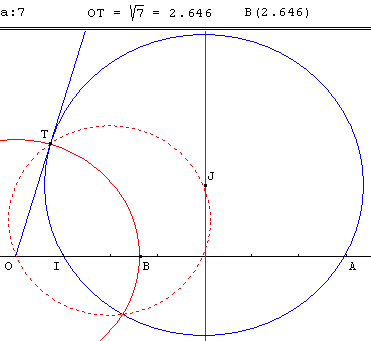
Sur une droite, munie du repère (O, I) placer le point A d'abscisse a = 7 et tracer un cercle (c) passant par I et A (le centre J est sur la médiatrice de [IA]).
Tracer une tangente à (c) issue de O : le point de contact T est une des intersections du cercle (c) et du cercle de diamètre [OJ].
La puissance d'un point O par rapport au cercle (c) est le produit OI × OA. Cette puissance est égale au carré de la longueur OT de la tangente au cercle issue de O :
OI × OA = OT2.
On a donc OI = 1 et OA = a = 7, d'où OT = = .
Le cercle de centre O, passant par T, coupe la demi-droite [OI] au point B, d'abscisse .
Télécharger la figure GéoPlan moyen_geom.g2w
7. L'escargot de Pythagore
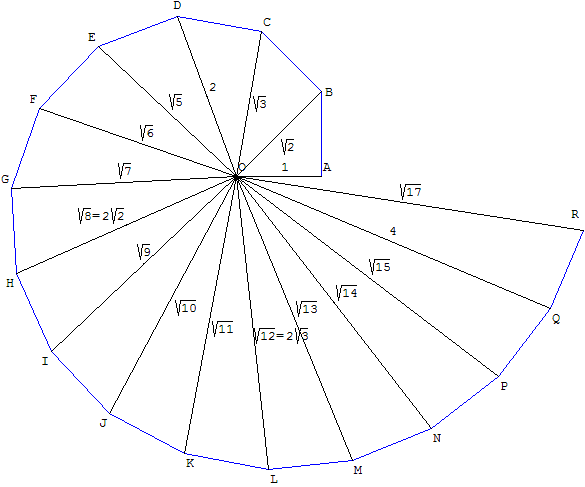
ou spirale de Théodore de Cyrène, géomètre grec, précepteur de Platon, de 465 à 398 avant J.-C.
Construction d'une spirale dont les longueurs des rayons forment la suite des racines des naturels.
Itérer la propriété de Pythagore :
on construit un triangle rectangle isocèle de petit côté égal à l'unité, puis
une suite de triangles rectangles tels qu'un côté de l'angle droit est l'hypoténuse du précédent,
l'autre petit côté étant de longueur égale à l'unité.
Le sixième triangle rectangle a une hypoténuse de longueur .
Nous avons dessiné 16 triangles.
Au 17e triangle, l'escargot de Cyrène fait un tour sur lui-même, en dépassant les 360°.
Télécharger la figure escargot_pythagore.g2w
Autres spirales : voir rectangle d'or
Image exportée dans WikiPédia : Théodore de Cyrène
8. Construction d'un triangle rectangle de petit côté l'unité et d'hypoténuse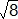
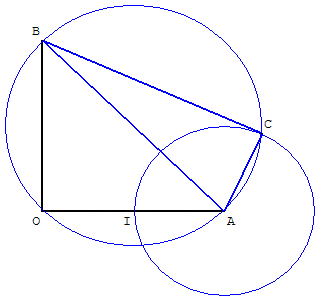
Construction d'un triangle rectangle ABC de petit côté l'unité et d'hypoténuse :
OI étant l'unité, construire le triangle rectangle isocèle OAB de petits côtés 2 unités.
C est un des points d'intersection du cercle de diamètre [AB] et du cercle unité de centre A.
Télécharger la figure GéoPlan mon_369c.g2w
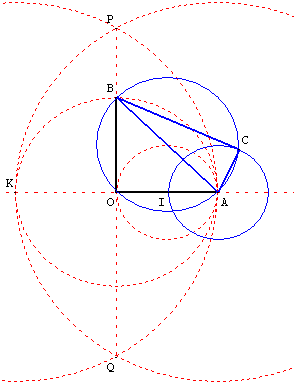
Construction à la règle et au compas du triangle OAB (voir : perpendiculaire élevée d'un point à une droite).
Réciproque
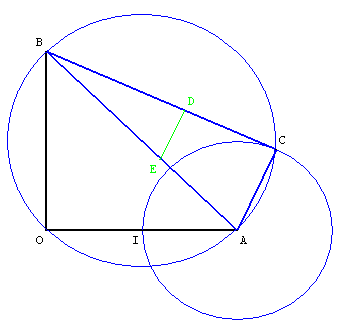
Construire un triangle rectangle ABC avec une longueur OI arbitraire,
placer le point D en reportant la longueur égale à sur la demi-droite [BC). La perpendiculaire élevée en D à (BC) coupe (AB) en E.
La longueur DE est l'unité cherchée.
Table des matières
Dans d'autres pages du site
Points et nombres constructibles
La géométrie en seconde
Téléchargement
Télécharger droite_reelle.doc : Google considère l'URL de ce document au format « .doc » comme une erreur de type "soft 404" !
Google friendly
|
|
Page no 75, réalisée le 15/9/2004 |