Descartes et les Mathématiques

Résolution graphique d'équations du second degré

Travaux pratiques de mathématiques en 1^ère S avec un logiciel de géométrie dynamique.

Sommaire

1. Construire deux segments connaissant la somme et le produit de leurs longueurs
2. Construire deux segments connaissant la différence et le produit de leurs longueurs

3. Orthogone de Lill

4. Méthode de K. Von Staudt

5. Cercle défini par un diamètre

On se propose de résoudre, par construction géométrique, des équations du second degré.
Les seules notions nécessaires sont : équations de droite, droites orthogonales, cercles et équation du second degré.

1. Construire deux segments connaissant la somme et le produit de leurs longueurs

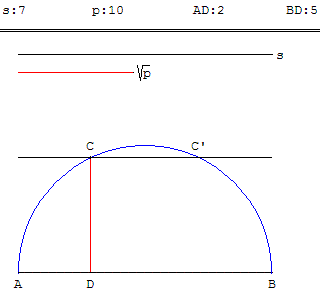
À partir d'un segment [AB] de longueur s, tracer le demi-cercle de diamètre [AB]. Si la droite située à une distance de (AB) coupe le demi-cercle en C, le triangle ABC est rectangle en C et la hauteur CD est moyenne proportionnelle entre AD et DB.

AD et DB sont les solutions de l'équation x² – sx + p = 0.

Leurs opposés sont les solutions de l'équation x² + sx + p = 0.

Télécharger la figure GéoPlan som_prod.g2w

2. Construire deux segments connaissant la différence et le produit de leurs longueurs

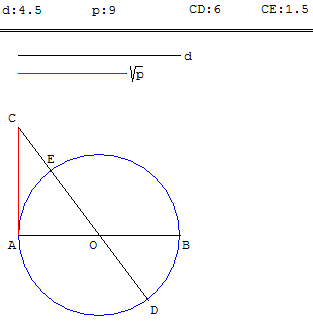
À partir d'un segment [AB] de longueur d, tracer le cercle de diamètre [AB] et de centre O.
Sur la tangente en A, placer le point C situé à une distance de A.
La droite (CO) coupe le cercle en D et E.
CD et CE sont solution du problème qui est toujours possible.
En effet, p = CD × CE = CA² est la puissance du point C par rapport au cercle
et CD – CE = DE = d.

CD et – CE sont les solutions de l'équation x² – dx – p = 0.
– CD et CE sont les solutions de l'équation x² + dx – p = 0.

3. Orthogone de Lill (1867)

Lill : capitaine du génie de l'armée autrichienne

Résoudre graphiquement l'équation ax² + bx + c = 0.

Depuis Descartes, on sait que les tracés de géométrie à la règle et au compas peuvent se réduire à des calculs, souvent du second degré, sur les nombres.
Ici la démarche est inverse. À partir de trois nombres a, b et c, placer trois points A, B et C, puis l'intersection d'un cercle, définit par son diamètre [IC], et de la droite (AB) permet de construire un orthogone pour trouver graphiquement les solutions de l'équation du second degré.
Lill trouve les deux solutions, lorsqu'elles existent, sur une même figure.

En fait, ce problème se résume à l'étude de triangles rectangles semblables OPI et AMI, puis AMI et BMN. Ici l'application du théorème de Thalès se fait simplement comme en troisième, en calculant la tangente de l'angle aigu Î de ces triangles.
En plus les solutions ne sont pas parachutées, mais la recherche est explicitée par une figure préliminaire, permettant, avec un minimum de culture mathématique, de comprendre les calculs.

Sinon il est possible de sauter la première étape et de passer directement aux applications du paragraphe d.
On pourra alors se contenter de la preuve par GéoPlan, en visualisant les calculs avec le logiciel.

3.a. Figure préliminaire

Éventuellement en modifiant tous les signes des coefficients a, b et c, on peut toujours supposer que a > 0.

Dans un repère (O, , ) orthonormal, on place les points I, A, B, C définis par :
  = ;  = a  ; = b ; = – c .
Les coordonnées des points sont alors :
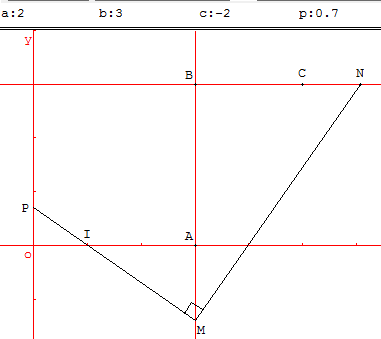
I(1, 0) ; A(1 + a, 0) ; B(1 + a, b) et C(a – c, b).

À tout point P situé sur l'axe des ordonnées, de coordonnées P(0; p), on associe un point N situé sur la droite (BC) construit de la façon suivante :

La droite (PI) coupe (AB) en un point M. La perpendiculaire en M à (PM) coupe (BC) en N.

3.b. Calculer les coordonnées de M et la longueur BN

Les triangles OPI et AMI ont leurs petits côtés parallèles aux axes. Ils sont donc rectangles respectivement en O et A. OÎP et AÎM, leurs angles aigus en I, sont égaux comme opposés par le sommet. Notons Î leur mesure ; le calcul de tan(Î) dans ces deux triangles permet d'écrire, lorsque p est positif :

tan(Î) =  =  soit  = , donc AM = ap.

Si P est sur [Oy), l'ordonnée de M est négative, comme a est supposé positif, le point M a donc pour coordonnées M(1 + a, – ap).

Dans l'autre cas, lorsque P est de l'autre côté par rapport à O, on peut encore vérifier que le point M a pour coordonnées M(1 + a, – ap).

Le triangle BMN, rectangle en B, a ses côtés perpendiculaires aux côtés du triangle AMI.
Les angles aigus Î = AÎM et BMN sont égaux et, si p > 0, on a tan(BMN) = tan(Î) = p.

D'où tan(BMN) =  =  =  = p.
Donc, BN = (ap + b) p = ap² + bp.
En vérifiant le sens des vecteurs, on voit que  dans tous les cas, on a  = (ap² + bp) .

3.c. Montrer que les points N et C sont confondus équivaut à ap² + bp + c = 0

Les N et C sont confondus si =  or  = – c , donc ap² + bp = − c soit ap² + bp + c = 0.

3.d. Résolution graphique de l'équation ax² + bx + c = 0

Quatre exemples de résolution de ax² + bx + c = 0

On trouve, graphiquement, les trois cas d'existence des solutions d'une équation du second degré :

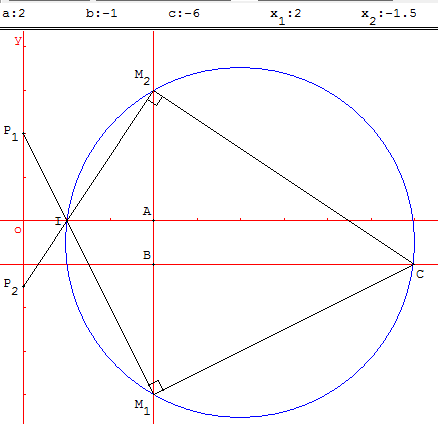
Application 1 : 2x² – x – 6 = 0

Orthogone IM₁CM₂

Les solutions de l'équation sont donc les « ordonnées » des points P pour lesquels la construction ci-dessus donne N = C.

En supposant que P (et donc M) existe, justifier que M appartient au cercle de diamètre [IC].

Indication

Si P existe, comme N = C, le triangle IMN est confondu avec le triangle rectangle IMC.

Ce triangle rectangle est inscrit dans un demi-cercle de diamètre [IC].

Application 2 : 4x² – 3x + 3 = 0

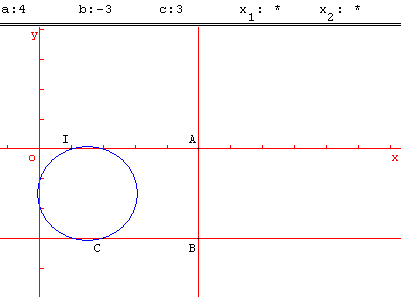
Lorsque le cercle de diamètre [IC] et la droite (AB) ont une intersection vide, l'équation :
    ax² + bx + c = 0 n'a pas de solution.

Figure GéoPlan

Modifier les coefficients avec les touches A, B ou C.

Taper 1, 2 ou 3 pour les applications 1, 2 ou 3.

Application 3 : 8x² – 2x – 3 = 0

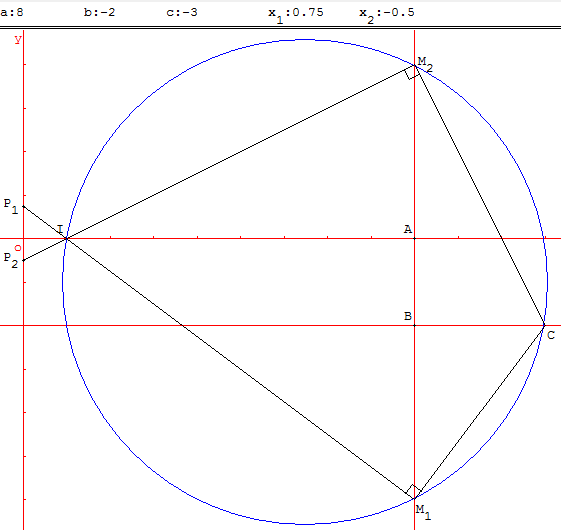
Applications 1 et 3

Orthogone IM₁CM₂ : lorsque le cercle de diamètre [IC] coupe la droite (AB) en deux points M₁ et M₂, la droite (IM₁) coupe l'axe (Ox) en P₁ et la droite (IM₂) coupe l'axe (Ox) en P₂. Les « ordonnées » x₁ du point P₁ et x₂ du point P₂ sont les deux solutions de l'équation :
    ax² + bx + c = 0.

Application 4 : ax² + bx + c = 0 avec Δ = b² – 4ac = 0

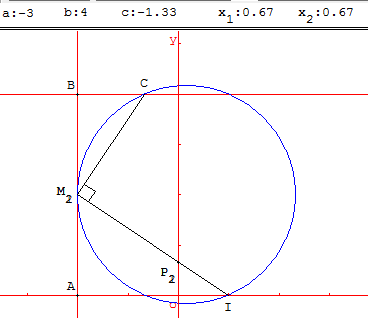
Application 4

Lorsque le cercle de diamètre [IC] est tangent à la droite (AB) en un point M ; les points M₁ et M₂ sont confondus en M, la droite (IM) coupe l'axe (Ox) en P = P₁ = P₂ et l'ordonnée x₁ = x₂ du point P est la solution double de l'équation :
    ax² + bx + c = 0.

4. Méthode de K. Von Staudt

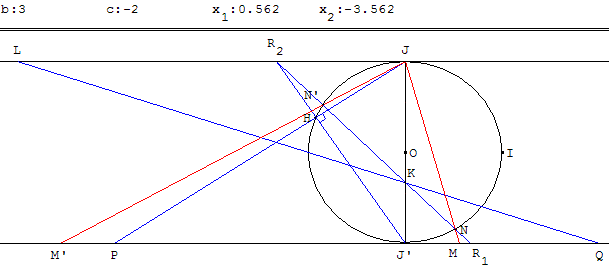
Résoudre graphiquement l'équation

x² + bx + c = 0.

Dans le repère (O, I, J) les droites (d₁) et
(d₂) sont tangentes au cercle unité en J’ et J.

Sur la droite (d₁) placer les points P et Q d'abscisses – b et – c,
puis sur (d₂) le point L d'abscisse – 4.

La droite (PJ) recoupe le cercle en H. La droite (JH’) coupe (d₂) en R₂.

La droite (QL) coupe (JJ’) en K. La droite (KR₂) coupe le cercle en N et N’.

Les droites (JN) et (JN’) coupent la droite (d₁) en M et M’.
Les abscisses x₁ et x₂ de M et M’ sont les solutions de l'équation du second degré.

5. Cercle défini par un diamètre

Adaptation d'« avec un quadrillage et une équerre » – Henry Plane – Plot n^o 17 – Premier trimestre 2007

Pour résoudre graphiquement l'équation x² + bx + c = 0, placer les points de coordonnées A(0, (– 1) ; P(– b, 0) et Q(– b, – c).
Les abscisses des points d'intersection du cercle de diamètre [AQ] avec l'axe (Ox), lorsqu'ils existent, sont les solutions de l'équation.

c < 0

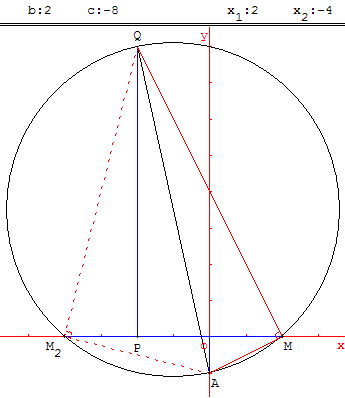
En effet, si M est un des points d'intersection du cercle et de l'axe des ordonnées.
Calculons AQ² de deux manières :
AQ² = AM² + MQ² = (AO² + OM²) + (MP² + PQ²)
    = AO² + OM² + ( + )² + PQ²
    = 1 + OM² + (b + )² + c²
    = 1 + 2OM² + 2b+ b² + c²

AQ² = ( + ) + OP² = (1 – c)² + b² = 1 – 2c + c² + b²

En égalant ces deux expressions, il vient :
1 + 2OM² + 2b + b² + c² = 1 – 2c + c² + b²,
soit 2OM² + 2b = − 2c et ² + b + c = 0

est une solution de l'équation étudiée.

On montre de même que l'ordonnée de M₂, deuxième point d'intersection du cercle et de l'axe (Oy), est l'autre solution de l'équation.

c > 0

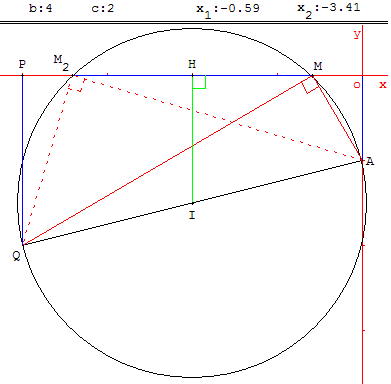
Discussion

Lorsque c est négatif, figure de gauche, A et Q sont de part et d'autre de l'axe (Oy), il y a deux intersections, donc deux solutions.

Lorsque c est positif, figure ci-dessus, A et Q sont dans le même demi-plan par rapport à (Oy), il n'y a intersection de l'axe et du cercle que si la distance de son centre I à (Oy) est inférieure à son rayon.

Distance de I à l'axe : IH = (OA + PQ) = |1 + c|

Rayon : IQ = AQ =

Il faut donc : |1 + c| ≤
ou (1 + c)² ≤ (1 – c)² + b²

On retrouve bien 4c ≤ b², soit Δ = b² – 4c positif.