Descartes et les Mathématiques

Pentagone régulier - Constructions approchées

La géométrie du pentagone et quatre constructions approchées

Sommaire

I. Propriétés du pentagone
1. Angles et côtés

2. Centre de gravité

3. Pentagone et nombre d'or

II. Constructions approchées
1. Méthode de Dürer

2. Construction des bâtisseurs du Moyen-âge

3. Construction dite « de Thalès »

4. Les étoiles de Compostelle

I. Propriétés du pentagone (figure géométrique)

1. Angles, côtés et diagonales

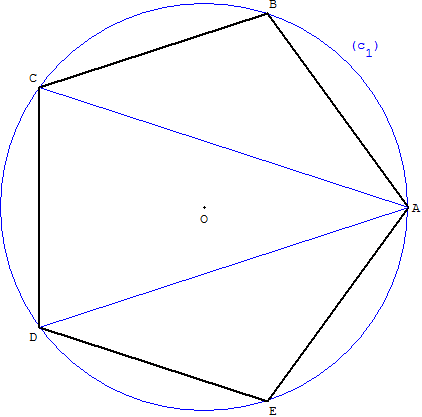
Angles du pentagone

L'angle au centre du pentagone régulier est de 72° et l'angle intérieur de 108°.

Longueur du côté du pentagone régulier

Si a est la longueur du côté, d la longueur d'une diagonale et r le rayon du cercle circonscrit, on a montré dans l'article polygones réguliers que :
a = 2 r sin 36° = = r ≈ 1,176 r.

Longueur de la diagonale du pentagone régulier

La longueur de la diagonale d'un pentagone régulier est sensiblement égale au rayon du cercle circonscrit multiplié par 1,9 :

d = = r ≈ 1,902 r.

La longueur de la diagonale d'un pentagone régulier est égale au côté multiplié par le nombre d'or :

Dans le triangle d'or ACD, le rapport est égal au nombre d'or φ = ;
d = a φ.

Figure interactive dans GeoGebraTube : pentagone régulier

Aire d'un pentagone

2. Isobarycentre du pentagone

O, intersection des axes de symétrie du pentagone régulier, en est le centre de gravité, donc : + + + + =  ;
en étudiant les abscisses, on trouve x_A + x_B + x_C + x_D + x_E = 0.

Choisissons un repère où est le vecteur unité de (Ox) : x_A = 1.

En raison de la symétrie de B et E, puis de C et D par rapport à (Ox) on a x_B = x_E, puis x_C = x_D, donc x_A + 2x_B + 2x_C = 0,
formule que l'on peut exprimer avec les cosinus : 1 + 2cos + 2cos = 0.

En posant x = cos , avec la formule de duplication, on trouve :

cos = 2cos² − 1 = 2 x² − 1.

Nous avons donc l'équation 4x² + 2x − 1 = 0. Elle permet de retrouver cos = solution positive de cette équation.

La solution négative est − = 2 cos² − 1 = cos .

3. Pentagone et nombre d'or

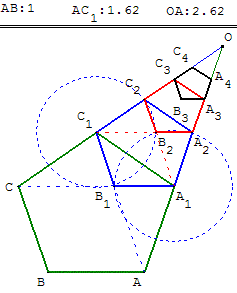
Soit ABCC₁A₁ un pentagone régulier.
On note c la longueur du côté de ce pentagone et d la longueur de la diagonale.
Soit B₁ le point d'intersection des diagonales (AC₁) et (A₁C).
Les points A₁, B₁ et C₁ sont les sommets du pentagone régulier A₁B₁C₁C₂A₂ de côté B₁C₁ = AC₁ − AB₁ = d − c et de diagonale A₁C = c.

Comme tous les pentagones réguliers sont semblables on a :

= = = .

Prendre c = 1 en choisissant la longueur AB comme unité. On a alors d = soit d² − d + 1 = 0.

La solution positive de cette équation est le nombre d'or φ = .
Dans tous les cas d = c  φ. Le pentagone A₁B₁C₁C₂A₂ est l'image du pentagone ABCC₁A₁ par l'homothétie de centre O et de rapport .

Si AA₁ = 1, A₁A₂ = = φ − 1; AA₂ = 1 + = φ.

Quand on itère cette homothétie, on obtient une suite infinie de pentagones. Observer la suite des points A, A₁, A₂…
A₂A₃ = = − φ + 2, A₃A₄ = = 2φ −3, A₄A₅ = = −3φ + 5 et ainsi de suite ;
voir TI-92 : nombre d'or et suite de Fibonacci.

AA_n = AA₁ + A₁A₂ + A₂A₃ + … + A_n-1A_n, somme des premiers termes d'une suite géométrique de raison , converge vers AO = 1 + φ.

II. Constructions approchées

II.1. Méthode de Dürer pour tracer le pentagone

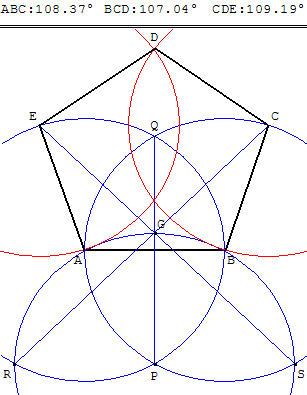
Construction approchée, à la « règle et au compas », du pentagone régulier.

« Albert Dürer (né à Nuremberg en 1471, mort en 1528) appartient, comme Léonard de Vinci, à cette génération de grands artistes, peintres, sculpteurs et architectes, pour lesquels la géométrie est non seulement un instrument d'analyse, mais un puissant moyen de perfectionnement. L'étude de la perspective le conduisit à la transformation des figures en d'autres figures du même genre. Et de là naquirent plusieurs méthodes géométriques, comme celle qui consiste à faire croître proportionnellement les ordonnées des points d'une figure, dans le dessin d'un profil dont on veut rendre les dimensions en hauteur plus facilement appréciables. Dürer maniait très habilement le compas pour tracer des ellipses et d'autres figures géométriques. Le pentagone de Dürer est un pentagone, construit avec une seule ouverture de compas ; mais d'autres géomètres ont démontré depuis que ce pentagone n'a pas tous les angles égaux et que sa figure n'est qu'approximative. »

Source : Ferdinand Hoefer, Histoire des mathématiques, Paris, Hachette, 1874, p. 337

ABCDE pentagone de Dürer

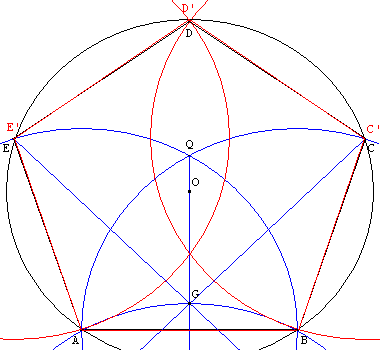
ABC’D’E’ pentagone régulier

Placer deux points A et B. À partir de ce segment [AB], qui sera un côté du pentagone, on trace cinq cercles de même rayon :
Tracer les cercles de centre A passant par B et de centre B passant par A. Ces deux cercles se coupent en P et Q.
Le cercle de centre P passant par A (et par B) coupe les deux premiers cercles en R et S, et le segment [PQ] en G.
La droite (SG) coupe le premier cercle en E (voir figure) et (RG) coupe le deuxième cercle en C.
Le dernier point D se trouve à l'intersection des cercles de centre E passant par A et de centre C passant par B.

Le pentagone ABCDE a ses cinq côtés égaux. L'erreur sur les angles est d'un demi-degré à un degré et demi. Le point D est très légèrement au-dessous du point exact D’ du pentagone régulier. Télécharger la deuxième figure pour mieux percevoir la différence avec GéoPlan.

II.2. Construction des bâtisseurs du Moyen-âge

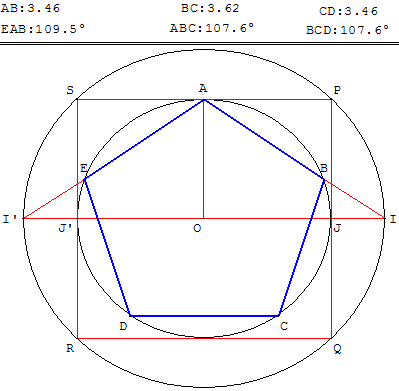
ABCDE mauvais tracé

Image de l'harmonie et de la logique grecque

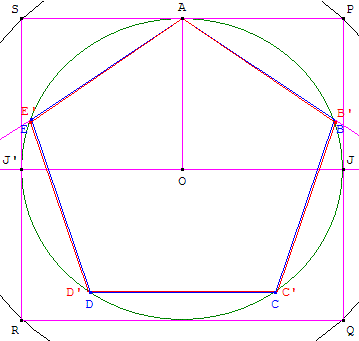
AB’C’D’E’ pentagone régulier

Tracé d'un pentagone de centre O et de sommet A par les bâtisseurs du Moyen-âge

Voir les figures ci-dessus.

Expliquer pourquoi cette figure n'est qu'une construction approchée du pentagone régulier :
dans le triangle rectangle OAI, tan OÂI = = . Le point B est très légèrement en dessous du point exact B’ du pentagone régulier.

II.3. Construction dite « de Thalès »

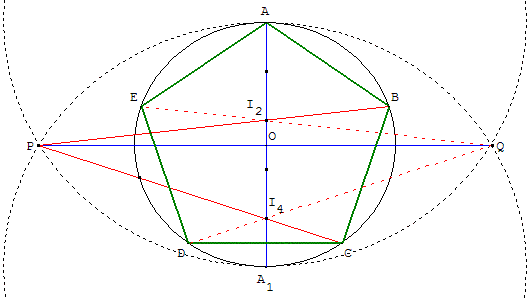
Cette construction d'un pentagone presque régulier est attribuée au mathématicien et philosophe grec Thalès de Milet (vers 600 avant J.-C.).
Elle nécessite la règle et deux ouvertures de compas.

Deux points A et A₁ étant donnés, tracer le cercle (c) de diamètre [AA₁]. Les cercles de centres A et A₁ et de rayon AA₁ se coupent en P et Q.

On divise le diamètre [AA₁] en n = 5 parties égales.

Les droites (PI₂) et (PI₄) rencontrent le cercle (c) en B et C, sommets du polygone. Ici on le complète par symétrie par rapport à (AA₁).
On obtient les points D et E intersections du cercle (c) et des droites (QI₄) et (QI₂).

Construction d'un polygone de n côtés

Cette méthode s'applique à un polygone régulier de n côtés.
Elle est d'une grande facilité et d'une précision très satisfaisante jusqu'à n = 10.

II.4. Les étoiles de Compostelle

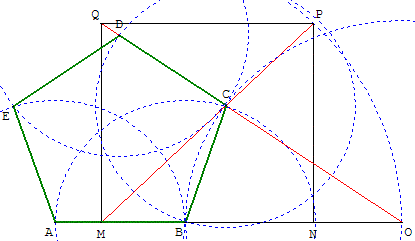
Tracer les points M et N, puis le carré MNPQ. Le cercle de centre M passant par P coupe la demi-droite [MN) en O.
La droite (OQ) coupe la diagonale [MP] du carré en C
Le cercle de centre O, passant par C, coupe [MN] en B. [BC] est un premier côté du pentagone.
Le cercle de centre B, passant par C, coupe [NM) en A, sommet du pentagone.
Le cercle de centre C, passant par B, coupe [CQ) en D, quatrième sommet du pentagone.
On termine le pentagone en trouvant l'intersection E des cercles de même rayon, de centres A et D.

Le pentagone ABCDE a ses cinq côtés égaux. L'erreur sur les angles est de 1 à 2 degrés.

Voir : Henri Vincenot - Les étoiles de Compostelle - Denoël - Folio

Origami du pentagone
    Pliage et nœud

    Construction approchée par pliage d'une feuille A4

Constructions exactes du pentagone

Constructions du pentagone avec quatre règles à bords parallèles

Nombre d'or

    Rectangle d'or

    Triangle d'or

Suites et TI-92 : Pentagone, nombre d'or et suite de Fibonacci

Avec GeoGebra : pentagone

cos

Pavage avec des pentagones

Moteur de recherche

Yahoo

Expressions clés

Pentagone régulier, géométrie pentagone,longueur de la diagonale d'un pentagone régulier,propriété pentagone

Copie

lerepairedessciences.fr/sciences/maths/pentagone.htm
Copyright abusivement attribué à S. Bourdreux
Où Google référence mieux la copie que l'original !

Copyright 2003 - © Patrice Debart

Mobile friendly