Descartes et les Mathématiques
Pavages du plan
Pavages avec des triangles et rectangles d'or ; pavages avec des pentagones, des hexagones.
Sommaire
1. Patchwor
2. Pavage non périodique du plan – Rectangle d'or
5. Pavage semi-régulier de Diane
Puzzle dans d'autres pages du site
Composer un carré de cinq carrés égaux
Configurations du plan en seconde :
Puzzle et triangle isocèle
Puzzle et carrés
Démonstrations géométriques de Pythagore :
Puzzle chinois
Puzzle de Périgal
1. Patchwork
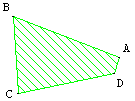
Est-il possible de réaliser un patchwork avec des pièces de tissus, ayant tous la forme de ce quadrilatère convexe. Il s'agit d'obtenir un grand morceau de tissu plan, sans laisser de vide et sans que deux morceaux se recouvrent.
Solution
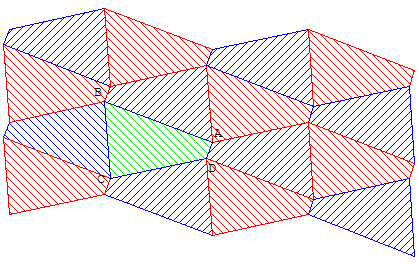
Il est possible de paver le plan avec n'importe quel quadrilatère convexe.
Il suffit de construire les symétriques du morceau initial par rapport au milieu de chacun de ses quatre côtés et de réitérer l'opération.
Télécharger la figure GéoPlan mon_394.g2w
2. Pavage non périodique du plan - Rectangle d'or
Extrait de la page : nombre d'or
Il est possible de paver le plan à partir de rectangles d'or. Ce pavage non régulier est formé de rectangles de plus en plus grands.
Une bonne occasion d'utiliser la fonction de création itérative de GéoPlan :
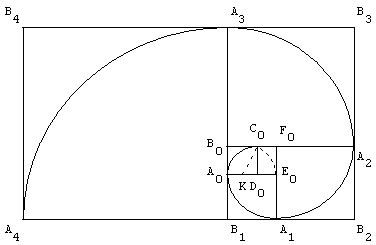
Tracer un rectangle d'or initial A0B0F0E0 à partir du carré A0B0C0D0. Tracer A0E0A1B1. B0F0A1B1 est un rectangle d'or. Remplacer A0, B0, F0, E0 respectivement par C1, F1, E1, D1 pour obtenir le rectangle d'or A1B1F1E1 contenant le carré A1B1C1D1 de niveau 1. Avec la commande d'itération (touche S) on tracera les carrés suivants.
En traçant dans chaque nouveau carré le quart de cercle de centre Dn, reliant AnAn+1, on obtient la spirale d'or C0A0A1A2…
Télécharger la figure GéoPlan rect_or2.g2w
3. Pavage de triangles d'or
Il est possible de paver le plan à partir de triangles d'or. Ce pavage non régulier est formé de triangles de plus en plus grands.
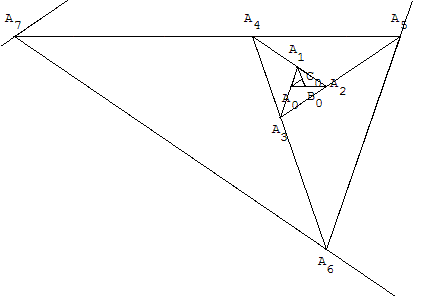
À partir du triangle AnAn+1An+2 créer le point An+3 tel que An+1AnAn+3 soit une section d'or et recommencer.
Encore une occasion d'utiliser la fonction de création itérative de GéoPlan :
tracer un triangle d'or initial A0B0C0. Trouver le point A1 tel que B0C0A1 forme une section d'or. Remplacer A0 et B0 respectivement par B1, C1 pour obtenir le triangle d'or A1B1C1 de niveau 1. Avec la commande d'itération (touche S) tracer les triangles suivants.
Télécharger la figure GéoPlan tria_or5.g2w
4. Cabri - Pavage d'hexagones réguliers : Méthode 1 par approximation
Les figures n'ont pas encore été transférées de l'ancien site Orange
Créer trois centres O, O’ et O” et un point A.
Avec la macro hexagone construire les hexagones de centres O, O’ et O” passant par A.
Déplacer les centres O’ et O” pour faire coïncider les côtés des hexagones.
Puis construisez d'autres hexagones à partir de nouveaux centres.
Méthode 2 par symétries
On constate dans la méthode précédente que les centres sont symétriques par rapport aux côtés des hexagones.
On peut donc créer le centre O et un point A. Avec la macro hexagone construire l'hexagone de centre O, passant par A. Construire le symétrique O’ du point O par rapport au segment [AB].
Avec la macro hexagone construire l'hexagone de centre O’, passant par A.
Puis construire de nouveaux symétriques des centres par rapport aux côtés des hexagones et d'autres hexagones à partir de ces nouveaux centres.
5. Pavage de Diane
Rosace du temple de Diane à Nîmes.
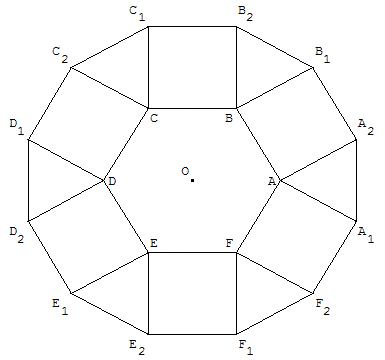
Reproduire cette rosace : les triangles compris entre deux carrés sont équilatéraux.
Télécharger la figure GéoPlan pi_diane.g2w
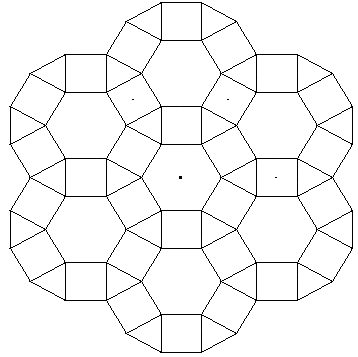
Pavage semi-régulier formé d'hexagones réguliers, de carrés et de triangles équilatéraux.
Très belle illustration : Mathcurve
Télécharger la figure GéoPlan pi_diane_2.g2w
6.Cabri : pavages avec des pentagones
En s'inspirant du Dictionnaire
Penguin des curiosités géométriques de David Wells (éd. Eyrolles) Roland Baboud a proposé, dans le bulletin n° 423 d'octobre 1999 de l'APMEP (Association des Professeurs de Mathématiques), quatre types de pavages pentagonaux, ainsi que la procédure pour construire
le «pavé» élémentaire. De tels pavages peuvent servir de points de départ à bien des activités
géométriques et calculatoires, avec différents niveaux d'exigence, depuis la simple réalisation de dessins jusqu'à la justification
précise de leur qualité de « paveurs ». Sans parler de la recherche d'autres pavages…
Les quatre paragraphes qui suivent sont l'illustration de cet article avec Cabri-géomètre.
6.a. Pavage du Caire
Pavage pentagonal semi-régulier uniforme
Motif de base du pavage du Caire
Les figures n'ont pas encore été transférées de l'ancien site Orange
Le motif est un pentagone ayant ces cinq côtés égaux et deux angles droits, que l'on trouve, au Caire, dans l'art islamique.
À partir d'un segment [AB], tracer sa médiatrice et du milieu I de [AB] dessiner les deux bissectrices faisant des angles de 45° avec cette médiatrice. Le cercle de centre B, passant par A, rencontre une des bissectrices en C et par symétrie le cercle de centre A, passant par B, rencontre l'autre bissectrice en E. La perpendiculaire en C à (BC) coupe la médiatrice en D.
ABCDE est un pentagone semi-régulier : les cinq côtés sont égaux :
en effet, par construction AB = BC = AE. Le quadrilatère IBCD, ayant deux angles droits, est inscriptible dans le cercle de diamètre [BD].
Les angles inscrits CID et CBD sont égaux à 45°, BCD est un triangle rectangle isocèle et BC = CD.
Soit IB = 1, alors BC = CD = 2 et BD = 2 
.
Dans le triangle rectangle IBD, ID2 = BD2 - IB2 = 8 - 1 = 7, d'où ID = 
.
cos(IBD) = 
= 
= 
. IBD = 69,3°, IBC = IBD + 45° = 114,3°,
BDI = 90° - IBD = 20,7°, CDI = 45° + IBD = 65.7°, CDE = 2 CDI = 131.4°.
Deux des angles du pentagone sont droits, deux autres angles mesurent environ 114,3° et le dernier 131,4°, la somme de ces trois angles obtus est de 360° rendant possible l'assemblage de trois pentagones autour des points D et D’ (voir la figure de la macro ci-dessous).
Pour une construction plus efficace du pavé de base avec Cabri, placer deux points A et B. Avec le compas, mesurer la longueur AB et tracer le cercle de centre le milieu I, de rayon 
× AB qui coupe la médiatrice de [AB] en D.
Le triangle BCD étant rectangle isocèle, il suffit de trouver C à l'intersection du cercle de diamètre [BD] et de la médiatrice de [BD]. Le point E est le symétrique de C par rapport à (ID).
Le pentagone ABCDE pave le plan.
Pavé hexagonal formé de quatre pentagones
Pour faciliter le tracé, on pourra tracer un pavé de base hexagonal formé par quatre pentagones.
Pour cela, utiliser la symétrie par rapport à (CD) pour obtenir B’, la symétrie par rapport à (DE) pour obtenir A’ et la symétrie par rapport à (A’B’) pour obtenir le pentagone A”B”C’D’E’.
Créer une macro ayant comme objets initiaux les points A et B et comme objets finaux tous les segments de l'hexagone.
35 pentagones du pavage du Caire
Voir calculs dans : Boule François – Questions sur la géométrie - Nathan pédagogie - 2001, pages 133 et 299
6.b. Pavage de Marjorie Rice
Pavé de basede Marjorie Rice
Voici comment construire son «pavé» :
Sur deux droites perpendiculaires, sécantes en O, placer les points A et B, puis C symétrique de A par rapport à O.
Construire ensuite D, symétrique de B par rapport à C.
Puis on applique au triangle ABD une rotation de centre A qui amène D sur la demi-droite d'origine O contenant B. On note G l'image de D, E l'image de B et F celle de C (F est donc le milieu du segment [EG]).
Le triangle ABD est donc transformé en AEG.
On construit enfin H sur (BG), en projetant E sur (OB).
Pavage du plan de Marjorie Rice
Le pentagone AEFHB pave le plan.
Pour réaliser cette figure utiliser des symétries axiales et des symétries centrales.
Les traces des centres de symétrie situés aux milieux des côtés des pentagones ont été laissées.
6.c. Pavage de Richard E. James
Pavé de Richard James
Voici comment construire son «pavé» :
On dessine tout d'abord deux carrés de même centre, l'un de dimension 2, l'autre de dimension 3.
On place ensuite sur le grand carré quatre points A, B, C et D de telle façon que ABCD soit un carré (de même centre que les deux autres). Chacun des segments AB, BC, CD et DA coupe le petit carré en deux points.
Sur le dessin, la droite (AB) coupe le petit carré en deux points E et F. On a noté O le centre commun des trois carrés. (BC) coupe le petit carré en deux points G et H. (DA) coupe le petit carré en deux points K et L.
On introduit ensuite M, le milieu du segment LE.
Pavage du plan de Richard James
On trace enfin la parallèle à (AM) passant par O et la perpendiculaire à (AM) passant aussi par O.
La première coupe la droite (LE) en un point R. La seconde coupe la droite (FG) en un point S.
Le pentagone OREFS pave le plan.
6.d. Pavage de Rolf Stein
Pavé de Rolf Stein
Construction du «pavé» :
Dans ce qui suit, a représente le nombre 
= 1,13745…
On trace tout d'abord deux demi-droites perpendiculaires de même origine A. Sur l'une, on place B et C de manière que : AB = a et BC = 
.
On construit ensuite D équidistant de A et B avec DA = DB = 1.
Pavage du plan de Rolf Stein
On place ensuite E symétrique de D par rapport à B.
Enfin, sur la demi-droite d'origine C contenant E, on place F de sorte que EF = 2.
Notons G la projection orthogonale de F sur la demi-droite perpendiculaire en A à (AB). On vérifie que FG = 1.
Le pentagone ADEFG pave le plan.
Lycée :
constructions exactes
constructions approchées
Table des matières
Google friendly
Téléchargement
Télécharger pavage.doc : ce document au format « .doc »
Télécharger pavage.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image et une copie
ne devrait pas être référencée comme telle par Google qui considère
l'URL originale comme une erreur de type "soft 404".!
Dans d'autres pages du site
Copyright 2004 - © Patrice Debart
Rétrolien (backlink)
Pavage du plan par Dominique Frin
Page no 77, créée le 26/9/2004
mise à jour le 3/10/2005