Descartes et les Mathématiques

Le plan complexe au bac S

Des carrés ou des triangles autour d'une figure - Études de configurations avec les complexes

Sommaire

1. 3 carrés

2. 2 triangles rectangles isocèles

3. 2 carrés autour d'un triangle rectangle
    bac S national 2005 obligatoire
4. 4 triangles autour d'un quadrilatère
    bac S national 2005 spécialité
    Polynésie 2003 obligatoire

5. Triangles de Napoléon
    bac S Liban 2005 obligatoire
6. Recherche de triangles équilatéraux
    bac S Centres étrangers 1999 obligatoire

Exercices pouvant être démontrés avec des affixes de complexes :

les triangles du BOA

les carrés du BOA

construction du pentagone régulier

théorème de Clifford : cercles

1. Trois carrés

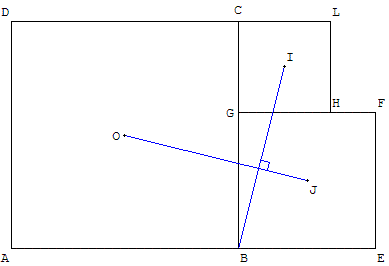
Soit ABCD un carré et G un point de [BC] ; on construit deux carrés extérieurs à ABCD de côtés [BG] et [GC].
On note O, J, I les centres des trois carrés. Montrer que les droites (BI) et (OJ) sont orthogonales et que BI = OJ.

Par dualité (CJ) et (OI) sont orthogonales et CJ = OI.

Solution

On place l'origine en G et l'axe Gx selon (GF).
Les affixes des points sont : G(0), F(a), H(b), C(ib), B(– ia).

On en déduit les affixes des centres, milieux de [CH] et [BF] :
I( b), J( a).

Comme la longueur des côtés de ABCD est a + b, on a :
O(– + i ),
d'où par soustraction l'affixe du vecteur est
( + i ) et ( – i ).

On remarque alors que + i = i ( – i ), d'où l'orthogonalité des vecteurs et l'égalité des longueurs BI et OJ.

Télécharger la figure GéoPlan 3_carre.g2w

2. Deux triangles rectangles isocèles

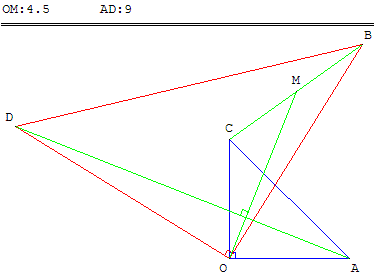
Construction de deux triangles rectangles isocèles directs OAC et OBD autour d'un point O.
On note M est le milieu de [BC]

Montrer que les segments [AD] et [OM] sont perpendiculaires et que AD = 2 OM.

Solution

On place l'origine en O et l'axe Ox selon (OA).
Les affixes sont A(a), B(ia), C(z), D(iz), où a est un réel strictement positif et z un complexe non nul.
M et ont pour affixe , l'affixe de est iz – a = 2i , d'où l'orthogonalité de (OM) et (AD) ainsi que AD = 2 OM.

Télécharger la figure GéoPlan tr_boa_1_bis.g2w

Autre exercice
(AB) perpendiculaire à (CD) et AB = CD : voir les problèmes du BOA

3. Deux carrés autour d'un triangle rectangle

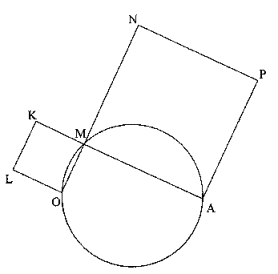
Bac S national 2005 : exercice pour les candidats n'ayant pas suivi l'enseignement de spécialité.

Dans le plan orienté, on considère les points O et A fixés et distincts, le cercle C de diamètre [OA], un point M variable appartenant au cercle C et distinct des points O et A, ainsi que les carrés de sens direct MAPN et MKLO. La figure est représentée ci-dessus.

Le but de l'exercice est de mettre en évidence quelques éléments invariants de la figure et de montrer que le point N appartient à un cercle à déterminer.

On munit le plan complexe d'un repère orthonormal direct de sorte que les affixes des points O et A soient respectivement 0 et 1.

On désigne par i le nombre complexe de module 1 et d'argument . On note k, l, m, n et p les affixes respectives des points K, L, M, N et P.

1) Démontrer que, quel que soit le point M choisi sur le cercle C,
on a = .

2) Établir les relations suivantes : l = i m et p = − im + 1 + i.
On admettra que l'on a également n = (1 – i)m + i et k = (1 + i)m.

3) a) Démontrer que le milieu Ω du segment [PL] est un point indépendant de la position du point M sur le cercle C.
b) Démontrer que le point Ω appartient au cercle C et préciser sa position sur ce cercle.

4) a) Calculer la distance KN et démontrer que cette distance est constante.
b) Quelle est la nature du triangle ΩNK ?

5) Démontrer que le point N appartient à un cercle fixe, indépendant du point M, dont on déterminera le centre et le rayon.

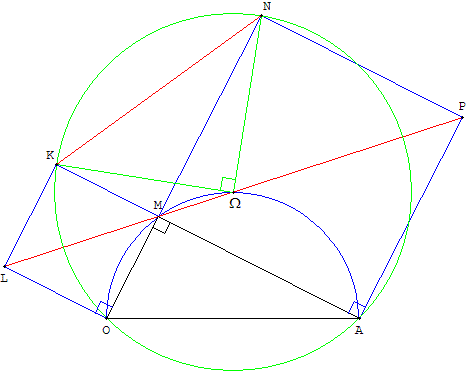
Indications

3) ω = (p + l) = + i.

4) KN = |n–k| = |(1 – i)m + i – (1 + i) m| = |i – 2im| = |– 2i| = 1 = OA.

k – ω = i (n – ω). D'où K est l'image de N par la rotation de centre Ω et d'angle , sens direct. Le triangle ΩNK est rectangle isocèle en Ω.

5) KN = 1 et comme le triangle ΩNK est rectangle isocèle, ΩN² + ΩN² = 2 ΩN² = KN² = 1. N appartient au cercle de centre Ω et de rayon .

Télécharger la figure GéoPlan 2_carre.g2w

Voir : BOA triangle rectangle - Homothéties

Figure de Renan : démonstration du théorème de Pythagore, par la méthode des aires

4. Quatre triangles autour d'un quadrilatère − configuration de Van Aubel

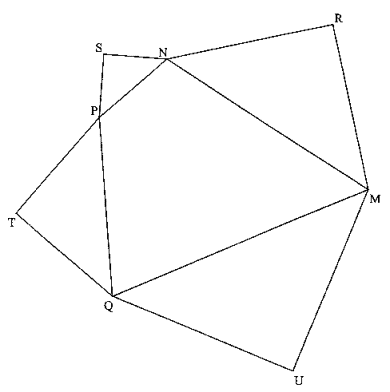
a. Bac S national 2005 : exercice pour les candidats ayant suivi l'enseignement de spécialité.

Le but de l'exercice est d'étudier quelques propriétés de la figure ci-dessus. Cette figure complétée sera à rendre avec la copie.

On munit le plan d'un repère orthonormal direct (O, , ).

Le quadrilatère MNPQ est un quadrilatère non croisé et de sens direct. Les triangles MRN, NSP, PTQ et QUM sont des triangles rectangles isocèles, extérieurs au quadrilatère MNPQ et de sens direct (les sommets des angles droits étant respectivement les points R, S, T et U).

Partie A

On désigne par m, n, p et q, les affixes respectives des points M, N, P et Q.

1) Soit f la similitude directe de centre M qui transforme N en R.

• Déterminer le rapport et l'angle de la similitude f.
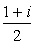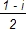• On désigne par r l'affixe du point R. Démontrer que : r = m + n

où i désigne le nombre complexe de module 1 et d'argument (on pourra éventuellement utiliser l'écriture complexe de la similitude f).

On admettra que l'on a également les résultats s = n + p, t = p + q et

u = q + m, où s, t et u désignent les affixes respectives des points S, T et U.

2) Démontrer que les quadruplets (M, N, P, Q) et (R, S, T, U) ont le même isobarycentre.

3) a) Démontrer l'égalité u – s = i (t – r).

b) Que peut-on en déduire pour les longueurs des segments [RT] et [SU], d'une part, et pour les droites (RT) et (SU), d'autre part ?

Partie B

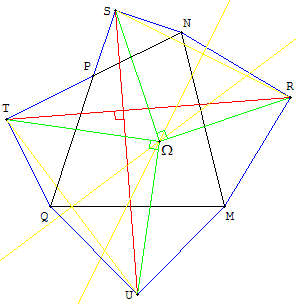
Cette partie sera traitée sans utilisation des nombres complexes.

1) Démontrer, en utilisant les résultats établis dans la partie A, qu'il existe une unique rotation g qui transforme R en S et T en U.

2) Décrire comment construire géométriquement le point Ω, centre de la rotation g. Réaliser cette construction sur la figure.

Indications

1) La similitude f est de rapport et d'angle –. Elle est de la forme z’ = az + b, avec a = – i.

3) RT = SU et les droites (RT) et (SU) sont perpendiculaires.
Le quadrilatère RSTU est un pseudo-carré.

B) La rotation g(Ω, ) transforme R en S et T en U. ΩR = ΩS donc Ω est sur la médiatrice de [RS], Ω est aussi sur la médiatrice de [TU] ; ces deux médiatrices sont sécantes en Ω.

Démonstration avec la rotation, voir : théorème de Van Aubel

Cas particulier lorsque les diagonales de MNPQ sont égales et perpendiculaires, voir : similitude

Télécharger la figure GéoPlan tr_aubel.g2w

4.b. Triangle rectangle isocèle direct

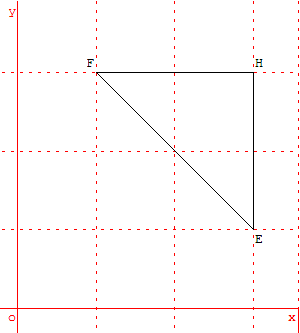
Bac S Polynésie 2003 : exercice pour les candidats n'ayant pas suivi l'enseignement de spécialité.

1. a. Le point E a pour affixe z_E = 3 + i et le point F a pour affixe z_F = 1 + 3i.
Placer les points E et F.
Construire le point H tel que EHF soit un triangle rectangle isocèle direct de sommet H, c'est-à-dire tel que (, ) = .

b. On désigne par z_H l'affixe de H.
Montrer que = 1 et que arg = [2π].
En déduire que z_H = 3 + 3i.

Commentaire acerbe

Quel débauche de moyens pour un résultat à la portée d'un élève de troisième, ce n'est pas avec cette artillerie que l'on motivera nos élèves pour les mathématiques.

Configuration de Van Aubel

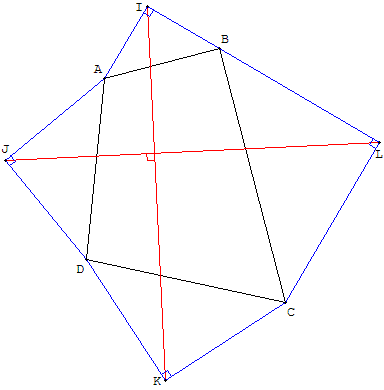
A, B, C et D sont quatre points du plan.

4.b.1. Construire les triangles rectangles isocèles directs BIA, AJD, DKC, et CLB d'angles droits respectifs BIA, AJD, DKC, et CLB.
(ABCD est un quadrilatère convexe indirect et les triangles rectangles isocèles sont à l'extérieur du quadrilatère).

4.b.2. Conjecturer les positions relatives des droites (IK) et (LJ) et le rapport des longueurs des segments [IK] et [LJ].

4.b.3. a. On désigne par a, b et z_I les affixes respectives des points A, B et I.
Montrer que = 1 et que arg = [2π].
En déduire que z_I = .
4.b.3. b. Avec les points B, C et L d'affixes respectives b, c et z_L, exprimer sans démonstration z_L en fonction de b et c.
4.b.3. c. Avec les points C, D et K d'affixes respectives c, d et z_K, exprimer de même z_K en fonction de c et d.
Avec les points D, A et J d'affixes respectives d, a et z_J, exprimer z_J en fonction de d et a.

4.b.3. d. Montrer que z_L – z_J = i(z_K – z_I).
En déduire que les droites (JL) et (IK) sont perpendiculaires et que JL = IK.

Télécharger la figure GéoPlan tr_aubel2.g2w

5. Triangles de Napoléon

Le plan complexe est rapporté à un repère orthonormal direct (O, , ), unité graphique : 0,5cm.

On note j le nombre complexe e^{i 2π/3}.

On considère les points A, B et C d'affixes respectives a = 8, b = 6j et c = 8j².

Soit A’ l'image de B par la rotation de centre C et d'angle .

Soit B’ l'image de C par la rotation de centre A et d'angle .

Soit C’ l'image de A par la rotation de centre B et d'angle .

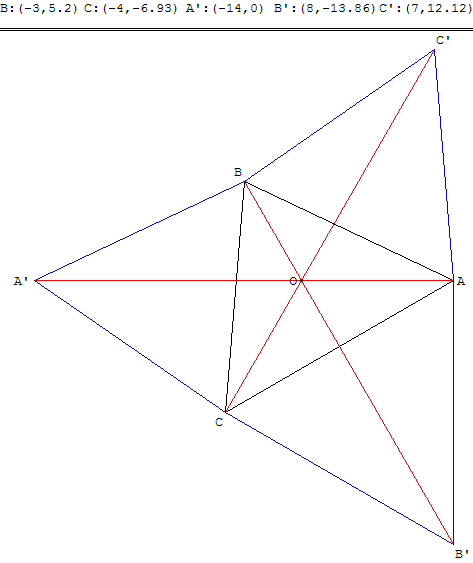
1. Placer les points A, B, C, A’, B’ et C’ dans le repère donné.

2. On appelle a’, b’ et c’ les affixes respectives des points A’, B’ et C’.

• Calculer a’. On vérifiera que a’ est un nombre réel.
• Montrer que b’ = 16e^{− iπ/3}.

En déduire que O est un point de la droite (BB’).

• On admet que c’ = 7 + 7i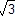. Montrer que les droites (AA’), (BB’) et (CC’) sont concourantes en O.

3. On se propose désormais de montrer que la distance MA + MB + MC est minimale lorsque M = O.

• Calculer la distance OA + OB + OC.
• Montrer que j³ = 1 et que 1 + j + j² = 0.
• On considère un point M quelconque d'affixe z du plan complexe.

On rappelle que a = 8, b = 6j et c = 8j².
Déduire des questions précédentes, les égalités suivantes :
|(a – z) + (b – z)j² + (c – z)j| = |a + bj² + c j| = 22.

• On admet que, quels que soient les nombres complexes z, z’ et z”, on a :

|z + z’ + z”| ≤ |z| + |z’| + |z”|

Montrer que MA + MB + MC est minimale lorsque M = O.

Figure interactive dans GeoGebraTube : point de Fermat

Indications

2. a’ = −14 ; la droite (AA’) est l'axe (Ox) et contient le point O.

b’/b = −8/3 est réel négatif (, ’) = arg(–8/3) = π [2π] : le point O appartient à la droite (BB’).

c’/c = −7/4 le point O appartient à la droite (CC’).

Les droites (AA’), (BB’) et (CC’) sont concourantes en O. O est le point de Torricelli du triangle ABC (dit aussi point de Fermat).

3. OA + OB + OC = 22.
MA + MB + MC = |a – z| + |b – z| + |c – z|
MA + MB + MC = |a – z| + |(b – z)j²| + |(c – z)j|
d'où MA + MB + MC ≥ |(a – z) + (b – z)j² + (c – z)j|
soit MA + MB + MC ≥ 22
d'où MA + MB + MC ≥ OA + OB + OC.

Le point O réalise le minimum de la somme MA + MB + MC lorsque M décrit le plan (Théorème de Torricelli ou de Schruttka).

6. Recherche de triangles équilatéraux

Bac S centres étrangers 1999 : exercice 2, pour les candidats n'ayant que l'enseignement obligatoire

Dans le plan complexe rapporté à un repère orthonormal (O ; , ), A, A’, B, B’ sont les points d'affixes respectives 1, – 1, i, – i.

À tout point M d'affixe z, distinct des points O, A, A’, B et B’, on associe les points M₁ et M₂ d'affixes respectives z₁ et z₂, tels que les triangles BMM₁ et AM₂M soient rectangles et isocèles directs avec

(, ) = (, ) = [2π].

La figure sera complétée et rendue avec la copie.

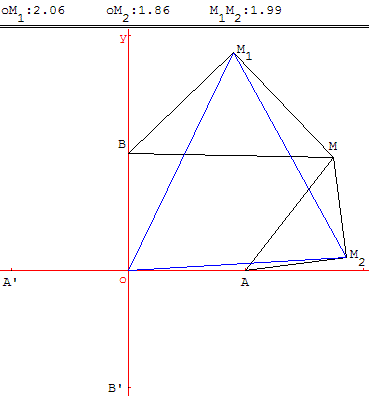
1. a) Justifier les égalités z − z₁ = i(i − z₁) et 1 – z₂ = i(z – z₂).
b) Vérifier que z₁ et z₂ peuvent s'écrire : et

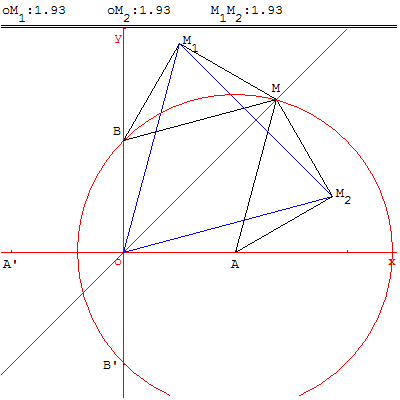
2. On se propose dans cette question de déterminer les points M pour lesquels le triangle OM₁M₂ est équilatéral.

a) Montrer que : OM₁ = OM₂ équivaut à |z + 1| = |z + i|.
En déduire l'ensemble (D) des points M tels que OM₁ = OM₂ et tracer (D) sur la figure.

b) Montrer que : OM₁ = M₁M₂ équivaut à |z + 1|² = 2|z|².
c) En déduire l'ensemble (G) des points M du plan pour lesquels OM₁ = M₁M₂.
On pourra montrer que |z + 1|² = 2|z|² équivaut à |z – 1|² = 2. Tracer (G) sur la figure.

d) En déduire les deux points M pour lesquels OM₁M₂ est un triangle équilatéral et les placer sur la figure.

Télécharger la figure GéoPlan tr_equilateraux.g2w

Table des matières

Dans d'autres pages du site

TS Similitudes

Homothéties

1^ère S Produit scalaire

Mobile friendly

Téléchargement

Télécharger plan_complexe.doc : ce document au format « .doc »

Page n^o 110, créée le 19/5/2007