Descartes et les Mathématiques
Ennéagone régulier
Page en projet : Construction approchée du polygone régulier de 9 côtés.
Sommaire | Ennéagone par Villemin Gerard |
||
Construction du pentagone régulier |
Faire de la | ||
Trisection de l'angle
Partager un angle quelconque en trois angles égaux.
Trouver la trisection d'un angle θ il faut trouver x tel que 3x = θ. On a : cos 3x = 4 cos3x − 3 cos x.
cos x = X est donc solution de l'équation cos θ = 4 X3 − 3 X.
La trisection revient à savoir si les solutions de cette équation sont constructibles.
D'après le théorème de Wantzel, pour que la trisection soit possible, l'équation 4 X3 − 3 X − cos θ = 0 doit être réductible au second degré dans Q.
Par exemple, la trisection d'un angle de mesure θ = 
n'est pas possible :
cos(
), solution de l'équation irréductible dans Q[X] : 4 X3 − 3 X − 
= 0, est algébrique sur Q de degré 3.
Ce qui montre, du même coup, l'impossibilité de tracer à la « règle et au compas » l'ennéagone régulier (9 côtés), résultat prouvé en 1801 par Gauss.
Ennéagone
Côtés |
Angle au |
Angle |
|
Ennéagone |
9 |
40° |
140° |
n côtés |
n |
 |
 |
Non constructible à la « règle et au compas », car la trisection d'un angle de mesure n'est pas possible, résultat prouvé en 1801 par Gauss.
Construction de Thalès
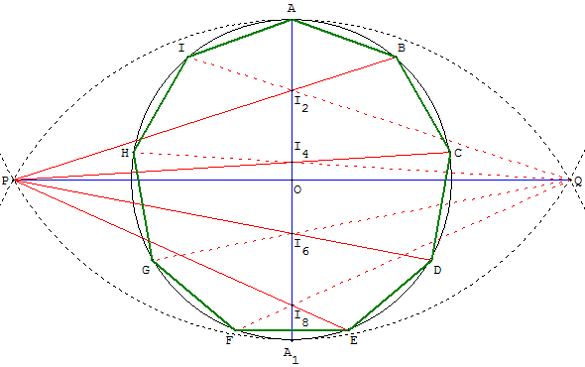
Cette construction d'un ennéagone presque régulier est attribuée au mathématicien et philosophe grec Thalès de Milet (vers 600 avant J.-C.). Elle nécessite la règle et deux ouvertures de compas.
Deux points A et A1 étant donnés, tracer le cercle (c) de diamètre [AA1].
Les cercles de centres A et A1 et de rayon AA1 se coupent en P et Q.
On divise le diamètre [AA1] en n = 9 parties égales.
Les droites (PI2), (PI4), (PI6) et (PI8) rencontrent
le cercle (c) en B, C, D et E, sommets du polygone.
On le complète par symétrie par rapport à (AA1).
On obtient alors les points I, H, G et F intersections du cercle (c) et des droites (QI2), (QI4), (QI6) et (QI8).
ABCDEFGHI est une construction approchée de l'ennéagone régulier.
Copyright 2013 - © Patrice Debart
Construction par neusis
Une construction par neusis ou par inclinaison est un procédé de construction utilisant une règle graduée et consistant à tracer un segment de longueur donnée dont les extrémités se trouvent sur deux courbes données. Il s'agit ici de construire un angle de 140°…
Partager un cercle en 9
Tracer un ennéagone régulier, non constructible à la « règle et au compas »,
|
|
Page créée le 30/12/2010 |